神经网络前向微分和后向微分区别
1. 计算顺序
-
前向微分(前向模式)
-
从输入到输出逐层计算:沿计算图的正向顺序(输入层 → 输出层),同时计算函数值和导数。
-
每一步同步更新导数:每个中间变量的导数随值一起计算,例如,对输入变量 x 的导数逐层传递。
-
-
后向微分(反向模式)
-
先完成前向计算,再反向传播导数:
-
前向过程:计算所有中间变量的值(输入层 → 输出层)。
-
反向过程:从输出层开始,按链式法则反向计算梯度(输出层 → 输入层)。
-
-
2. 计算复杂度
-
前向微分
-
计算单个输入的导数效率高,但输入多时效率低。
-
若输入有 n 个变量,需运行 n 次前向模式才能得到全部梯度。
-
适用场景:输入维度低(如 n 小)、输出维度高(如 m 大)。
-
-
后向微分
-
一次反向传播即可计算所有输入的导数,输入多时效率高。
-
若输出是标量(如神经网络的损失函数),仅需一次反向传播即可获得全部参数的梯度。
-
适用场景:输出维度低(如标量)、输入维度高(如神经网络参数数量大)。
-
3. 在神经网络中的应用
-
前向微分
-
较少用于神经网络训练,因为网络参数通常数量庞大(输入维度高),多次前向计算代价过高。
-
可能在特定场景使用,如实时计算单个参数的敏感度。
-
-
后向微分
-
反向传播(Backpropagation)是反向模式的具体实现,是神经网络训练的基石。
-
高效计算损失函数对百万级参数的梯度,支撑梯度下降优化。
-
4. 内存与实现
-
前向微分
-
内存占用低:仅需保存当前变量的值和导数,无需存储整个计算图。
-
实现简单,适合嵌入式系统等资源受限场景。
-
-
后向微分
-
内存占用高:需存储前向过程的所有中间变量,以便反向计算梯度。
-
实现复杂,依赖计算图构建和动态跟踪(如 PyTorch 的 Autograd)。
-
5. 示例对比


相关文章:

神经网络前向微分和后向微分区别
1. 计算顺序 前向微分(前向模式) 从输入到输出逐层计算:沿计算图的正向顺序(输入层 → 输出层),同时计算函数值和导数。 每一步同步更新导数:每个中间变量的导数随值一起计算,例如&…...

Android 创建一个全局通用的ViewModel
(推荐)使用ViewModelStore 代码示例: class MyApplication : Application(), ViewModelStoreOwner {private val mViewModelStore ViewModelStore()override fun onCreate() {super.onCreate()}override val viewModelStore: ViewModelSto…...

windows 利用nvm 管理node.js 2025最新版
1.首先在下载nvm 下载链接 2. 下载最新版本的nvm 3. 同意协议 注意:选择安装路径 之后一直下一步即可 可以取消勾选 open with Powershell 勾选后它会自动打开Powershell 这里选用cmd 输入以下命令查看是否安装成功 nvm version 查看已经安装的版本 我之前自…...

基于物联网技术的电动车防盗系统设计(论文+源码)
1总体设计 本课题为基于物联网技术的电动车防盗系统,在此将整个系统架构设计如图2.1所示,其采用STM32F103单片机为控制器,通过NEO-6M实现GPS定位功能,通过红外传感器检测电瓶是否离开位,通过Air202 NBIOT模块将当前的数…...
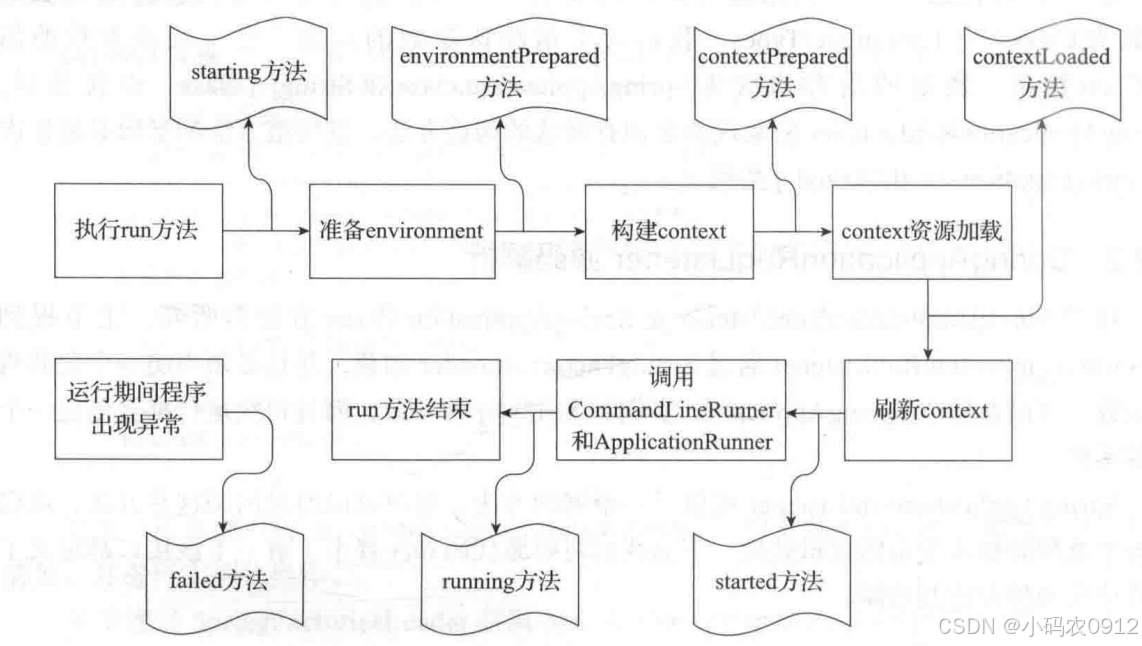
run方法执行过程分析
文章目录 run方法核心流程SpringApplicationRunListener监听器监听器的配置与加载SpringApplicationRunListener源码解析实现类EventPublishingRunListener 初始化ApplicationArguments初始化ConfigurableEnvironment获取或创建环境配置环境 打印BannerSpring应用上下文的创建S…...

关联封号率降70%!2025最新IP隔离方案实操手册
高效运营安全防护,跨境卖家必看的风险规避指南 跨境账号管理的核心挑战:关联封号风险激增 2024年,随着全球电商平台对账号合规的审查日益严苛,“关联封号”已成为跨境卖家最头疼的问题之一。无论是同一IP登录多账号、员工操作失误…...

LeetCode 解题思路 10(Hot 100)
解题思路: 上边: 从左到右遍历顶行,完成后上边界下移(top)。右边: 从上到下遍历右列,完成后右边界左移(right–)。下边: 从右到左遍历底行,完成后…...
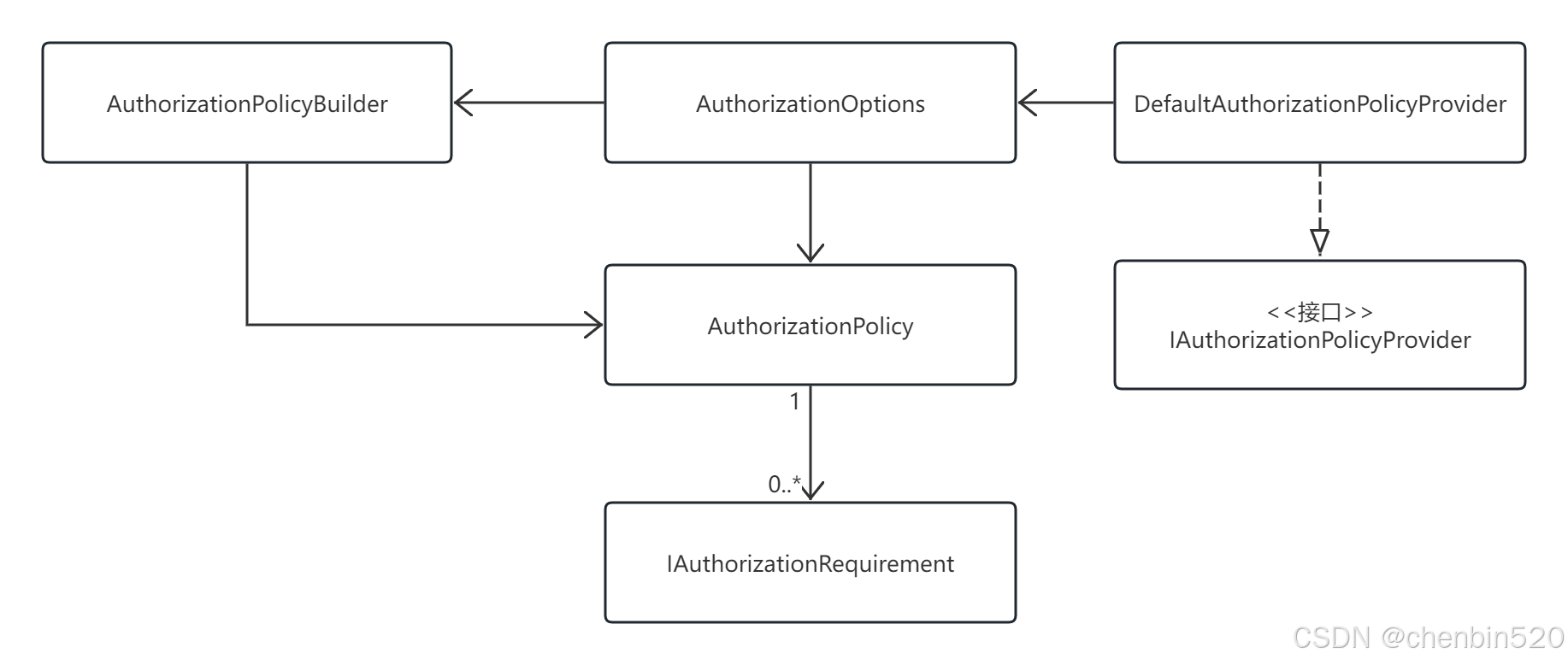
ASP.NET Core JWT认证与授权
1.JWT结构 JSON Web Token(JWT)是一种用于在网络应用之间安全传输声明的开放标准(RFC 7519)。它通常由三部分组成,以紧凑的字符串形式表示,在身份验证、信息交换等场景中广泛应用。 2.JWT权限认证 2.1添…...
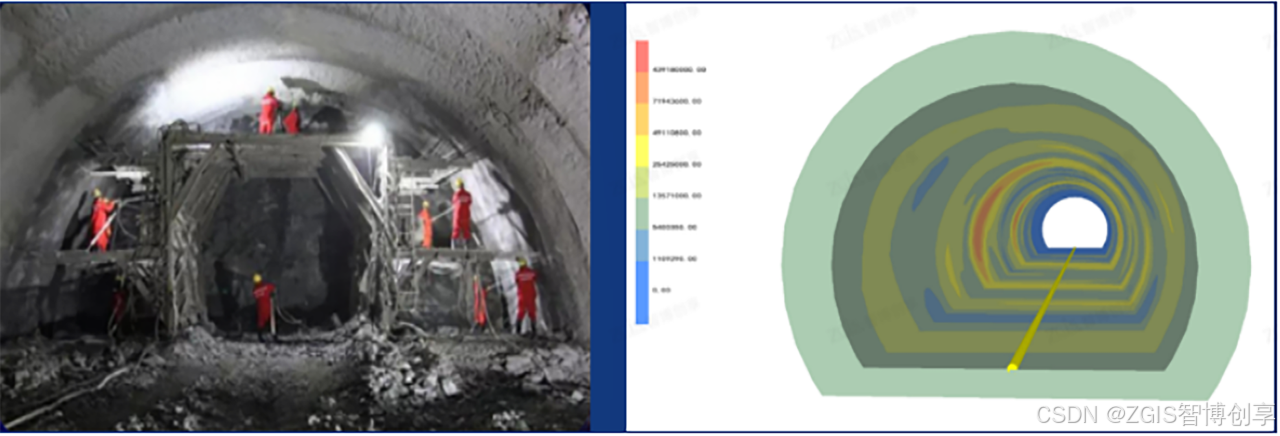
城市地质安全专题连载⑧ | 强化工程地质安全保障力度,为工程项目全栈护航
作者 | 徐海洋、孙美琴 在城市化进程日益加速的今天,城市地质安全问题日益凸显,成为制约城市可持续发展的关键因素之一。从隧道掘进中的突发灾害,到高层建筑地基的稳定性挑战,再到城市地下空间的开发利用风险,地质安全…...

50.xilinx fir滤波器系数重加载如何控制
, 注意:matlab量化后的滤波器系数为有符号数,它是以补码形式存储的,手动计算验证时注意转换为负数对应数值进行计算。...

低代码平台的后端架构设计与核心技术解析
引言:低代码如何颠覆传统后端开发? 在传统开发模式下,一个简单用户管理系统的后端开发需要: 3天数据库设计5天REST API开发2天权限模块对接50个易出错的代码文件 而现代低代码平台通过可视化建模自动化生成,可将开发…...
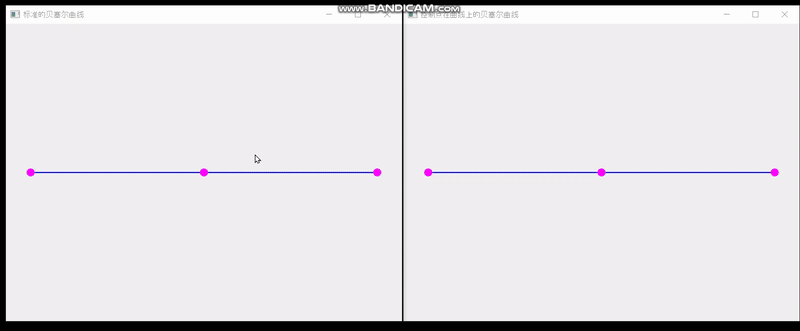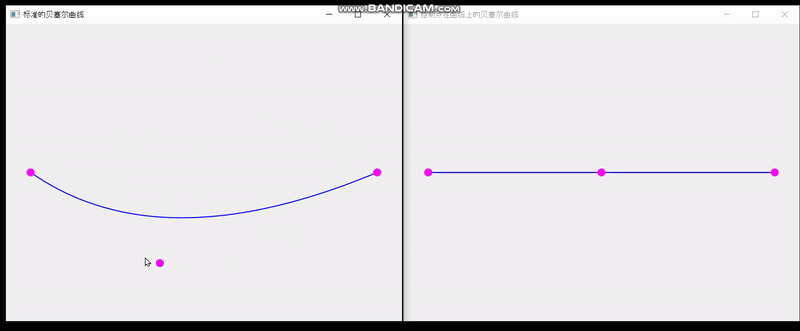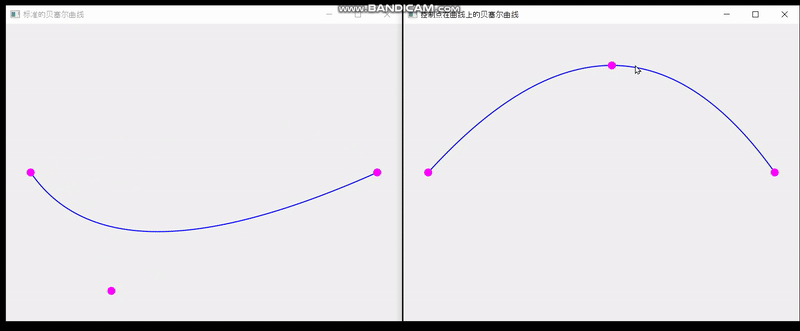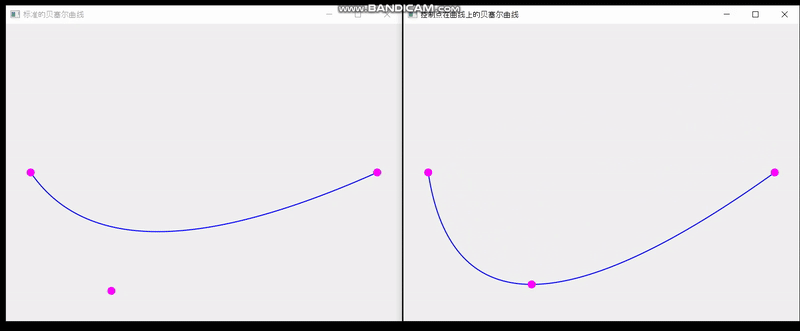
QT实现单个控制点在曲线上的贝塞尔曲线
最终效果: 一共三个文件 main.cpp #include <QApplication> #include "SplineBoard.h" int main(int argc,char** argv) {QApplication a(argc, argv);SplineBoard b;b.setWindowTitle("标准的贝塞尔曲线");b.show();SplineBoard b2(0.0001);b2.sh…...

svn 通过127.0.01能访问 但通过公网IP不能访问,这是什么原因?
连接失败的提示如下 1、SVN的启动方法 方法一: svnserve -d -r /mnt/svn 方法二: svnserve -d --listen-port 3690 -r /mnt/svn 方法三: svnserve -d -r /mnt/svn --listen-host 0.0.0.0 2、首先检查svn服务器是否启动 方法一&#x…...
)
学习DeepSeek V3 与 R1 核心区别(按功能维度分类)
一、定位与架构 V3(通用型模型) 定位:多模态通用大模型,擅长文本生成、多语言翻译、智能客服等多样化任务12。架构:混合专家(MoE)架构,总参数 6710 亿,每次…...

C++中的 互斥量
1.概念: 为什么:线程的异步性,不是按照时间来的!!! C并发以及多线程的秘密-CSDN博客 目的 多线程编程中,当多个线程可能同时访问和修改共享资源时,会导致数据不一致或程序错误。…...
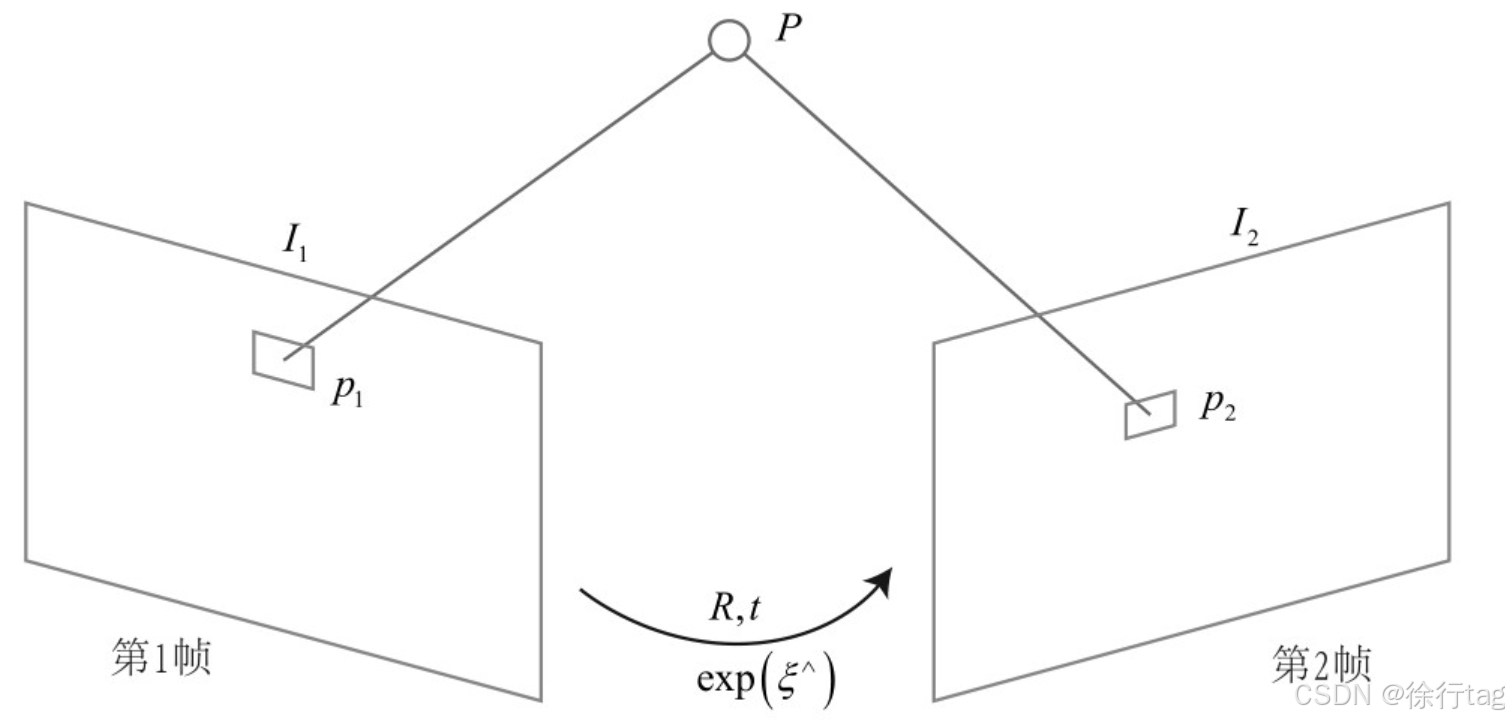
直接法估计相机位姿
引入 在前面的文章:运动跟踪——Lucas-Kanade光流中,我们了解到特征点法存在一些缺陷,并且用光流法追踪像素点的运动来替代特征点法进行特征点匹配的过程来解决这些缺陷。而这篇文章要介绍的直接法则是通过计算特征点在下一时刻图像中的位置…...

PHP动态网站建设
如何配置虚拟主机 1. 学习提纲 本地发布与互联网发布:介绍了如何通过本地IP地址和互联网域名发布网站。 虚拟主机配置与访问:讲解了如何配置虚拟主机,并通过自定义域名访问不同的站点目录。 Web服务器配置:详细说明了如何配置A…...

【gRPC】Java高性能远程调用之gRPC详解
gRPC详解 一、什么是gRPC?二、用proto生成代码2.1、前期准备2.2、protobuf插件安装 三、简单 RPC3.1、开发gRPC服务端3.2、开发gRPC客户端3.3、验证gRPC服务 四、服务器端流式 RPC4.1、开发一个gRPC服务,类型是服务端流4.2、开发一个客户端,调…...

数据结构知识学习小结
一、动态内存分配基本步骤 1、内存分配简单示例: 个人对于示例的理解: 定义一个整型的指针变量p(着重认为它是一个“变量”我觉得可能会更好理解),这个变量用来存地址的,而不是“值”,malloc函…...

分布式锁—2.Redisson的可重入锁一
大纲 1.Redisson可重入锁RedissonLock概述 2.可重入锁源码之创建RedissonClient实例 3.可重入锁源码之lua脚本加锁逻辑 4.可重入锁源码之WatchDog维持加锁逻辑 5.可重入锁源码之可重入加锁逻辑 6.可重入锁源码之锁的互斥阻塞逻辑 7.可重入锁源码之释放锁逻辑 8.可重入锁…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
