[Lc(2)滑动窗口_1] 长度最小的数组 | 无重复字符的最长子串 | 最大连续1的个数 III | 将 x 减到 0 的最小操作数
目录
1. 长度最小的字数组
题解
代码
⭕2.无重复字符的最长子串
题解
代码
3.最大连续1的个数 III
题解
代码
4.将 x 减到 0 的最小操作数
题解
代码

1. 长度最小的字数组
题目链接:209.长度最小的字数组
题目分析:
给定一个含有 n 个 正整数 的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
(子数组:是连续的!!!)
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4]
输出:1题解
- 注意题目说的是 正整数 数组,说明数组里面的数是大于等于0的数。
- 因此这道题我们有一种优化的方法。
- 题目让找连续的子数组和>=target,并且长度最小。有很多种情况,但是我们选择的是 最小长度。

算法原理:
不管什么题,首先我们一定会先想到的是 暴力求解,因为只有暴力求解出来了,我们就可以在暴力求解的基础上进行优化~
解法一:暴力枚举出所有的子数组的和
两层for循环,O(N^2)
for(int i=0;i<n;i++)for(int j=i;j<n;j++)sum+=num[j];
//固定一个数,挨个往后加if(sum>=target)min(len,j-i+1)注意到此时暴力枚举是有优化的。
题目说的是一个 正整数数组,都是大于等于0的数,这个 sum是呈现出递增的状态的,单调递增!
在暴力求解中,此时right还要++,但是注意题目本来要求的就是 最小长度
此时sum在加上往上走了一步的right的num[right],一定是满足sum>=target,但是len变成5了,一定不会是最终结果
因此当条件已经满足sum>=target ,right就不用动了。right后面也就不用再枚举了。

那现在让 left+1,right和left指向同一下标,然后再重复上面过程,那有个问题,这段区间的和能不能直接算出来?
- 当然可以。
- 现在sum=8,我只需要把让sum减去num[left],不就是现在left和right所在的区间和算出来吗。
- 没有必要让right傻傻的回退然后重新加。因此right不动,更新sum=6.

因此我们从暴力枚举中发现两个优化:
- 一个是right 满足后,后面不用枚举
- 一个left++,right不用回退,
所以我们可以利用单调性,使用双指针优化。
解法二:利用单调性,使用 “同向双指针” 来优化
当我们在暴力枚举的策略中发现left和right都是从左向右一个方向移动,我们就称为这两个指针叫做同向指针。同向双指针又称为滑动窗口。
什么是滑动窗口?
本质上是 “同向双指针”,left从左到右移动,right不回退,从左到右移动,用left和right一直 维护这个区间的和,然后这两个指针从左向右移动的过程非常像一个窗口在这个数组里滑来滑去。

什么时候用滑动窗口?
利用单调性,用滑动窗口解决问题。
当我们发现在暴力求解时,两个指针都可以做到 不回退,都是向同一个方向移动的时候,此时就可以用滑动窗口。
滑动窗口怎么用?
- 初始left=0,right=0,充当窗口左端点,右端点。用left,right标记窗口左区间,右区间。
- 右窗口(++right)(右值进窗口)
- 判断
-
- 根据判断决定是否 左窗口(++left)(左值出窗口)
- 更新结果
-
- 2,3都有可能会更新结果,看题目要求
左窗口,判断,右窗口一直循环,直到right 超过区间长度结束,更新结果看题目要求(右窗口,左窗口都有可能),。

滑动窗口正确性
- 暴力枚举肯定对的,因为已经把所有子数组的情况都找出来了。
- 虽然滑动窗口并没有把没有把所有情况都枚举出来,但是这里利用单调性,规避了没有必要的枚举
- 虽然没有把所有情况真正枚举出来,但是已经判断出有些子数组不是最终结果,已经把所有结果都考虑进来了,所以这种策略是跟暴力枚举是一样正确的。
滑动窗口时间复杂度
进窗口是一个循环,判断也是一个循环。
两层循环套在一起。可能会觉得时间复杂度O(N^2),但是不能看代码算时间复杂度,要看实际情况分析实际复杂度。
实际我们只会让right向前移动,left也向前移动,即使时最坏情况,right移动到最后一个元素,left 也移动到最后一个元素,因为单调性,总共也就操作了 n+n=2n 次 整体时间复杂度O(N)。

代码

要考虑到,栈溢出(heap-buffer-overflow) 的边界情况

可详见前文
在Leetcode中,无穷大和无穷小分别怎么表示
C/C++中可以使用INT_MAX和INT_MIN
⭕2.无重复字符的最长子串
题目链接:3. 无重复字符的最长子串
题目分析:
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。子串和子数组都是连续的
❗❗❗ 模拟分析示例:

题解
算法原理:
首先还是暴力枚举,然后根据暴力枚举进行优化。
- 以下面为例,两层for循环,但是下面找到的结果都是我们站在上帝角度,编译器并不知到什么时候结束。
- 一般对应判断是否有重复元素,我们都可以用哈希表来解决问题。
- 使用哈希表,判断是否有重复元素,比如让你判断一个数组是否有重复,或者两个数组是否有重复都可以用哈希映射!

解法一:暴力枚举+哈希表(判断字符是否重复出现)
O(N^2)
根据解法一做优化,定义一个left,right指针。当right走到有重复的元素后,已经找到一个字串,其中left到right区间每个元素都已经进入hash表。

此时left向前走一步,但是这个区间还是有重复元素,因此left要走到没有重复的区间才行,

然后这个时候以前做法是right回退然后重新往下走,但是这里left到right区间元素本来就在hash表里
因此就不需要right回退了,而是向right继续向前走。然后重复上面过程,直到right走到结尾。结束~

这不就是滑动窗口的思想吗。双向指针,left往前走,right不回退一直往前走
解法二:利用规律,使用 “滑动窗口” 解决问题
- left=0,right=0
- 进窗口
- 判断
-
- 出窗口
- 更新结果
进窗口、判断、出窗口,更新结果是一个大循环过程。直到right到结尾循环结束。
其中判断、出窗口是一个小循环(直到跳出重复字符)。不过时间复杂度还是O(N).
注意:
- 更新结果可能在 进窗口后,判断后,出窗口后,判断后任意一个地方,看题目要求
本题:
- 进窗口 ->-> 让字符进入哈希表
- 判断-> 窗口内出现重复元素
- 出窗口-> 从哈希表中删除该字符
代码
class Solution {
public:int lengthOfLongestSubstring(string s) {//!!if(s.empty()) return 0; // 处理空输入vector<char> str;for(char c:s) str.push_back(c);int left=0,right=0,n=str.size(),len=0;//unordered_set ret;unordered_set<char> ret;while(right<n){
//先检查while(ret.count(str[right])){ret.erase(str[left]);left++;//利用了连续性//表中 发现了右元素已存在//要在左边 进行跳过}
//不存在 就插入ret.insert(str[right]);len=max(len,right-left+1);right++;}return len;}
};总结一下:
利用单调性,使用 双指针 解决问题。
- 一般left和right,一个指向数组最左边,一个指向数组最右边,然后一次可以排除一批,再然后left++,–right,两个指针是对撞的。
这里利用单调性或者利用规律,使用 滑动窗口 解决问题
- 滑动窗口也使用双指针解决问题,不过left一直从前往后走,right不回退从前往后走,两个指针是同向的。因此滑动窗口本质其实是 同向双指针。
3.最大连续1的个数 III
题目链接:1004. 最大连续1的个数 III
题目分析:
给定一个二进制数组 nums 和一个整数 k,假设最多可以翻转 k 个 0 ,则返回执行操作后 数组中连续 1 的最大个数 。
示例 1:
输入:nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出:6
解释:[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 6。示例 2:
输入:nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出:10
解释:[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 10。题解
题目说的翻转实际上是把0变成1的意思,最多翻转K次,说明小于等于K都是可以的。

拿到题我们开始肯定想的是暴力求解。
如果直接暴力求解,遇到0->1了,那下一次在遍历就有问题了。
因此我们换一个思路。这道题不是让转化后最大连续1的个数吗。
我们转化为:找出最长的子数组,数组里0的个数不超过K个,这个数组里面0一定能够转化成1。
算法原理:
解法一:暴力枚举+zero计数器
伪代码,两层for循环,统计zero的个数,满足zero>k,统计此时数组长度,然后重新进入循环,注意每次zero都清0
for(int i=0;i<n;++i)for(int j=i;j<n;++j)//双指针 查找出一段区间if(nums[j]==0)++zero;if(zero>k)ret=max(ret,right-left+1)然后我们根据暴力枚举,看看有没有优化的可能。
定义两个指针left,right,right走到zero>k的位置,zero=3,大于k。

按照暴力求解left++,然后right回溯然后重新往后走。但是我们发现没有必要,现在left往前走一步,你会发现,right还是停留在老位置,这个区间不用在管的,直接丢弃。

因此,让left一直走到zero<=k的位置。然后 right也根本不用回溯 然后在重新走,而是直接往后走就行了。

根据上面的发现,当在暴力枚举中,发现left,right是同向移动的,利用这个规律,使用滑动窗口解决问题
解法二:利用规律,使用滑动窗口
- left=0,right=0
- 进窗口
- 判断
-
- 出窗口
- 更新结果
进窗口 -> 如果是1,不理会。如果是0,计数器+1
判断 -> zero>k
出窗口 -> 如果是1,不理会。如果是0,计数器-1
更新结果:在判断之后在更新
代码
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int left = 0, right = 0, zero = 0;int n = nums.size(), len = 0;while (right < n) {//进 窗口if (nums[right] == 0)zero++;while (zero > k) {//循环判断if (nums[left] == 0)zero--;left++;}len = max(len, right - left + 1);right++;}return len;}
};4.将 x 减到 0 的最小操作数
题目链接:1658. 将 x 减到 0 的最小操作数
题目分析:
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。
如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。
示例 1:
输入:nums = [1,1,4,2,3], x = 5
输出:2
解释:最佳解决方案是移除后两个元素,将 x 减到 0 。示例 2:
输入:nums = [5,6,7,8,9], x = 4
输出:-1示例 3:
输入:nums = [3,2,20,1,1,3], x = 10
输出:5
解释:最佳解决方案是移除后三个元素和前两个元素(总共 5 次操作),将 x 减到 0 。题解
这道题让每次从数组左右两边移除一个数,然后就是一个新的数组,然后再从新的数组再从左右两边移除一个数。
- 但是如果真的硬着头皮开始做,其实是很困难的。
- 并不知道每次是从最左边走还是最右边找。有可能这次左边下次右边或者还是左边,情况太复杂了。

因此我们可以利用 正难则反 的思想
- 正对面解题太难,那就想对立面,换个思路。
- 不是每次从左右两端找一个数吗,那可能找到情况就是a+b=x,a、b什么情况都要,但是中间这个连续区间的和不也是确定的吗sum-x
- 也就是这道题我们转换成,找出最长的子数组长度,所有元素的和正好等于sum-x,然后数组总长减去这段子区间长度不就是问题答案吗
- 如果没找到说明这个数组不存在将x减到0的数,直接返回-1

解法一:暴力求解
初始left,right指向同一下标,当right走到和大于target的时候,left往前走
按照暴力求解,right要回到和left相同下标,然后right在重新往前走,直到再次走到和大于target的地方停下来,然后重复上面过程。

- 但是今天这里不需要right回溯,因为right回溯后重新走到下面的位置,因为left已经往前走了,这段区间的和肯定是更小了
- 因此就不需要right回溯了。要么right不动,要么right往后走。
- 同向双指针 ----> 本质就是滑动窗口
解法二:使用滑动窗口
代码
class Solution {
public:
int minOperations(vector<int>& nums, int x)
{if(nums.empty()) return -1;int sum=0;for(auto c:nums)sum+=c;// 新增边界条件处理if (sum == x) return nums.size(); // 整个数组和正好等于xif (sum < x) return -1; // 总和不足,无法达成目标int target=sum-x,len=0;int left=0,right=0,n=nums.size(),add=0;while(right<n){add+=nums[right];while(add>target){add-=nums[left];left++;}if(add==target)len=max(len,right-left+1);right++;}//!!!len>0 return (len > 0) ? (nums.size() - len) : -1;
}
};测试样例跑不全时,要注意对 边界情况 的处理

- 若不存在这样的子数组(
len = 0)
相关文章:

[Lc(2)滑动窗口_1] 长度最小的数组 | 无重复字符的最长子串 | 最大连续1的个数 III | 将 x 减到 0 的最小操作数
目录 1. 长度最小的字数组 题解 代码 ⭕2.无重复字符的最长子串 题解 代码 3.最大连续1的个数 III 题解 代码 4.将 x 减到 0 的最小操作数 题解 代码 1. 长度最小的字数组 题目链接:209.长度最小的字数组 题目分析: 给定一个含有 n 个 正整数 的数组…...

迷你世界脚本玩家接口:Player
玩家接口:Player 彼得兔 更新时间: 2024-07-28 17:49:05 继承自 Actor 具体函数名及描述如下: 序号 函数名 函数描述 1 getAttr(...) 玩家属性获取 2 setAttr(...) 玩家属性设置 3 getHostUin(...) 获取房主uin 4 isMainPlayer(...) …...

三、0-1搭建springboot+vue3前后端分离-springboot整合mybatis plus 之本地安装mysql
一、安装mysql: 官网下载:https://dev.mysql.com/downloads/mysql/?spm5176.28103460.0.0.40f75d27Stx4Xj 网盘分享:http://链接: https://pan.baidu.com/s/1mS_-VxrKAeRL3utBvD64gg?pwd6666 提取码: 6666 复制这段内容后打开百度网盘手机…...

市场趋势解析与交易策略优化
市场趋势解析与交易策略优化 在市场环境不断变化的情况下,理解市场趋势并优化交易策略是交易者稳健发展的关键。通过科学的方法识别市场动向,结合数据分析优化交易方案,可以提高交易效率并降低风险。本文将探讨趋势分析的要点,并介…...

Spring Boot 常用注解全解析:从核心到进阶的实践指南
目录 引言:为什么注解是Spring Boot开发者的“战略武器”? 一、核心启动注解 1.1 应用启动三剑客 二、Web开发注解 2.1 控制器层注解 三、依赖注入注解 3.1 依赖管理矩阵 四、数据访问注解 4.1 JPA核心注解 五、配置管理注解 5.1 配置绑定注解…...

如何优化FFmpeg拉流性能及避坑指南
FFmpeg作为流媒体处理的核心工具,其拉流性能直接影响直播/点播体验。本文从协议优化、硬件加速、网络策略三大维度切入,结合实战案例与高频踩坑点,助你突破性能瓶颈! 一、性能优化进阶:从协议到硬件的全链路调优 协议选…...

基础dp——动态规划
目录 一、什么是动态规划? 二、动态规划的使用步骤 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值 三、试题讲解 1.最小花费爬楼梯 2.下降路径最小和 3.解码方法 一、什么是动态规划? 动态规划(Dynamic Programming&…...

通过微步API接口对单个IP进行查询
import requests import json# 微步API的URL和你的API密钥 API_URL "https://api.threatbook.cn/v3/ip/query" API_KEY "***" # 替换为你的微步API密钥 def query_threatbook(ip):"""查询微步API接口,判断IP是否为可疑"…...

LLM实践——DeepSeek技术报告学习(含实现逻辑梳理)
目录 一些基本概念:deepseek-r1-zerodeepseek-R1deepseek-R1 distill model: DeepSeek官网:https://www.deepseek.com/ 一些基本概念: post-training:旨在优化预训练模型的特定能力,包括任务适配性、安…...

Autojs无线连接vscode方法
1.获得电脑的IP 在电脑的CMD界面输入 ipconfig 然后找到ipv4的那一行,后面的即是你的电脑IP地址 2.打开vscode的autojs服务 安装autojs插件 在vscode界面按下ctrlshiftp 输入autojs 找到 点击 之后打开手机上的autojs 之后输入刚刚电脑上的地址 可以看到vsc…...

第一节:基于Winform框架的串口助手小项目---基础控件使用《C#编程》
本人于2025年3月2号学习C#编程,要学会一门编程语言,一定要有一个或多个项目的经验才能对着这门语言有深入的了解,为了深入了解和记录学习C#的学习过程,此文章作为足迹以此记录,为后期巩固学习以及参考奠定基础。内容涉…...

小红书湖仓架构的跃迁之路
作者:李鹏霖(丁典),小红书-研发工程师,StarRocks Contributor & Apache Impala Committer 本文整理自小红书工程师在 StarRocks 年度峰会上的分享,介绍了小红书自助分析平台中,StarRocks 与 Iceberg 结合后&#x…...

pytorch高可用的设计策略和集成放大各自功能
在使用 PyTorch 编写模型时,为确保模型具备高可用性,可从模型设计、代码质量、训练过程、部署等多个方面采取相应的方法,以下为你详细介绍: 模型设计层面 模块化设计 实现方式:将模型拆分成多个小的、独立的模块,每个模块负责特定的功能。例如,在一个图像分类模型中,可…...

神经网络前向微分和后向微分区别
1. 计算顺序 前向微分(前向模式) 从输入到输出逐层计算:沿计算图的正向顺序(输入层 → 输出层),同时计算函数值和导数。 每一步同步更新导数:每个中间变量的导数随值一起计算,例如&…...

Android 创建一个全局通用的ViewModel
(推荐)使用ViewModelStore 代码示例: class MyApplication : Application(), ViewModelStoreOwner {private val mViewModelStore ViewModelStore()override fun onCreate() {super.onCreate()}override val viewModelStore: ViewModelSto…...

windows 利用nvm 管理node.js 2025最新版
1.首先在下载nvm 下载链接 2. 下载最新版本的nvm 3. 同意协议 注意:选择安装路径 之后一直下一步即可 可以取消勾选 open with Powershell 勾选后它会自动打开Powershell 这里选用cmd 输入以下命令查看是否安装成功 nvm version 查看已经安装的版本 我之前自…...

基于物联网技术的电动车防盗系统设计(论文+源码)
1总体设计 本课题为基于物联网技术的电动车防盗系统,在此将整个系统架构设计如图2.1所示,其采用STM32F103单片机为控制器,通过NEO-6M实现GPS定位功能,通过红外传感器检测电瓶是否离开位,通过Air202 NBIOT模块将当前的数…...
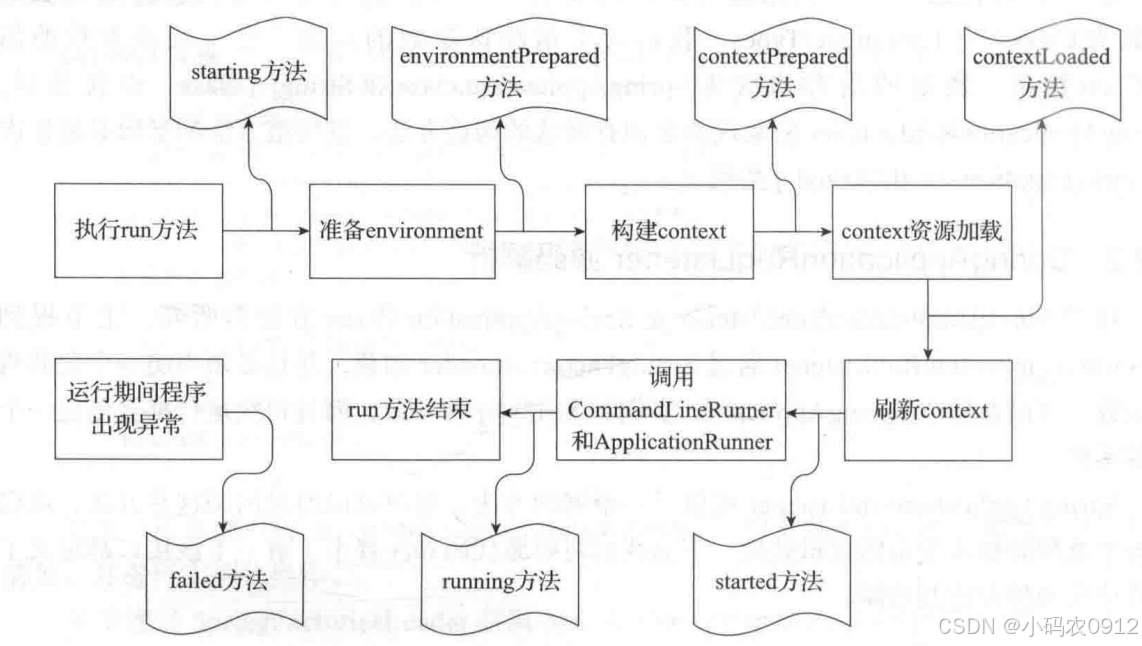
run方法执行过程分析
文章目录 run方法核心流程SpringApplicationRunListener监听器监听器的配置与加载SpringApplicationRunListener源码解析实现类EventPublishingRunListener 初始化ApplicationArguments初始化ConfigurableEnvironment获取或创建环境配置环境 打印BannerSpring应用上下文的创建S…...

关联封号率降70%!2025最新IP隔离方案实操手册
高效运营安全防护,跨境卖家必看的风险规避指南 跨境账号管理的核心挑战:关联封号风险激增 2024年,随着全球电商平台对账号合规的审查日益严苛,“关联封号”已成为跨境卖家最头疼的问题之一。无论是同一IP登录多账号、员工操作失误…...

LeetCode 解题思路 10(Hot 100)
解题思路: 上边: 从左到右遍历顶行,完成后上边界下移(top)。右边: 从上到下遍历右列,完成后右边界左移(right–)。下边: 从右到左遍历底行,完成后…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
