2025-03-08 学习记录--C/C++-C 语言 判断一个数是否是完全平方数
C 语言 判断一个数是否是完全平方数
使用
sqrt函数计算平方根,然后判断平方根的整数部分是否与原数相等。

#include <stdio.h>
#include <math.h>int isPerfectSquare(int num) {if (num < 0) {return 0; // 负数不是完全平方数}int sqrtNum = (int)sqrt(num); // 计算平方根并取整return (sqrtNum * sqrtNum == num); // 判断平方根的平方是否等于原数
}int main() {int num;printf("Enter a number: ");scanf("%d", &num);if (isPerfectSquare(num)) {printf("%d is a perfect square.\n", num);} else {printf("%d is not a perfect square.\n", num);}return 0;
}


相关文章:

2025-03-08 学习记录--C/C++-C 语言 判断一个数是否是完全平方数
C 语言 判断一个数是否是完全平方数 使用 sqrt 函数计算平方根,然后判断平方根的整数部分是否与原数相等。 #include <stdio.h> #include <math.h>int isPerfectSquare(int num) {if (num < 0) {return 0; // 负数不是完全平方数}int sqrtNum (int)…...

八、排序算法
一些简单的排序算法 8.1 冒泡排序 void Bubble_sort(int a[] , int len){int i,j,flag,tmp;for(i=0 ; i < len-1 ; i++){flag = 1;for(j=0 ; j < len-1-i ; j++){if(a[j] > a[j+1]){tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;flag = 0;}}if(flag == 1){break;}}…...

计算机网络篇:基础知识总结与基于长期主义的内容更新
基础知识总结 和 MySQL 类似,我同样花了一周左右的时间根据 csview 对计算机网络部分的八股文进行了整理,主要的内容包括:概述、TCP 与 UDP、IP、HTTP,其中我个人认为最重要的是 TCP 这部分的内容。 在此做一篇目录索引…...

nodejs学习——nodejs和npm安装与系统环境变量配置及国内加速
nodejs和npm安装与系统环境变量配置及国内加速 下载node-v22.14.0-x64.msi 建议修改为非C盘文件夹 其它步骤,下一步,下一步,完成。 打开CMD窗口查看安装详情 $ node -v v22.14.0 $ npm -v 10.9.2$ npm config list创建node_global和node_c…...

《打造视频同步字幕播放网页:从0到1的技术指南》
《打造视频同步字幕播放网页:从0到1的技术指南》 为什么要制作视频同步字幕播放网页 在数字化信息飞速传播的当下,视频已然成为内容输出与获取的核心载体,其在教育、娱乐、宣传推广等诸多领域发挥着举足轻重的作用 。制作一个视频同步字幕播…...

清华大学第八弹:《DeepSeek赋能家庭教育》
大家好,我是吾鳴。 之前吾鳴给大家分享过清华大学出版的七份报告,它们分别是: 《DeepSeek从入门到精通》 《DeepSeek如何赋能职场应用》 《普通人如何抓住DeepSeek红利》 《DeepSeekDeepResearch:让科研像聊天一样简单》 《D…...

自我训练模型:通往未来的必经之路?
摘要 在探讨是否唯有通过自我训练模型才能掌握未来的问题时,文章强调了底层技术的重要性。当前,许多人倾向于关注应用层的便捷性,却忽视了支撑这一切的根本——底层技术。将模型简单视为产品是一种短视行为,长远来看,理…...

C++ Primer 交换操作
欢迎阅读我的 【CPrimer】专栏 专栏简介:本专栏主要面向C初学者,解释C的一些基本概念和基础语言特性,涉及C标准库的用法,面向对象特性,泛型特性高级用法。通过使用标准库中定义的抽象设施,使你更加适应高级…...

深度学习模型组件之优化器--自适应学习率优化方法(Adadelta、Adam、AdamW)
深度学习模型组件之优化器–自适应学习率优化方法(Adadelta、Adam、AdamW) 文章目录 深度学习模型组件之优化器--自适应学习率优化方法(Adadelta、Adam、AdamW)1. Adadelta1.1 公式1.2 优点1.3 缺点1.4 应用场景 2. Adam (Adaptiv…...

使用jcodec库,访问网络视频提取封面图片上传至oss
注释部分为FFmpeg(确实方便但依赖太大,不想用) package com.zuodou.upload;import com.aliyun.oss.OSS; import com.aliyun.oss.model.ObjectMetadata; import com.aliyun.oss.model.PutObjectRequest; import com.zuodou.oss.OssProperties;…...

新品速递 | 多通道可编程衰减器+矩阵系统,如何破解复杂通信测试难题?
在无线通信技术快速迭代的今天,多通道可编程数字射频衰减器和衰减矩阵已成为测试领域不可或缺的核心工具。它们凭借高精度、灵活配置和强大的多通道协同能力,为5G、物联网、卫星通信等前沿技术的研发与验证提供了关键支持。从基站性能测试到终端设备校准…...

扩展------项目中集成阿里云短信服务
引言 在当今数字化时代,短信服务在各种项目中扮演着重要角色,如用户注册验证、订单通知、营销推广等。阿里云短信服务凭借其稳定、高效和丰富的功能,成为众多开发者和企业的首选。本文将详细介绍如何在项目中集成阿里云短信服务,帮…...

MySQL面试篇——性能优化
MySQL性能优化 在MySQL中,如何定位慢查询 慢查询表象:页面加载过慢、接口压测响应时间过长(超过1s)。造成慢查询的原因通常有:聚合查询、多表查询、表数据量过大查询、深度分页查询 方案一:开源工具 调试工…...

Java EE 进阶:Spring MVC(2)
cookie和session的关系 两者都是在客户端和服务器中进行存储数据和传递信息的工具 cookie和session的区别 Cookie是客⼾端保存⽤⼾信息的⼀种机制. Session是服务器端保存⽤⼾信息的⼀种机制. Cookie和Session之间主要是通过SessionId关联起来的,SessionId是Co…...

ShardingSphere 和 Spring 的动态数据源切换机制的对比以及原理
ShardingSphere 与 Spring 动态数据源切换机制的对比及原理 一、核心定位对比 维度ShardingSphereSpring动态数据源(如 AbstractRoutingDataSource)定位分布式数据库中间件轻量级多数据源路由工具核心目标分库分表、读写分离、分布式事务多数据源动态切…...

基于Django的协同过滤算法养老新闻推荐系统的设计与实现
基于Django的协同过滤算法养老新闻推荐系统(可改成普通新闻推荐系统使用) 开发工具和实现技术 Pycharm,Python,Django框架,mysql8,navicat数据库管理工具,vue,spider爬虫࿰…...
)
AI视频生成工具清单(附网址与免费说明)
以下是一份详细的AI视频制作网站总结清单,包含免费/付费信息及核心功能说明: AI视频生成工具清单(附网址与免费说明) 1. Synthesia 网址:https://www.synthesia.io是否免费:免费试用(生成视频…...

JavaWeb学习——HTTP协议
HTTP 协议 什么是 HTTP 协议 HTTP(超文本传输协议,HyperText Transfer Protocol)是用于在客户端(如浏览器)和服务器之间传输超文本(如网页、图片、视频等)的应用层协议。它是现代互联网数据通…...
)
QP 问题(Quadratic Programming, 二次规划)
QP 问题(Quadratic Programming, 二次规划)是什么? QP(Quadratic Programming,二次规划)是一类优化问题,其中目标函数是二次型函数,约束条件可以是线性等式或不等式。 QP 问题是线…...

VSTO(C#)Excel开发2:Excel对象模型和基本操作
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 源码指引:github源…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

dvwa11——XSS(Reflected)
LOW 分析源码:无过滤 和上一关一样,这一关在输入框内输入,成功回显 <script>alert(relee);</script> MEDIUM 分析源码,是把<script>替换成了空格,但没有禁用大写 改大写即可,注意函数…...

【芯片仿真中的X值:隐藏的陷阱与应对之道】
在芯片设计的世界里,X值(不定态)就像一个潜伏的幽灵。它可能让仿真测试顺利通过,却在芯片流片后引发灾难性后果。本文将揭开X值的本质,探讨其危害,并分享高效调试与预防的实战经验。 一、X值的本质与致…...

低代码采购系统搭建:鲸采云+能源行业订单管理自动化案例
在能源行业数字化转型浪潮下,某大型能源集团通过鲸采云低代码平台,仅用3周时间就完成了采购订单管理系统的定制化搭建。本文将揭秘这一成功案例的实施路径与关键成效。 项目背景与挑战 该企业面临: 供应商分散:200供应商使用不同…...
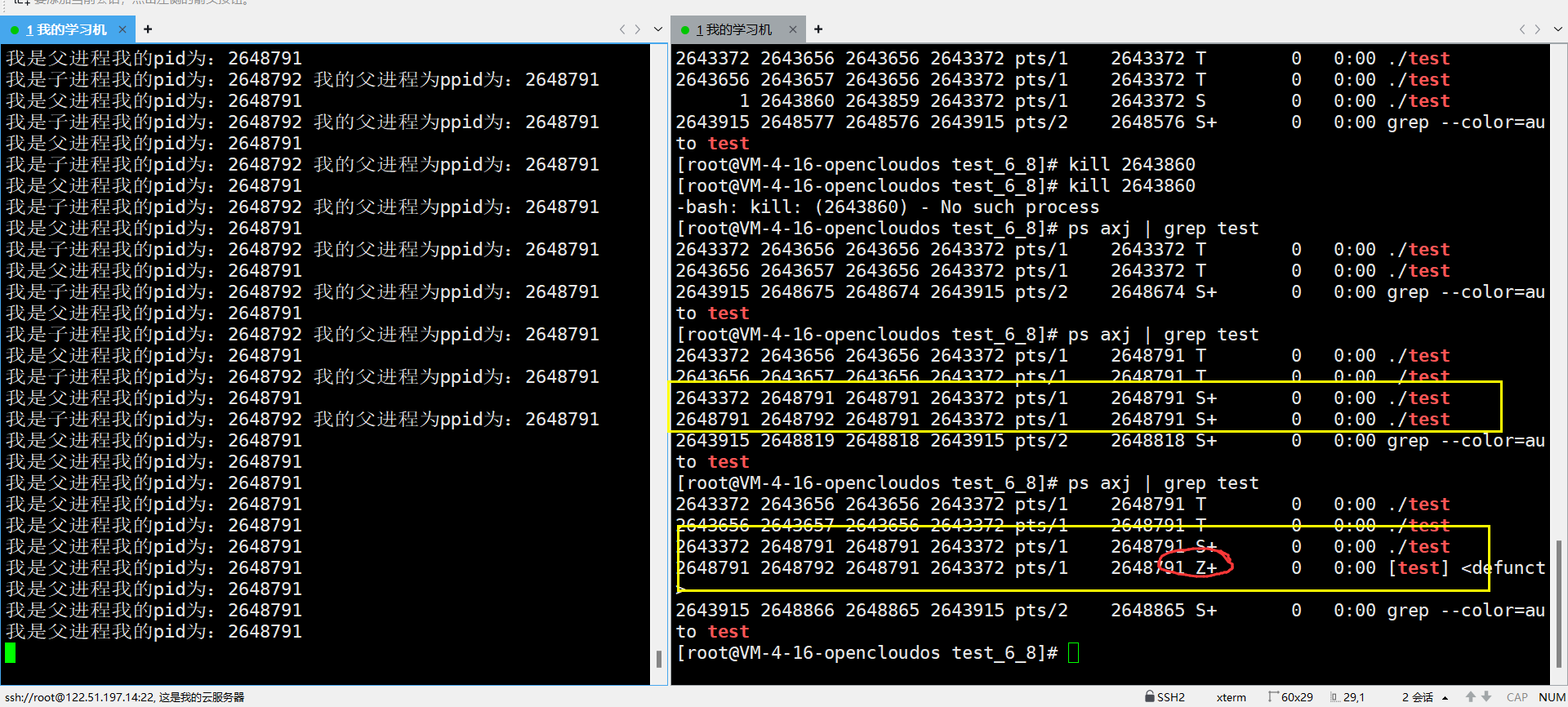
Linux知识回顾总结----进程状态
本章将会介绍进程的一些概念:冯诺伊曼体系结构、进程是什么,怎么用、怎么表现得、进程空间地址、物理地址、虚拟地址、为什么存在进程空间地址、如何感性得去理解进程空间地址、环境变量是如何使用的。 目录 1. 冯诺伊曼体系结构 1.1 是什么 1.2 结论 …...

Go 语言中switch case条件分支语句
1. 基本语法 package main import "fmt" func main() {var extname ".css"switch extname {case ".html":fmt.Println("text/html")case ".css":fmt.Println("text/css") // text/csscase ".js":fmt.…...
