【5】单调队列学习笔记
前言
鸽了很久, 2023 / 1 / 5 2023/1/5 2023/1/5 开始, 2023 / 1 / 21 2023/1/21 2023/1/21 才完工。
中途去集训了,没时间来补漏洞。
单调队列
单调队列是一种非常实用的数据结构,可以用于查询一个定长区间在以一定速度向后滑动,并查询区间内最值的问题(具体见例题 1 1 1 )。时间复杂度非常低,总体是 O ( n ) O(n) O(n) ,均摊到每个元素是 O ( 1 ) O(1) O(1) ,所以常用来优化其他算法。
单调队列需要保证队列元素的单调性,也就是说,要保证队头就是最值,这样就可以做到 O ( 1 ) O(1) O(1) 查询最值。
单调队列的维护:
1 1 1 :向后滑动的过程中,会有新的元素加入队列。这时候,为了保证队列单调性,就应该把新元素与队尾元素比较大小。如果比队尾元素更接近最值,那么表示这个元素既比队尾元素优,又比队尾元素的时间晚,队尾元素会在这个元素之前被移出区间。这时存储这个元素就没有必要,可以直接前移队尾指针,把队尾元素移除队列。重复执行直到队列为空或该元素不比队尾元素优,最后该元素入队。
2 2 2 :向后滑动的过程中,会有旧的元素退出队列。可以记录每个元素的入队位置,根据现在的位置和队列长度计算出队首元素是否退出队列。如果退出,可以后移队头指针,将队首元素出队。重复执行直到队首元素满足要求。
具体代码详见各题目。
单调队列例题
例题 1 1 1 :
P1886 滑动窗口 /【模板】单调队列
单调队列模板题,不多赘述。
此处用的是 for 循环,代码比较冗余,简洁的模板请见其他题目。
#include <bits/stdc++.h>
using namespace std;
int n,k,a[2000050],heads=0,tails=0,headb=0,tailb=0;
struct node
{int v,t;
}stb[2000050],sts[2000050];inline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}int main()
{n=read();k=read();for(int i=1;i<=n;i++)a[i]=read();sts[++heads].t=1;sts[heads].v=a[1];tails++;if(k==1)printf("%d ",sts[heads].v);for(int i=2;i<=n;i++){for(int j=tails;a[i]<sts[j].v&&j>=heads;j--)tails--;sts[++tails].t=i;sts[tails].v=a[i];for(int j=heads;j<=tails&&i-sts[j].t>=k;j++)heads++;if(i>=k)printf("%d ",sts[heads].v);}printf("\n");stb[++headb].t=1;stb[headb].v=a[1];tailb++;if(k==1)printf("%d ",stb[headb].v);for(int i=2;i<=n;i++){for(int j=tailb;a[i]>stb[j].v&&j>=headb;j--)tailb--;stb[++tailb].t=i;stb[tailb].v=a[i];for(int j=headb;j<=tailb&&i-stb[j].t>=k;j++)headb++;if(i>=k)printf("%d ",stb[headb].v);}return 0;
}
例题 2 2 2 :
P3088 [USACO13NOV]Crowded Cows S
如果一头奶牛 D D D 范围内的最高奶牛都不是它的两倍,那么这头奶牛就不会拥挤。所以可以通过查询最大值来确定是否会拥挤,就转化为了滑窗最大值问题。
首先把奶牛按照 x i x_i xi 升序排列,然后以 x i x_i xi 为位置, h i h_i hi 为值建立单调队列查询最大值,队列长度为 D D D 。单调队列需要正着跑一遍,反着跑一遍,求出两边的最大值。
注意这里是先计算,再插入值。因为奶牛自己不会拥挤自己。
当然不这样也可以,因为奶牛自己的身高不会是自己的 2 2 2 倍以上。
#include<bits/stdc++.h>
using namespace std;
struct cow
{long long h,x;
}c[300000],que[300000];
long long n,d,cnt=0;
bool book1[300000],book2[300000];
bool cmp(struct cow a,struct cow b)
{return a.x<b.x;
}int main()
{scanf("%lld%lld",&n,&d);for(long long i=0;i<n;i++)scanf("%lld%lld",&c[i].x,&c[i].h);sort(c,c+n,cmp);long long head=0,tail=0;que[++tail]=c[0];head++;for(long long i=1;i<n;i++){while(que[head].x<c[i].x-d&&head<=tail)head++;if(que[head].h>=c[i].h*2)book1[i]=1;while(que[tail].h<=c[i].h&&tail>=head)tail--;que[++tail]=c[i];}head=0;tail=0;que[++tail]=c[n-1];head++;for(long long i=n-2;i>=0;i--){while(que[head].x>c[i].x+d&&head<=tail)head++;if(que[head].h>=c[i].h*2)book2[i]=1;while(que[tail].h<=c[i].h&&tail>=head)tail--;que[++tail]=c[i];}for(long long i=0;i<n;i++)if(book1[i]&&book2[i])cnt++;printf("%lld\n",cnt);return 0;
}
例题 3 3 3 :
P2698 [USACO12MAR]Flowerpot S
答案是满足单调性的。越宽的花盆,可以得到的答案就越大。反之亦然。所以可以通过二分答案来做。
验证答案时,由于需要查询最值,而花盆长度固定,可以假设花盆从左向右滑动,最后的答案是每次滑动后最大值与最小值的差的最大值,实际上就是枚举花盆的结束点。所以就转化为了滑窗最值问题,可以跑两遍单调队列。一遍跑最大值,一遍跑最小值。
把奶牛按照 x i x_i xi 升序排列,然后以 x i x_i xi 为位置, y i y_i yi 为值建立单调队列查询最大值和最小值,队列长度为二分查找时的 m i d mid mid 。最后把每次滑动后最大值与最小值的差的最大值与 D D D 比较,就能知道答案的正确性了。
注意,如果一个答案合理,那么还可以尝试更小的花盆,不能直接退出。
听说ST表也能做,但是效率绝对没有单调队列高。
#include <bits/stdc++.h>
using namespace std;
struct drop
{int x,y;
}water[100010],que[300010];
int n,d,l=1,r=99999999,ans=-1,h=0,t=0;
int maxn[1000100],minn[1000100];
bool cmp1(struct drop a,struct drop b)
{return a.x<b.x;
}bool check(int l)
{int ans=0;memset(maxn,0,sizeof(maxn));memset(minn,0,sizeof(minn));h=0;t=0;que[++h].x=water[0].y;que[++t].y=water[0].x;maxn[0]=water[0].y;for(int i=1;i<n;i++){while(que[t].x<=water[i].y&&h<=t)t--;que[++t].x=water[i].y;que[t].y=water[i].x;while(water[i].x-que[h].y>l&&h<=t)h++;maxn[i]=que[h].x;}h=0;t=0;que[++h].x=water[0].y;que[++t].y=water[0].x;minn[0]=water[0].y;for(int i=1;i<n;i++){while(que[t].x>=water[i].y&&h<=t)t--;que[++t].x=water[i].y;que[t].y=water[i].x;while(water[i].x-que[h].y>l&&h<=t)h++;minn[i]=que[h].x;}for(int i=0;i<n;i++)ans=max(ans,maxn[i]-minn[i]);return ans>=d;
}int main()
{scanf("%d%d",&n,&d);for(int i=0;i<n;i++)scanf("%d%d",&water[i].x,&water[i].y);sort(water,water+n,cmp1);while(l<r){int mid=(l+r)/2;if(check(mid))ans=mid,r=mid;else l=mid+1;}printf("%d",ans);return 0;
}
单调队列的运用
单调队列是可以用来优化DP的,可以把一部分 O ( n 2 ) O(n^2) O(n2) 的DP优化到 O ( n ) O(n) O(n) ,是一个非常大的优化。
当然,想使用单调队列优化DP,还是需要一定的想象力的。
例题 4 4 4 :
P1725 琪露诺
很容易写出这样一个转移方程:
d p [ i ] = max { d p [ i − j ] } + a [ i ] ( L ≤ j ≤ R ) dp[i]=\max\{dp[i-j]\}+a[i](L\le j\le R) dp[i]=max{dp[i−j]}+a[i](L≤j≤R)
如果这样子朴素转移,时间复杂度是 O ( n ( L − R ) ) O(n(L-R)) O(n(L−R)) 的,很容易超时。
我们观察到, j j j 的取值范围 ( L ≤ j ≤ R ) (L\le j\le R) (L≤j≤R) 是不变的,也就意味着可以取的 d p [ i − j ] dp[i-j] dp[i−j] 的个数是不变的。又因为 j j j 在取值范围 ( L ≤ j ≤ R ) (L\le j\le R) (L≤j≤R) 中是连续自然数,所以 d p [ i − j ] dp[i-j] dp[i−j] 是连续的。 d p [ i − j ] dp[i-j] dp[i−j] 的取值就像一个固定长度的窗口。
d p [ i − j ] dp[i-j] dp[i−j] 中,我们需要逐个递增枚举 i i i 。那么此时 d p [ i − j ] dp[i-j] dp[i−j] 的取值也会随之逐个递增,就像一个固定长度的滑动窗口。就像这样:

对这是滑动窗口的原图
而此时需要求的就是 d p [ i − j ] dp[i-j] dp[i−j] 的取值中的最大值,可以使用单调队列来维护。
注意如果 i < L i\lt L i<L ,证明无法跳到这个格子,可以赋值为负无穷,排除干扰。
#include <bits/stdc++.h>
using namespace std;
int n,l,r,a[2000050],f[2000050],head=0,tail=0,ans=-99999999;
struct node
{int t,v;
}que[2000050];inline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}int main()
{n=read();l=read();r=read();for(int i=1;i<=n+1;i++)a[i]=read();que[++tail].t=1;que[tail].v=a[1];head++;f[1]=a[1];for(int i=2;i<=n+r+1;i++){f[i]=-99999999;if(i>l){while(que[tail].v<=f[i-l]&&tail>=head)tail--;que[++tail].t=i-l;que[tail].v=f[i-l];while(que[head].t<i-r&&head<=tail)head++;f[i]=que[head].v+a[i];}}for(int i=n+1;i<=n+r+1;i++)ans=max(ans,f[i]);printf("%d",ans);return 0;
}
例题 5 5 5 :
P2034 选择数字
双倍经验
P2627 [USACO11OPEN]Mowing the Lawn G
正着DP不好想,不如正难则反,要使选出的数字的和最大,就是要不选的数字和最小。
很容易写出这样一个逆向DP的转移方程:
d p [ i ] = min { d p [ i − j ] } + a [ i ] ( 0 < j ≤ k ) dp[i]=\min\{dp[i-j]\}+a[i](0\lt j\le k) dp[i]=min{dp[i−j]}+a[i](0<j≤k)
依据例题 4 4 4 的分析,这个式子也可以用单调队列来维护 min { d p [ i − j ] } \min\{dp[i-j]\} min{dp[i−j]} ,把时间复杂度降为 O ( n ) O(n) O(n) 。
P2034
#include <bits/stdc++.h>
using namespace std;
long long n,k,a[2000050],f[2000050],head=0,tail=0,ans=99999999999999,tol=0;
struct node
{long long t,v;
}que[2000050];inline long long read()
{long long x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}int main()
{n=read();k=read();for(long long i=0;i<n;i++){a[i]=read();tol+=a[i];}que[++tail].t=0;que[tail].v=a[0];head++;f[0]=a[0];for(long long i=1;i<n;i++){if(i-k-1>=0){while(que[head].t<i-k-1&&head<=tail)head++;f[i]=que[head].v;}f[i]+=a[i];while(que[tail].v>f[i]&&head<=tail)tail--;que[++tail].v=f[i];que[tail].t=i;}for(long long i=n-k-1;i<n;i++)ans=min(f[i],ans);printf("%lld",tol-ans);return 0;
}
P2627
#include <bits/stdc++.h>
using namespace std;
long long n,k,a[2000050],f[2000050],head=0,tail=0,ans=99999999999999,tol=0;
struct node
{long long t,v;
}que[2000050];inline long long read()
{long long x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}int main()
{n=read();k=read();for(long long i=0;i<n;i++){a[i]=read();tol+=a[i];}que[++tail].t=0;que[tail].v=a[0];head++;f[0]=a[0];for(long long i=1;i<n;i++){if(i-k-1>=0){while(que[head].t<i-k-1&&head<=tail)head++;f[i]=que[head].v;}f[i]+=a[i];while(que[tail].v>f[i]&&head<=tail)tail--;que[++tail].v=f[i];que[tail].t=i;}for(long long i=n-k-1;i<n;i++)ans=min(f[i],ans);printf("%lld",tol-ans);return 0;
}
后记
单调队列还是很需要想象力的,否则没有那么好理解。
顺便纪念一下,这是我农历虎年的最后一篇博客!
相关文章:

【5】单调队列学习笔记
前言 鸽了很久, 2023 / 1 / 5 2023/1/5 2023/1/5 开始, 2023 / 1 / 21 2023/1/21 2023/1/21 才完工。 中途去集训了,没时间来补漏洞。 单调队列 单调队列是一种非常实用的数据结构,可以用于查询一个定长区间在以一定速度向后滑…...

deepseek为什么要开源
一、生态位的抢占与锁定:以 JDK 版本为例 在软件开发的世界里,生态位的抢占和先入为主的效应十分显著。就拿 Java 开发中的 JDK 版本来说,目前大多数开发者仍在广泛使用 JDK8。尽管 JDK17 和 JDK21 已经推出,且具备更多先进特性…...

MySQL基本建表操作
目录 1,创建数据库db_ck 1.1创建表 1.2 查看创建好的表 2,创建表t_hero 2.1 先进入数据库Db_Ck 2.1.1 这里可以看是否进入数据库: 2.2 创建表t_Hero 2.2.1 我们可以先在文本文档里面写好然后粘贴进去,因为直接写的话,错了要重新开始 …...

防火墙旁挂组网双机热备负载均衡
一,二层交换网络: 使用MSTPVRRP组网形式 VLAN 2--->SW3为主,SW4 作为备份 VLAN 3--->SW4为主,SW3 作为备份 MSTP 设计 --->SW3 、 4 、 5 运行 实例 1 : VLAN 2 实例 2 : VLAN 3 SW3 是实例 1 的主根,实…...

大白话react第十八章React 与 WebGL 项目的高级拓展与优化
大白话react第十八章React 与 WebGL 项目的高级拓展与优化 1. 实现 3D 模型的导入与动画 在之前的基础上,我们可以导入更复杂的 3D 模型,并且让这些模型动起来,就像在游戏里看到的角色和场景一样。这里我们使用 GLTF 格式的模型,…...

JavaScript系列06-深入理解 JavaScript 事件系统:从原生事件到 React 合成事件
JavaScript 事件系统是构建交互式 Web 应用的核心。本文从原生 DOM 事件到 React 的合成事件,内容涵盖: JavaScript 事件基础:事件类型、事件注册、事件对象事件传播机制:捕获、目标和冒泡阶段高级事件技术:事件委托、…...

C++:string容器(下篇)
1.string浅拷贝的问题 // 为了和标准库区分,此处使用String class String { public :/*String():_str(new char[1]){*_str \0;}*///String(const char* str "\0") // 错误示范//String(const char* str nullptr) // 错误示范String(const char* str …...

2.数据结构-栈和队列
数据结构-栈和队列 2.1栈2.1.1栈的表示和实现2.1.2栈的应用举例数制转换括号匹配检验迷宫给求解表达式求值 2.1.3链栈的表示和实现2.1.4栈与递归的实现遍历输出链表中各个结点的递归算法*Hanoi塔问题的递归算法 2.2队列2.2.1循环队列——队列的顺序表示和实现2.2.2链队——队列…...

aws(学习笔记第三十一课) aws cdk深入学习(batch-arm64-instance-type)
aws(学习笔记第三十一课) aws cdk深入学习 学习内容: 深入练习aws cdk下部署batch-arm64-instance-type 1. 深入练习aws cdk下部署batch-arm64-instance-type 代码链接 代码链接 代码链接 -> batch-arm64-instance-type之前代码学习 之前学习代码链接 -> aw…...

MySQL 中,SELECT ... FOR UPDATE
在 MySQL 中,SELECT ... FOR UPDATE 语句会对查询结果集中的行加排他锁(X 锁)。关于其他事务是否能读取当前行,以下是详细说明: 1. 排他锁(X 锁)的特性 排他锁是一种独占锁,加锁后&…...

云服务运维智能时代:阿里云操作系统控制台
阿里云操作系统控制台 引言需求介绍操作系统使用实例获得的帮助与提升建议 引言 阿里云操作系统控制台是一款创新型云服务器运维工具,专为简化用户的运维工作而设计。它采用智能化和可视化的方式,让运维变得更加高效、直观。借助AI技术,控制…...

【Agent的革命之路——LangGraph】如何使用config
有时我们希望在调用代理时能够对其进行配置。这包括配置使用哪个语言模型(LLM)等例子。下面我们将通过一个示例来详细介绍如何进行这样的配置。 在介绍 configurable 之前我们先介绍一下 Langchain 的 RunnableConfig。RunnableConfig是一个配置对象&…...

ArcGIS操作:15 计算点的经纬度,并添加到属性表
注意:需要转化为地理坐标系 1、打开属性表,添加字段 2、计算字段(以计算纬度为例 !Shape!.centroid.Y ) 3、效果...

Docker基础入门
第 1 章:核心概念与安装配置 本章首先介绍Docker 的三大核心概念: 镜像 (Image)容器(Container)仓库(Repository) 只有理解了这三个核心概念,才能顺利地理解Docker容器的整个生命周期。 随后࿰…...

【Linux】详谈 基础I/O
目录 一、理解文件 狭义的理解: 广义理解: 文件操作的归类认知 系统角度 二、系统文件I/O 2.1 标志位的传递 系统级接口open 编辑 open返回值 写入文件 读文件 三、文件描述符 3.1(0 & 1 & 2) 3.2 文件描…...

爬虫案例七Python协程爬取视频
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Python协程爬取视频 前言 提示:这里可以添加本文要记录的大概内容: 爬虫案例七协程爬取视频 提示:以下是本篇文章正文…...

[20250304] 关于 RISC-V芯片 的介绍
[20250304] 关于 RISC-V芯片 的介绍 1. 调研报告 一、RISC-V 芯片结构分析 RISC-V 芯片基于开源指令集架构(ISA),其核心优势在于模块化设计与高度灵活性。 指令集架构 基础指令集:包含 RV32I(32 位)、R…...
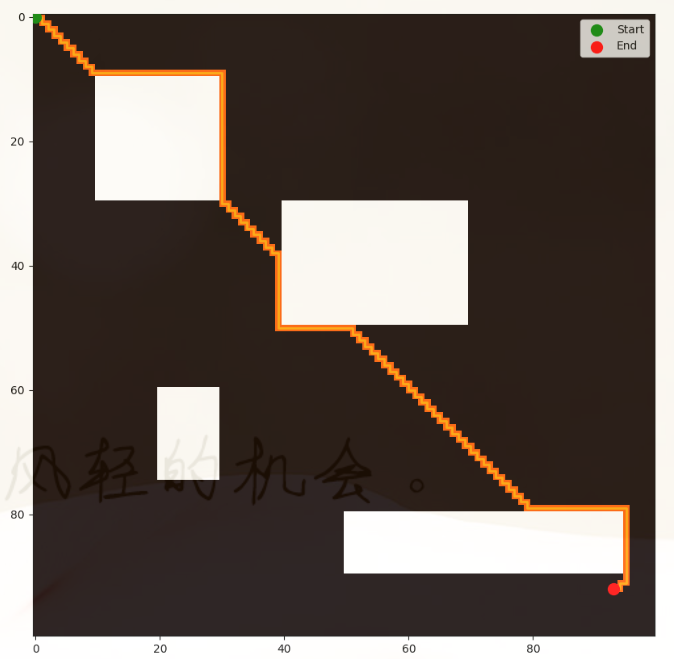
一学就会:A*算法详细介绍(Python)
📢本篇文章是博主人工智能学习以及算法研究时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在&am…...
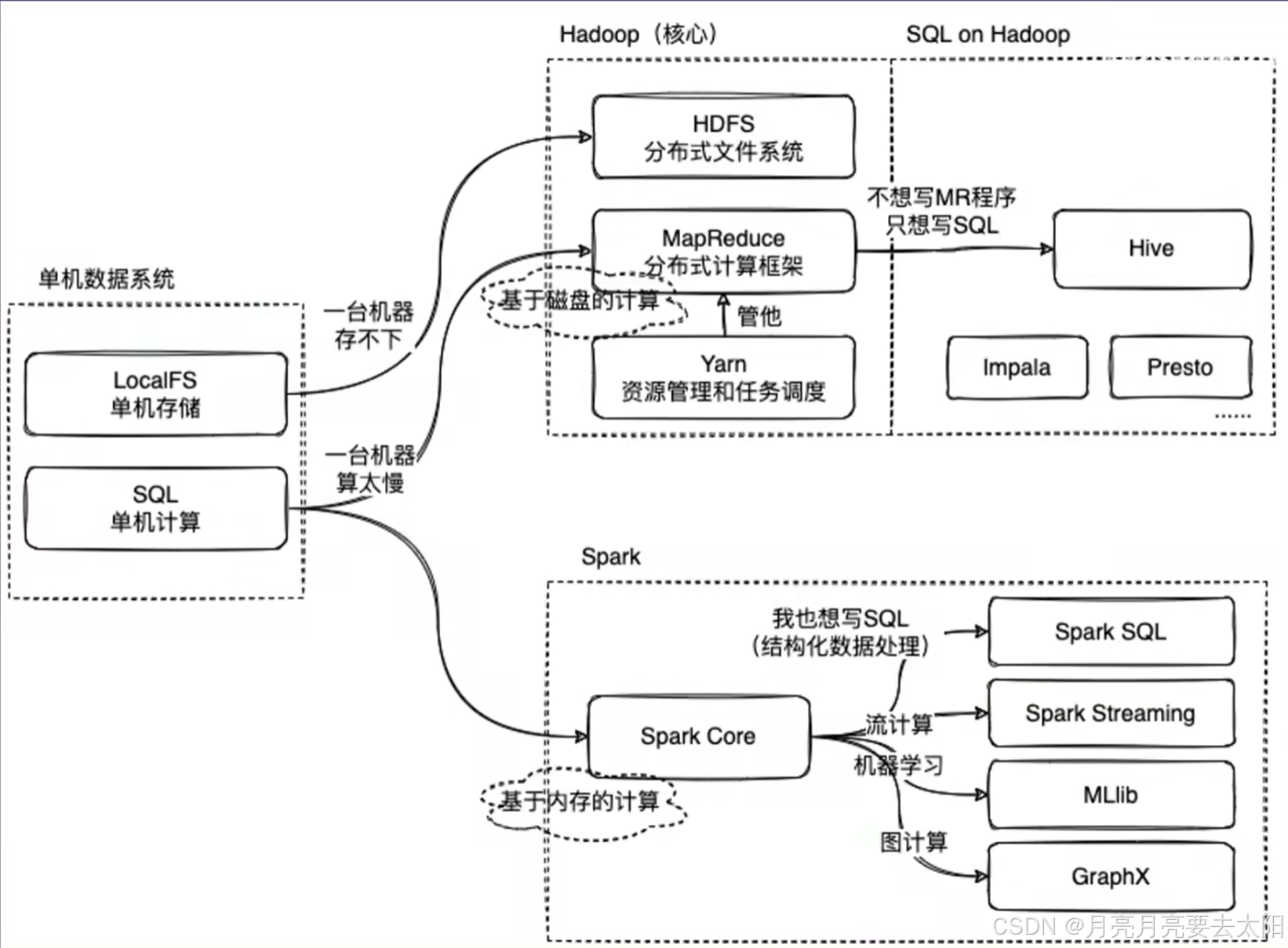
Hadoop、Hive、Spark的关系
Part1:Hadoop、Hive、Spark关系概览 1、MapReduce on Hadoop 和spark都是数据计算框架,一般认为spark的速度比MR快2-3倍。 2、mapreduce是数据计算的过程,map将一个任务分成多个小任务,reduce的部分将结果汇总之后返回。 3、HIv…...

Excel·VBA江西省预算一体化工资表一键处理
每月制作工资表导出为Excel后都需要调整格式,删除0数据的列、对工资表项目进行排序、打印设置等等,有些单位还分有“行政”、“事业”2个工资表就需要操作2次。显然,这种重复操作的问题,可以使用VBA代码解决 目录 代码使用说明1&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...

前端异步编程全场景解读
前端异步编程是现代Web开发的核心,它解决了浏览器单线程执行带来的UI阻塞问题。以下从多个维度进行深度解析: 一、异步编程的核心概念 JavaScript的执行环境是单线程的,这意味着在同一时间只能执行一个任务。为了不阻塞主线程,J…...
