0204强连通性-有向图-数据结构和算法(Java)
文章目录
- 1 概述
- 2 强连通分量
- 2.1 定义
- 2.2 Kosaraju算法
- 2.2.1 算法实现
- 2.2.2算法测试
- 2.2.3 算法理解
- 3 强连通性
- 结语
1 概述
定义。如果2个顶点是相互可达的,则称它们为强连通的。如果一幅有向图中的任意两个顶点都是强连通的,则称这幅有向图也是强连通的。
环在强连通的理解上起着重要的作用。
两个顶点时强连通的当且仅当它们都在一个普通的有向环中。
2 强连通分量
2.1 定义
有向图中的强连通性也是一种顶点之间的定价关系,因为它有着以下性质。
- 自反性:任意顶点v都是和自己强连通的。
- 对称性:如果v和w是强连通的,那么w和v也是强连通的。
- 传递性: 如果v和w是强连通的且w和x是强连通的,那么v和x也是强连通的。
做为一种等价关系,强连通性将所有顶点分为了一些等价类,每个等价类都是由相互均为强连通的顶点的最大子集组成的。我们将这些子集称为强连通分量。
在有向图中,强连通分量是指有向图中的一个最大的强连通子图。也就是说,它是一个包含尽可能多的节点的强连通子图,并且无法再添加任何其他节点使其变成更大的强连通子图。
2.2 Kosaraju算法
2.2.1 算法实现
Kosaraju算法就是用来在有向图中计算强连通分量的,算法如下:
- 在给定的一幅有向图G中,计算她的反向图的逆后序排序;
- 在G中进行标准的深度优先搜索,但是要按照刚才计算得到的顺序而非标准的顺序来访问所有未被标记的顶点。
- 一次dfs()方法调用中被访问到的顶点都在同一个强连通分量重,将它们按照和之前无向图处理连通分量一样的方式识别出来。
算法非递归实现代码2.2.1-1如下所示:
package com.gaogzhen.datastructure.graph.directed;import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Digraph;
import edu.princeton.cs.algs4.TransitiveClosure;import java.util.Iterator;/*** 计算强连通分量* @author gaogzhen*/
public class KosarajuSharirSCC {/*** 访问标记*/private boolean[] marked;/*** 连通分量标记*/private int[] id;/*** 连通分量数量*/private int count;/*** 计算强连通分量* @param digraph 有向图*/public KosarajuSharirSCC(Digraph digraph) {// compute reverse postorder of reverse graphDepthFirstOrder dfs = new DepthFirstOrder(digraph.reverse());// run DFS on digraph, using reverse postorder to guide calculationmarked = new boolean[digraph.V()];id = new int[digraph.V()];for (int v : dfs.reversePost()) {if (!marked[v]) {dfs(digraph, v);count++;}}// check that id[] gives strong componentsassert check(digraph);}/*** 深度优先搜索计算强连通分量* @param digraph 优先图* @param s 起点*/private void dfs(Digraph digraph, int s) {// 栈记录搜索路径Stack<Iterator<Integer>> path = new Stack<>();if (!marked[s]) {// 起点默认没标记,可以不加是否标记判断marked[s] = true;id[s] = count;Iterable<Integer> iterable = digraph.adj(s);Iterator<Integer> it;if (iterable != null && (it = iterable.iterator()) != null){// 顶点对应的邻接表迭代器存入栈path.push(it);}}while (!path.isEmpty()) {Iterator<Integer> it = path.pop();int x;while (it.hasNext()) {// 邻接表迭代器有元素,获取元素x = it.next();if (!marked[x]) {// 顶点未被标记,标记marked[x] = true;id[x] = count;if (it.hasNext()) {// 邻接表迭代器有元素重新入栈path.push(it);}// 深度优先原则,当前迭代器入栈,新标记顶点的邻接表迭代器入栈,下次循环优先访问Iterable<Integer> iterable = digraph.adj(x);if (iterable != null && (it = iterable.iterator()) != null){path.push(it);}break;}}}}/*** 连通分量数量* @return 连通分量数量*/public int count() {return count;}/*** 顶点v和w是强连通的吗* @param v 顶点v* @param w 顶点w* @return {@code true} if vertices {@code v} and {@code w} are in the same* strong component, and {@code false} otherwise* @throws IllegalArgumentException unless {@code 0 <= v < V}* @throws IllegalArgumentException unless {@code 0 <= w < V}*/public boolean stronglyConnected(int v, int w) {validateVertex(v);validateVertex(w);return id[v] == id[w];}/*** 顶点v所在的强连通分量标记* @param v 指定顶点v* @return the component id of the strong component containing vertex {@code v}* @throws IllegalArgumentException unless {@code 0 <= s < V}*/public int id(int v) {validateVertex(v);return id[v];}/**** @param digraph 有向图* @return*/private boolean check(Digraph digraph) {TransitiveClosure tc = new TransitiveClosure(digraph);for (int v = 0; v < digraph.V(); v++) {for (int w = 0; w < digraph.V(); w++) {if (stronglyConnected(v, w) != (tc.reachable(v, w) && tc.reachable(w, v))) {return false;}}}return true;}/*** 校验顶点v* @param v 顶点v*/private void validateVertex(int v) {int V = marked.length;if (v < 0 || v >= V) {throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}}
}
算法实现相对简单,但是理解起来有些费劲,兄弟被这个问题困扰了好几天。通过参考底下链接[2][3]加上之前内容学习,才解开疑惑。
2.2.2算法测试
以下图2.2.2-1所示有向图为例:

测试代码如下2.2.2-1所示:
public static void testKosaraju() {String path = System.getProperty("user.dir") + File.separator + "asserts/tinyDG1.txt";In in = new In(path);Digraph digraph = new Digraph(in);KosarajuSharirSCC scc = new KosarajuSharirSCC(digraph);// number of connected componentsint m = scc.count();StdOut.println(m + " strong components");// compute list of vertices in each strong componentQueue<Integer>[] components = (Queue<Integer>[]) new Queue[m];for (int i = 0; i < m; i++) {components[i] = new Queue<Integer>();}for (int v = 0; v < digraph.V(); v++) {components[scc.id(v)].enqueue(v);}// print resultsfor (int i = 0; i < m; i++) {for (int v : components[i]) {StdOut.print(v + " ");}StdOut.println();}
}
- 有兴趣可以把全部连通分量分组封装为一个方法
测试结果:
5 strong components
1
0 2 3 4 5
9 10 11 12
6
7 8
2.2.3 算法理解
最开始关于算法的疑惑:
- 深度优先搜索算法下,一个连通分量只要有顶点出度,必然会去访问非当前连通分量中的顶点,怎么确定连通分量的分界呢?
- 反向图的逆后序排列和原有向图有啥关系,这样的话不用费劲先构建反向图获取反向图的逆后序排列,在去深度优先搜索原图
下面是一些我们来一步一步分析:
- 前置知识点
- 有向无环图有n个顶点对应有n个连通分量,即一个顶点对应一个连通分量;
- 有向环中顶点在同一连通分量内,那么有向图和其反向图具有相同的连通分量。
- 我们知道强连通分量中顶点是等价的,可以把同一强连通分量看作一个顶点,该顶点称为该强连通分量的缩点。
- 有向图的逆后序排列就是有向边优先从排在前面的元素指向排在后面的元素
如下图2.2.3-1所示,为我们在#2.2.2中示例有向图对应的连通分量:

第一步,我们先来分析连通分量与连通分量之间的关系。
下面我们把同一连通分量做成一个缩点,如下图2.2.3-2所示:
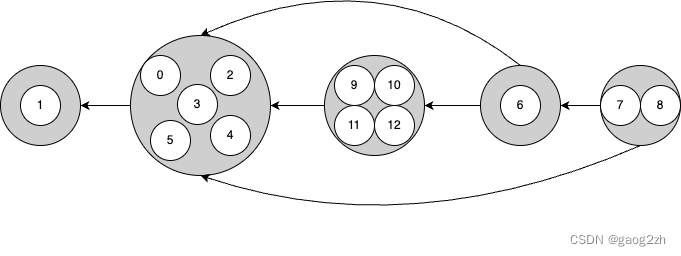
我们期望的访问访问顺序1所在的连通分量->0所在的连通分量->9所在的连通分量->6所在的连通分量->7所在的连通分量。这样在访问后面的连通分量时,即使有指出的连接,它所指向的连通分量顶点已经被标记访问过,即当前访问的顶点一定在同一连通分量内。
如何确定访问顺序呢?很容易想到逆后序排列可以实现,但是我们需要后指向优先,所以我们需要调转原有的方向,即我们先得到有向图G的反向图GRG^RGR 的逆后序排列,在按照该顺序深度优先搜索有向图G。
一次dfs()调用,确定一个连通分量。
第二步,我们来分析连通分量内部顶点之间的关系。
上面解释了不同连通分量之间的问题,下面还有两个问题,关于同一连通分量内的顶点:
- (1)每个和s强连通的顶点v都会在一次dfs(G,s)中被访问到?
- (2)一次dfs调用的dfs(G,s)所到达的任意顶点v都必然是和s强连通的?
证明:
(1) 反证法假设“有一个和s强连通的顶点v不在dfs(G,s)中被访问到“。因为存在从s到v的路径,所以v肯定在之前就已经被标记过。但是因为也存在从v到s到路径,在dfs(G,v)的调用中s肯定会被标记,因此构造函数应该是不会调用dfs(G,s)的。矛盾。
(2)设v为dfs(G,s)到达的某个顶点。那么G中必然存在一条从s到v的路径,因此只需要证明G中还存在一条从v到s到路径即可。这也等价于证明GRG^RGR 中存在一条从s到v的路径。
证明的核心在于,按照逆后序进行的深度优先搜索意味着,在GRG^RGR中进行的深度优先搜索中,dfs(G,v)必然在dfs(G,s)之前就已经结束了,这样dfs(G,v)的调用就只会出现两种情况:
- 调用在dfs(G,s)的调用之前(并且也在dfs(G,s)的调用之前结束)
- 调用在dfs(G,s)的调用之后(并且也在dfs(G,s)的结束之前结束)
第一种情况是不可能存在的,因为在GRG^RGR中存在一从v到s到路径;而第二中情况则说明GRG^RGR中存在一条从s到v的路径。
上述证明摘自书中,第一条证明很容易理解,但是第二条证明看得有我使劲挠头也没能理解。主要是没能给区分出我们要找的s到v和v到s 是在哪里找。
首先证明一次dfs(G,s)所到达的任意顶点都是和s强连通的,很明显存在从s到v的路径,即先遍历s后遍历v,这个顺序是从反向图GRG^RGR 的逆后序排列获得的;G中存在从s到v的路径,那么反向图GRG^RGR中必然存在从v到s到路径,按照逆后序排列,顺序应该是先v在s;那么有向图G的dfs调用中顶点v必然先于顶点s被被标记,也就不可能存在从s到v的路径,所以GRG^RGR中必然存在从s到v的路径,即G存在从v到s到路径。
那么G中s顶点可达但是不在同一连通分量中的顶点呢?这些属于其他连通分量的顶点,根据之前讲述的连通分量与连通分量之间的讨论,必然先于顶点s被标记。
不知道该算法当初是怎么被发现的呢?真好奇,这个问题困扰了我好几天了。
3 强连通性
强连通性:给定一幅有向图,回答“给定的两个顶点是强连通的吗?这幅有向图中含有多个强连通分量?”等类似问题
命题I。Kosaraju算法等预处理所需时间和空间与V+E成正比且支持常数时间等有向图强连通性的查询。
证明。该算法会处理有向图的反向图并进行两次深度优先搜索。这3步骤所需的时间都与V+E成正比。
结语
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p378-383.
[2]图解:有向环、拓扑排序与 Kosaraju 算法[CP/OL].
[3]如何理解Kosaraju算法?[CP/OL].
相关文章:

0204强连通性-有向图-数据结构和算法(Java)
文章目录1 概述2 强连通分量2.1 定义2.2 Kosaraju算法2.2.1 算法实现2.2.2算法测试2.2.3 算法理解3 强连通性结语1 概述 定义。如果2个顶点是相互可达的,则称它们为强连通的。如果一幅有向图中的任意两个顶点都是强连通的,则称这幅有向图也是强连通的。 …...
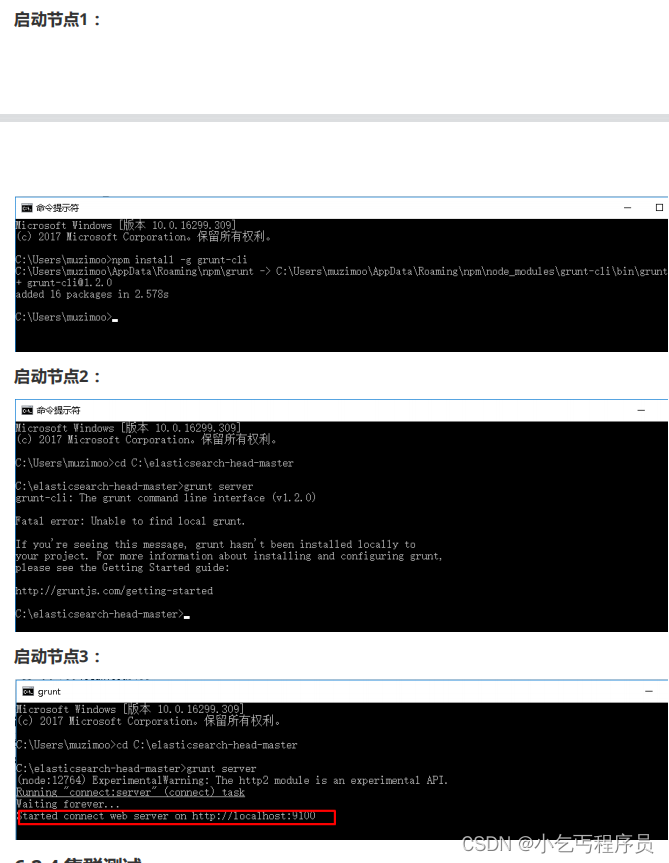
ElasticSearch集群
5.2 IK分词器简介 IKAnalyzer是一个开源的,基于java语言开发的轻量级的中文分词工具包。从2006年12月推出1.0版开始,IKAnalyzer已经推出 了3个大版本。最初,它是以开源项目Lucene为应用主体的,结合词典分词和文法分析算法的中文分…...
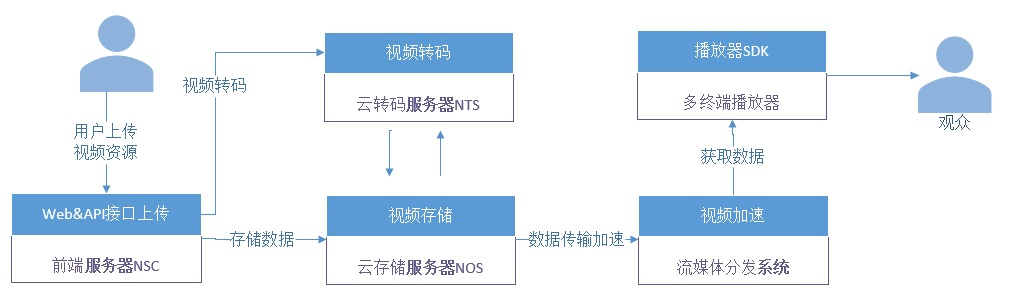
音视频基础概念(6)——视频基础
网上冲浪时,我们会接触到网络流媒体和本地视频文件。常见的视频文件格式有MP4、MKV、AVI等。在流媒体网站上看见视频常用的协议有HTTP、RTSP、RTMP、HLS等。视频技术较为复杂,包括视频封装、视频编解码、视频播放和视频转码等内容。1 视频基础概念当下市…...

【Python网络蜘蛛】基础 - 多线程和多进程的基本原理
文章目录多线程和多进程的基本原理多线程的含义并发和并行Python中的多线程和多进程多线程和多进程的基本原理 在编写爬虫程序的时候,为了提高爬取效率,我们可能会同时运行多个爬虫任务,其中同样涉及多进程和多线程。 多线程的含义 先了解一…...

linux C/C++文件路径操作
标题1、 access函数查找文件夹是否存在/文件是否有某权限 头文件: 在windows环境下头文件为: #include <io.h> 在linux环境下头文件为: #include <unistd.h> 函数原型: int access(const char* _Filename, int _Acce…...
)
Baumer工业相机堡盟相机如何使用BGAPI SDK和Opencv联动实现图像转换成视频(C#)
Baumer工业相机堡盟相机如何使用BGAPI SDK和Opencv联动实现图像转换成视频Baumer工业相机Baumer工业相机SDK技术背景代码分析第一步:先引用OpenCV库第二步:引用图像文件夹生成视频工业相机图像通过OpenCV转为视频的优点工业相机图像转为视频的行业应用…...

Redis常用命令以及如何在Java中操作Redis
前言Redis是一个基于内存的key-value结构数据库,是互联网技术领域使用最为广泛的存储中间件。Redis基于内存存储,读写性能高,适合存储热点数据(热点商品、资讯、新闻)。Redis是一个开源的内存中的数据结构存储系统&…...
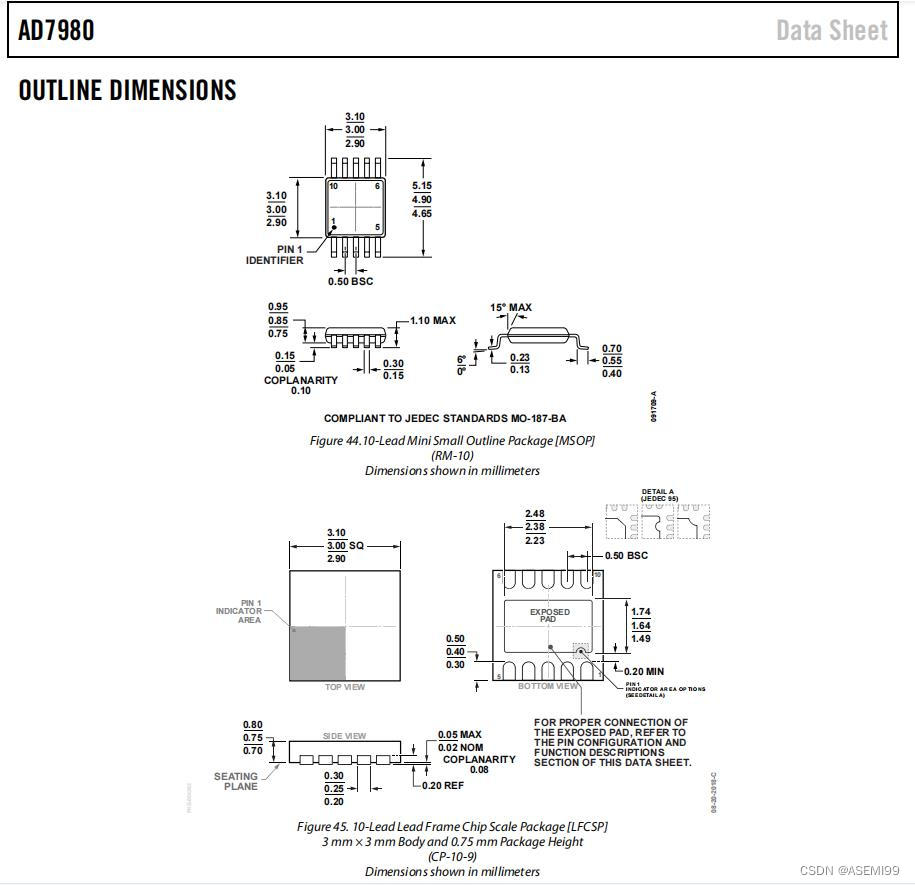
ASEMI代理AD7980BRMZRL7原装ADI(亚德诺)车规级AD7980BRMZRL7
编辑:ll ASEMI代理AD7980BRMZRL7原装ADI(亚德诺)车规级AD7980BRMZRL7 型号:AD7980BRMZRL7 品牌:ADI/亚德诺 封装:MSOP-10 批号:2023 安装类型:表面贴装型 AD7980BRMZRL7 汽车…...

leetcode141:环形链表
给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(…...
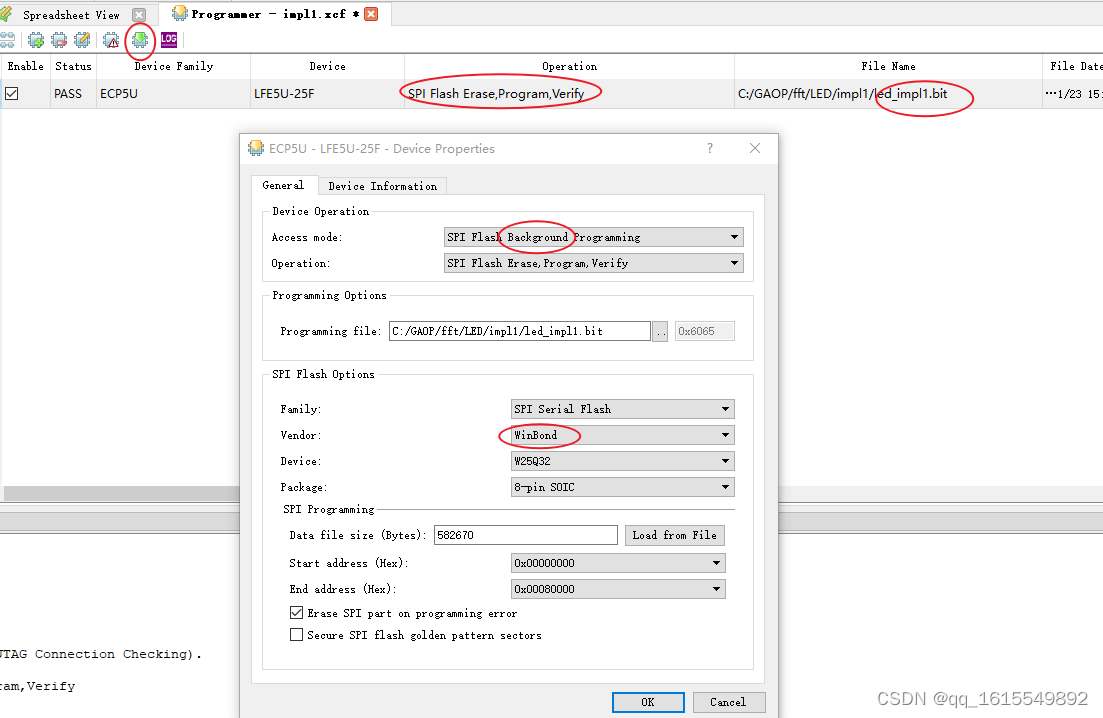
lattice diamond软件使用
1.diamond软件破解: lisence坚果云下载;或者这个博主操作环境变量设置: 2. 调用IP 有两种方式,依据芯片或者软件版本改变。 传统的IPexpress,每个IP单独例化。 新出的Clarity,多个IP在同一个顶层内调用…...

scala泛型
目录 类型参数 泛型函数: 协变,逆变,不变 泛型上下限: 上下文限定: 泛型是一种类型参数,该类型参数可以用在类、接口和方法中,分别被称为泛型类、泛型接口、泛型方法 类型参数 调用时不指定…...

程序员与ChatGPT的日常问答
程序员与ChatGPT的日常问答GPT3.5与GPT4.0能力对比技术问题工具问题编解码问题其他问题本文记录下调教ChatGPT的日常。 GPT3.5与GPT4.0能力对比 Q:采用同一个问题提问,对比下GPT3.5和GPT4.0的能力区别,比如:帮我列一个小白入门音频…...

如何创建高效的Prompt和ChatGPT等大语言模型AI对话
大语言模型,如OpenAI的GPT-4,是一种基于深度学习技术的自然语言处理工具,它可以理解自然语言并为用户提供有价值的回答。然而,要从大语言模型中获得高质量的回答,你需要学会如何高效地提问。本文将从原理出发ÿ…...

043:cesium加载Bing地图(多种形式)
第043个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中加载加载Bing地图。这里显示4种形式的地图,分别为:AERIAL、ROAD、CANVAS_DARK、AERIAL_WITH_LABELS。参考后面的API,还有其他几种形式。 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章…...

vscode代码片段生成
在刚学习vue的时候,有些代码片段是经常写的,在vscode中写一个代码片段可以帮助快速生成。 生成步骤: VSCode中的代码片段有固定的格式,所以我们一般会借助于一个在线工具来完成。 具体的步骤如下: 第一步,复制自己需…...

数据规整:聚合、合并和重塑
目录一、层次化索引重排与分级排序根据级别汇总统计二、合并数据集数据库风格的DataFrame合并索引上的合并轴向连接合并重叠数据三、重塑和轴向旋转重塑层次化索引将“长格式”旋转为“宽格式”将“宽格式”旋转为“长格式”一、层次化索引 层次化索引(hierarchica…...

开心档之C++ 信号处理
C 信号处理 目录 C 信号处理 signal() 函数 实例 raise() 函数 实例 信号是由操作系统传给进程的中断,会提早终止一个程序。在 UNIX、LINUX、Mac OS X 或 Windows 系统上,可以通过按 CtrlC 产生中断。 有些信号不能被程序捕获,但是下表…...

ChatGPT惨遭围剿?多国封杀、近万人联名抵制……
最近,全世界燃起一股围剿ChatGPT的势头。由马斯克、图灵奖得主Bengio等千人联名的“暂停高级AI研发”的公开信,目前签名数量已上升至9000多人。除了业内大佬,欧盟各国和白宫也纷纷出手。 最早“动手”的是意大利,直接在全国上下封…...
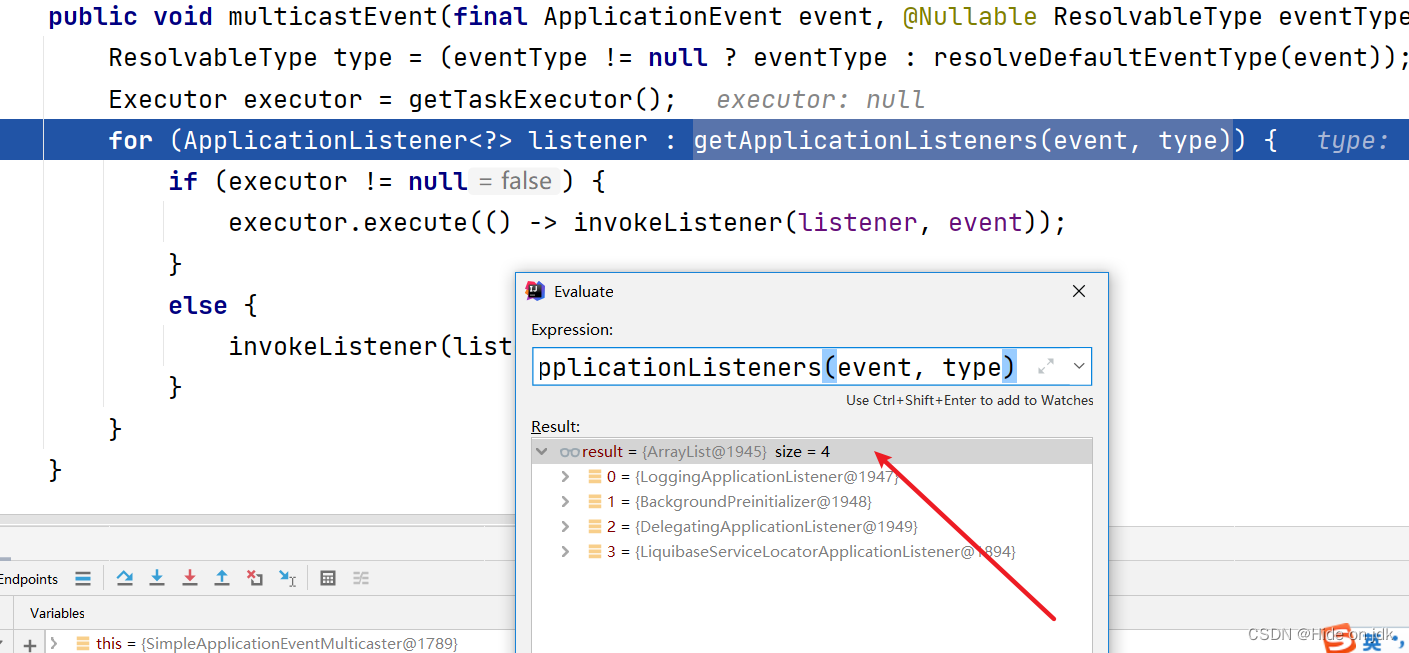
SpringBoot监听器
1.寻找spring.factories配置文件对应的监听器,主要要写监听器的全路径名,不然反射会报错 SpringBoot底层是如何读取META-INF/spring.factories的配置的? 1.遍历所有jar下的META-INF/spring.factories配置文件 2.读取配置文件下的所有属性&a…...

【网络安全】SQL注入--报错注入
报错注入报错注入定义代码展示常用的报错语句1.获取数据库名称2.获取mysql账号密码3.获取表名4.获取字段名5.获取账号密码报错注入定义 报错注入:利用sql语句的不规范,获取相关sql提示信息 代码展示 常用的报错语句 select first_name, last_name FROM…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
