【蓝桥杯】动态规划(dp)入门!| 入门动态规划的正确方式! ——学习笔记
目录
最暴力的dfs --> 记忆化搜索 ---> 递推(dp)
记忆化搜索 = 暴力dfs + 记录答案
递推的公式 = dfs 向下递归的公式
递推数组的初始值 = 递归的边界
动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibili 大佬教学视频,非常细!
题目一:大盗阿福
题目描述
输入格式输入的第一行是一个整数 T,表示一共有 T 组数据。接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。
输出格式对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
题目分析
题目代码1——最暴力的dfs
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式递推数组的初始值 = 递归的边界
题目代码4——递推(dp)
空间优化
第二题:数字三角形
输入格式
输出格式
输入输出样例
说明/提示
题目代码1——最暴力的dfs
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式递推数组的初始值 = 递归的边界
第三题:01背包问题
题目代码1——最暴力的dfs
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式递推数组的初始值 = 递归的边界
最暴力的dfs --> 记忆化搜索 ---> 递推(dp)
记忆化搜索 = 暴力dfs + 记录答案
递推的公式 = dfs 向下递归的公式
递推数组的初始值 = 递归的边界
动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibili 大佬教学视频,非常细!
题目一:大盗阿福
题目描述
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T 组数据。
接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。
第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。输出格式
对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。输入样例
2
3
1 8 2
4
10 7 6 14输出样例
8
24数据范围
T ≤ 50
1 ≤ N ≤ 105提示
对于第一组样例,阿福选择第 2 家店铺行窃,获得的现金数量为 8。
对于第二组样例,阿福选择第 1 和 4 家店铺行窃,获得的现金数量为 10 + 14 = 24。
题目分析
最暴力的dfs --> 记忆化搜索 ---> 递推(dp)
题目代码1——最暴力的dfs
import java.util.Arrays; import java.util.Scanner;public class 大盗阿福_dp {static int t, n;static int arr[] = new int[106];static int mem[] = new int[106];public static void main(String[] args) {Scanner sca = new Scanner(System.in);t = sca.nextInt();while (t-- > 0) {n = sca.nextInt();for (int i = 1; i <= n; i++) {arr[i] = sca.nextInt();}System.out.println(dfs(1));}}static int dfs(int x) {//x:表示当前正在考虑哪家店if (x > n) return 0;else return Math.max(dfs(x + 1), dfs(x + 2) + arr[x]);} }
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
import java.util.Arrays; import java.util.Scanner;public class 大盗阿福_dp {static int t, n;static int arr[] = new int[106];static int mem[] = new int[106];public static void main(String[] args) {Scanner sca = new Scanner(System.in);t = sca.nextInt();while (t-- > 0) {n = sca.nextInt();for (int i = 1; i <= n; i++) {arr[i] = sca.nextInt();}Arrays.fill(mem,0);//每一组记忆化前都要赋值为0System.out.println(dfs(1));}}//mem[i]存的是从第i家店铺开始(i~n)能洗劫到的最大价值static int dfs(int x) {if (mem[x] != 0) return mem[x];//记忆化搜索int sum = 0;if (x > n) sum = 0;else sum = Math.max(dfs(x + 1), dfs(x + 2) + arr[x]);mem[x] = sum;return sum;} }
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式
递推数组的初始值 = 递归的边界import java.util.Arrays; import java.util.Scanner;public class 大盗阿福_dp {static int t, n;static int arr[] = new int[106];static int mem[] = new int[106];public static void main(String[] args) {Scanner sca = new Scanner(System.in);t = sca.nextInt();while (t-- > 0) {n = sca.nextInt();for (int i = 1; i <= n; i++) {arr[i] = sca.nextInt();}for (int i = n; i > 0; i--) {mem[i] = Math.max(mem[i+1], mem[i+2] + arr[i]);}System.out.println(mem[1]);}} }
题目代码4——递推(dp)
空间优化
import java.util.Arrays; import java.util.Scanner;public class 大盗阿福_dp {static int t, n;static int arr[] = new int[106];static int mem[] = new int[106];public static void main(String[] args) {Scanner sca = new Scanner(System.in);t = sca.nextInt();while (t-- > 0) {n = sca.nextInt();for (int i = 1; i <= n; i++) {arr[i] = sca.nextInt();}int sum=0, temp1 = 0, temp2 = 0;for (int i = 1; i <=n; i++) {sum = Math.max(temp1, temp2 + arr[i]);temp2 = temp1;temp1 = sum;}System.out.println(sum);}} }
第二题:数字三角形
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
7 3 8 8 1 0 2 7 4 4 4 5 2 6 5在上面的样例中,从 7→3→8→7→5 的路径产生了最大
输入格式
第一个行一个正整数 r ,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式
单独的一行,包含那个可能得到的最大的和。
输入输出样例
输入 #1复制
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5输出 #1复制
30说明/提示
【数据范围】
对于 100% 的数据,1≤r≤1000,所有输入在[0,100] 范围内。
题目代码1——最暴力的dfs
import java.util.Scanner;public class 数字三角形_dp1 {static int n;static int map[][];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();map = new int[n + 1][n + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {map[i][j] = sca.nextInt();}}System.out.println(dfs(1, 1));}static int dfs(int x, int y) {if (x > n || y > n) return 0;else return Math.max(dfs(x + 1, y), dfs(x + 1, y + 1)) + map[x][y];} }
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
import java.util.Scanner;public class 数字三角形_dp1 {static int n;static int map[][];static int mem[][];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();map = new int[1005][1005];mem = new int[1005][1005];for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {map[i][j] = sca.nextInt();}}System.out.println(dfs(1, 1));}static int dfs(int x, int y) {if (mem[x][y] > 0) return mem[x][y];int sum = 0;if (x > n || y > n) sum = 0;else sum = Math.max(dfs(x + 1, y), dfs(x + 1, y + 1)) + map[x][y];mem[x][y] = sum;return sum;} }
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式
递推数组的初始值 = 递归的边界import java.util.Scanner;public class 数字三角形_dp2 {static int n;static int map[][];static int dp[][];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();map = new int[1005][1005];dp = new int[1005][1005];for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {map[i][j] = sca.nextInt();}}for (int i = n; i >= 1; i--) {//反着推for (int j = 1; j <= n; j++) {//j是从1开始dp[i][j] = Math.max(dp[i + 1][j], dp[i + 1][j + 1]) + map[i][j];}}System.out.println(dp[1][1]);} }
第三题:01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
8
题目代码1——最暴力的dfs
import java.util.Scanner;public class _01背包问题_dp1 {static int n, m,res=0;static int v[] = new int[1005];static int w[] = new int[1005];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();m = sca.nextInt();for (int i = 1; i <= n; i++) {v[i] = sca.nextInt();w[i] = sca.nextInt();}res = dfs(1, m);System.out.println(res);}static int dfs(int x, int spV) {//x表示当前考虑第几个物品,spV表示当前剩余的背包体积if (x > n) return 0;//剩余背包体积不够放当前物品时只能不选,考虑下一个物品if (spV < v[x]) return dfs(x + 1, spV);else if (spV >= v[x]) {//当背包剩余体积 > 当前物品体积时 有俩种选择 选/不选return Math.max(dfs(x + 1, spV), dfs(x + 1, spV - v[x]) + w[x]);}return 0;}}
题目代码 2——记忆化搜索模板
记忆化搜索 = 暴力dfs + 记录答案
import java.util.Scanner;public class _01背包问题_dp2 {static int n, m, res = 0;static int v[] = new int[1005];static int w[] = new int[1005];static int mem[][] = new int[1005][1005];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();m = sca.nextInt();for (int i = 1; i <= n; i++) {v[i] = sca.nextInt();w[i] = sca.nextInt();}res = dfs(1, m);System.out.println(res);}static int dfs(int x, int spV) {//x表示当前考虑第几个物品,spV表示当前剩余的背包体积if (mem[x][spV] != 0) return mem[x][spV];int sum = 0;if (x > n) sum = 0;//剩余背包体积不够放当前物品时只能不选,考虑下一个物品else if (spV < v[x]) sum = dfs(x + 1, spV);else if (spV >= v[x]) {//当背包剩余体积 > 当前物品体积时 有俩种选择 选/不选sum = Math.max(dfs(x + 1, spV), dfs(x + 1, spV - v[x]) + w[x]);}mem[x][spV] = sum;return sum;} }
题目代码3——递推(dp)
递推的公式 = dfs 向下递归的公式
递推数组的初始值 = 递归的边界import java.util.Scanner;public class _01背包问题_dp3 {static int n, m, res = 0;static int v[] = new int[1005];static int w[] = new int[1005];static int dp[][] = new int[1005][1005];public static void main(String[] args) {Scanner sca = new Scanner(System.in);n = sca.nextInt();m = sca.nextInt();for (int i = 1; i <= n; i++) {v[i] = sca.nextInt();w[i] = sca.nextInt();}//从下往上推for (int i = n; i >= 1; i--) {//i代表背包for (int j = 0; j <= m; j++) {//j代码背包体积if (j < v[i]) {//如果背包不够装dp[i][j] = dp[i + 1][j];} else if (j >= v[i]) {dp[i][j] = Math.max(dp[i + 1][j], dp[i + 1][j - v[i]] + w[i]);}}}System.out.println(dp[1][m]);} }
相关文章:
入门!| 入门动态规划的正确方式! ——学习笔记)
【蓝桥杯】动态规划(dp)入门!| 入门动态规划的正确方式! ——学习笔记
目录 最暴力的dfs --> 记忆化搜索 ---> 递推(dp) 记忆化搜索 暴力dfs 记录答案 递推的公式 dfs 向下递归的公式 递推数组的初始值 递归的边界 动态规划(dp)入门 | 这tm才是入门动态规划的正确方式! | dfs记忆化搜索 | 全体起立!!_哔哩哔哩_bilibili 大佬教学视频…...

元宇宙与网络安全
元宇宙是一种虚拟现实空间,用户可以在计算机生成的环境中进行互动。元宇宙的应用范围很广,比如房地产,医疗,教育,军事,游戏等等。它提供了更具沉浸感的体验,更好地现实生活整合,以及…...

Pod控制器之hpa
简述 HPA全称HorizontalPodAutoscaler Pod水平自动扩缩容,Kubernetes控制器HPA是一种用于自动调整Pod数量的控制器。它可以根据资源使用情况自动增加或减少Pod的数量,以确保应用程序的高可用性和性能。HPA可以根据CPU使用率或自定义指标来进行调整&…...

发现一个白嫖GPT4.0的方法!真的是完胜3.5!
大家好,我是五竹。 先说个基本的科普,最近被问的人都嘛了。 1、ChatGPT账号只有两种:普通账号和plus账号。 2、普通账号升级到plus账号,需要绑定国外的支付方式,每个月大概130左右!plus账号更稳!更快&am…...
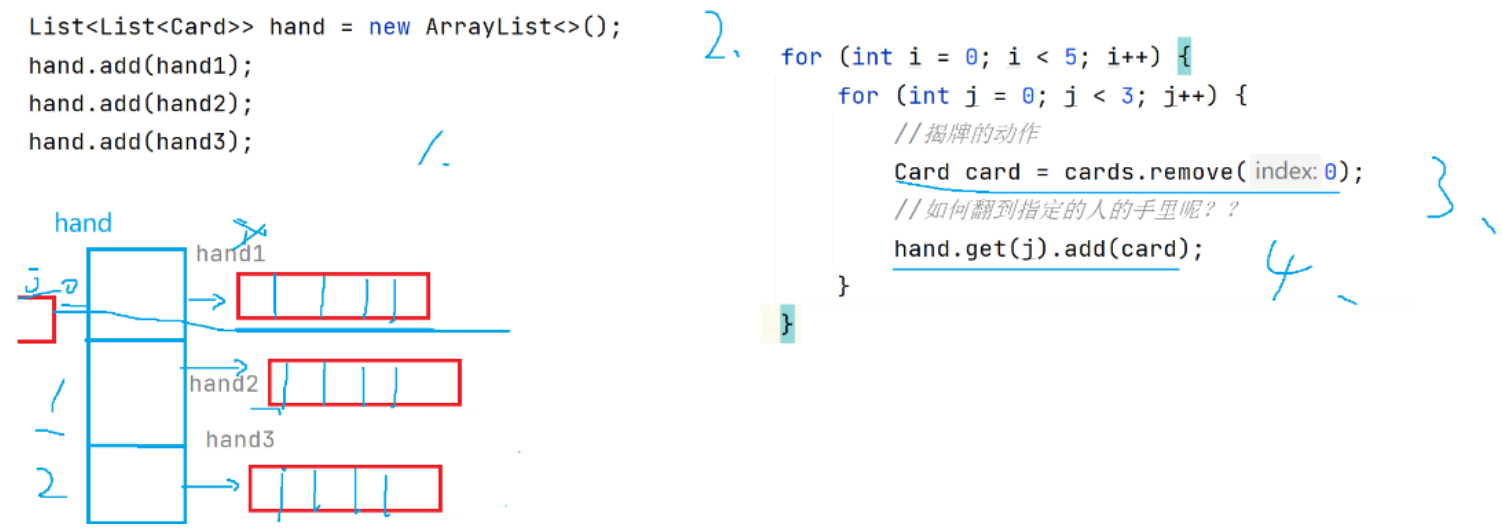
数据结构之第四章、ArrayList和顺序表
一、线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列... 线性表在逻辑上是线性结构,也就说是连续的一条直线。但是…...
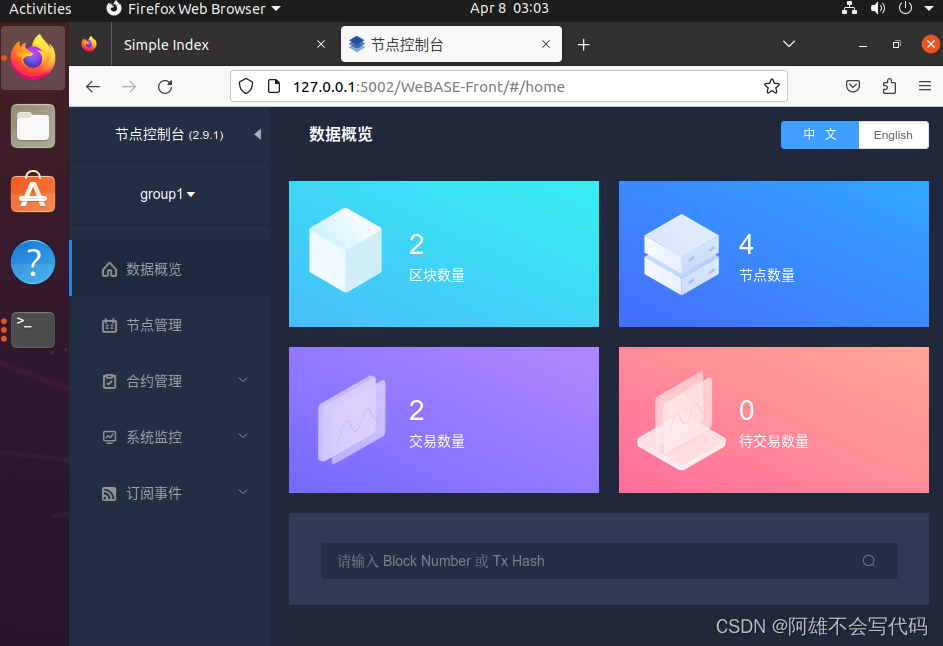
webase全家桶搭建教程过程记录+bug解决
前置条件 Ubuntu20 基础环境搭建 检查Java java -version 检查mysql(Ubuntu部署MySQL) mysql --version 在装MySQL的时候发现了一个问题 就是不管怎么sudo mysql_secure_installation,,第二步设置密码就是不对,解…...

openEuler Linux 部署 HadoopHA
openEuler Linux 部署 HadoopHA 升级操作系统和软件 yum -y update升级后建议重启 安装常用软件 yum -y install gcc gcc-c autoconf automake cmake make rsync vim man zip unzip net-tools zlib zlib-devel openssl openssl-devel pcre-devel tcpdump lrzsz tar wget修改…...
)
React-Hooks----useEffect()
文章目录前言用法前言 useEffect() 是 React 中最常用的 Hook 之一,它可以让函数组件拥有类似于类组件中 componentDidMount、componentDidUpdate 和 componentWillUnmount 生命周期函数的功能。 用法 useEffect() 接受两个参数 第一个参数是一个函数,…...

JavaWeb基础-汇总
SSM框架课程汇总01-MySQL基础02-MySQL高级03-JDBC04-JDBC练习05-Maven&Mybatis基础06-Mybatis练习07-JavaScript08-Web概述09-HTTP10-Tomcat11-Servlet12-Request&Response13-用户注册登录案例14-JSP15-JSP案例16-会话技术17-用户登录注册案例18-Filter19-Listener&…...

Niuke:JZ36.二叉树与双向链表
文章目录Niuke:JZ36.二叉树与双向链表题目描述示例思路分析代码实现Niuke:JZ36.二叉树与双向链表 题目描述 描述 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示 注意: 1.要求不能创建任何新的结点,只…...

javaScript---读懂promise、async/await
一、Promise Promise 是一个 Es 6 提供的类,目的是更加优雅地书写复杂的异步任务。可以解决嵌套式的回调地域问题,Promise 将嵌套格式的代码变成了顺序格式的代码。 //回调地域 setTimeout(function () {console.log("红灯");setTimeout(function () {console.lo…...
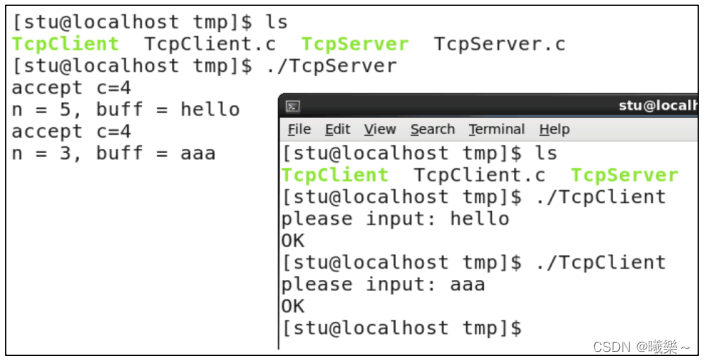
【Linux】TCP编程流程
TCP编程流程 socket()创建套接字,套接字TCP协议选择流式服务SOCK_STREAM。 bind()指定套接字使用的IP地址和端口。IP地址是自己主机地址,端口为一个16位的整形值。 listen()方法创建监听队列。监听队列分为存放未完成三次握手的连接和完成三次握手的连…...
SuperMap iDesktop 下载安装,生成本地瓦片,以及发布本地瓦片服务
SuperMap iDesktop 是插件式桌面GIS软件,提供基础版、标准版、专业版和高级版四个版本,具备二三维一体化的数据处理、制图、分析、海图、二三维标绘等功能,支持对在线地图服务的无缝访问及云端资源的协同共享,可用于空间数据的生产…...

【ONE·Data || 常见排序说明】
总言 数据结构基础:排序相关内容。 文章目录总言1、基本介绍2、插入排序2.1、直接插入排序:InsertSort2.1.1、单趟2.1.2、总趟2.2、希尔排序(缩小增量排序):ShellSort2.2.1、预排序1.0:单组分别排序2.…...

本节作业之跟随鼠标的天使、模拟京东按键输入内容、模拟京东快递单号查询
本节作业之跟随鼠标的天使、模拟京东按键输入内容、模拟京东快递单号查询1 跟随鼠标的天使2 模拟京东按键输入内容3 模拟京东快递单号查询1 跟随鼠标的天使 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><met…...

ChatGPT 被大面积封号,到底发生什么了?
意大利数据保护机表示 OpenAI 公司不但非法收集大量意大利用户个人数据,没有设立检查 ChatGPT 用户年龄的机制。 ChatGPT 似乎正在遭遇一场滑铁卢。 3月31日, 大量用户在社交平台吐槽,自己花钱开通的 ChatGPT 账户已经无法登录,更…...

教你精通JavaSE语法之第十一章、认识异常
一、异常的概念与体系结构 1.1异常的概念 在Java中,将程序执行过程中发生的不正常行为称为异常。比如之前写代码时经常遇到的: 1.算术异常 System.out.println(10 / 0); // 执行结果 Exception in thread "main" java.lang.ArithmeticExcep…...

display、visibility、opacity隐藏元素的区别
display、visibility、opacity隐藏元素的区别 display: none 事件监听:无法进行DOM事件监听。 元素从网页中消失,并且不占据位置再次从网页中出现会引起重排 进而引起重绘继承:不会被子元素继承,因为子元素也不被渲染。 visib…...

Linux Shell 实现一键部署tomcat10+java13
tomcat 前言 Tomcat 服务器是一个免费的开放源代码的Web 应用服务器,属于轻量级应用服务器,在中小型系统和并发访问用户不是很多的场合下被普遍使用,是开发和调试JSP 程序的首选。对于一个初学者来说,可以这样认为,当…...

软硬皆施,WMS仓库管理系统+PDA,实现效率狂飙
人工经验Excel表格,是传统第三方仓储企业常用的管理模式。在这种管理模式下,对仓库员工的Excel操作能力、业务经验和工作素养要求极高。一旦员工的经验能力不足,就会导致仓库业务运行不顺畅,效率低下,而员工也会因长时…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
