反常积分的审敛法
目录
无穷先的反常积分的审敛法
定理1:比较判别法
例题:
比较判别法的极限形式:
例题:
定理3:绝对收敛准则
例题:
无界函数的反常积分收敛法
例题:
无穷先的反常积分的审敛法
定理1:比较判别法

我们可以这样理解:

我们如何利用这个定理来求解题目呢?
我们可以拿要求解的反常积分和以下积分进行比较:
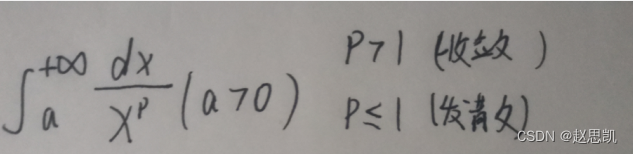
例题:
![]()
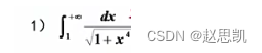
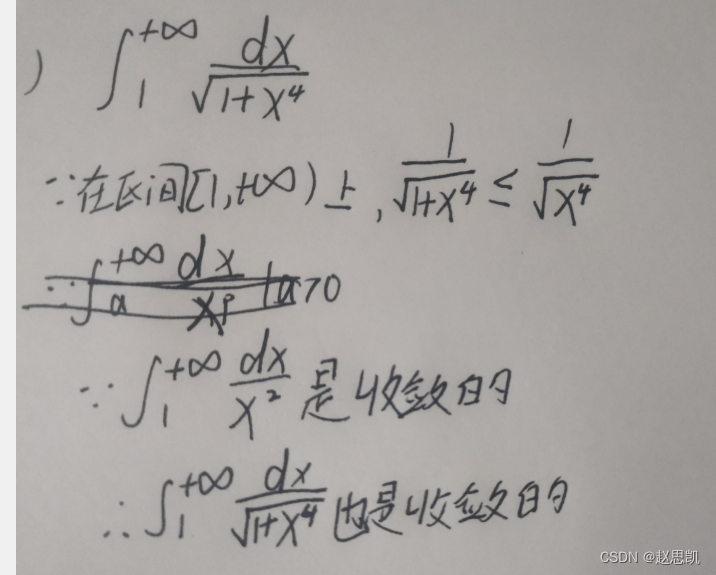
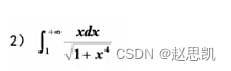

所以,在求解反常积分的敛散性时,我们需要提前在心里清楚这个积分的敛散性是怎么样的:
例如:

比较判别法的极限形式:

我们对第一条结论进行证明:

我们对剩下的两条进行说明:

如何利用这个定理求解问题呢?
例题:
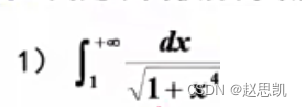

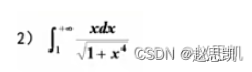

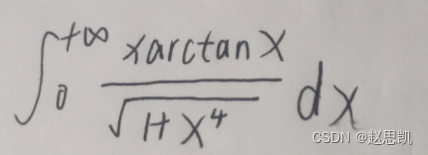

定理3:绝对收敛准则
例如:


我们进行证明:


例题:
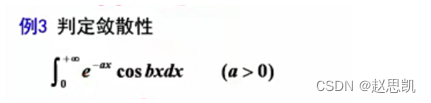
无界函数的反常积分收敛法
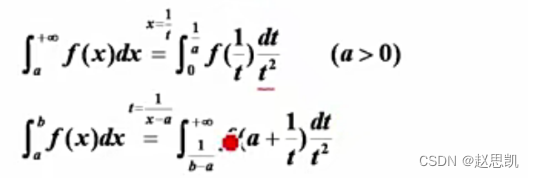
无穷区间的反常积分和无界函数的反常积分可以互相转换
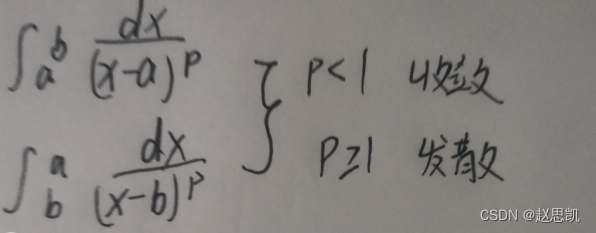
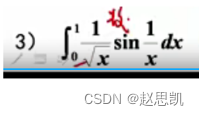
例题:


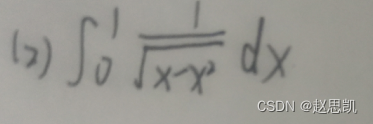


相关文章:

反常积分的审敛法
目录 无穷先的反常积分的审敛法 定理1:比较判别法 例题: 比较判别法的极限形式: 例题: 定理3:绝对收敛准则 例题: 无界函数的反常积分收敛法 例题: 无穷先的反常积分的审敛法 定理1&#x…...
(附python示例代码))
python实战应用讲解-【numpy专题篇】numpy常见函数使用示例(十三)(附python示例代码)
目录 Python numpy.ma.mask_or()函数 Python numpy.ma.notmasked_contiguous函数 Python numpy.ma.notmasked_edges()函数 Python numpy.ma.where()函数 Python Numpy MaskedArray.all()函数 Python Numpy MaskedArray.anom()函数 Python Numpy MaskedArray.any()函数 …...
—— 桥接模式)
Java设计模式(十九)—— 桥接模式
桥接模式定义如下:将抽象部分与它的实现部分分离,使它们都可以独立地变化。 适合桥接模式的情景如下: 不希望抽象和某些重要的实现代码是绑定关系,可运行时动态决定抽象和实现者都可以继承的方式独立的扩充,程序在运行…...

多线程并发安全问题
文章目录并发安全问题线程安全性死锁定义实现一个死锁查看死锁解决死锁其他线程安全问题单例模式并发安全问题 线程安全性 线程安全是指我们所写的代码在并发情况下使用时,总是能表现出正确的行为;反之,未实现线程安全的代码,表…...

P1005 [NOIP2007 提高组] 矩阵取数游戏
题目描述 帅帅经常跟同学玩一个矩阵取数游戏:对于一个给定的 ��nm 的矩阵,矩阵中的每个元素 ��,�ai,j 均为非负整数。游戏规则如下: 每次取数时须从每行各取走一个元素ÿ…...
百度云【人脸识别】
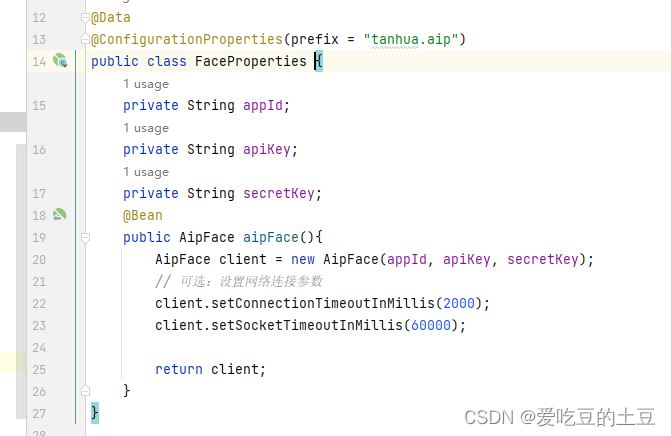
目录 1:百度云【人脸识别云服务】 2:Java-SDK文档 3:项目中测试 1:百度云【人脸识别云服务】 人脸识别云服务 包含实名认证、人脸对比、人脸搜索、活体检测等能力。灵活应用于金融、泛安防等行业场景,满足身份核验…...

强化模板模块
一、非类型模板参数 模板参数分为 类型模板参数(C模板的零基础讲解)和非类型模板参数。 看下面的代码 #define N 10 //T就是类型模板参数 template<class T> class Array { private:T a[N]; }; int main() {Array<int> a1;Array<double> a2;return 0; }上面…...
)
Vue.js学习详细课程系列--共32节(6 / 6)
Vue.js学习课程(6 / 6)29. 组件:参数验证知识点组件的数据综合例30. 组件:事件传递知识点v-on$emit综合例31. 组件:slot插槽知识点slot综合例32. 组件:组合slot知识点slot命名综合例29. 组件:参…...

【TFT屏幕】1.44寸彩屏
文章目录一.硬件层——引脚配置的移植二.应用层——显示函数的移植1. 移植显示一个字符函数2. 移植显示数字函数3.叠加方式选择一.硬件层——引脚配置的移植 宏定义的方式,直接修改引脚,实测可直接更改,非常方便移植 /*******************…...
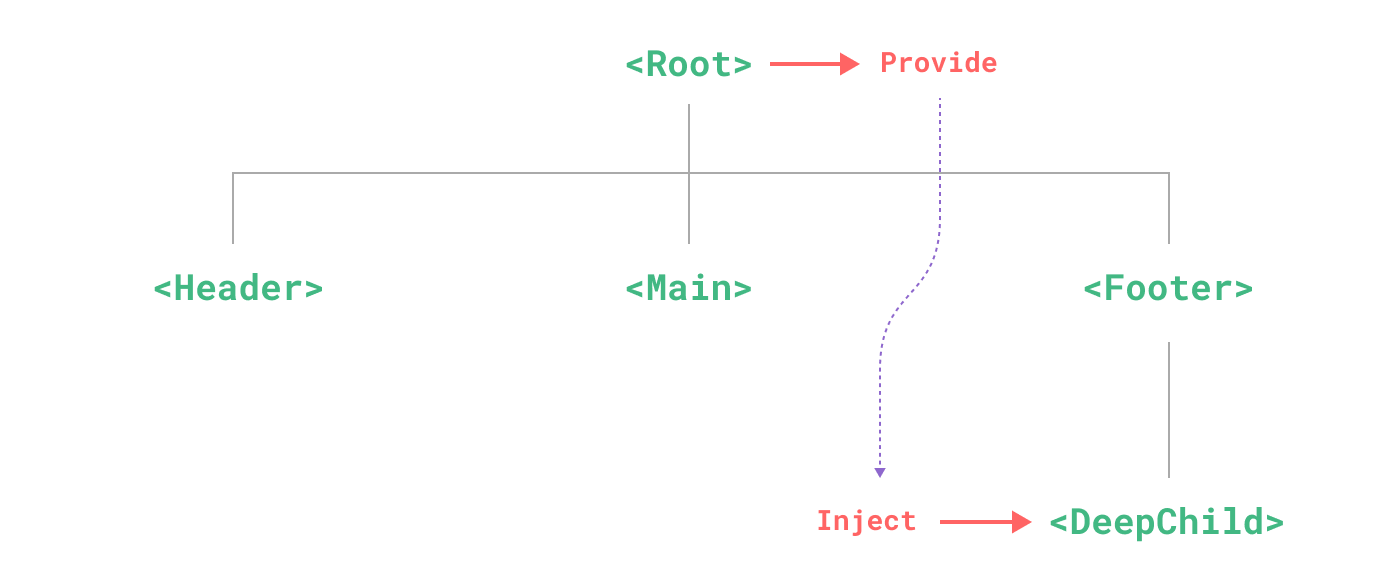
vue3组合式api
文章目录组合式API介绍什么是组合式 API?为什么要有组合式 API?更好的逻辑复用更灵活的代码组织Option ApiOption Api的缺陷Composition Api更好的类型推导更小的生产包体积与选项式 API 的关系取舍组合式 API 是否覆盖了所有场景?可以同时使…...
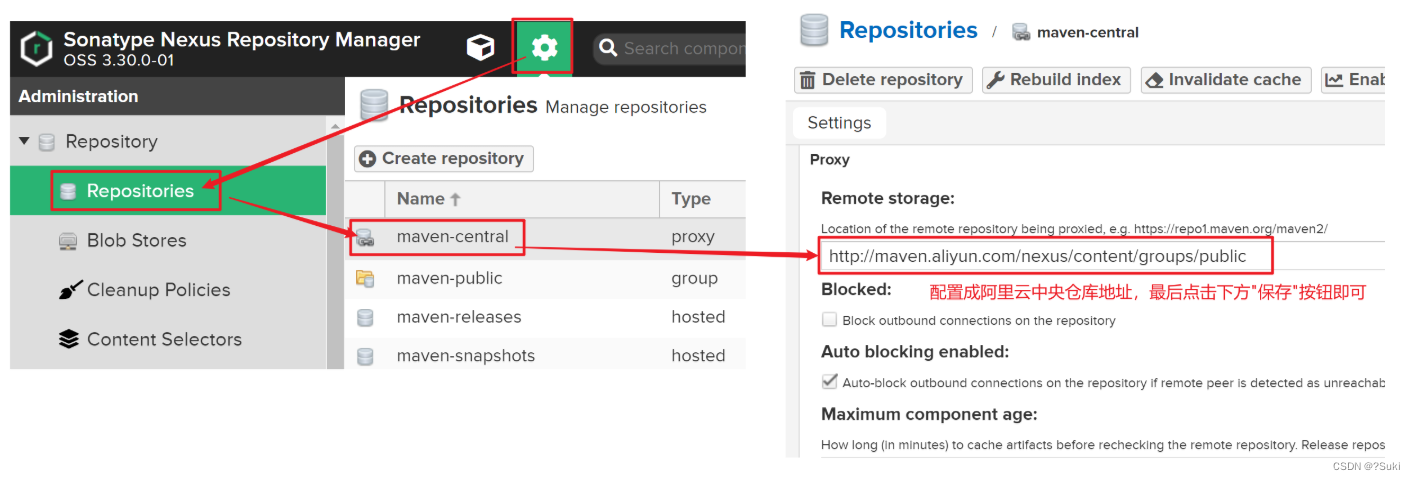
Maven高级-私服
Maven高级-私服6,私服6.1 私服简介6.2 私服安装步骤1:下载解压步骤2:启动Nexus步骤3:浏览器访问步骤4:首次登录重置密码6.3 私服仓库分类6.4 本地仓库访问私服配置步骤1:私服上配置仓库步骤2:配置本地Maven对私服的访问权限步骤3:配置私服的访问路径6.5 私服资源上传…...

网络优化小结
网络基础知识 OSI七层网络架构 OSI简称Open System Intercnnect,开放式系统互联,是一个国际互联网标准制定的一个组织 应用层 实际应用场景,比如 浏览器、文件传输、电子邮件、文件服务、虚拟终端等; http、FTP、ssh等 表示层…...

Android 11.0 原生SystemUI下拉通知栏UI背景设置为圆角背景的定制(一)
1.前言 在11.0的系统rom定制化开发中,在原生系统中关于SystemUI下拉状态栏的通知栏的每条通知的背景是白色的四角的背景, 由于在产品设计中,需要把四角背景默认改成白色的圆角背景,所以就需要分析系统原生下拉通知栏的每条通知的默认背景, 这就需要了解11.0的systemui的通…...

个人练习-Leetcode-1942. The Number of the Smallest Unoccupied Chair
题目链接:https://leetcode.cn/problems/the-number-of-the-smallest-unoccupied-chair/ 题目大意:给出一群人到达一个排队的时间和离开派对的时间[arr, lev]。有无数个座位,下标从0开始。当一个人在tm时刻离开时,如果一个人在tm…...
)
EMC经典问答85问(59-62问)
59、用双向可控硅控制直流电机的调速,但电机会干扰电源影响过零检则,造成不受控或速度妀变。请各位指教! 答 1: 出现这中现象的可能性有:1、电机属于非阻性负载,所以电路中产生相位移动,导致控制不准&#…...
Java面向对象 - 封装、继承和多态的综合练习(答案+知识点总结)第1关:封装、继承和多态进阶(一)+ 第2关:封装、继承和多态进阶(二)
目录 第1关:封装、继承和多态进阶(一) 报错总结 & 注意事项: 第2关:封装、继承和多态进阶(二) 源码: 报错总结 & 注意事项: 思维导图免费制作网站…...

小迪安全day20WEB漏洞-文件上传之基础及过滤方式
小迪安全day20WEB漏洞-文件上传之基础及过滤方式 什么是文件上传漏洞 有文件上传就可以测试是否有漏洞,关键看代码是否完备。 服务端代码未对客户端上传的文件进行严格的验证和过滤 漏洞危害 自定义网站后门,获取网站权限,属于高危漏洞。 上…...

LeetCode236.最近的公共祖先
求解最近公共祖先的算法 分为两个步骤: 求出两节点路径取两路径上最后一个相同的节点(该节点即为p,q节点的最近公共祖先) 节点路径的算法设计与实现 求节点路径即输入二叉树根节点与待求节点返回根节点到该节点路径上的所有节…...

【springcloud 微服务】Spring Cloud Alibaba整合Sentinel详解
目录 一、前言 二、环境准备 2.1 部署sentinel管控台 2.1.1 官网下载sentinel的jar包 2.1.2 启动控制台 2.1.3 访问控制台 2.2 整合springcloud-alibaba 2.2.1 引入相关依赖 2.2.2 修改配置文件 2.2.3 增加一个测试接口 2.2.4 接口测试 三、sentinel 流控规则使用 …...
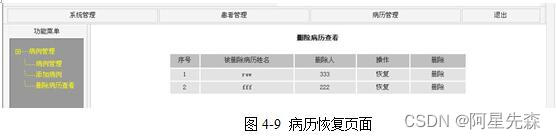
ASP医院管理系统—病历管理系统的设计与实现
病历管理系统是医院管理系统的重要组成,该系统的开发主要包括后台数据库的建立以及前台应用程序的开发两个方面。对于前者要求建立起数据一致性和完整性强、数据安全性好的数据库,而对于后者则要求具有齐全完善的应用程序功能,友好人性化的操作界面。该系统采用现代的办公自动化…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
