Chapter11.3:MATLAB_SIMULINK在离散系统中的应用
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍:《MATLAB/Simulink与控制系统仿真》。
3.MATLAB/SIMULINK在离散系统中的应用
3.1 MATLAB/SIMULINK在离散系统中常用函数
【连续系统模型与离散系统模型转换函数】
| 函数 | 调用格式 | 函数说明 |
|---|---|---|
| c2d{\rm c2d}c2d | sysd=c2d(sysc,Ts,′method′){\rm sysd=c2d(sysc,Ts,'method')}sysd=c2d(sysc,Ts,′method′) | 连续时间LTI{\rm LTI}LTI系统模型转换为离散时间系统模型 |
| d2c{\rm d2c}d2c | sysc=d2c(sysd,′method′){\rm sysc=d2c(sysd,'method')}sysc=d2c(sysd,′method′) | 离散时间LTI{\rm LTI}LTI系统模型转换为连续时间系统模型 |
| d2d{\rm d2d}d2d | sys=d2d(sysd,Ts){\rm sys=d2d(sysd,Ts)}sys=d2d(sysd,Ts) | 离散时间系统模型转换为新的Ts{\rm Ts}Ts离散时间系统模型 |
【method{\rm method}method功能说明】
| 选项 | 功能说明 | 选项 | 功能说明 |
|---|---|---|---|
| ′zoh′{\rm 'zoh'}′zoh′ | 对输入信号加零阶保持器 | ′tustin′{\rm 'tustin'}′tustin′ | 双线性变换方法 |
| ′foh′{\rm 'foh'}′foh′ | 对输入信号加一阶保持器 | ′prewarp′{\rm 'prewarp'}′prewarp′ | 预先转折变换方法,即改进的双线性变换方法 |
| ′imp′{\rm 'imp'}′imp′ | 脉冲不变变换方法 | ′matched′{\rm 'matched'}′matched′ | 零极点匹配变换方法 |
【离散系统时域响应函数】
| 函数名 | 调用格式 | 功能说明 |
|---|---|---|
| dstep{\rm dstep}dstep | dstep(dnum,dden,n)y=dstep(dnum,dden,n)\begin{aligned}&{\rm dstep(dnum,dden,n)}\\&{\rm y=dstep(dnum,dden,n)}\end{aligned}dstep(dnum,dden,n)y=dstep(dnum,dden,n) | 求离散系统单位阶跃响应 |
| dimpulse{\rm dimpulse}dimpulse | dimpulse(dnum,dden,n)y=dimpulse(dnum,dden,n)\begin{aligned}&{\rm dimpulse(dnum,dden,n)}\\&{\rm y=dimpulse(dnum,dden,n)}\end{aligned}dimpulse(dnum,dden,n)y=dimpulse(dnum,dden,n) | 求离散系统单位脉冲响应 |
| dlsim{\rm dlsim}dlsim | dlsim(dnum,dden,u)y=dlsim(dnum,dden,u)\begin{aligned}&{\rm dlsim(dnum,dden,u)}\\&{\rm y=dlsim(dnum,dden,u)}\end{aligned}dlsim(dnum,dden,u)y=dlsim(dnum,dden,u) | 求离散系统在输入u{\rm u}u下的响应 |
注:n{\rm n}n为采样次数,u{\rm u}u为输入函数;
【离散系统频域响应函数】
| 函数名 | 调用格式 | 功能说明 |
|---|---|---|
| dbode{\rm dbode}dbode | dbode(dnum,dden,Ts,w)[mag,phase,w]=dbode(dnum,dden,Ts,w)\begin{aligned}&{\rm dbode(dnum,dden,Ts,w)}\\&{\rm [mag,phase,w]=dbode(dnum,dden,Ts,w)}\end{aligned}dbode(dnum,dden,Ts,w)[mag,phase,w]=dbode(dnum,dden,Ts,w) | 离散Bode{\rm Bode}Bode图 |
| dnyquist{\rm dnyquist}dnyquist | dnyquist(dnum,dden,Ts,w)[re,im,w]=dnyquist(dnum,dden,Ts,w)\begin{aligned}&{\rm dnyquist(dnum,dden,Ts,w)}\\&{\rm [re,im,w]=dnyquist(dnum,dden,Ts,w)}\end{aligned}dnyquist(dnum,dden,Ts,w)[re,im,w]=dnyquist(dnum,dden,Ts,w) | 离散Nyquist{\rm Nyquist}Nyquist图 |
| dnichols{\rm dnichols}dnichols | dnichols(dnum,dden,Ts,w)[re,im,w]=dnichols(dnum,dden,Ts,w)\begin{aligned}&{\rm dnichols(dnum,dden,Ts,w)}\\&{\rm [re,im,w]=dnichols(dnum,dden,Ts,w)}\end{aligned}dnichols(dnum,dden,Ts,w)[re,im,w]=dnichols(dnum,dden,Ts,w) | 离散Nichols{\rm Nichols}Nichols图 |
| margin{\rm margin}margin | margin(dsys)[Gm,Pm,Wcg,Wcp]=margin(dsys)\begin{aligned}&{\rm margin(dsys)}\\&{\rm [Gm,Pm,Wcg,Wcp]=margin(dsys)}\end{aligned}margin(dsys)[Gm,Pm,Wcg,Wcp]=margin(dsys) | 离散Bode{\rm Bode}Bode图,显示频域性能参数 |
注:Ts{\rm Ts}Ts为采样周期,mag{\rm mag}mag为幅值向量,phase{\rm phase}phase为相交向量,Gm{\rm Gm}Gm为增益裕量,Pm{\rm Pm}Pm为相角裕量,re{\rm re}re为Nyquist{\rm Nyquist}Nyquist图或Nichols{\rm Nichols}Nichols图实部向量,im{\rm im}im为Nyquist{\rm Nyquist}Nyquist图或Nichols{\rm Nichols}Nichols图虚部向量;
3.2 实战部分
3.2.1 实战1
实验要求:已知一个连续线性系统如下图所示,其中:Gp(s)=1s(s+1)G_p(s)=\displaystyle\frac{1}{s(s+1)}Gp(s)=s(s+1)1,用零阶保持器方法、一阶保持器方法、双线性变换方法和根匹配方法将此连续系统离散化,其中采样周期为:Ts=0.1sT_s=0.1{\rm s}Ts=0.1s。

解:
% 实例Chapter11.3.2.1
clc;clear;num=[1];den=[1,1,0];G=tf(num,den); % 连续系统传递函数模型
Ts=0.1;Gd1=c2d(G,Ts,'zoh'); % 零阶保持器方法
Gd2=c2d(G,Ts,'foh'); % 一阶保持器方法
Gd3=c2d(G,Ts,'tustin'); % 双线性变换方法
Gd4=c2d(G,Ts,'matched'); % 零极点匹配方法Gd1,Gd2,Gd3,Gd4
% 结果显示:% 零阶保持器方法
Gd1 =0.004837 z + 0.004679----------------------z^2 - 1.905 z + 0.9048% 一阶保持器方法
Gd2 =0.001626 z^2 + 0.006344 z + 0.001547------------------------------------z^2 - 1.905 z + 0.9048% 双线性变换方法
Gd3 =0.002381 z^2 + 0.004762 z + 0.002381------------------------------------z^2 - 1.905 z + 0.9048% 零极点匹配变换方法
Gd4 =0.004761 z + 0.004761----------------------z^2 - 1.905 z + 0.9048
3.2.2 实战2
实验要求:已知一个连续系统如下图所示,其中:G1(s)=2s(s+30),G2(s)=10s2+6s+5G_1(s)=\displaystyle\frac{2}{s(s+30)},G_2(s)=\displaystyle\frac{10}{s^2+6s+5}G1(s)=s(s+30)2,G2(s)=s2+6s+510,采样周期Ts=0.1sT_s=0.1{\rm s}Ts=0.1s,求系统的脉冲闭环传递函数。

解:
% 实例Chapter11.3.2.2
clc;clear;Ts=0.1;
num1=[2];den1=[1,30,0];
num2=[10];den2=[1,6,5];G1=tf(num1,den1);
G2=tf(num2,den2);% 采用零阶保持器方法进行系统变换
G1d=c2d(G1,Ts);
G2d=c2d(G2,Ts);Gd=G1d*G2d;
GHd=feedback(Gd,1); % 闭环系统模型% 模型显示
G1d,G2d,GHd
% 结果显示:% G1的离散模型
G1d =0.004555 z + 0.00178----------------------z^2 - 1.05 z + 0.04979% G2的离散模型
G2d =0.04117 z + 0.03372----------------------z^2 - 1.511 z + 0.5488% 闭环离散模型
GHd =0.0001875 z^2 + 0.0002268 z + 6e-05------------------------------------------------z^4 - 2.561 z^3 + 2.185 z^2 - 0.6512 z + 0.02738
3.2.3 实战3
实验要求:使用MATLAB{\rm MATLAB}MATLAB绘制离散系统G(z)=2z2−3.4z+1.5z2−1.6z+0.8G(z)=\displaystyle\frac{2z^2-3.4z+1.5}{z^2-1.6z+0.8}G(z)=z2−1.6z+0.82z2−3.4z+1.5的带栅格线的根轨迹图。
解:
% 实例Chapter11.3.2.3
clc;clear;num=[2,-3.4,1.5];den=[1,-1.6,0.8];
zgrid('new');rlocus(num,den);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('离散系统的根轨迹图','FontSize',15);

3.2.4 实战4
实验要求:已知系统闭环传递函数为:G(z)=z3−1.3z2+1.22z+0.51z4+0.522z3+0.4z2+0.0086z−0.3915,T=0.5G(z)=\displaystyle\frac{z^3-1.3z^2+1.22z+0.51}{z^4+0.522z^3+0.4z^2+0.0086z-0.3915},T=0.5G(z)=z4+0.522z3+0.4z2+0.0086z−0.3915z3−1.3z2+1.22z+0.51,T=0.5,绘制此系统的零极点图,判断此系统的稳定性。
解:
% 实例Chapter11.3.2.4
clc;clear;% 建立系统模型
num=[1,-1.3,1.22,0.51];
den=[1,0.522,0.4,0.0086,-0.3915];
G=tf(num,den);% 绘制零极点图
pzmap(G);
axis([-1.2,1.2,-1.2,1.2]);axis equal;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('离散系统的零极点图','FontSize',15);

- 由零极点图可知,闭环传递函数所有极点都位于单位圆内部,闭环系统稳定;
3.2.5 实战5
实验要求:若某控制系统结构如下图所示,其中:D1(z)=3.4z−1−1.5z−21−1.6z−1+0.8z−2D_1(z)=\displaystyle\frac{3.4z^{-1}-1.5z^{-2}}{1-1.6z^{-1}+0.8z^{-2}}D1(z)=1−1.6z−1+0.8z−23.4z−1−1.5z−2,G1G_1G1是零阶保持器,G1(s)=1−e−0.05ss,G2(s)=0.25s2+3s+2G_1(s)=\displaystyle\frac{1-{\rm e}^{-0.05s}}{s},G_2(s)=\displaystyle\frac{0.25}{s^2+3s+2}G1(s)=s1−e−0.05s,G2(s)=s2+3s+20.25,采样周期:Ts=0.05sT_s=0.05{\rm s}Ts=0.05s,求系统开环和闭环的zzz传递函数,及sss传递函数,当输入为单位阶跃函数时,求其输出。

解:
【求系统开环和闭环sss传递函数】
% 实例Chapter11.3.2.5
clc;clear;% 系统开环和闭环s传递函数
dnum1=[3.4,-1.5];dden1=[1,-1.6,0.8];Ts=0.05;
sysd1=tf(dnum1,dden1,Ts); % D1的z传递函数模型
sysc1=d2c(sysd1,'zoh');num2=[0.25];den2=[1,3,2];sys2=tf(num2,den2);
sysc2=sysc1*sys2 % 开环传递函数
sysbc=feedback(sysc2,1) % 闭环传递函数[num,den]=tfdata(sysbc,'v'); % 提取闭环传递函数的分子和分母
p=roots(den)
% 结果显示:% 开环s传递函数
sysc2 =13.99 s + 216---------------------------------------------s^4 + 7.463 s^3 + 106.4 s^2 + 281.8 s + 181.9% 闭环s传递函数
sysbc =13.99 s + 216-------------------------------------------s^4 + 7.463 s^3 + 106.4 s^2 + 295.8 s + 398% 特征方程的根
% 由于特征方程的根均在s左半平面,因此,系统是稳定的。
p =-2.1667 + 9.1429i-2.1667 - 9.1429i-1.5647 + 1.4351i-1.5647 - 1.4351i
【求取系统开环和闭环zzz传递函数】
% 系统开环和闭环z传递函数
dnum1=[3.4,-1.5];dden1=[1,-1.6,0.8];Ts=0.05;
sysd1=tf(dnum1,dden1,Ts); % D1的z传递函数模型num2=[0.25];den2=[1,3,2];
sys2=tf(num2,den2);
sysd2=c2d(sys2,Ts,'zoh'); % G1和G2串联的z传递函数模型sysd=sysd1*sysd2 % 系统开环z传递函数
sysbd=feedback(sysd,1) % 系统闭环z传递函数[dnum,dden]=tfdata(sysbd,'v');
pd=roots(dden) % 闭环系统特征根t=0:0.05:5;
y=dstep(dnum,dden,101);
stem(t,y); % 棒图显示响应曲线
xlabel('t');ylabel('y');
grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统响应曲线','FontSize',15);
% 结果显示:% 开环z传递函数
sysd =0.001011 z^2 + 0.0005156 z - 0.0004242---------------------------------------------z^4 - 3.456 z^3 + 4.63 z^2 - 2.862 z + 0.6886% 闭环z传递函数
sysbd =0.001011 z^2 + 0.0005156 z - 0.0004242----------------------------------------------z^4 - 3.456 z^3 + 4.631 z^2 - 2.861 z + 0.6881% 特征方程的根
pd =0.8030 + 0.3935i0.8030 - 0.3935i0.9250 + 0.0697i0.9250 - 0.0697i

3.2.6 实战6
实验要求:某控制系统结构如下图所示,其中:D1(z)=3.4z−1−1.5z−21−1.6z−1+0.8z−2D_1(z)=\displaystyle\frac{3.4z^{-1}-1.5z^{-2}}{1-1.6z^{-1}+0.8z^{-2}}D1(z)=1−1.6z−1+0.8z−23.4z−1−1.5z−2,G1G_1G1是零阶保持器,G1(s)=1−e−0.05ss,G2(s)=0.25s2+3s+2G_1(s)=\displaystyle\frac{1-{\rm e}^{-0.05s}}{s},G_2(s)=\displaystyle\frac{0.25}{s^2+3s+2}G1(s)=s1−e−0.05s,G2(s)=s2+3s+20.25,采样周期:Ts=0.05sT_s=0.05{\rm s}Ts=0.05s,求系统频率特性参数,绘制系统的Bode{\rm Bode}Bode图、Nyquist{\rm Nyquist}Nyquist图和Nichols{\rm Nichols}Nichols图。

解:
% 实例Chapter11.3.2.6
clc;clear;% 系统开环和闭环s传递函数
dnum1=[3.4,-1.5];dden1=[1,-1.6,0.8];Ts=0.05;
sysd1=tf(dnum1,dden1,Ts); % D1的z传递函数模型num2=[0.25];den2=[1,3,2];sys2=tf(num2,den2);
sysd2=c2d(sys2,Ts,'zoh');
sysd=sysd1*sysd2 % 开环z传递函数[dnumc,ddenc]=tfdata(sysd,'v'); % 提取开环传递函数的零极点figure(1);
[Gm,Pm,Wcg,Wcp]=margin(sysd) % 求系统频率特性参数
margin(sysd);grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统margin图','FontSize',15);w=0.01:0.01:100;figure(2);
dnyquist(dnumc,ddenc,Ts,w);grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统nyquist图','FontSize',15);figure(3);
nichols(sysd);grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统nichols图','FontSize',15);
% 结果显示:% 控制系统开环模型
sysd =0.001011 z^2 + 0.0005156 z - 0.0004242---------------------------------------------z^4 - 3.456 z^3 + 4.63 z^2 - 2.862 z + 0.6886% 频率特性参数
Gm =10.8194Pm =133.7794Wcg =6.4303Wcp =0.5625
【控制系统Bode{\rm Bode}Bode图】

【控制系统Nyquist{\rm Nyquist}Nyquist图】

【控制系统Nichols{\rm Nichols}Nichols图】

3.3 综合实例
实验要求:给定单位负反馈离散控制系统,其采样周期为1s1{\rm s}1s,开环传递函数为:G(s)=s+1s2G(s)=\displaystyle\frac{s+1}{s^2}G(s)=s2s+1与零阶保持器ZOH{\rm ZOH}ZOH串联,开环增益为KKK。求闭环控制系统稳定的条件,且绘制KKK取不同值时闭环系统的阶跃响应曲线。
解:
【STEP1{\rm STEP1}STEP1:建立控制系统的数学模型】
% 实例Chapter11.3.3
clc;clear;% 建立控制系统模型
Ts=1;sys_K=1;
num=[1,1];den=[1,0,0];
sysc=tf(num,den); % 连续系统传递函数
sysd=c2d(sysc,Ts,'zoh'); % 离散系统传递函数
sys_open=sys_K*sysd % 系统的开环传递函数
% 系统开环传递函数
sys_open =1.5 z - 0.5-------------z^2 - 2 z + 1
【STEP2{\rm STEP2}STEP2:绘制系统的根轨迹】
% 绘制系统的根轨迹
figure(1);
rlocus(sysd);axis([-2,2,-1,1]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统根轨迹图','FontSize',15);% 验证临界稳定的K值
% K=2时是临界稳定值
sys_K=2;
figure(2);
margin(sys_K*sysd);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统margin图','FontSize',15);figure(3);
[dnum,dden]=tfdata(sys_K*sysd,'v');
dnyquist(dnum,dden,Ts);axis([-5,5,-2.5,2.5]);
grid on;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统Nyquist图','FontSize',15);
【控制系统根轨迹图】

【控制系统Bode{\rm Bode}Bode图】

【控制系统Nyquist{\rm Nyquist}Nyquist图】

【STEP3{\rm STEP3}STEP3:控制系统阶跃响应】
% 绘制不同K值的阶跃响应
sys_K=1;
figure(4);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=1时控制系统阶跃响应','FontSize',15);sys_K=2;
figure(5);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=2时控制系统阶跃响应','FontSize',15);sys_K=3;
figure(6);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=3时控制系统阶跃响应','FontSize',15);



- 当K=1K=1K=1时,闭环系统稳定,阶跃响应曲线收敛;
- 当K=2K=2K=2时,闭环系统临界稳定,阶跃响应曲线等幅振荡;
- 当K=3K=3K=3时,闭环系统不稳定,阶跃响应曲线发散;
【完整代码】
% 实例Chapter11.3.3
clc;clear;% 建立控制系统模型
Ts=1;sys_K=1;
num=[1,1];den=[1,0,0];
sysc=tf(num,den); % 连续系统传递函数
sysd=c2d(sysc,Ts,'zoh'); % 离散系统传递函数
sys_open=sys_K*sysd % 系统的开环传递函数% 绘制系统的根轨迹
figure(1);
rlocus(sysd);axis([-2,2,-1,1]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统根轨迹图','FontSize',15);% 验证临界稳定的K值
sys_K=2;
figure(2);
margin(sys_K*sysd);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统margin图','FontSize',15);figure(3);
[dnum,dden]=tfdata(sys_K*sysd,'v');
dnyquist(dnum,dden,Ts);axis([-5,5,-2.5,2.5]);
grid on;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统Nyquist图','FontSize',15);% 绘制不同K值的阶跃响应
sys_K=1;
figure(4);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=1时控制系统阶跃响应','FontSize',15);sys_K=2;
figure(5);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=2时控制系统阶跃响应','FontSize',15);sys_K=3;
figure(6);
sys_close=feedback(sys_K*sysd,1);
[dnumc,ddenc]=tfdata(sys_close,'v');
dstep(dnumc,ddenc,25);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('K=3时控制系统阶跃响应','FontSize',15);
=========================COMPLETE================================================={\rm COMPLETE}======================== =========================COMPLETE========================
相关文章:

Chapter11.3:MATLAB_SIMULINK在离散系统中的应用
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
过滤器Filter
什么是Filter? Filter表示过滤器,是JavaWeb三大组件(Servlet、FIlter、Listener)之一。过滤器可以把对资源的请求拦截下来,总而实现一些特殊的功能 使用过滤器后,要想访问web服务器上的资源,必须…...
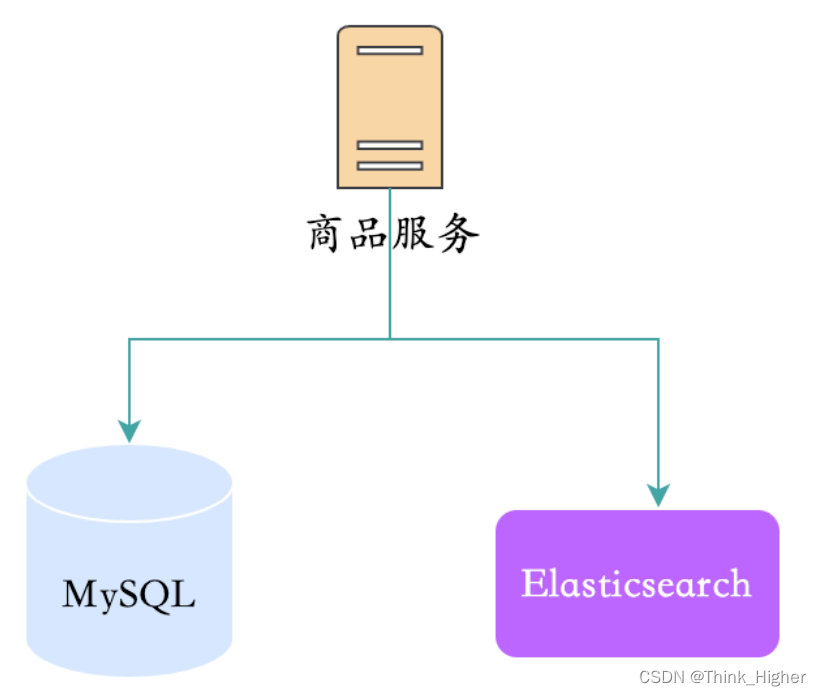
MySQL数据同步ES的常用思路和方法
文章目录 1.同步双写2.异步双写3.定时任务4.数据订阅大家应该都在各种电商网站检索过商品,检索商品一般都是通过什么实现呢?搜索引擎Elasticsearch。 那么问题来了,商品上架,数据一般写入到MySQL的数据库中,那么用于检索的数据又是怎么同步到Elasticsearch的呢? 1.同步双…...
spring源码之扫描前设置
扫描前设置 🛹源码源码说明总结启动一个springboot项目源码 org.springframework.context.annotation.ComponentScanAnnotationParser#parse public Set<BeanDefinitionHolder> parse(AnnotationAttributes componentScan, String declaringClass) {// 创建C…...

C++ 98/03 应该学习哪些知识19
迭代器、空间配置器理解 在 C 中,迭代器是一种可以用来遍历容器中的元素的对象。它们提供了一个类似于指针的接口,允许我们访问容器中的元素,而不必了解容器内部的结构。迭代器是 STL(标准模板库)的核心部分࿰…...
java毕业生就业信息管理系统servlet程序
1.系统登录:系统登录是用户访问系统的路口,设计了系统登录界面,包括用户名、密码和验证码,然后对登录进来的用户判断身份信息,判断是管理员用户还是普通用户。 2.系统用户管理:不管是…...

linux命令-netstat
linux命令-netstat 查看Linux中网络系统状态信息 补充说明 netstat命令 用来打印Linux中网络系统的状态信息,可让你得知整个Linux系统的网络情况。 语法 netstat(选项)选项 -a或--all:显示所有连线中的Socket; -A<网络类型>或--&…...
微服务+springcloud+springcloud alibaba学习笔记【Rest微服务工程搭建】(2/9)
Rest微服务工程搭建---学习笔记2/91、简单架构示意图2、创建Cloud-provider-payment8001 微服务提供者Module模块2.1. 建Module2.2. 改pom2.3. 写yml2.4. 主启动2.5. 业务类3、创建Cloud-consumer-order80 微服务消费者订单Module模块3.1. 建Module3.2. 改pom3.3. 写yml3.4. 主…...
【Redis7】Redis7 十大数据类型
【大家好,我是爱干饭的猿,本文重点介绍Redis7 十大数据类型。 后续会继续分享Redis7和其他重要知识点总结,如果喜欢这篇文章,点个赞👍,关注一下吧】 上一篇文章:《【Redis7】Redis7概述、安装…...

java 死锁怎么解决, 盘它
死锁归根结底还是资源的安排有问题如何使用 jps jstack,解决死锁如果是在分布式的系统中, 我该如何一步一步找到对应的堆栈解决死锁问题呢如何利用 skywalking 帮我解决死锁大多数人一辈子只做了三件事,自欺欺人被人欺 如何使用 jps jstack,解决死锁 jps和jstack都…...

【新2023Q2押题JAVA】华为OD机试 - 服务依赖
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:服务依赖 题目 在某系统中有…...
交友项目【通用设置】三个功能实现
目录 1:交友项目【通用设置】 1.1:查询通用设置 1.1.1:接口地址 1.1.2:流程分析 1.1.3:代码实现 1.2:设置陌生人问题 1.2.1:接口地址 1.2.2:流程分析 1.2.3:代码…...
MongoDB 更新文档(更新多条文档)
上一篇我们介绍了如何更新一条文档,本篇我们介绍一下,如果更新多条文档,我们来回顾一下更新多条文档的语法: db.collection.updateMany(filter, update, options) 上一篇我们对语法中的参数及参数的语法进行了详细的介绍…...

ubuntu20 qt6.4.3 ustc镜像安装 xdma
文件下载地质 命令 ./qt-unified-linux-x64-4.5.2-online.run --mirror https://mirrors.ustc.edu.cn/qtproject没有镜像就下砸错误hash verification while downloading,this is temporary error,please retry 部分安装器不支持 --mirror cd ~/workspace/dma_ip_drivers/X…...
15_I.MX6ULL_LCD显示原理
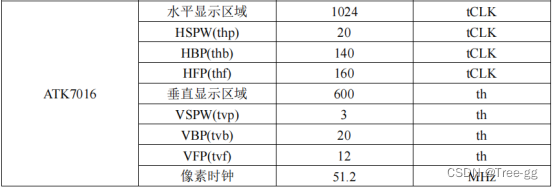
目录 LCD简介 分辨率 像素格式 LCD屏幕接口 LCD时间参数 RGB LCD屏幕时序 像素时钟 显存 LCD简介 LCD全称是Liquid Crystal Display,也就是液晶显示器,是现在最常用到的显示器,手机、电脑、各种人机交互设备等基本都用到了LCD,最常见就是手机和电脑显示器了。LCD的构造…...
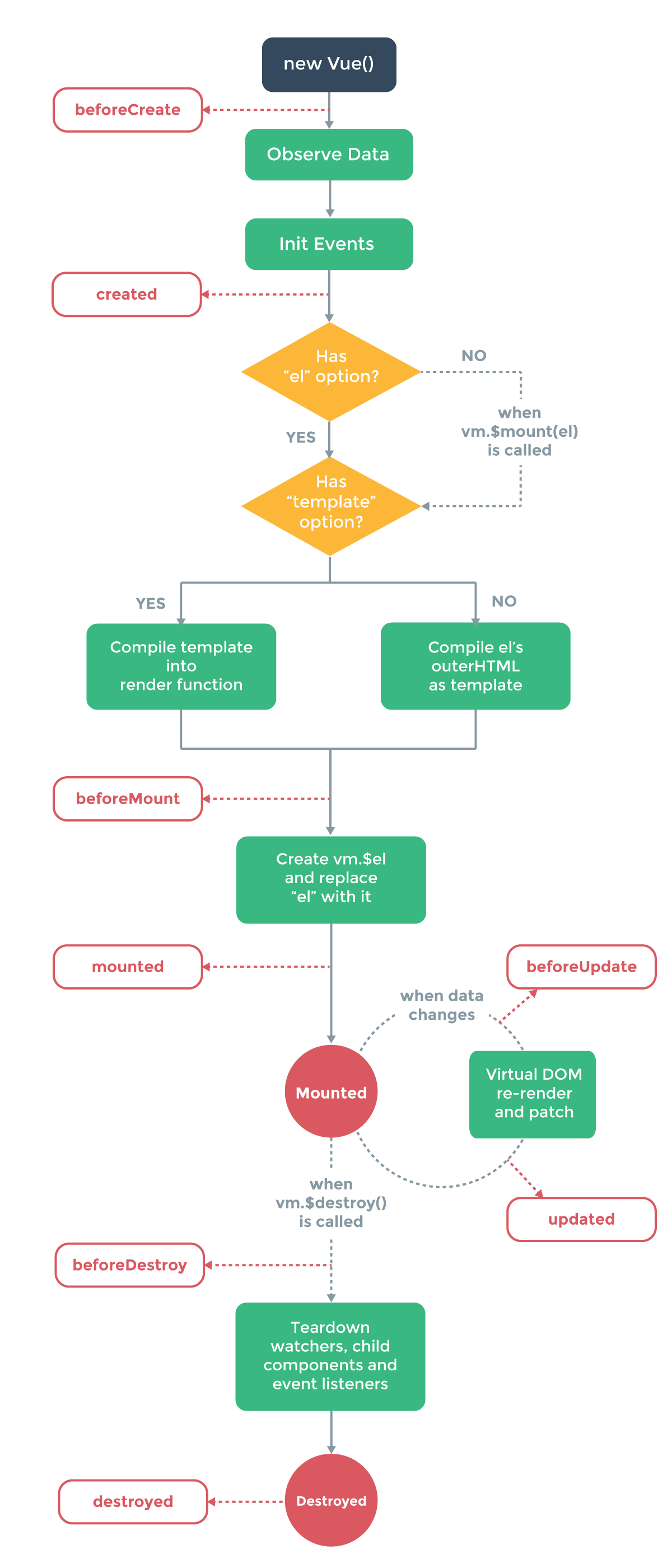
Vue.js 2.0 实例
构造器 每个 Vue.js 应用都是通过构造函数 Vue 创建一个 Vue 的根实例 启动的: var vm new Vue({// 选项 }) 虽然没有完全遵循 MVVM 模式, Vue 的设计无疑受到了它的启发。因此在文档中经常会使用 vm 这个变量名表示 Vue 实例。 在实例化 Vue 时&…...

安全技术和iptables防火墙
目录安全技术Netfilter防火墙工具介绍iptablesfirewalldnftablesiptables的组成概述netfilter与iptables关系iptables的四表五链结构介绍iptables安装iptables的命令格式数据包的常见控制类型iptables 命令常用管理选项添加规则删除规则修改规则 (不推荐使用&#x…...

StringBuilder和StringBuffer的区别
StringBuilder和StringBuffer的用法是一致的,平常我们最多用到的方法就是append()拼接字符串和reverse()翻转字符串等等。二者看起来方法是一样的,确实也是这样,其实它俩唯一的不同在于StringBuilder不是线程安全的,而StringBuffe…...
美团大数据开发转正实习面经(已OC)
一面面试体验整体很不错,面试官很温柔,也不会故意为难你。 一面(2023.3.21) 自我介绍简单介绍项目(研一在国电做的)你认为学习到的技术和实际使用的差距在哪项目中的数据都是哪里来的(集团中各种设备运行的数据)你说你用到了Spark那你介绍一下Spark的组件…...
leedcode刷题(2)
各位朋友们,又是新的一天,不知道大家过得怎样?今天是我leedcode刷题系列的第二篇,那么废话不多说,直接进入我们今天的主题。 文章目录有效的括号题目要求用例输入做题思路代码实现环形链表题目要求用例输入做题思路代码…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
