论文学习——VideoGPT
论文学习——VideoGPT: Video Generation using VQ-VAE and Transformers
原文链接:https://arxiv.org/abs/2104.10157
1. 设计思路
不同种类的生成模型在一下多个维度各有权衡:采样速度、样本多样性、样本质量、优化稳定性、计算需求、评估难易程度等等。
这些模型,除分数匹配模型(score-matching models)之外,广义上可以分为基于似然的模型(PixelCNNs, iGPT, NVAE, VQ-VAE, Glow)和对抗生成模型(GANs)。那么哪一类的模型适于研究和视频生成任务呢?
首先,从两大类模型中进行选择。基于似然的模型训练更为方便,因为目标是很容易理解的,在不同的batch size上都很容易优化,相对于GANs的判别器来讲,也十分易于评估。考虑到由于数据的性质,对视频任务建模已经是一个较大的挑战,因此我们任务基于似然的模型在优化和评估过程中存在的困难较少,因此可以关注于结构的改进上。
其次,在许多基于似然的模型中,我们选择了自回归模型,仅因为其在离散数据上运行良好,在样本质量上表现优异,且训练方法和模型架构上较为乘数,可以利用transformer中的最新改进。
在自回归模型中,考虑如下问题:自回归模型是在没有时空冗余的下采样潜空间内进行建模更好,还是在时空领域的所有帧、所有像素上训练好呢?考虑到自然视频的时空上的冗余度,作者选择了前者,通过将高维输入编码乘一个去噪后的下采样编码的方式去除冗余度。如在时空上进行4倍下采样,总分辨率就是64倍下采样,因此生成模型就能在更少更有用的信息上倾注计算量。如在VQ-VAE上,即使一个残缺的decoder也能将潜向量转化为足够真实的样本。并且在潜空间内建模也提升了计算速度。
上述三个原因促使VideoGPT的产生,这是一款使用基于似然的生成式模型,生成对象是自然视频。VideoGPT主体上有两个结构:VQ-VAE和GPT。
VQ-VAE中的autoencoder,通过3d卷积和轴向的注意力机制(axial self.attention)来从视频中学习其下采样潜空间的离散表征。
而类似于GPT的架构(强大的自回归先验)可以使用时空位置编码来为(VQ-VAE获得的)离散潜向量自回归地建模。
上述过程得到的潜向量再通过VQ-VAE的解码器,恢复为原像素规模的视频
后续在消融实验中,作者研究了axial attention blocks的优点、VQ-VAE潜空间大小、codebooks的输入、自回归先验的容量(模型大小)的影响。
2. 具体实现
VideoGPT的整体结构如下图所示:
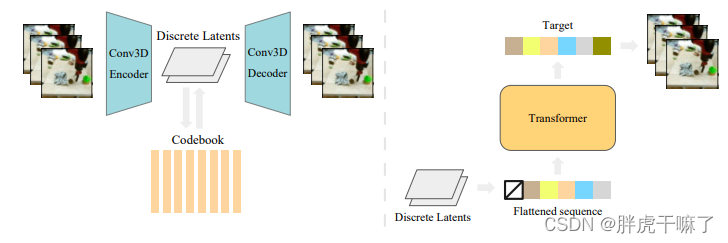
将模型分为两个部分进行讲解:
2.1 学习潜编码——VQ-VAE
为了学习到离散的latent code,首先在视频数据上训练VQ-VAE。编码器在时空维度使用3d卷积进行下采样,然后是残差注意力模块,该模块的结构如下所示,在模块中使用layernorm和轴向注意力机制。
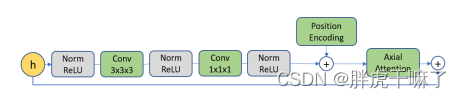
解码器的结构则是编码器的反向,先通过残差注意力模块,再通过3d转置卷积,在时空维度上进行上采样。位置编码是学习到的时间+空间上的嵌入,它们可以在encoder和decoder之间,所有轴向注意力层中共享。
关于VQ-VAE的轴向注意力,下面对其代码进行展示:
(1)需要注意的是VQ-VAE分为encoder和decoder,两部分对称。
class VQVAE(pl.LightningModule):def __init__(self, args):super().__init__()self.args = args# codebooks 中embedding的维度self.embedding_dim = args.embedding_dim# codebook中code 的数目self.n_codes = args.n_codes# n_hiddens: 残差块儿中隐藏特征的数目# n_res_layers: 残差块儿的数目# downsample: T, H, W三个维度下采样倍数self.encoder = Encoder(args.n_hiddens, args.n_res_layers, args.downsample)self.decoder = Decoder(args.n_hiddens, args.n_res_layers, args.downsample)(2)以encoder为例,其残差层数目n_res_layers取值为4,故而其self.res_stack部分共有4层
class Encoder(nn.Module):def __init__(self, n_hiddens, n_res_layers, downsample):super().__init__()n_times_downsample = np.array([int(math.log2(d)) for d in downsample])self.convs = nn.ModuleList()max_ds = n_times_downsample.max()for i in range(max_ds):in_channels = 3 if i == 0 else n_hiddensstride = tuple([2 if d > 0 else 1 for d in n_times_downsample])conv = SamePadConv3d(in_channels, n_hiddens, 4, stride=stride)self.convs.append(conv)n_times_downsample -= 1self.conv_last = SamePadConv3d(in_channels, n_hiddens, kernel_size=3)self.res_stack = nn.Sequential(*[AttentionResidualBlock(n_hiddens)for _ in range(n_res_layers)],nn.BatchNorm3d(n_hiddens),nn.ReLU())
(3)对于其中的每一层AttentionResidualBlock,即之前图中所提的残差注意力模块,模块的末端各对应一个AxialBlock,每个AxialBlock中对应时空三个维度的多头注意力机制
class AxialBlock(nn.Module):def __init__(self, n_hiddens, n_head):super().__init__()kwargs = dict(shape=(0,) * 3, dim_q=n_hiddens,dim_kv=n_hiddens, n_head=n_head,n_layer=1, causal=False, attn_type='axial')self.attn_w = MultiHeadAttention(attn_kwargs=dict(axial_dim=-2),**kwargs)self.attn_h = MultiHeadAttention(attn_kwargs=dict(axial_dim=-3),**kwargs)self.attn_t = MultiHeadAttention(attn_kwargs=dict(axial_dim=-4),**kwargs)
(4)对于每一个多头注意力,其注意力部分对应一个AxialAttention机制
class AxialAttention(nn.Module):def __init__(self, n_dim, axial_dim):super().__init__()# encoder 里4个attentionResidualBlock,对应4组axial-attention,每组3个# decoder 结构上与encoder对称,故也有4个attrntionResidualBlock# print(n_dim, axial_dim) # 如下内容,共8组,应该是共8个attention block# 3 -2# 3 -3# 3 -4if axial_dim < 0:axial_dim = 2 + n_dim + 1 + axial_dimelse:axial_dim += 2 # account for batch, head, dimself.axial_dim = axial_dimdef forward(self, q, k, v, decode_step, decode_idx):q = shift_dim(q, self.axial_dim, -2).flatten(end_dim=-3)k = shift_dim(k, self.axial_dim, -2).flatten(end_dim=-3)v = shift_dim(v, self.axial_dim, -2)old_shape = list(v.shape)v = v.flatten(end_dim=-3)# scaled dot-product attention,计算分类结果out = scaled_dot_product_attention(q, k, v, training=self.training)out = out.view(*old_shape)out = shift_dim(out, -2, self.axial_dim)return out
以上
2.2 学习到先验
模型的第二阶段是在VQ-VAE第一阶段的latent code的基础上学习一个先验。先验网络遵循Image-GPT的结构,另外还在feedforward layer和注意力块儿后面加入了dropout,以实现正则化。
以上过程是无条件限制的情况下进行训练的。可以通过训练带条件的先验(conditional prior)来生成conditional samples。条件限制有两种方法:
- 交叉注意力(Cross Attention):作为视频帧的限制,在先验网络的训练过程中,我们首先向3d的resnet中喂入有条件限制的帧,然后再resnet的输出上使用cross attention。
- 条件正则(Conditional Norms):与GANs中使用的限制方法相似,我们在transformer的Layer Normalization层上参数化gain和bias,作为条件张量(conditional vector)的放射函数。这种方法适用于对动作和类别进行限制的模型
相关文章:

论文学习——VideoGPT
论文学习——VideoGPT: Video Generation using VQ-VAE and Transformers 原文链接:https://arxiv.org/abs/2104.10157 1. 设计思路 不同种类的生成模型在一下多个维度各有权衡:采样速度、样本多样性、样本质量、优化稳定性、计算需求、评估难易程度等…...
底部导航详解)
Flutter系列(五)底部导航详解
Flutter系列(四)底部导航顶部导航图文列表完整代码,如下: Flutter系列(四)底部导航顶部导航图文列表完整代码_摸金青年v的博客-CSDN博客 目录 一、前言 二、Scaffold组件 三、BottomNavigationBar组件 …...
『pyqt5 从0基础开始项目实战』02. 页面布局设计(保姆级图文)
目录弹性布局介绍导包和框架代码布局框架搭建1. 总体布局框架2. 顶部菜单布局3. form添加内容布局4. table数据展示布局5. footer底部菜单完整项目代码总结欢迎关注 『pyqt5 从0基础开始项目实战』 专栏,持续更新中 欢迎关注 『pyqt5 从0基础开始项目实战』 专栏&am…...

【Python机器学习】——平均中位数模式
Python机器学习——平均中位数模式 文章目录 Python机器学习——平均中位数模式一、Python 平均中位数模式一、Python 平均中位数模式 均值、中值和众数 从一组数字中我们可以学到什么? 在机器学习(和数学)中,通常存在三中我们感兴趣的值: 均值(Mean) - 平均值 中值(M…...

Windows窗口
Windows窗口 Unit01注册窗口类 01窗口类的概念 窗口类是包括了窗口的各种参数信息的数据结构每个窗口都具有窗口类,基于窗口类创建窗口每个窗口都具有一个名称,使用前必须注册到系统 02窗口类的分类 系统窗口类 系统已经定义好的窗口类,…...
Spring Transaction 源码解读
Spring Transaction 规范的maven坐标如下: <dependency><groupId>org.springframework</groupId><artifactId>spring-tx</artifactId><version>...</version></dependency>该包提供了spring事务规范和默认的jta(ja…...
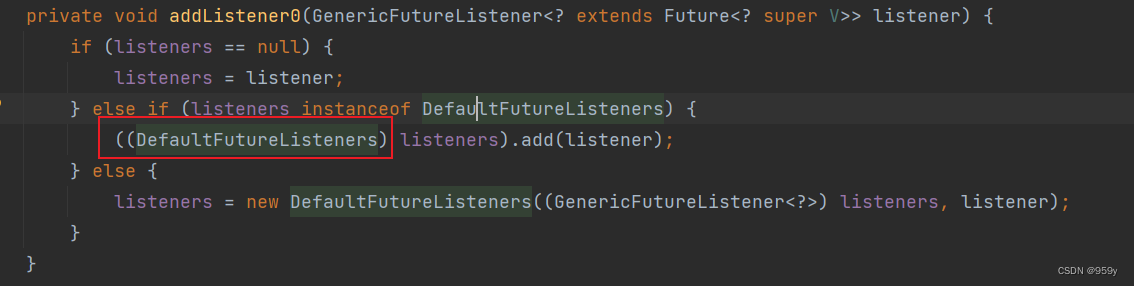
[Netty] Channel和ChannelFuture和ChannelFutureListener (六)
文章目录1.Channel介绍2.ChannelFuture接口介绍3.GenericFutureListener接口介绍1.Channel介绍 NIO的Channel与Netty的Channel 不一样 Netty重新设计了Channel接口,并且给予了很多不同的实现, Channel是Netty网络的抽象类, 除了NIO中Channel所包含的网络I/O操作, 主动建立和关…...

条件渲染
组件经常需要根据不同条件显示不同内容。在React中,你可以使用类似于if语句、&&和?:运算符的JavaScript语法有条件地呈现JSX。你将学到:如何根据条件返回不同的JSX如何有条件地包含或排除一段JSX在React代码库中常见的条件语法快捷方式有条件地…...
异步任务)
springboot(10)异步任务
文章目录1、SpringBoot异步任务1.1使用注解EnableAsync开启异步任务支持1.2使用Async注解标记要进行异步执行的方法1.3controller测试2.异步任务相关限制3.1自定义 Executor3.1.1应用层级:3.1.2方法层级:3.2自定义 Executor (第二种方式)4.1异常处理4.1.…...

清华大学开源的chatGLM-6B部署实战
Windows部署 win10 通过wsl部署 常见问题: torch.cuda.OutOfMemoryError: CUDA out of memory. 在Windows的系统环境变量中增加 变量名:PYTORCH_CUDA_ALLOC_CONF 变量值:max_split_size_mb:32 文档书写时使用3090 24G显存配置,其他规格酌情调整 32 至其他值,如未设置变…...

通过矩阵从整体角度搞懂快速傅里叶变换原理
离散傅里叶变换公式 公式 f[k]∑n0N−1g[n]e−i(2π/N)kn,其中(0<n<N)f[k]\sum_{n0}^{N-1}g[n]e^{-i(2\pi/N)kn}, 其中(0<n<N) f[k]n0∑N−1g[n]e−i(2π/N)kn,其中(0<n<N) 逆变换公式 g[n]1N∑k0N−1f[k]ei(2π/N)kn,其中(0<k<N)g[n]\frac{1}{N}\…...

【C++从0到1】25、C++中嵌套使用循环
C从0到1全系列教程 1、实例代码 #include <iostream> // 包含头文件。 using namespace std; // 指定缺省的命名空间。int main() {// 超女分4个小组,每个小组有3名超女,在控制台显示每个超女的小组编号和组内编号。// 用一个循环…...
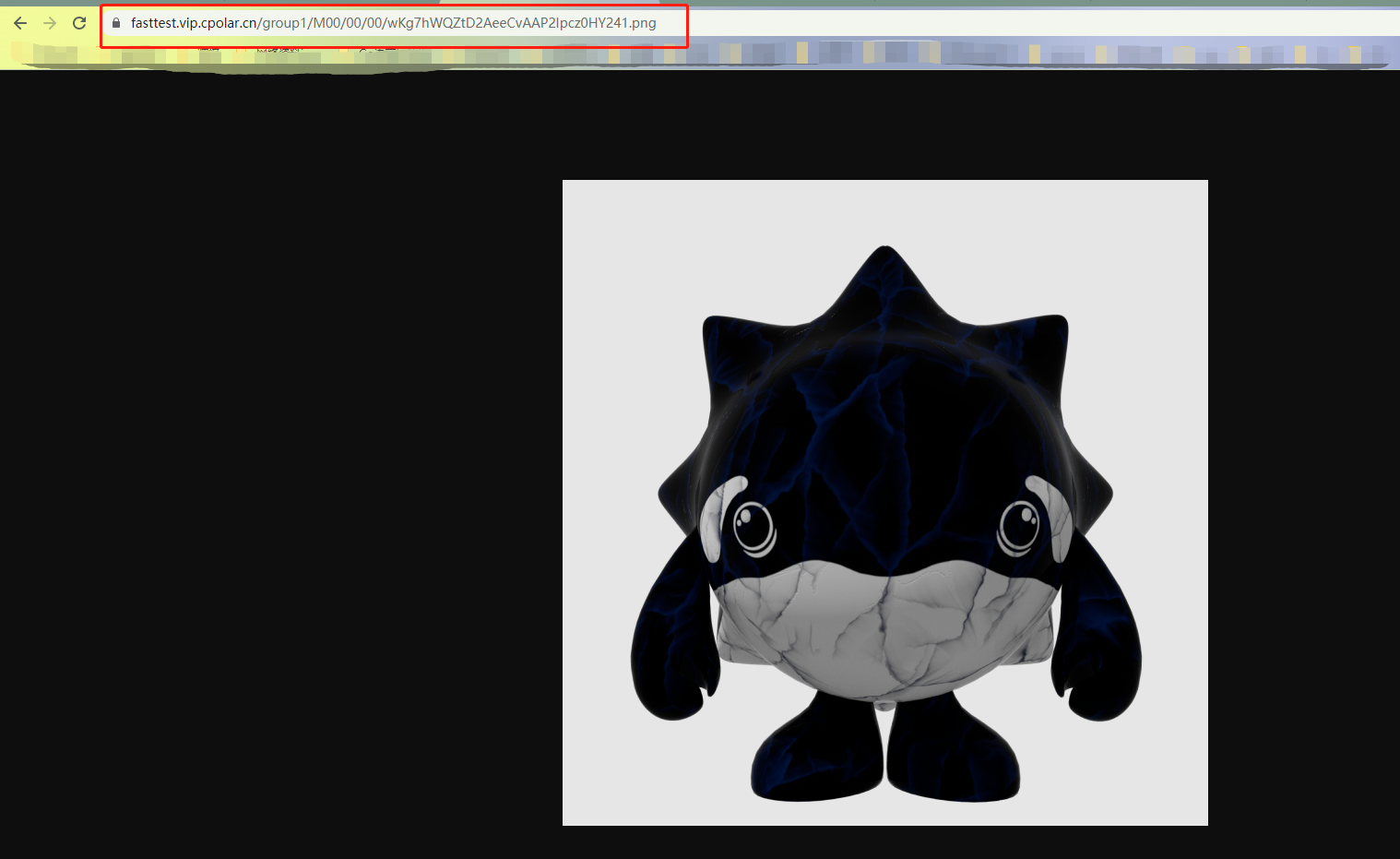
FastDFS与Nginx结合搭建文件服务器,并内网穿透实现公网访问
文章目录前言1. 本地搭建FastDFS文件系统1.1 环境安装1.2 安装libfastcommon1.3 安装FastDFS1.4 配置Tracker1.5 配置Storage1.6 测试上传下载1.7 与Nginx整合1.8 安装Nginx1.9 配置Nginx2. 局域网测试访问FastDFS3. 安装cpolar内网穿透4. 配置公网访问地址5. 固定公网地址5.1 …...
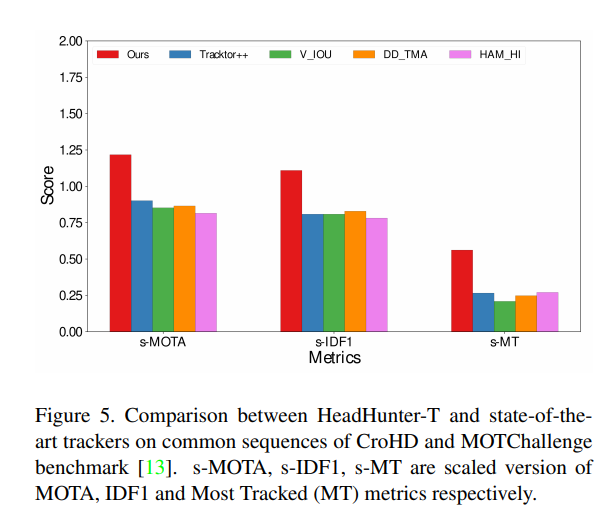
密集场景下的行人跟踪替代算法,头部跟踪算法 | CVPR 2021
一个不知名大学生,江湖人称菜狗 original author: Jacky LiEmail : 3435673055qq.com Time of completion:2023.4.8 Last edited: 2023.4.8 目录 摘要 主要内容 结果 这篇文章是CVPR 2021 的最新论文,文章的标题: 文章的主要内…...
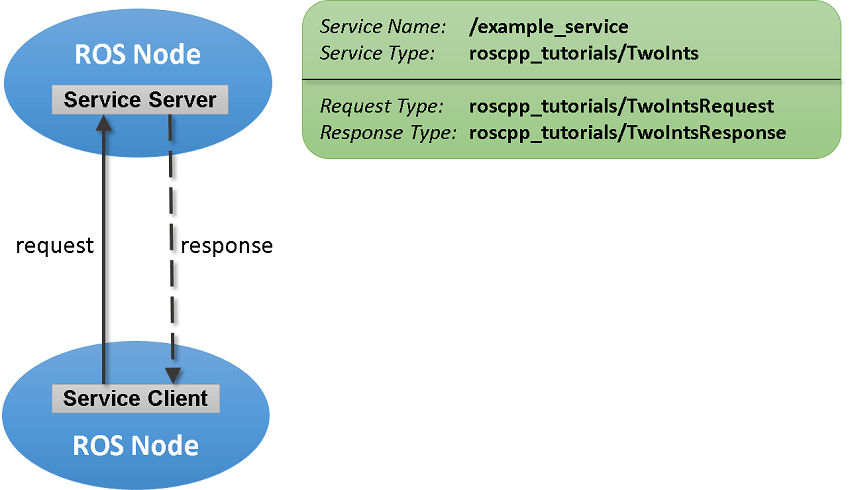
Matlab与ROS(1/2)---服务端和客户端数据通信(五)
0. 简介 在前几讲我们讲了Matlab中的Message以及Topic的相关知识。而ROS主要支持的通信机制还有服务这一类。服务通过允许请求以及响应的通信方式,来给整个系统完成更紧密的耦合。服务客户端向服务服务器发送请求消息并等待响应。服务器将使用请求中的数据构造响应…...

数字化转型的避坑指南:细说数字化转型十二大坑
随着信息技术的快速发展,数字化转型已经成为许多企业发展的必经之路。然而,数字化转型过程中也存在许多坑,如果不谨慎处理,就可能导致企业陷入困境。本文将细说数字化转型的十二大坑,并提供相应的避坑指南。 1、不了解…...

pt05Encapsulationinherit
Encapsulation &inherit 封装继承 封装 向类外提供必要的功能,隐藏实现的细节, 代码可读性更高优势:简化编程,使用者不必了解具体的实现细节,只需要调用对外提供的功能。私有成员:作用:无需向类外提供…...

面向对象编程(基础)9:封装性(encapsulation)
目录 9.1 为什么需要封装? 而“高内聚,低耦合”的体现之一: 9.2 何为封装性? 9.3 Java如何实现数据封装 9.4 封装性的体现 9.4.1 成员变量/属性私有化 实现步骤: 成员变量封装的好处: 9.4.2 私有化…...

fate-serving-server增加取数逻辑并源码编译
1.什么是fate-serving-server? FATE-Serving 是一个高性能、工业化的联邦学习模型服务系统,专为生产环境而设计,主要用于在线推理。 2.fate-serving-server源码编译 下载fate-serving-serving项目(GitHub - FederatedAI/FATE-Serving: A scalable, h…...
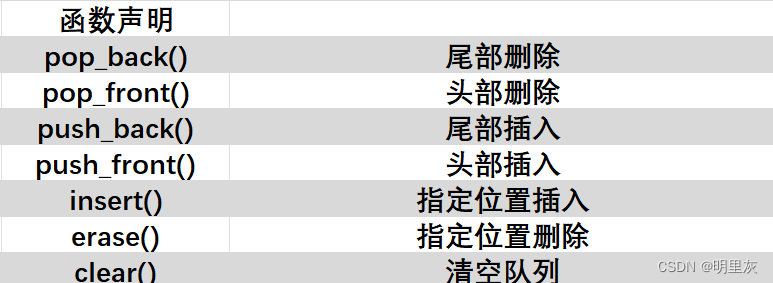
循环队列、双端队列 C和C++
队列 目录 概念 实现方式 顺序队列 循环队列 队列的数组实现 用循环链表实现队列 STL 之 queue 实现队列 STL 之 dequeue 实现双端队列 概念 队列是一种特殊的线性表,它只允许在表的前端(称为队头,front)进行删除操作…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
