棱形打印--进阶2(Java)
棱形打印
问题
* *** ***** ******* ********* ******* ***** *** * * * * *** *** *** ***** ***** ***** ******* ******* ******* *************************** ******* ******* ******* ***** ***** ***** *** *** *** * * * * * * * * *** *** *** *** *** ***** ***** ***** ***** ***** ******* ******* ******* ******* *******
**************************************************** ******* ******* ******* ******* ***** ***** ***** ***** ***** *** *** *** *** *** * * * * * * * * *** *** *** ***** ***** ***** ******* ******* ******* *************************** ******* ******* ******* ***** ***** ***** *** *** *** * * * * *** ***** ******* ********* ******* ***** *** * 分析
上图的棱形打印我们可以看成是一个大棱形的每个点有变成了一个个的小棱形,我们称整体的棱形为外套棱形,外套棱形的点变成的小棱形称为内嵌棱形。
之前我们打印过单个的棱形,类似于下面的:
* *** *****
******* -棱1***** *** *
像-棱1这种的棱形打印的方法有很多,
普通棱形打法1
像初学者可能会这样做:
先打印这一行的空格
再打印这一行的*,然后一行行的打,这是最没有技术含量的的打法。
数理思维好一点的可能会采用下面的两种打印方法
普通棱形打法2
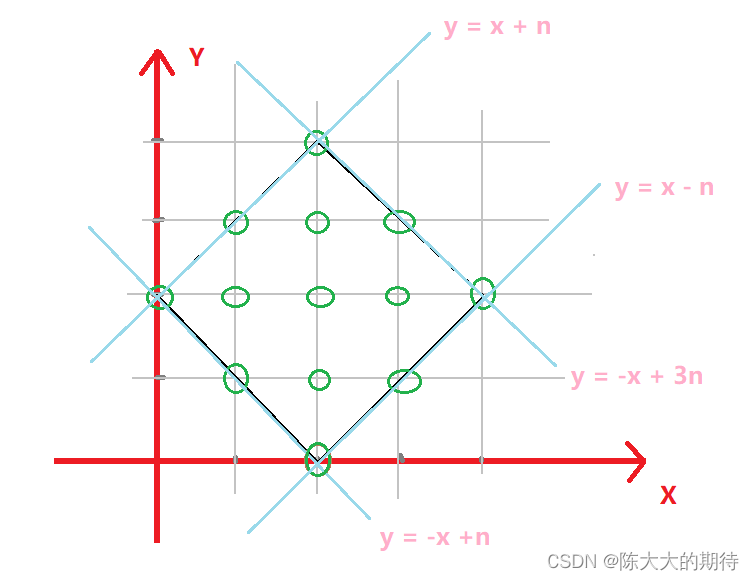
如上图 ,我们要打印一个半径为2的棱形,绿色的圆就是我们要在程序中用
*代替的,我们发现所有的圆点都在四条直线上或者在四条直线的内部所以我们得到四个判断条件,只要满足这四个条件,那么这个点在我们的程序中就是
*而不是空格
n <= x + y
x + y <= 3n
x - y >= -n
x - y <= n
所以我们写出一部分代码,用来判断这个点是否是*
public static boolean isTrue(int i ,int j ,int n){int temp = Math.abs(i-j) ;// if (( (temp) <= n ) && ( (i+j)<=(3*n) && ( n <= (i+j) )) ){ //实心棱形if (( (temp) == n ) || ( (i+j)==(3*n) || ( n == (i+j) )) ){ //空性棱形return true;}else {return false;}
}
普通棱形打法3(围点打棱)
* * *
* ==> *** *** *** * ==> ***** ***** *** ==> ******* * ***** *** *
棱心 1层 2层 3层
在 打法2 的基础上可以完成想上面的棱形打印顺序,不过打印起来需要3层for循环(不推荐),但是需要打印* * * * * * * * * * * * * * * * * * * * *
* * * * * ** * * * * * * * * * * * * * * * * * * * *
这种间隔层的棱形,就需要一层层的打。
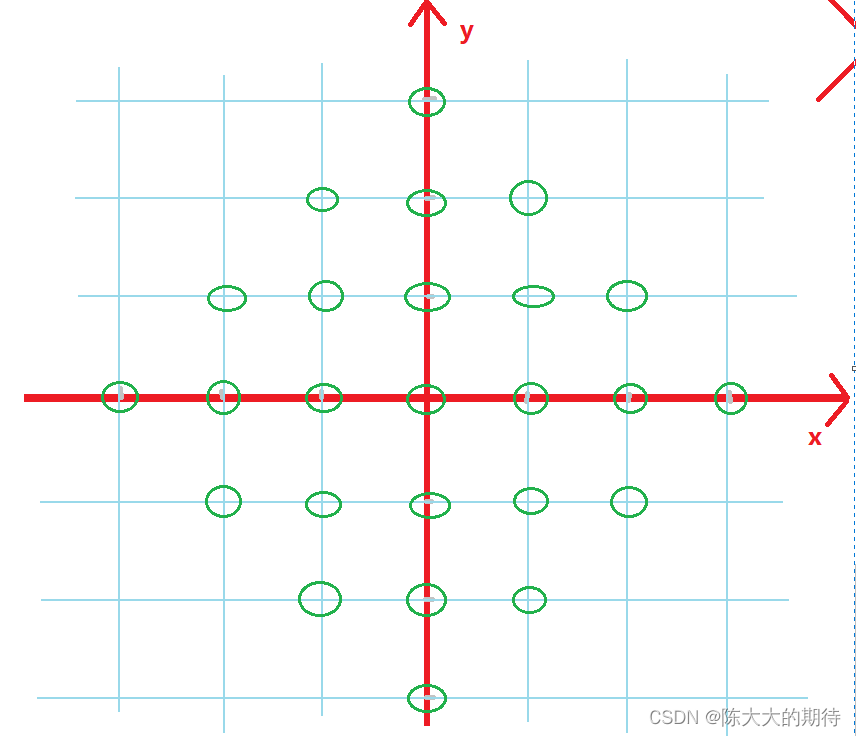
如上图(0,0)为棱心,3为半径的一个棱形,我们会发现所有棱形内的点都满足 |x| + |y| <= 3
上面是理想状态下,下面是我们实际的控制台输出坐标模式,有时候我们的棱心坐标任意呢,依然满足上面的条件
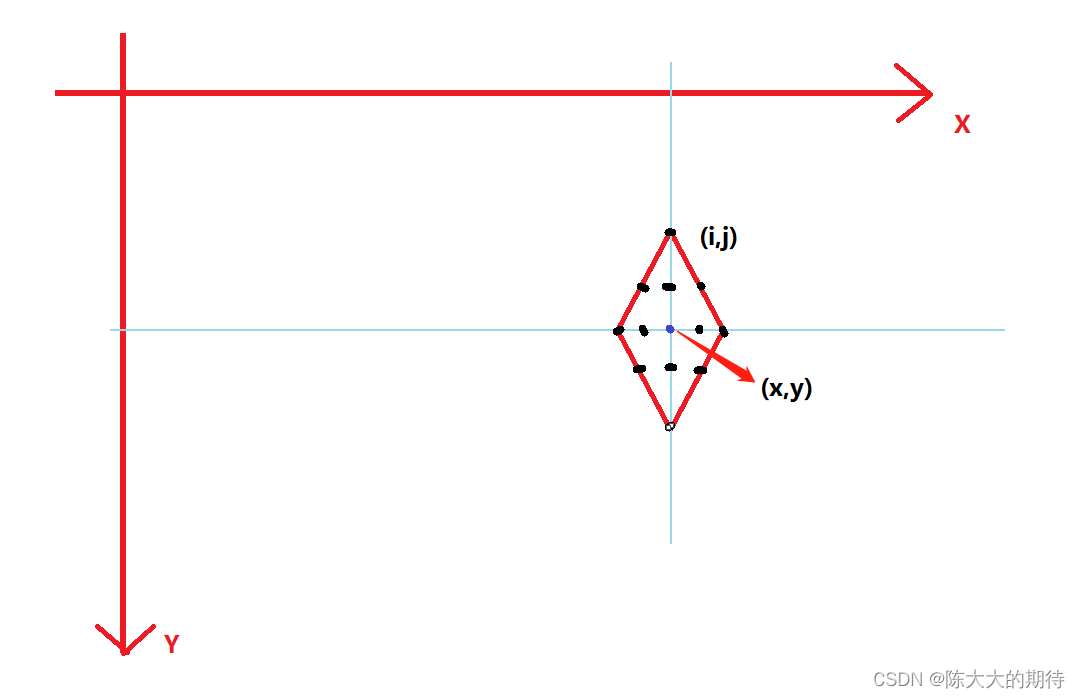
所以我们可以写出如下代码:
//判断这个点是否是我们棱形上的点
public static boolean isOne(int i ,int j ,int x ,int y , int len){if ((Math.abs(x-i) + Math.abs(y-j) <= len)){return true;}return false;
}
本题分析
看我们本题需要打印的图形,从整体上来看,是一个大棱形;再细看大棱形都是由一个个的小棱形组成的,而且看起来小棱形就是大棱形的点,在这里,我们称大棱形叫外套棱形,小棱形叫内嵌棱形。
我们获取到外套棱形的每个点,然后对每个点实行围点打棱这样就能打印出本题的图形了。
但是我们要知道小棱形的半径和大棱形的半径,当然一个小棱形对大棱形在我们这里只能当做一个单位看
我们假设小棱形半径为:min 大棱形半径为:max
步骤
###### 1. 确认打印这个棱形需要多大的纸(数组)
需要用到多大的纸取决于我们的最大值,就是棱形的对角线长度:
小棱形最多需要 minLen=(2*min+1)
大棱形最多需要 (2*max+1)
所以我们的纸最小为 (2*min+1)(2*max+1) = maxLen
int[][] array = new int[maxLen][maxLen];
2. 在数组中标记棱形的点
我们需要先找到所有小棱形的棱形,小棱形的棱形棱心与大棱形有关,如下:
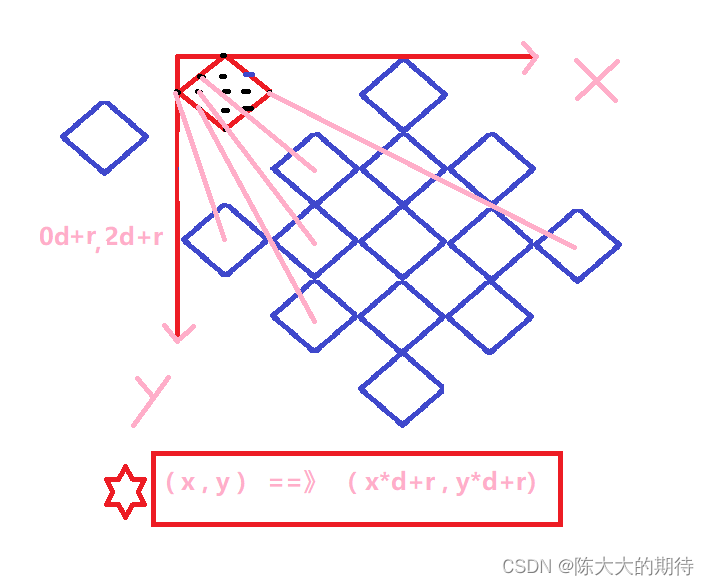
如上图:红色的棱形为外套棱形的初始状态,经过变换后,外套棱形的所有点都变为小棱形(蓝色棱形),所有的蓝色棱形组合一起就变成了我们需要的大棱形
所以我们需要先建一个简单的外套棱形,然后找到简单的外套棱形与复杂棱形之间的关系
我们发现,所有外套棱形的小棱形的棱心与简单外套棱形上的点存在以下关系
小棱形半径
minR= min小棱形直径
minD= 2*minR+1
变换关系
( x , y ) ===>>> (x*minD + minR , y*minD+minR)
得到变换关系之后 ,我们可以通过外套棱形的半径max先构建一个简单棱形,在通过变换关系将我们的纸上的所有内嵌棱形棱心标记,最后通过围点打棱打印出问题所需要的棱形
代码
/*** @Author chen_jiapin* @Date 2023/2/13 8:45* @Version 1.0* 打印棱形 column line*/
public class PrintPrismatic {public static void main(String[] args) {Scanner sc = new Scanner(System.in);System.out.println("请输入内嵌棱形的半径(int):");int min = sc.nextInt();System.out.println("请输入外套棱形的半径(int):");int max = sc.nextInt();int[][] array = initArr(min,max);int[][] maxArray = fun_02(max);int minD = 2*min+1;int minR = min;for (int i = 0; i < maxArray.length; i++) {for (int j = 0; j < maxArray[i].length; j++) {if (maxArray[i][j]==1){int maxX = i*minD+minR;int maxY = j*minD+minR;array[maxX][maxY]=1;fun_03(array,maxX,maxY,min);}}}print(array);}//初始化纸public static int[][] initArr(int min,int max){int minLen = min*2+1;int maxLen = (max*2+1)*minLen;int[][] array = new int[maxLen][maxLen];for (int i = 0; i < array.length; i++) {for (int j = 0; j < array[i].length; j++) {array[i][j] = 0 ;}}return array;}//打印简单棱形方法public static int[][] fun_02(int n){int m = 2*n+1;int[][] array = new int[m][m];for (int i = 0; i < array.length; i++) {for (int j = 0; j < array[i].length; j++) {array[i][j]=0;}}toWork(array,n);return array;}//标记纸上的点public static void fun_03(int[][] array,int x,int y,int len){array[x][y] = 1 ;for (int i = 0; i < array.length; i++) {for (int j = 0; j < array[i].length; j++) {if (isOne(i,j,x,y,len)){array[i][j]=1;}}}}//标记简单棱形上的点public static void toWork(int[][] array ,int n){array[n][n]=1;for (int i = 0; i < array.length; i++) {for (int j = 0; j < array[i].length; j++) {if (isOne(i,j,n,n,n)){array[i][j]=1;}}}}//判断点是否在棱形内public static boolean isOne(int i ,int j ,int x ,int y , int len){if ((Math.abs(x-i) + Math.abs(y-j) <= len)){return true;}return false;}//更具数组打印棱形public static void print(int[][] array){int line = 0;for (int i = 0; i < array.length; i++) {line++;int column = 0;for (int j = 0; j < array[i].length; j++) {column++;if (array[i][j]==1){System.out.print("*");}else System.out.print(" ");}System.out.println("\t" + column + " - " + line);}}}
控制台结果
请输入内嵌棱形的半径(int):
3
请输入外套棱形的半径(int):
4* 63 - 1*** 63 - 2***** 63 - 3******* 63 - 4***** 63 - 5*** 63 - 6* 63 - 7* * * 63 - 8*** *** *** 63 - 9***** ***** ***** 63 - 10********************* 63 - 11***** ***** ***** 63 - 12*** *** *** 63 - 13* * * 63 - 14* * * * * 63 - 15*** *** *** *** *** 63 - 16***** ***** ***** ***** ***** 63 - 17*********************************** 63 - 18***** ***** ***** ***** ***** 63 - 19*** *** *** *** *** 63 - 20* * * * * 63 - 21* * * * * * * 63 - 22*** *** *** *** *** *** *** 63 - 23***** ***** ***** ***** ***** ***** ***** 63 - 24************************************************* 63 - 25***** ***** ***** ***** ***** ***** ***** 63 - 26*** *** *** *** *** *** *** 63 - 27* * * * * * * 63 - 28* * * * * * * * * 63 - 29*** *** *** *** *** *** *** *** *** 63 - 30***** ***** ***** ***** ***** ***** ***** ***** ***** 63 - 31
*************************************************************** 63 - 32***** ***** ***** ***** ***** ***** ***** ***** ***** 63 - 33*** *** *** *** *** *** *** *** *** 63 - 34* * * * * * * * * 63 - 35* * * * * * * 63 - 36*** *** *** *** *** *** *** 63 - 37***** ***** ***** ***** ***** ***** ***** 63 - 38************************************************* 63 - 39***** ***** ***** ***** ***** ***** ***** 63 - 40*** *** *** *** *** *** *** 63 - 41* * * * * * * 63 - 42* * * * * 63 - 43*** *** *** *** *** 63 - 44***** ***** ***** ***** ***** 63 - 45*********************************** 63 - 46***** ***** ***** ***** ***** 63 - 47*** *** *** *** *** 63 - 48* * * * * 63 - 49* * * 63 - 50*** *** *** 63 - 51***** ***** ***** 63 - 52********************* 63 - 53***** ***** ***** 63 - 54*** *** *** 63 - 55* * * 63 - 56* 63 - 57*** 63 - 58***** 63 - 59******* 63 - 60***** 63 - 61*** 63 - 62* 63 - 63Process finished with exit code 0相关文章:

棱形打印--进阶2(Java)
棱形打印 问题 * *** ***** ******* ********* ******* ***** *** * * * …...

清除 git 所有历史提交记录,使其为新库
清除 git 所有历史提交记录,使其为新库需求方案需求 基于以前的仓库重新开发,这样可保留以前的配置等文件,但是需要删除全部的历史记录、tag、分支等。 方案 创建新的分支 使用 --orphan 选项,可创建1个干净的分支(无…...

pyTorch下载和cuda下载以及学习笔记
pytorch官方网站,cuda官方网站 CUDA下载:https://developer.nvidia.com/cuda-toolkit-archive CUDNN下载:https://developer.nvidia.com/rdp/cudnn-download pytorch下载:pytorch.org 任务管理器中只显示CUDA占用的专用内存&#…...

【学习总结】IMU预积分推导
本文仅用于记录自己学习总结。记录IMU预积分推导过程,不包含具体原理。 符号表示 RRR: 表示旋转矩阵 vvv: 表示速度 ppp: 表示位移 ExpExpExp: 指数映射,将旋转向量映射为旋转矩阵 w~\widetilde{w}w: 角速度观测值 f~\widetilde{f}f: 加速度观测值 bg…...

天猫商城自动化python脚本(仅供初学者学习使用)
作者:Eason_LYC 悲观者预言失败,十言九中。 乐观者创造奇迹,一次即可。 一个人的价值,在于他所拥有的。可以不学无术,但不能一无所有! 技术领域:WEB安全、网络攻防 关注WEB安全、网络攻防。我的…...
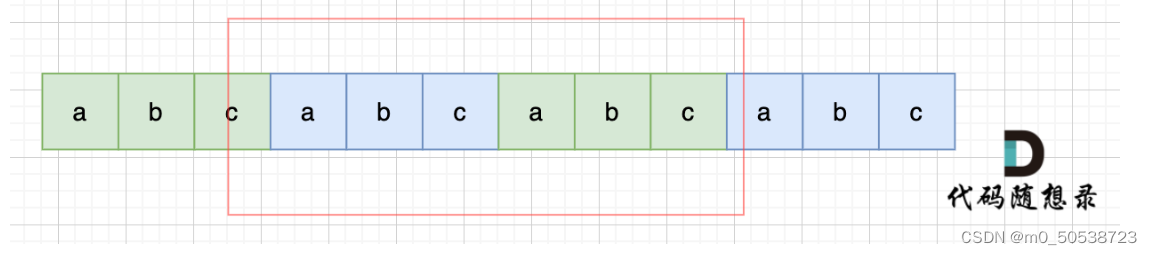
代码随想录第十一天(459)
文章目录459. 重复的子字符串答案思路暴力破解移动匹配459. 重复的子字符串 也不知道为啥这个提示简单题…… 答案思路 暴力破解 例如:abcabc 移位一次:cabcab 移位两次:bcabca 移位三次:abcabc 现在字符串和原字符串匹配了…...

线程及线程池学习
1 线程和进程的区别?进程:进程指正在运行的程序。线程:线程是进程中的一个执行单元,负责当前进程中程序的执行,一个进程中至少有一个线程。同一个进程中的多个线程之间可以并发的执行。2 创建线程有哪几种方式…...
整合Ehcache、Redis、Memcached、jetcache、j2cache缓存)
SpringBoot整合(四)整合Ehcache、Redis、Memcached、jetcache、j2cache缓存
企业级应用主要作用是信息处理,当需要读取数据时,由于受限于数据库的访问效率,导致整体系统性能偏低。 为了改善上述现象,开发者通常会在应用程序与数据库之间建立一种临时的数据存储机制,该区域中的数据在内存…...

想要的古风女生头像让你快速get
如今我看到很多人都喜欢用古风女生当作头像,那么今天我就来教大家如何快速得到一张超美的古风女生头像~ 上图就是我使用 APISpace 的 AI作画(图像生成)服务 快速生成的古风女生头像,不仅可以限定颜色,还可以选择『宝石镶嵌』或『花卉造型』这…...

传统企业数字化转型,到底难在哪里?
数字化转型过程中面临最大的挑战和问题是什么?这篇整理了企业在数字化转型过程中普遍面临的9大问题和挑战以及如何解决这些问题,希望能够对各位企业数字化转型有多启发和帮助。 01 企业数字化转型三大现状 在梳理企业数字化转型问题之前,我想…...
)
Python:青蛙跳杯子(BFS)
题目描述 X 星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。 X 星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。 如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个…...

6.10 谱分解
文章目录计算方法代码实现计算方法 单纯矩阵normal matrix指的是符号ATAAATA^TAAA^TATAAAT的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理Spectral theorem&…...

MySQL入门篇-MySQL 行转列小结
备注:测试数据库版本为MySQL 8.0 需求:求emp表各个岗位的工资之和,如无,用0代替 如需要scott用户下建表及录入数据语句,可参考:scott建表及录入数据sql脚本 CASE语法 SELECT deptno,ifnull(sum(case when job MANAGER then sal else 0 …...

项目管理常见的十大难题及其症状
01缺少维护文档时常,项目工作紧张时,第一个去掉的就是文档工作。有时即使项目有时间,也不会创建文档;或是创建了文档,却很少在项目进行过程中维护它。症状产品与需求文档不符;技术文档过时,无法保证技术的延…...

技术方案模板
0.基本原则 1.可量化,很大、很多、很高 到底是多少?基本没影响,到底有没有影响什么情况下有影响? 2.可实施,结合实际情况最终可落地 3.可指导,非方案制定人能理解,能在尽量少的人工沟通的情况下实现方案 4.可复用,设计的方案,再次出现类似需求时可以做到少开发或不…...

MySQL中对于单表和多表的操作
一、单表查询素材: 表名:worker-- 表中字段均为中文,比如 部门号 工资 职工号 参加工作 等显示所有职工的基本信息。mysql8.0 [chap03]>select * from worker;查询所有职工所属部门的部门号,不显示重复的部门号。mysql8.0 [cha…...

MFI认证
一、什么是MFI认证? 苹果MFI认证,是苹果公司(Apple Inc.)对其授权配件厂商生产的外置配件的一种使用许可,MFi认证是apple公司Made for iPhone/iPad/iPod的英文缩写。是指分别为连接iPhone/iPad/iPod而特别设计的电子配件。 [图片] 二、iOS外设连接的几种方式 [图片] 这…...

Vue中mixins的使用
文章目录mixins介绍mixins特点mixins介绍 Mixins:在引入组件之后与组件中的对象和方法进行合并,相当于扩展了父组件的对象与方法,可以理解为形成了一个新的组件。混入 (mixins):是一种分发 Vue 组件中可复用功能的非常灵活的方式…...
【PyQt】PyQt学习(一)框架介绍+环境搭建
简介 写在最前面的话 在决定学习、使用一个框架之前需要考量如下几点: 框架运行效果;框架应用范围;框架学习成本和迁移成本;实现自己所需功能的开发效率; 只有综合考量如上四个方面,才能更好地选择适合…...

浅谈前端设计模式:策略模式和状态模式的异同点
一、策略模式 策略模式是定义一系列的算法,把它们一个个封装起来, 并且使它们可相互替换。 而且策略模式是重构小能力,特别适合拆分“胖逻辑”。 这个定义乍一看会有点懵,不过通过下面的例子就能慢慢理解它的意思。 先来看一个真实场景 某次活动要做…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
