代码随想录算法训练营第四十三天 | 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
打卡第43天,01背包应用。
今日任务
- 1049.最后一块石头的重量 II
- 494.目标和
- 474.一和零
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
代码随想录
题目求石头 最小的可能重量 ,就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
求全部石头的一半重量的最大价值(这里的价值跟重量一样),本意是分成两堆大小尽可能的石头,所以递推公式:dp[j]=max(dp[j],dp[j−stones[i]]+stones[i]);dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);dp[j]=max(dp[j],dp[j−stones[i]]+stones[i]); 当前这个石头取或不取 求最大价值。
二维数组dp
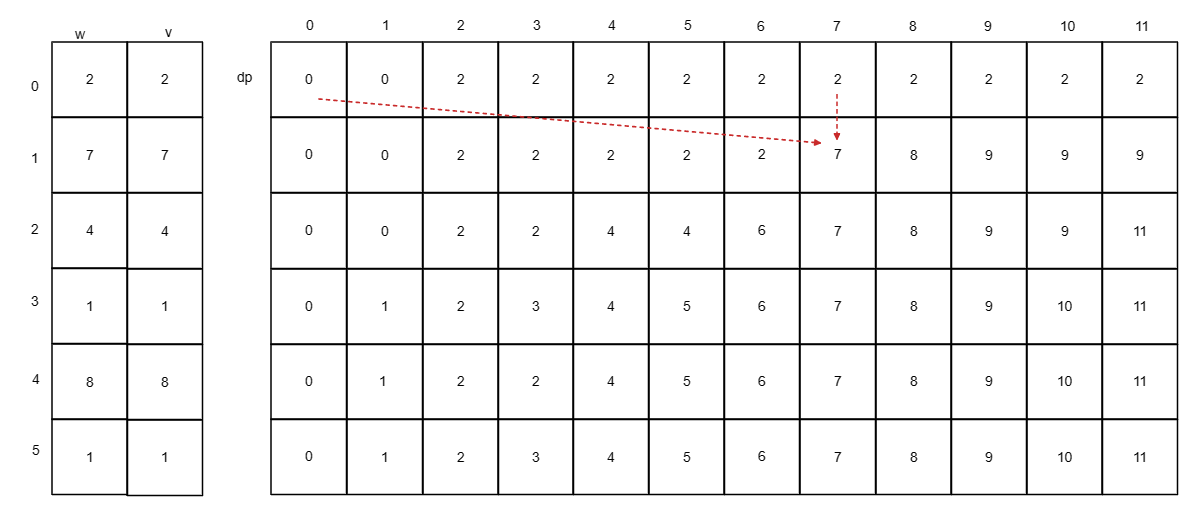
利用滚动数组:递推公式 dp[j]=max(dp[j],dp[j−stones[i]]+stones[i]);dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);dp[j]=max(dp[j],dp[j−stones[i]]+stones[i]);
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int stone : stones) sum += stone;int target = sum / 2;vector<int> dp(target + 1, 0);for(int i = stones[0]; i <= target; i++) dp[i] = stones[0]; //初始化for(int i = 1; i < stones.size(); i++) {for(int j = target; j >= stones[i]; j--) {dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]); // 递推公式}}return sum - 2 * dp[target];}
};
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
我的题解
用回溯做了一下

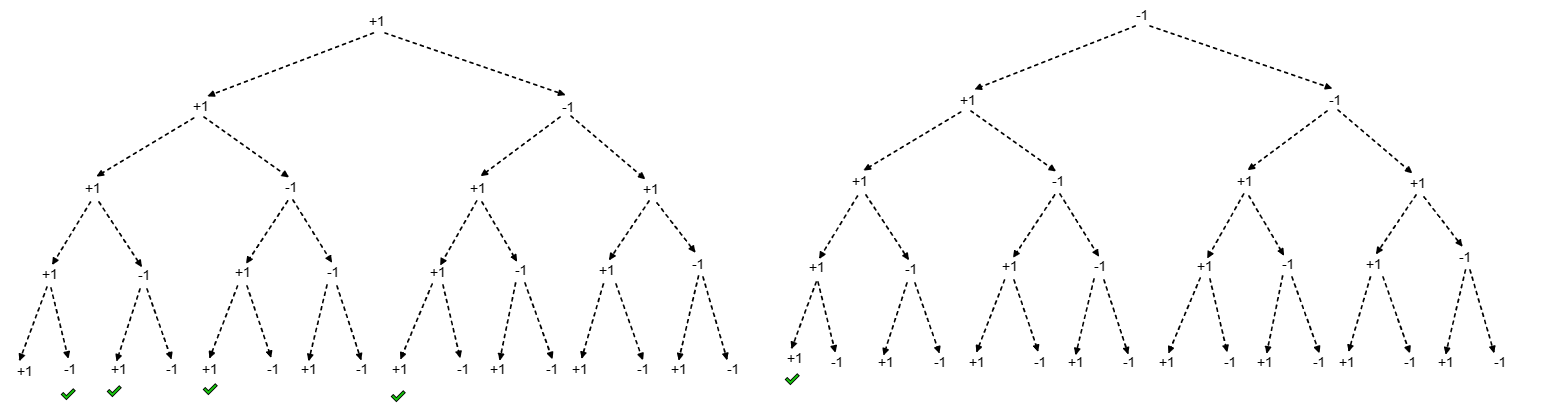
class Solution {
public:int cnt = 0;void backtracking(vector<int>& nums, int size, int target) {if(size >= nums.size()) {if(target == 0) cnt++;return ;}target -= nums[size];size++;backtracking(nums, size, target);size--;target += nums[size];target += nums[size];size++;backtracking(nums, size, target);size--;target -= nums[size];}int findTargetSumWays(vector<int>& nums, int target) {backtracking(nums, 0, target);return cnt;}
};
代码随想录
动态规划:(目标值 + 和)/ 2 = 公式全部正数dpNum,用这个公式求出正数,然后动态规划,找出是否有整数和等于dpNum。
- 确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法。 - 递推公式
只要搞到nums[i]),凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
dp[j]+=dp[j−nums[i]dp[j] += dp[j - nums[i]dp[j]+=dp[j−nums[i]
3. 初始化
dp[0] = 1; dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
4. 确定遍历顺序
nums放在外循环,target在内循环,且内循环倒序。
5. 举例推导dp数组
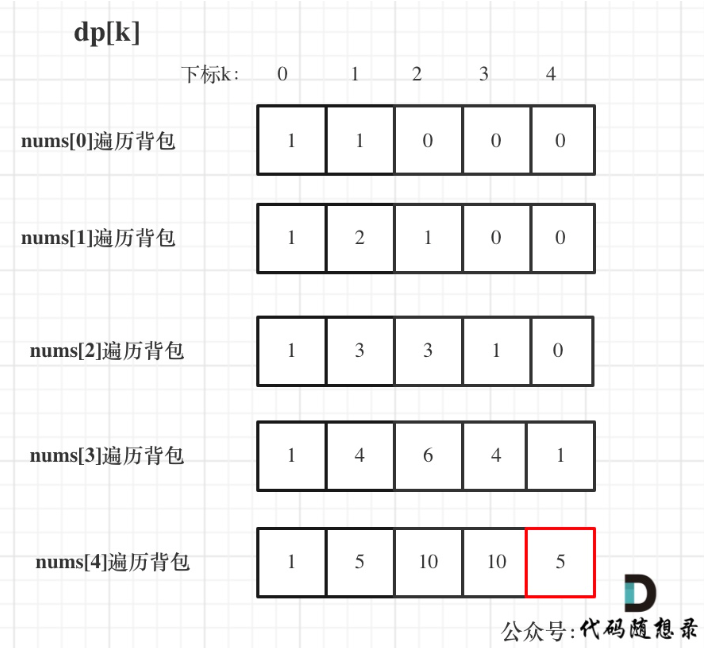
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {// 分两半 一半正数,一半负数 正数 + 负数 = 目标值 和 = 正数 - 负数 目标值 + 和 = 2 * 正数int sum = 0;for(int num : nums) sum += num;if((sum + target) % 2 == 1 || abs(target) > sum) return 0;int dpNum = (sum + target) / 2;vector<int> dp(dpNum + 1, 0);dp[0] = 1;for(int i = 0; i < nums.size(); i++) {for(int j = dpNum; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];// printf("%d ", dp[j]);}// printf("\n");}return dp[dpNum];}
};
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
代码随想录
-
确定dp数组以及下标的定义
dp[i][j]:最多有i个0和j个1的str的最大子集的大小dp[i][j]。 -
递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
-
初始化
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。 -
遍历顺序
for循环遍历物品,内层for循环遍历背包容量且从后向前遍历! -
举例
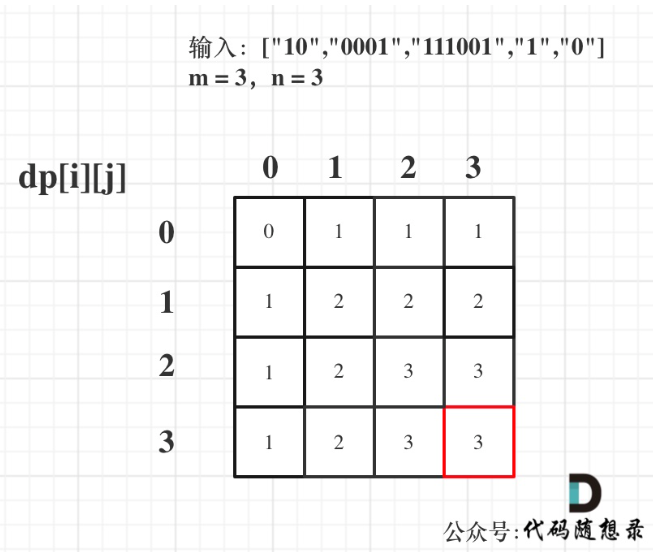
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0for (string str : strs) { // 遍历物品int oneNum = 0, zeroNum = 0;for (char c : str) {if (c == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};
相关文章:

代码随想录算法训练营第四十三天 | 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
打卡第43天,01背包应用。 今日任务 1049.最后一块石头的重量 II494.目标和474.一和零 1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头࿰…...

PostCSS 让js可以处理css
GitHub 中文readmie PostCSS 中文网(建设中) PostCSS 不是样式预处理器 是 CSS 语法转换的工具,但不严格遵循css规范,只要符合css语法规则就可以被处理。这也让提前实现新提案成为可能。 使用 webpack 中使用 postcss-loader …...

【C语言进阶:自定义类型详解】位段
本节重点内容: 什么是位段位段的内存分配位段的跨平台问题位段的应用⚡什么是位段 位段的声明和结构是非常类似的,但是有两个不同: 位段的成员必须是 int、unsigned int 或signed int 。位段的成员名后边有一个冒号和一个数字。 struct A…...
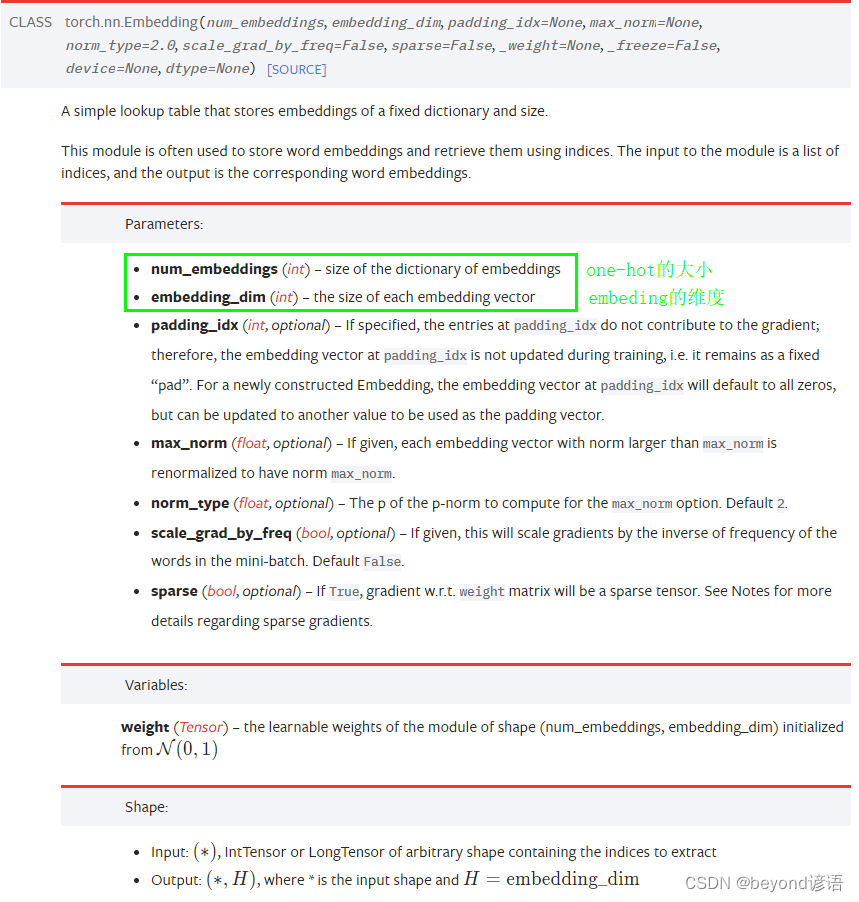
十三、RNN循环神经网络实战
因为我本人主要课题方向是处理图像的,RNN是基本的序列处理模型,主要应用于自然语言处理,故这里就简单的学习一下,了解为主 一、问题引入 已知以前的天气数据信息,进行预测当天(4-9)是否下雨 日期温度气压是否下雨4-…...
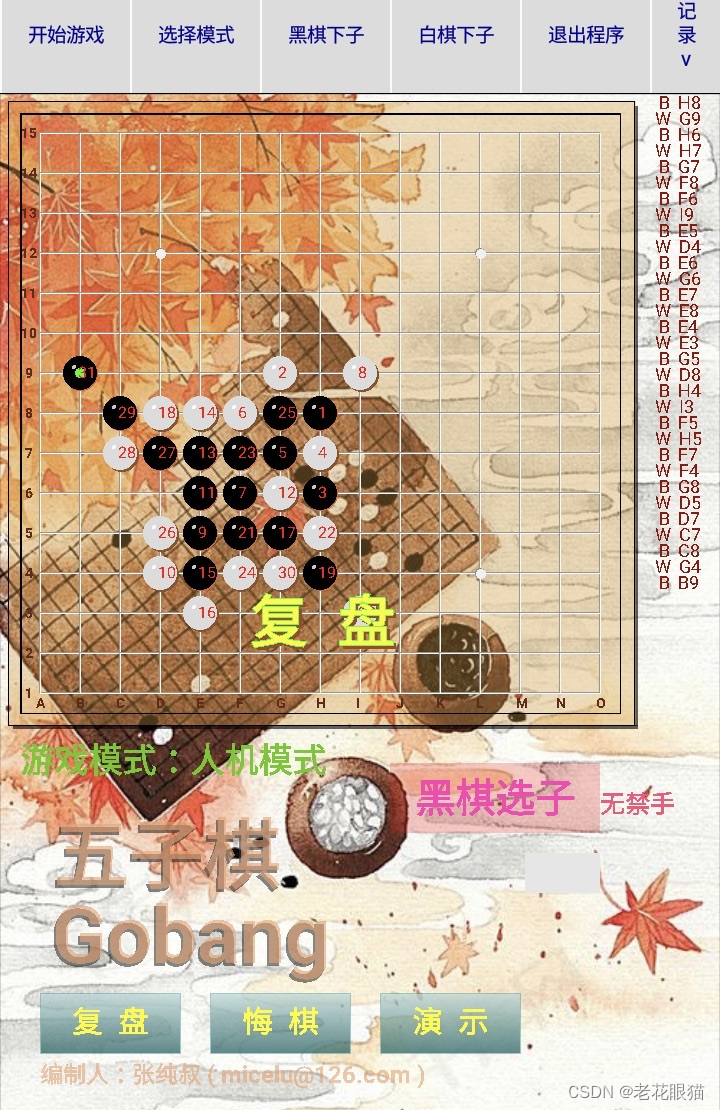
五子棋透明棋盘界面设计(C语言)
五子棋透明棋盘设计,漂亮的界面制作。程序设置双人对奕,人机模式,对战演示三种模式。设置悔棋,记录功能,有禁手设置。另有复盘功能设置。 本文主要介绍透明的玻璃板那样的五子棋棋盘的制作。作为界面设计,…...
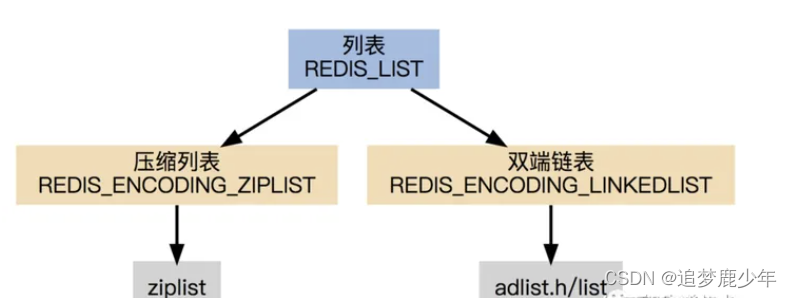
Redis第六讲 Redis之List底层数据结构实现
List数据结构 List是一个有序(按加入的时序排序)的数据结构,Redis采用quicklist(双端链表) 和 ziplist 作为List的底层实现。可以通过设置每个ziplist的最大容量,quicklist的数据压缩范围,提升数据存取效率 list-max-ziplist-size -2 // 单个ziplist节点最大能存储 8kb ,…...
真题,含答案解析)
电子学会2023年3月青少年软件编程python等级考试试卷(四级)真题,含答案解析
目录 一、单选题(共25题,共50分) 二、判断题(共10题,共20分) 三、编程题(共3题,共30分)...

【MATLAB】一篇文章带你了解beatxbx工具箱使用
目录 一篇文章带你了解beatxbx工具箱使用 一篇文章带你了解beatxbx工具箱使用 clc;clear; tic; % step1 初始化 % 个体数量 NIND = 35; % 最大遗传代数 MAXGEN = 180; % 变量的维数 NVAR = 2; % 变量的二进制位数 % 上下界 bounds=[-10 10-10 10]; precision=0.0001; %运算精度…...

【LinuxC Sqlite数据库小项目】基于Sqlite的打卡系统------适合初学者练手的小项目
最近小哥老是想浪,不想好好学习,这不行啊,得想点办法,多少做点努力,于是就自己给自己写了个打卡程序; 该程序基于Sqlite数据库,实现一个简单的打卡功能,该函数具有自动初始化的功能…...

在掌握C#基础上再学习C语言
C#和C语言虽然名字相似,但它们在很多方面都有很大的区别。 首先,C#是一种面向对象的语言,而C语言是过程化的语言。这意味着C#具有更丰富的语言特性,如类、接口、继承和多态性等,而C语言则更侧重于直接对计算机硬件进行…...

HTML5 <body> 标签
HTML <body> 标签 实例 一个简单的 HTML 文档,包含尽可能少的必需的标签: <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>文档标题</title> </head><body> 文档内容…...

(链表)反转链表
文章目录前言:问题描述:解题思路:代码实现:总结:前言: 此篇是针对链表的经典练习。 问题描述: 给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1…...
deb文件如何安装到iphone方法分享
Cydia或同类APT管理软件在线安装 Cydia或同类APT管理软件在线安装,这个是最佳的安装方式,因为通常无需考虑依赖关系,但缺点是对网络的要求比较高;命令行中以dpkg-iXXX.deb的形式安装,好处是可以以通配符一次性安装多个deb,而且也可以直接看到脚本的运行状况和安装成功/失…...
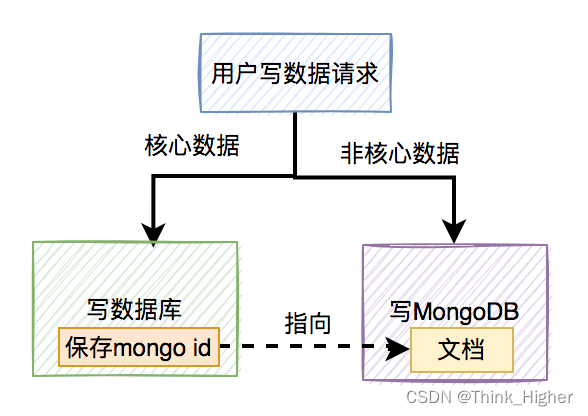
mongodb和mysql双写数据一致性问题
文章目录 我们是如何用MongoDB的如何保证双写一致性?先写数据库,再写MongoDB先写MongoDB,再写数据库用户修改操作如何保存数据如何清理新增的垃圾数据定时删除随机删除我们是如何用MongoDB的 MongoDB是一个高可用、分布式的文档数据库,用于大容量数据存储。文档存储一般用…...

Databend 开源周报第 88 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.com 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 Support Eager…...
Vue3学习笔记(9.4)
Vue3自定义指令 除了默认设置的核心指令(v-model和v-show),Vue也允许注册自定义指令。 下面我们注册一个全局指令v-focus,该指令的功能是在页面加载时,元素获得焦点: <!--* Author: RealRoad10834252…...
 错误)
导入 Excel 文件时,抛出 413 (Request Entity Too Large) 错误
Excel文件大小:8MB 异常信息:413 (Request Entity Too Large) 环境:IIS10PHP7.2.33 依次检查如下几项: 一、php.ini Maximum amount of memory a script may consume (128MB) 限制代码消耗的最大内存,默认128…...

Verilog学习笔记1——关键词、运算符、数据类型、function/task、initial/always、generate
文章目录前言一、关键词二、运算符三、数据类型1、基本类型:reg、wire、integer、parameter四、条件语句五、循环语句1、for2、generate六、function和task七、initial和always1、initial和always相同点和区别2、always和assign语句区别前言 2023.4.4 2023.4.7 补充…...
)
探索LeetCode【0005】最长回文子串(未搞懂,未练习)
目录0、题目1、第一个官方答案1.1 动态规划(未懂)1.2 中心扩展(已懂)1.3 Manacher(未懂)2、第二个参考答案2.1 暴力求法(已懂)2.2 反转法(未懂)2.3 动态规划&…...

使用 Docker run 命令简化容器化
使用 Docker run 命令简化容器化 Docker run 是在 Docker 容器中运行应用程序的基本命令。在开始使用 Docker 之前,了解一些重要的命令非常重要。 在本博客中,我们将解释 Docker run 命令的基本语法,并探索其一些最常见的选项,以…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
