代码随想录算法训练营第五十一天 | 309. 最佳买卖股票时机含冷冻期、714. 买卖股票的最佳时机含手续费
309. 最佳买卖股票时机含冷冻期
动规五部曲
1、确定dp数组以及下标的含义
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
具体可以区分出如下四个状态:
- 状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
- 不持有股票状态,这里就有两种卖出股票状态
- 状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
- 状态三:今天卖出股票
- 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
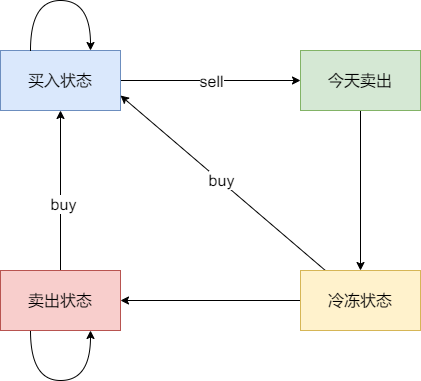
j的状态为:
- 0:状态一
- 1:状态二
- 2:状态三
- 3:状态四
注意这里的每一个状态,例如状态一,是持有股票股票状态并不是说今天一定就买入股票,而是说保持买入股票的状态即:可能是前几天买入的,之后一直没操作,所以保持买入股票的状态。
2、确定递推公式
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作:
- 操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
- 操作二:今天买入了,有两种情况
- 前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态(状态二),dp[i - 1][1] - prices[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作:
- 操作一:前一天就是状态二
- 操作二:前一天是冷冻期(状态四)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作:
昨天一定是持有股票状态(状态一),今天卖出
即:dp[i][2] = dp[i - 1][0] + prices[i];
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作:
昨天卖出了股票(状态三)
dp[i][3] = dp[i - 1][2];
3、dp数组如何初始化
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],一定是当天买入股票。
保持卖出股票状态(状态二),只能初始为0
今天卖出了股票(状态三),同上分析,dp[0][2]初始化为0,dp[0][3]也初始为0。
4、确定遍历顺序
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历。
5、举例推导dp数组
以 [1,2,3,0,2] 为例,dp数组如下:
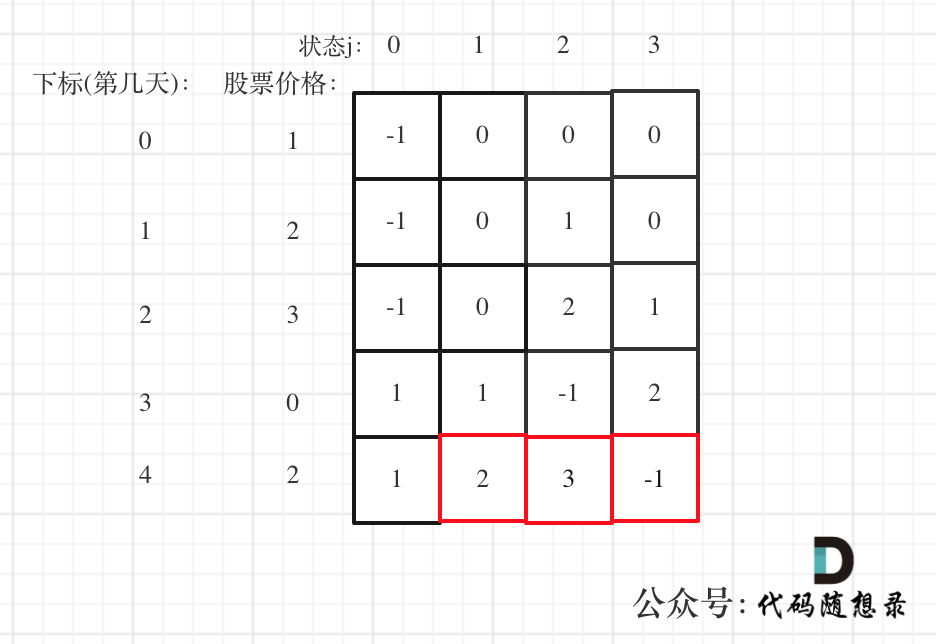
最后结果是取 状态二,状态三,和状态四的最大值
状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;int len = prices.size();vector<vector<int>> dp(len, vector<int>(4,0));dp[0][0] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i],dp[i - 1][1] - prices[i]));dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2];}return max(dp[len - 1][1], max(dp[len - 1][2], dp[len - 1][3]));}
};714. 买卖股票的最佳时机含手续费
与普通买卖股票问题一致,手续费可以放在买入股票时,也可以放在卖出股票时进行计算
本题把手续费算入买入股票时
动规五部曲:
1、确定dp数组以及下标的含义
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
可以分为两种状态:状态一:不持有股票(j为0);状态二:持有股票(j为1)
2、确定递推公式
不持有股票状态:有两种情况
- 昨天不持有
- 昨天持有,今天把昨天股票卖出
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]
持有股票状态:
- 昨天已持有
- 昨天未持有,今天买入股票
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
3、dp数组如何初始化
不持有股票 dp[0][0] = 0;
持有股票 dp[0][1] = -prices[0] - fee;
4、确定遍历顺序
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历。
5、举例推导dp数组
以 prices = [1, 3, 2, 8, 4, 9], fee = 2 为例

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2,0));dp[0][0] = 0;dp[0][1] = -prices[0] - fee;for (int i = 1; i < prices.size(); i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);}return max(dp[prices.size() - 1][0], dp[prices.size() - 1][1]);}
};相关文章:

代码随想录算法训练营第五十一天 | 309. 最佳买卖股票时机含冷冻期、714. 买卖股票的最佳时机含手续费
309. 最佳买卖股票时机含冷冻期 动规五部曲 1、确定dp数组以及下标的含义 dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。 具体可以区分出如下四个状态: 状态一:持有股票状态(今天买入股票,或者是…...

中英文拼写检测纠正开源项目使用入门 word-checker 1.1.0
项目简介 word-checker 本项目用于单词拼写检查。支持英文单词拼写检测,和中文拼写检测。 特性说明 可以迅速判断当前单词是否拼写错误 可以返回最佳匹配结果 可以返回纠正匹配列表,支持指定返回列表的大小 错误提示支持 i18n 支持大小写、全角半角…...

面试如果还不会Netty,看这篇文章就够了
我们去面试的时候,经常被问到netty的题目。我整理了netty的32连问。小伙伴们,收藏起来慢慢看吧。 1. Netty是什么,它的主要特点是什么? Netty是一个高性能、异步事件驱动的网络编程框架,它基于NIO技术实现࿰…...
作为大学生,你还不会搭建chatGPT微应用吗?
目录 引言ChatGPT是什么?背景:ChatGPT敢为人先,打破全球僵局示例演示:基于ChatGPT微应用实现的条件及步骤(1)整体框架(2)搭建前的准备工作(3)实际搭建步骤&a…...

Three.js教程:第一个3D场景
推荐:将NSDT场景编辑器加入你3D工具链其他工具系列:NSDT简石数字孪生下面的代码完整展示了通过three.js引擎创建的一个三维场景,在场景中绘制并渲染了一个立方体的效果,为了大家更好的宏观了解three.js引擎, 尽量使用了…...

lua快速入门~在js基础上,知道Lua 和 Js 的不同即可
☺ lua 和 javaScript 差不多的,就是一些语法的细节不同,学过js,再注意一下下面的细节,就能上手了~ 快速入门,可以直接看一下菜鸟教程的lua:https://www.runoob.com/lua/lua-tutorial.html Lua 和 Js 的不同…...

Linux系统【Centos7】更换源详细教程
更换CentOS 7系统的源可以提高网络速度,加快软件升级和安装的速度。以下是详细的更换CentOS 7源实践。 步骤 1:备份原始 Yum.repo 在更换之前,首先要备份原始 Yum.repo 文件(一定要记得备份)。 bash sudo mv /etc/y…...

金三银四求职季来了!分享几道最常见的app面试题,帮助您更好准备面试求职!
目录:导读 引言 一、Web 端测试和 App 端测试有何不同? 二、App是如何测试的? 三、app闪退的可能原因? 四、给你一个登录页面,你要如何测试? 五、测试过程中遇到app出现crash或者ANR,你会怎么处理? …...
Java集合——List接口学习总结
一、ArrayList实现类 1. 常用方法 增加:add(int index, E element)删除:remove(int index) remove(Object o)修改:set(int index, E element)查看:get(int index)判断:常用遍历方式://List集合 遍历&…...
低代码平台前端技术组件选型1.0(前端))
低代码(三)低代码平台前端技术组件选型1.0(前端)
目前国内主流的低代码开发平台有:金蝶、用友、宜搭、云程、简道云、明道云、氚云、伙伴云、道一云、JEPaaS、华炎魔方、搭搭云、JeecgBoot 、RuoYi等。这些平台各有优劣势,定位也不同,用户可以根据自己需求选择。如果企业想自主可控ÿ…...

代码随想录算法训练营第35天|860.柠檬水找零,406.根据身高重建队列,452. 用最少数量的箭引爆气球
代码随想录算法训练营第35天|860.柠檬水找零,406.根据身高重建队列,452. 用最少数量的箭引爆气球860.柠檬水找零406. 根据身高重建队列452. 用最少数量的箭引爆气球860.柠檬水找零 题目链接:860.柠檬水找零,难度:简单…...

C++整人代码,十分朴实但威力无穷,让你对cout怀疑人生,整死你的同学
cout人人皆知 /a 只是让电脑响个铃 直接上个简单的代码 #include<iostream> using namespace std; int main() {while(1)cout<<"\a"; }最后普及一下: 控制符的作用有: setbase(n) 以n进制方式输出(n8,10,16) setfill(ch) 设置…...
【Spring Cloud Alibaba】12.定时任务(xxl-job)
文章目录简介什么是xxl-job调度中心执行器官方架构图相关地址环境要求配置调度中心下载源码目录说明初始化数据库源码方式docker方式测试集群(可选)配置执行器pom.xmlapplication.propertiesXxlJobExecutorApplication.java执行器组件配置创建定时任务任…...
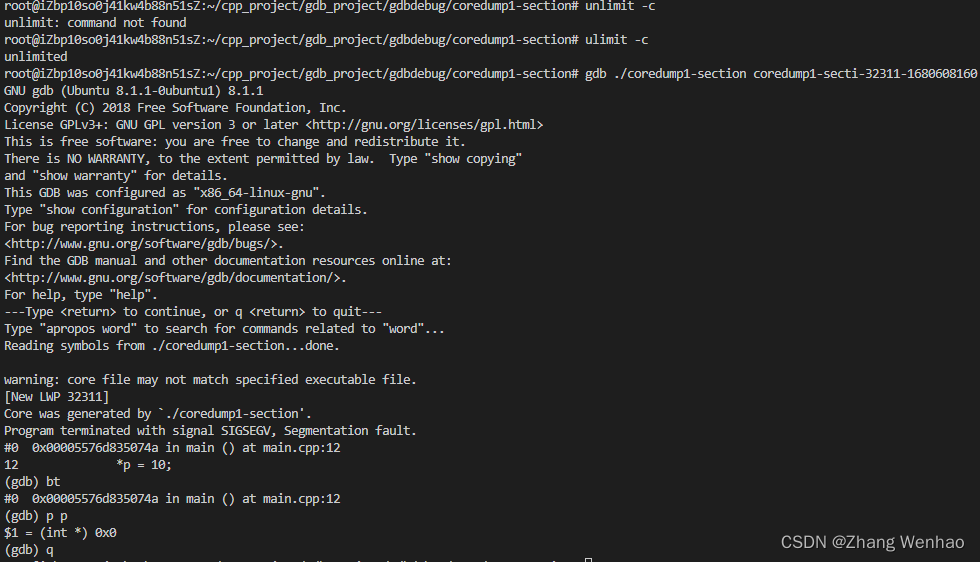
GDB core dump分析
基本知识 Linux core dump:一般称之为核心转储、内核转储,我们统称为转储文件。是某个时刻某个进程的内存信息映射,即包含了生成转储文件时该进程的整个内存信息以及寄存器等信息。转储文件可以是某个进程的,也可以是整个系统的。…...
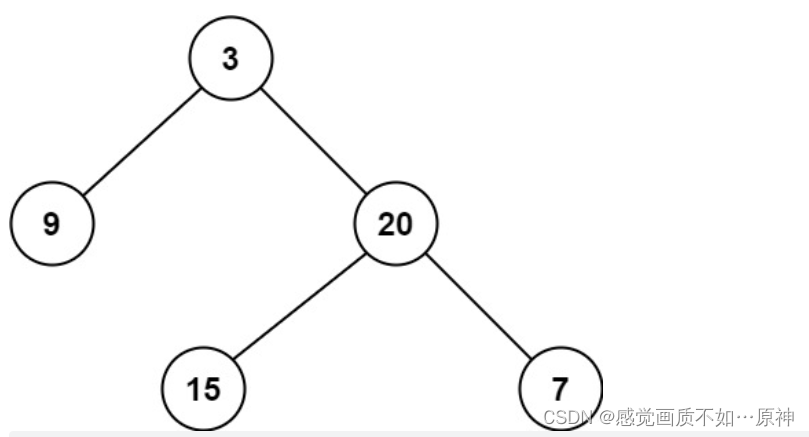
Leetcode.111 二叉树的最小深度
题目链接 Leetcode.111 二叉树的最小深度 easy 题目描述 给定一个二叉树,找出其最小深度。 最小深度是从 根节点 到 最近叶子节点 的 最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例 1: 输入:root [3,9,20,null,nul…...

【RP-RV1126】SDK编译常用记录
文章目录一、单独编译1.1 单独配置编译kernel1.2 单独编译配置Buildroot1.3 单独编译rkmedia1.3.1 添加自己的rkmedia代码文件荣品的RV1126。一、单独编译 如果执行 build.sh 运行完成后没有在 rockdev/ 目录下生成镜像文件,请执行: ./build.sh firmwa…...
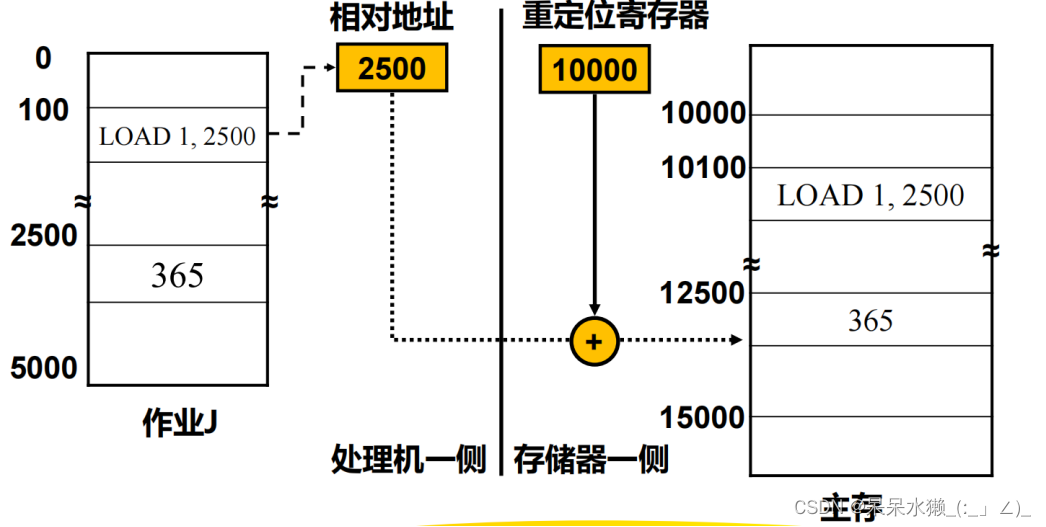
【操作系统复习】第5章 存储器管理
存储器的层次结构 存储层次 ➢ CPU寄存器 ➢ 主存:高速缓存、主存储器、磁盘缓存 ➢ 辅存:固定磁盘、可移动介质 层次越高,访问速度越快,价格也越高,存储容量也最小 寄存器和主存掉电后存储的信息不再存在&a…...
Python人工智能在气象中的实践技术应用
专题一 Python 和科学计算基础 1.1 Python 入门和安装 1.1.1 Python 背景及其在气象中的应用 1.1.2 Anaconda 解释和安装以及 Jupyter 配置1.1.3 Python 基础语法 1.2 科学数据处理基础库 1.2.1 Numpy 库1.2.2 Pandas 库1.2.3 Scipy 库 1.2.4 Matplotlib 和 Cartopy 库 …...
libcurl库的安装及使用说明
目录 一 libcurl库安装 ① 下载网址 ② libcurl库安装步骤 ③ libcurl等第三方库的通用编译方法 二 调用libcurl编程访问百度主页 ① 代码说明 ② 编译说明 ③ 执行说明 三 libcurl的使用说明 ① curl相关函数简介 ② curl_easy_setopt函数部分选项介绍 ③…...
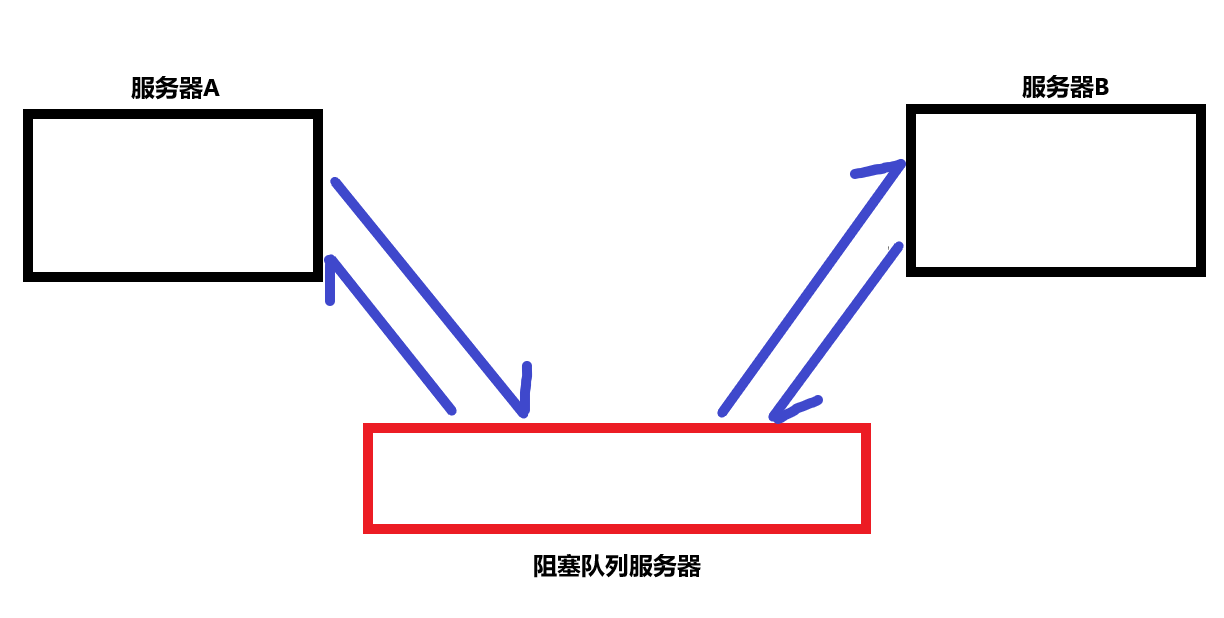
【JAVAEE】手把手教学多线程,包教包会~
线程与进程为了实现多个任务并发执行的效果,人们引进了进程。何谓进程?我们电脑上跑起来的每个程序都是进程。每一个进程启动,系统会为其分配内存空间以及在文件描述符表上有所记录等。进程是操作系统进行资源分配的最小单位,这意…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
