微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间内部(interior)(而不是端点处)的条件。
法国数学家米歇尔·罗尔 (Michel Rolle) 于 1691 年首次发表了以他的名字命名的定理。然而,在此之前,罗尔是微积分最直言不讳的批评者之一,指出微积分给出的结果是错误的,而且是基于不可靠的推理。在晚年,罗尔开始看到微积分的用处。
罗尔定理(Rolle’s Theorem):令f在闭区间[a,b]上连续,在开区间(a,b)上可导。假如f (a) = f (b),则在开区间(a,b)中存在至少一个点c,满足f ’(c) = 0。
或者,换一种描述。令f为满足以下三个假设条件(hypotheses)的函数:
(1) f在闭区间[a,b]上连续,
(2) f在开区间(a,b)上可导,
(3) f (a) = f (b),
则在开区间(a,b)中存在至少一个点c,满足f ’(c) = 0。
对于这几个假设条件的理解:
(1) 假设f 在闭区间[a,b]上连续,这一条实际是满足极值定理的条件,满足这个条件,就说明函数f在闭区间[a,b]上既有最大值也有最小值,只不过这个极值有可能发生在两个端点处。
(2) 假设f 在开区间(a,b)上可导,也就是说函数f在开区间上的导数存在。为什么要刨去两个端点呢?因为在这两个端点处,导数可能不存在;另外,定理是为了将极值限定在开区间内部。函数在开区间内可导,就排除了3种情况:任何不连续点,点不连续,自然没法产生变化率;角点(corners),即函数产生了突变,没有一个明确定义的导数,角点处左右极限不相等;垂直切线,垂直切线没有导数,且函数值没有最大最小,无穷大无穷小。
(3) f (a) = f (b),这个条件是为了把常量函数包括进去,常量函数其导数为0;此外,限定了两点的函数相等,从直观上来说,不管你函数图像在闭区间中是上升还是下降,你的函数值最终都会回到这个值,既然上升了,又下降到这个值,那么你中间一定有一个极大值,反之亦然;例如,函数在a点之后上升了,那么由于这个条件的限制,你在某一处一定会下降,从而回到b点时下降到等于a点的函数值;对于a点之后下降了也是一样的道理。
参考资料:
<<calculus>> Ron Larson,The Pennsylvania State University The Behrend College
Bruce Edwards, University of Florida
<<calculus>> James Stewart
相关文章:
)
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…...
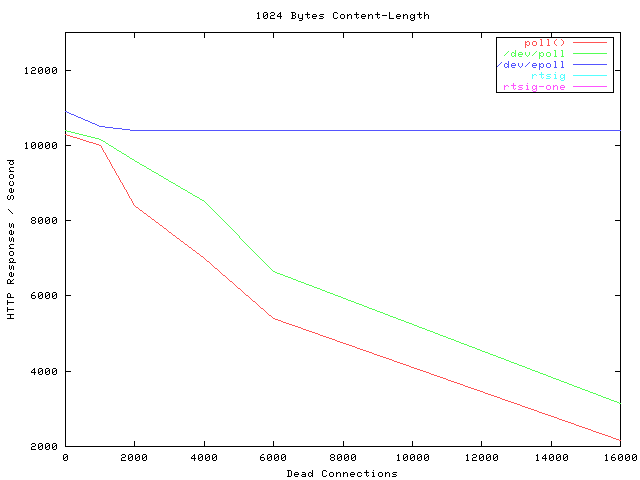
linux内核之select/poll/epoll
一些主流应用IO多路复用技术,突破高并发问题,如nginx、redis、netty,分布式服务框架dubbo,大数据组件hadoop、spark、flink、hbase纷纷使用netty作为网络通信组件。 一、背景:C10K问题 The C10K problem 最早被Dan …...

文件流下载
文件下载 后端传给前端json数据流,前端拿到之后存放在自定义的文件中import axios from "axios"; import qs from "query-string"; import {Notification } from "@arco-design/web-vue"; // 接口中需要含有文件名fileName export function dow…...

C语言模拟实现:atoi函数
在实现atoi之前我们先来了解一下atoi函数的作用是什么: 目录 1.实例演示 2.模拟实现 2.1 判断是否为空指针 2.2判断是否为空字符串 2.3判断正负号 2.4判断非数字字符 2.5判断是否越界 2.6完整代码 1.实例演示 //实例演示 #include <stdio.h> #include …...
LeetCode.每日一题 2427. 公因子的数目
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
蓝牙BQB认证 - HFP profile配置说明
零.声明 本专栏文章我们会以连载的方式持续更新,本专栏计划更新内容如下: 第一篇:蓝牙综合介绍 ,主要介绍蓝牙的一些概念,产生背景,发展轨迹,市面蓝牙介绍,以及蓝牙开发板介绍。 第二篇:Trans…...
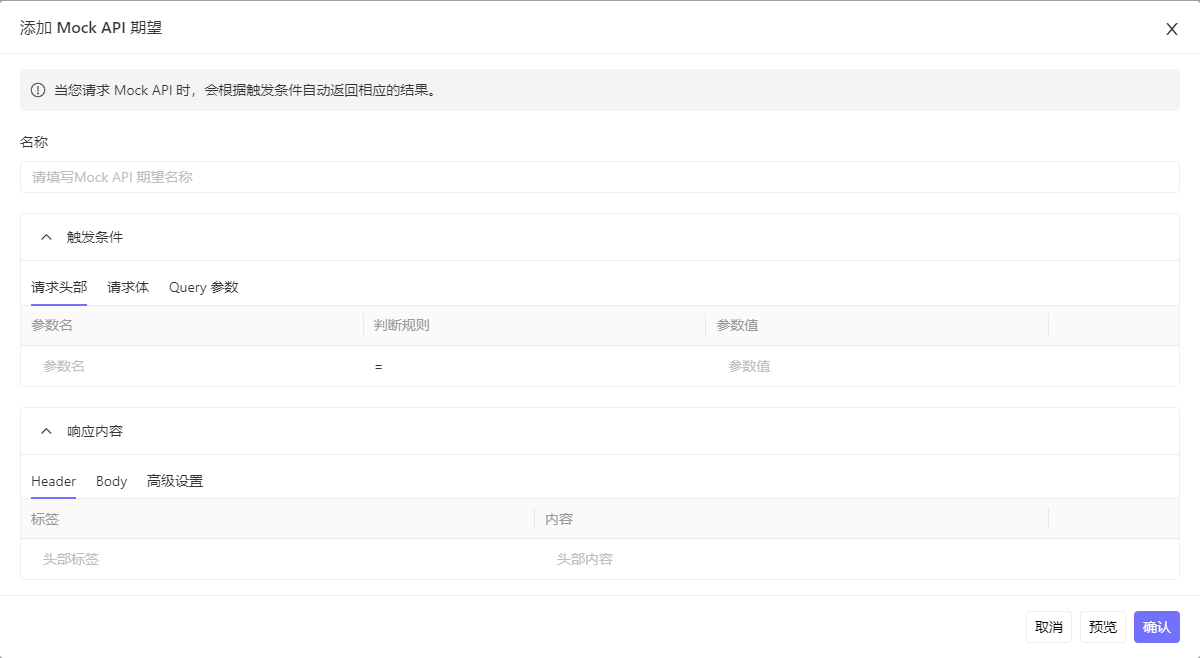
【接口测试工具】Eolink Apikit 快速入门教程
Eolink Apikit 下载安装【官方版】:https://www.eolink.com/apikit 发起 API 测试 进入 API 文档详情页,点击上方 测试 标签,进入 API 测试页,系统会根据 API 文档自动生成测试界面并且填充测试数据。 填写请求参数 首先填写好请…...

使用Python和OpenCV实现实时人脸检测并保存截图
在本篇博客中,我们将使用Python和OpenCV库实现一个实时人脸检测的小项目。我们将利用OpenCV中的Haar级联分类器来检测摄像头捕获的图像中的人脸。 项目功能 通过摄像头实时捕获视频流。使用Haar级联分类器检测视频帧中的人脸。在检测到的人脸周围绘制矩形框。实时…...

[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过
文章目录背景前情回顾描述方法约定MEMCG总览省流总结简介slub 相关 memcg机制kernel 5.9 版本之前结构体初始化具体实现kernel 5.9-5.14kernel 5.14 之后突破slab限制方法cross cache attackpage 堆风水总结背景 前情回顾 关于slab几个结构体的关系和初始化和内存分配和释放的…...
)
MySQL创建数据库(CREATE DATABASE语句)
在 MySQL 中,可以使用 CREATE DATABASE 语句创建数据库,语法格式如下: CREATE DATABASE [IF NOT EXISTS] <数据库名> [[DEFAULT] CHARACTER SET <字符集名>] [[DEFAULT] COLLATE <校对规则名>]; [ ]中的内容是可选的。语…...

【JavaWeb】4—Tomcat
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 如果文章对你有所帮助,可以点赞👍…...
宝塔Linux面板部署Python flask项目
目录 👉1、前言 👉2、安装python项目管理器 👉3、上传项目文件及文件夹 👉4、配置项目 👉5、请求测试 学习记录: 👉1、前言 写在前面:前几天我们实现了外网内外登录正方教务系…...

spring中产生bean的几种方式
BeanImportMyImportSelector implements ImportSelectorMyImportBeanDefinitionRegistarimplements ImportBeanDefinitionRegistrarFactoryBean这里着重讲解FactoryBean如何判断当前bean是否是FactoryBeanorg.springframework.beans.factory.support.AbstractBeanFactory#isFac…...

OD-火星文计算(Python)
火星文计算 题目描述 已经火星人使用的运算符号为# $ 其与地球人的等价公式如下x#y2*x3*y4x$y3*xy2x y是无符号整数 地球人公式按照c语言规则进行计算 火星人公式中$符优先级高于#相同的运算符按从左到右的顺序运算 输入描述 火星人字符串表达式结尾不带回车换行 输入的字符…...

【vue3教程】初入了解vue3的基本结构
前言 Animatrix:黑客帝国 Blade Runner:银翼杀手 Cowboy Bebop:星际牛仔 Dragon Ball:龙珠 Evangelion:新世纪福音战士 Ghostin the Shell:攻壳机动队 Hunter X Hunter:全职猎人 Initial D&…...

智慧供水综合运营平台解决方案
一、概述 建设背景: 供水系统是城市生存、发展的基础,供水事业的发展与城市的社会经济发展息息相关,其服务质量的好坏不仅关系到供水企业自身的利益,也直接影响到社会的稳定和政府形象。住房城乡建设部于2012年12月5日正式发布了《…...
文件系统、描述符和缓冲区
目录 🏆一、文件系统 1、open ①对open接口的介绍 ②接口使用 2、write接口 3、read接口 🏆二、深入理解文件描述符fd 1、fd具体实质 2、文件fd的分配规则 3、fd重定向 ①输出重定向 ②追加重定向 ③输入重定向 ④文件的引用计数 🏆三…...
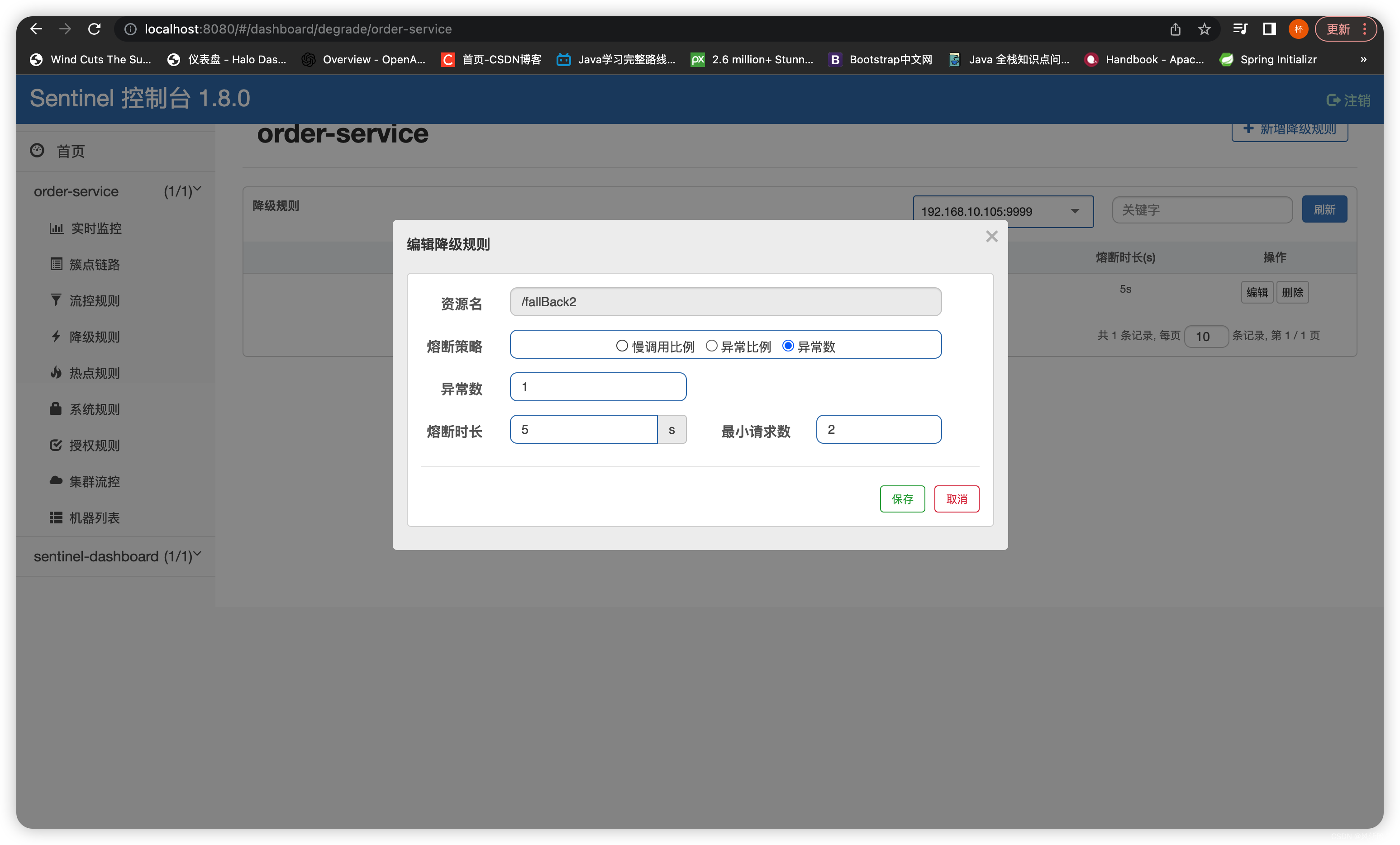
java微服务商城高并发秒杀项目--009.流控规则和降级规则
线程流控(只要线程数达到了指定数量,访问就会被流控):warm up流控效果(慢慢增加QPS的数量,之后最后达到阈值,这种情况下,一开始会容易限流,后期就不会限流了)…...

php编写的脚本,如何才能在windows系统运行呢?
咱们要在Windows系统上运行PHP脚本,需要安装PHP解释器和Web服务器。 以下是基本的步骤,很简单: 下载PHP解释器:可以从官方网站 https://windows.php.net/download/ 下载Windows版本的PHP解释器。根据你的操作系统和需要的版本选…...
政务综合服务平台建设项目方案书
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除 目 录 第一章 项目整体概述 1.1. 项目名称 1.2. 建设单位 1.3. 编写依据 1.3.1 相关政策 1.3.2 技术标准 1.4. 建设目标、规模、内容、建设期 1.4.1 建设目标 1.4.2 …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
