python 实现二叉搜索树的方法有哪些?
树的介绍
树不同于链表或哈希表,是一种非线性数据结构,树分为二叉树、二叉搜索树、B树、B+树、红黑树等等。
树是一种数据结构,它是由n个有限节点组成的一个具有层次关系的集合。用图片来表示的话,可以看到它很像一棵倒挂着的树。因此我们将这类数据结构统称为树,树根在上面,树叶在下面。一般的树具有以下特点:
- 每个节点有0个或者多个子节点
- 没有父节点的节点被称为根节点
- 每个非根节点有且只有一个父节点
- 每个子结点都可以分为多个不相交的子树
二叉树的定义是:每个节点最多有两个子节点。即每个节点只能有以下四种情况:
- 左子树和右子树均为空
- 只存在左子树
- 只存在右子树
- 左子树和右子树均存在
二叉搜索树
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

列举几种Python中几种常见的实现方式:
1.使用类和递归函数实现
通过定义一个节点类,包含节点值、左右子节点等属性,然后通过递归函数实现插入、查找、删除等操作。代码示例如下:
class Node:def __init__(self, data):self.data = dataself.left = Noneself.right = None
class BST:def __init__(self):self.root = None
def insert(self, value):if self.root is None:self.root = Node(value)else:self._insert(value, self.root)
def _insert(self, value, node):if value < node.data:if node.left is None:node.left = Node(value)else:self._insert(value, node.left)elif value > node.data:if node.right is None:node.right = Node(value)else:self._insert(value, node.right)
def search(self, value):if self.root is None:return Falseelse:return self._search(value, self.root)
def _search(self, value, node):if node is None:return Falseelif node.data == value:return Trueelif value < node.data:return self._search(value, node.left)else:return self._search(value, node.right)
def delete(self, value):if self.root is None:return Falseelse:self.root = self._delete(value, self.root)
def _delete(self, value, node):if node is None:return nodeelif value < node.data:node.left = self._delete(value, node.left)elif value > node.data:node.right = self._delete(value, node.right)else:if node.left is None and node.right is None:del nodereturn Noneelif node.left is None:temp = node.rightdel nodereturn tempelif node.right is None:temp = node.leftdel nodereturn tempelse:temp = self._find_min(node.right)node.data = temp.datanode.right = self._delete(temp.data, node.right)return node
def _find_min(self, node):while node.left is not None:node = node.leftreturn node2.使用列表实现
通过使用一个列表来存储二叉搜索树的元素,然后通过列表中元素的位置关系来实现插入、查找、删除等操作。代码示例如下:
class BST:def __init__(self):self.values = []
def insert(self, value):if len(self.values) == 0:self.values.append(value)else:self._insert(value, 0)
def _insert(self, value, index):if value < self.values[index]:left_child_index = 2 * index + 1if left_child_index >= len(self.values):self.values.extend([None] * (left_child_index - len(self.values) + 1))if self.values[left_child_index] is None:self.values[left_child_index] = valueelse:self._insert(value, left_child_index)else:right_child_index = 2 * index + 2if right_child_index >= len(self.values):self.values.extend([None] * (right_child_index - len(self.values) + 1))if self.values[right_child_index] is None:self.values[right_child_index] = valueelse:self._insert(value, right_child_index)
def search(self, value):if value in self.values:return Trueelse:return False
def delete(self, value):if value not in self.values:return Falseelse:index = self.values.index(value)self._delete(index)return True
def _delete(self, index):left_child_index = 2 * index + 1right_child_index = 2 * index + 2if left_child_index < len(self.values) and self.values[left_child_index] is not None:self._delete(left_child_index)if right_child_index < len(self.values) and self.values[right_child_index] is not None:self3.使用字典实现
其中字典的键表示节点值,字典的值是一个包含左右子节点的字典。代码示例如下:
def insert(tree, value):if not tree:return {value: {}}elif value < list(tree.keys())[0]:tree[list(tree.keys())[0]] = insert(tree[list(tree.keys())[0]], value)else:tree[list(tree.keys())[0]][value] = {}return tree
def search(tree, value):if not tree:return Falseelif list(tree.keys())[0] == value:return Trueelif value < list(tree.keys())[0]:return search(tree[list(tree.keys())[0]], value)else:return search(tree[list(tree.keys())[0]].get(value), value)
def delete(tree, value):if not search(tree, value):return Falseelse:if list(tree.keys())[0] == value:if not tree[list(tree.keys())[0]]:del tree[list(tree.keys())[0]]elif len(tree[list(tree.keys())[0]]) == 1:tree[list(tree.keys())[0]] = list(tree[list(tree.keys())[0]].values())[0]else:min_key = min(list(tree[list(tree.keys())[0]+1].keys()))tree[min_key] = tree[list(tree.keys())[0]+1][min_key]tree[min_key][list(tree.keys())[0]] = tree[list(tree.keys())[0]]del tree[list(tree.keys())[0]]elif value < list(tree.keys())[0]:tree[list(tree.keys())[0]] = delete(tree[list(tree.keys())[0]], value)else:tree[list(tree.keys())[0]][value] = delete(tree[list(tree.keys())[0]].get(value), value)return tree由于字典是无序的,因此该实现方式可能会导致二叉搜索树不平衡,影响插入、查找和删除操作的效率。
4.使用堆栈实现
使用堆栈(Stack)可以实现一种简单的二叉搜索树,可以通过迭代方式实现插入、查找、删除等操作。具体实现过程如下:
- 定义一个节点类,包含节点值、左右子节点等属性。
- 定义一个堆栈,初始时将根节点入栈。
- 当栈不为空时,取出栈顶元素,并对其进行操作:如果要插入的值小于当前节点值,则将要插入的值作为左子节点插入,并将左子节点入栈;如果要插入的值大于当前节点值,则将要插入的值作为右子节点插入,并将右子节点入栈;如果要查找或删除的值等于当前节点值,则返回或删除该节点。
- 操作完成后,继续从堆栈中取出下一个节点进行操作,直到堆栈为空。
需要注意的是,在这种实现方式中,由于使用了堆栈来存储遍历树的过程,因此可能会导致内存占用较高。另外,由于堆栈的特性,这种实现方式只能支持深度优先遍历(Depth-First Search,DFS),不能支持广度优先遍历(Breadth-First Search,BFS)。
以下是伪代码示例:
class Node:def __init__(self, data):self.data = dataself.left = Noneself.right = None
def insert(root, value):if not root:return Node(value)stack = [root]while stack:node = stack.pop()if value < node.data:if node.left is None:node.left = Node(value)breakelse:stack.append(node.left)elif value > node.data:if node.right is None:node.right = Node(value)breakelse:stack.append(node.right)
def search(root, value):stack = [root]while stack:node = stack.pop()if node.data == value:return Trueelif value < node.data and node.left:stack.append(node.left)elif value > node.data and node.right:stack.append(node.right)return False
def delete(root, value):if root is None:return Noneif value < root.data:root.left = delete(root.left, value)elif value > root.data:root.right = delete(root.right, value)else:if root.left is None:temp = root.rightdel rootreturn tempelif root.right is None:temp = root.leftdel rootreturn tempelse:temp = root.rightwhile temp.left is not None:temp = temp.leftroot.data = temp.dataroot.right = delete(root.right, temp.data)return root以上是四种在Python中实现二叉搜索树的方法,在具体使用过程中还是需要合理选择,尽量以运行速度快、内存占用少为出发点,最后觉得有帮助的话请多多关注和赞同!!!
相关文章:

python 实现二叉搜索树的方法有哪些?
树的介绍 树不同于链表或哈希表,是一种非线性数据结构,树分为二叉树、二叉搜索树、B树、B树、红黑树等等。 树是一种数据结构,它是由n个有限节点组成的一个具有层次关系的集合。用图片来表示的话,可以看到它很像一棵倒挂着的树。…...

ORM概述
1_ORM概述[理解] 解释: 对象关系映射模型特点: 1.将类名,属性, 映射成数据库的表名和字段2.类的对象,会映射成为数据库表中的一行一行的数据 优缺点: 优点: 1.不再需要编写sql语句2.不再关心使用的是什么数据库了 缺点: 1.由于不是直接通过sql操作数据库,所以有性能损失 2_…...
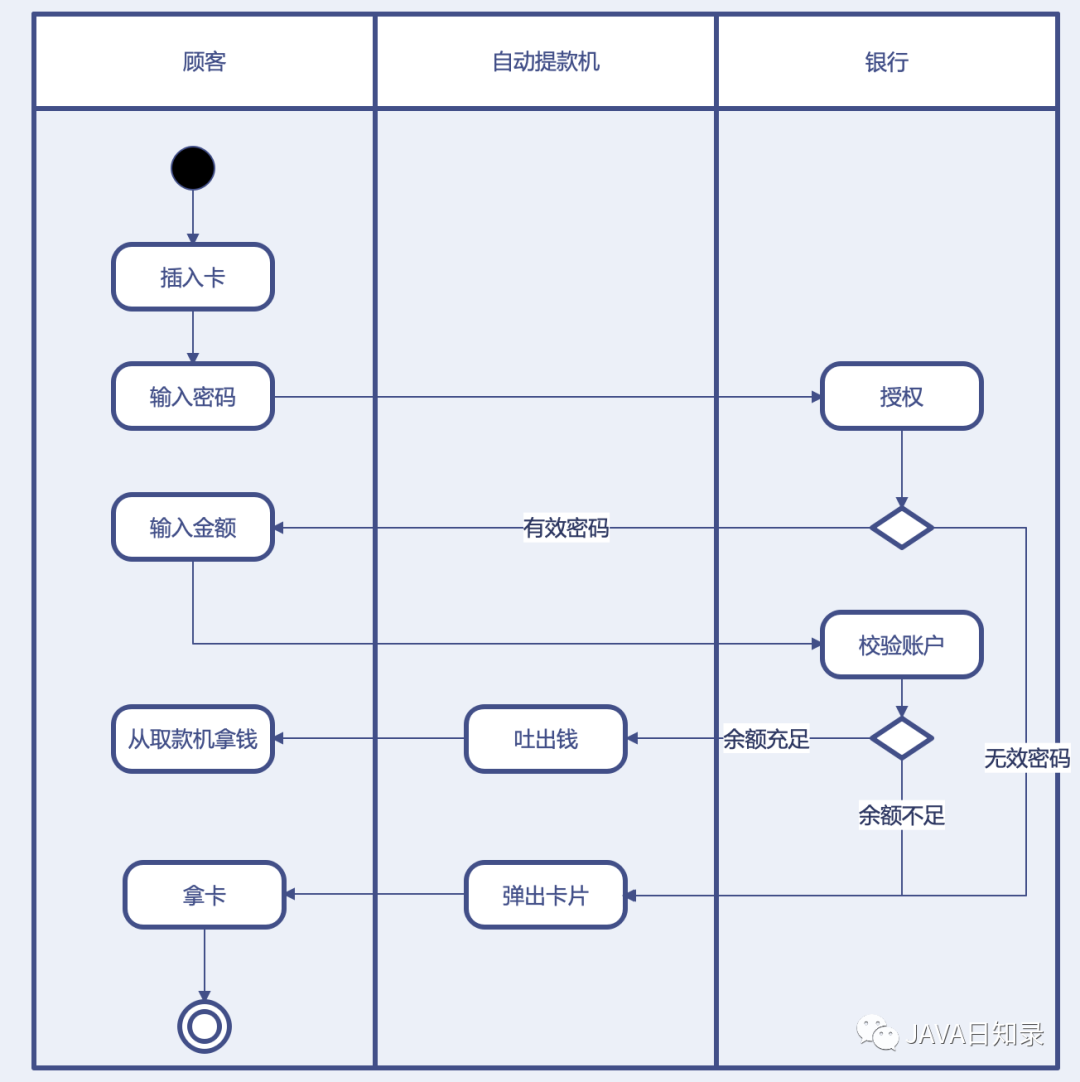
程序员必知必会7种UML图(类图、序列图、组件图、部署图、用例图、状态图和活动图)画法盘点
众所周知,软件开发是一个分阶段进行的过程。不同的开发阶段需要使用不同的模型图来描述业务场景和设计思路,在不同的阶段输出不同的设计文档也是必不可少的,例如,在需求分析阶段需要输出领域模型和业务模型,在架构阶段…...
基于asp的搜索引擎开发和实现
随着因特网的迅猛发展、WEB信息的增加,用户要在信息海洋里查找信息,就像大海捞针一样,搜索引擎技术恰好解决了这一难题。目前,搜索引擎系统可以分类三大类,分别是:目录式搜索引擎:以人工方式或半…...

代码随想录刷题-字符串-实现 strStr()
文章目录实现 strStr()习题暴力解法kmp 解法实现 strStr() 本节对应代码随想录中:代码随想录,讲解视频:帮你把KMP算法学个通透!(理论篇)_哔哩哔哩_bilibili、帮你把KMP算法学个通透!࿰…...

前端已死?金三银四?你收到offer了吗?
目录 一、前言 二、“唱衰” 三、不局限于框架、前端 四、打动面试官 五、正向加成 六、小结 一、前言 最近在脉脉、知乎等平台都有人在渲染前端从业人员的危机,甚至使用“前端已死”的字眼,颇有“语不惊人死不休”的意味,对老鸟来说&a…...

C生万物 | 十分钟带你学会位段相关知识
结构体相关知识可以先看看这篇文章 —— 链接 一、什么是位段 位段的声明和结构是类似的,有两个不同: 位段的成员必须是 int、unsigned int 或signed int位段的成员名后边有一个冒号和一个数字 在下面,我分别写了一个结构体和一个位段&…...
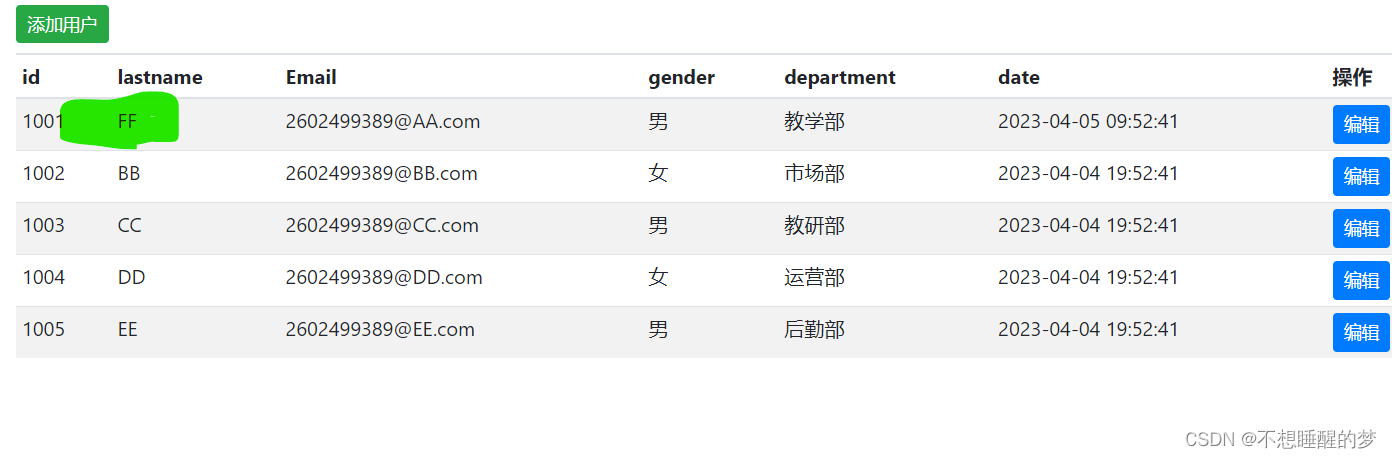
Spring Boot基础学习之(十):修改员工的信息
注意:spring boot专栏是一个新手项目,博文顺序则是功能实现的流程,如果有看不懂的内容可以到前面系列去了解。 本次项目所有能够使用的静态资源可以免费进行下载 静态资源 在本篇代码DAO层将通过Java文件去实现,在这里就不连接数…...

闭关十几天,我完成了我的毕业设计
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,也会涉及到服务端(Node.js) 📃个人状态: 在校大学生一枚,已拿多个前端 offer(…...

认识rust的项目管理工具--cargo
cargo 提供了一系列的工具,从项目的建立、构建到测试、运行直至部署,为 Rust 项目的管理提供尽可能完整的手段。不过,我们无需再手动安装,之前安装 Rust 的时候(用rustup或者vscode加插件的方式安装)&#…...
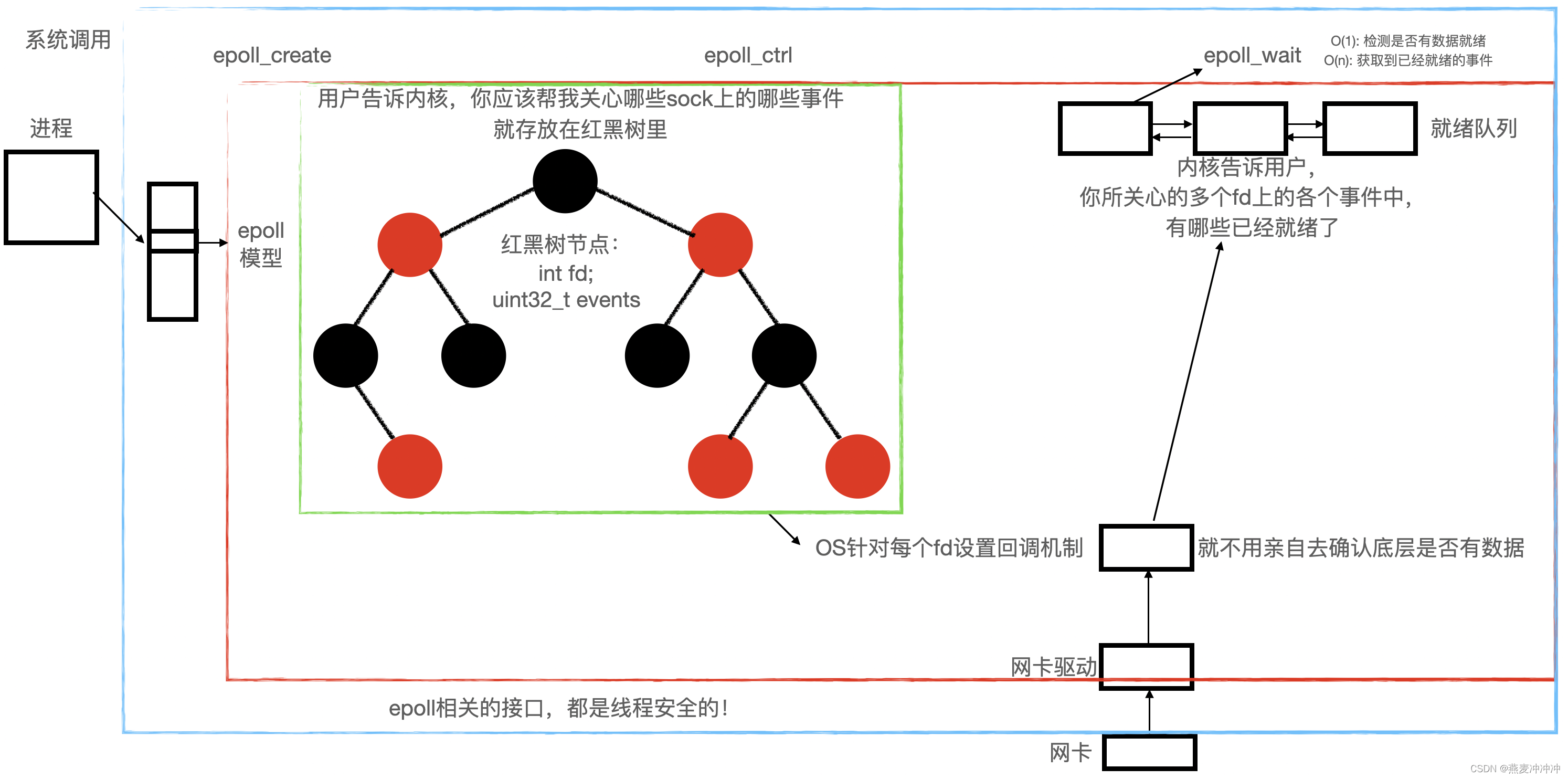
面试常问的Linux之 I/O 复用
I/O 复用 一、I/O的概念 在Linux系统中,I/O(输入/输出)指的是计算机系统的数据交换过程,包括从外部设备读取数据(输入)和将数据发送到外部设备(输出)。I/O操作是Linux系统中非常重要…...

MySQL-binlog+dump备份还原
目录 🍁binlog日志恢复 🍂binlog介绍 🍂Binlog的用途 🍂开启binary log功能 🍂配置binlog 🍁mysqldump 🍂数据库的导出 🍂数据库的导入 🍁mysqldumpbinlog 🦐…...

互联网络-单级互联网络
1.立方体单级网络 1.定义 立方体单级网络(cube)的名称来源于下图所示的三维立方体结构,如010只能连接到000、011、110,不能直接连接到对角线上的001、100、101、111。 2.例题 1.编号为0、1、2、3、4,…,15的16个处理器,用单级互联网络互联,用Cube0互联函数时,与第10…...
上海亚商投顾:沪指四连阳重回3300点 中字头个股再发力
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪大小指数今日走势分化,沪指低开后震荡反弹,创业板指盘中跌超1%。中字头个股再度发力&#x…...

LeetCode:150. 逆波兰表达式求值—栈
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱150. 逆波兰表达式求值 题目描述:给你一个字符串数组 token…...

C/C++每日一练(20230410) 二叉树专场(4)
目录 1. 二叉搜索树迭代器 🌟🌟🌟 2. 验证二叉搜索树 🌟🌟🌟 3. 不同的二叉搜索树 II 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专…...

策化整理1
概述: 本游戏是一款恐怖类解密游戏,以反应毒品的危害和反对家庭暴力为主题 在游戏中玩家扮演被困入梦境内的主人公,寻找逃出梦境的方法 本游戏故事大背景: 主人公的父亲是一名毒贩,在母亲发现父亲开始吸毒后选择与父亲…...
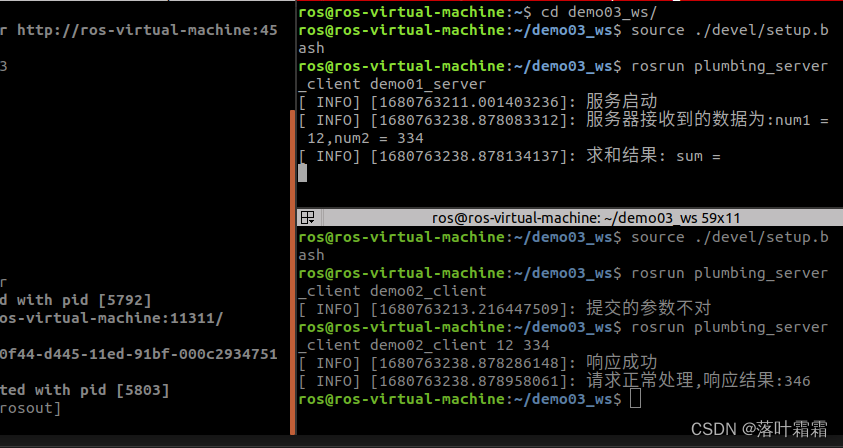
【服务通信自定义srv调用3----客户端的优化】
客户端的优化 服务通信自定义srv调用,客户端随意提交两个数,完成数的相加。也就是实现参数的动态提交: 1.格式:rosrun xxxx xxxx 12 34 2.节点执行时候,需要获取命令中的参数,并且组织进 request 代码中应…...

React跨域解决方案
一、跨域日志报错 我们由于项目需要经常会需要对不同域名、不同子域的网站接口发起请求,有时甚至是对于同一域名的不同端口发起请求,此时我们经常看到以下报错: Access to XMLHttpRequest at xxx from origin xxx has been blocked by COR…...
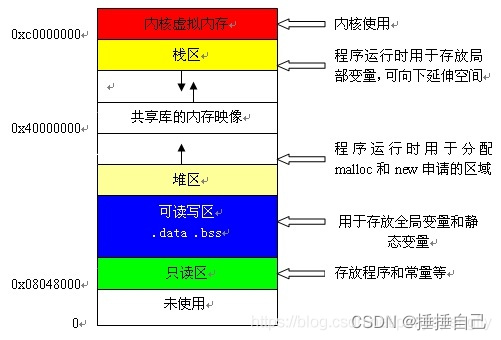
内存五区的概念,内存池技术的诞生。
首先提出一道经典的面试题来引出今天的主角: 进程的虚拟空间分布是什么样的,全局变量放在哪里? 在数据初始化之后,全局变量放在.data段 在数据未初始化时,全局变量放在.bss段 内存五区 进程虚拟内存主要分为五个部分…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
