代码随想录刷题-字符串-实现 strStr()
文章目录
- 实现 strStr()
- 习题
- 暴力解法
- kmp 解法
实现 strStr()
本节对应代码随想录中:代码随想录,讲解视频:帮你把KMP算法学个通透!(理论篇)_哔哩哔哩_bilibili、帮你把KMP算法学个通透!(求next数组代码篇)_哔哩哔哩_bilibili
习题
题目链接:28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
暴力解法
题目意思是 needle 字符串是否在 haystack 字符串中出现,如果出现返回第一次出现的位置
那么直观的解法就是遍历 haystack 字符串,不断地将当前字符串与 needle 第一个字符比较,如果相同,则再依次比较后续长度的元素是否还是等于 needle 对应位置的元素。需要注意的是遍历 haystack 字符串的边界条件是 i+needle.size()<=haystack.size(),因为一旦剩余的 haystack 字符串小于 needle 的长度,那肯定无法匹配,避免 haystack[i+j] 可能出现数组越界的情况
class Solution {
public:int strStr(string haystack, string needle) {int n = haystack.size(), m = needle.size();// 循环遍历haystack,i表示当前检查的位置for (int i = 0; i + m <= n; i++) {bool flag = true;// 循环遍历needle字符串的每个字符for (int j = 0; j < m; j++) {if (haystack[i + j] != needle[j]) { // 如果在某个字符处匹配失败,则标记flag为false,跳出循环flag = false;break; } }if (flag) { // 如果整个needle字符串都匹配上了,返回起始位置ireturn i;}}return -1;// 如果找不到needle字符串,返回-1}
};
- 时间复杂度:O(m∗nm*nm∗n)。通过两层循环实现字符串匹配,外层循环的次数是 n - m + 1(其中n是haystack的长度,m是needle的长度),内层循环的次数是needle的长度m。因此,该算法的时间复杂度为 O(nm)
- 空间复杂度:O(111)。用了常量级别的额外存储空间,因为只使用了几个整型变量和两个字符串形参,不随着输入数据量的变化而变化。因此,该算法的空间复杂度为 O(1)
kmp 解法
这道题主要还是考察 kmp。上面的暴力解法,一旦不匹配我们是向后移动一位再尝试匹配,而 kmp 则优化了这个移动的过程,向后移动更多位来提高效率。简单来讲,如下图,kmp 是将公共前后缀的前缀移到了后缀的位置而不是像①一样只移动一位位置。
关于 kmp 的理论,建议先看这个视频:【天勤考研】KMP算法易懂版_哔哩哔哩_bilibili,了解下原理。再去看代码随想录的视频熟悉代码该怎么写。

那么每次不匹配的时候该移动多少呢,这就涉及到 next 数组的构建。在进行字符串匹配的时候,我们先构建 next 数组用来记录每个位置的公共前后缀长度,之后当不匹配的时候直接根据 next 数组进行移动。
class Solution {
public:// 获取next数组,用于字符串匹配void getNext(int* next, const string& s) {// ①初始化next数组第一个值为0int j = 0;next[0] = 0; // 循环遍历s中每个字符for(int i = 1; i < s.size(); i++) { // ②前后缀不相同while (j > 0 && s[i] != s[j]) {j = next[j - 1]; //若匹配失败则回溯到之前的状态继续匹配}// ③前后缀相同if (s[i] == s[j]) { //若当前字符和目标匹配j++; //将匹配数量+1}// ④更新next数组next[i] = j; //将新的匹配数量重新赋值至next数组}}// 实现字符串匹配算法int strStr(string haystack, string needle) {int next[needle.size()];getNext(next, needle); //获取needle字符串的next数组int j = 0; //j代表子串needle中已经匹配到的字符个数// 循环遍历haystack中的每个字符for (int i = 0; i < haystack.size(); i++) { while(j > 0 && haystack[i] != needle[j]) {j = next[j - 1]; //回溯,将j移动到目前匹配的最长公共前后缀的结尾处}if (haystack[i] == needle[j]) { //如果当前字符匹配成功j++; //继续匹配下一个字符}if (j == needle.size() ) { //如果匹配成功,返回子串在字符串中的位置return (i - needle.size() + 1);}}return -1; //匹配失败,返回-1}
};
- 时间复杂度:O(m+nm+nm+n)。其中 m 和 n 分别为 haystack 和 needle 字符串的长度。在 strStr 函数中,有一个 while 循环嵌套在 for 循环中,循环次数最多为 haystack 字符串长度 m 加上 needle 字符串长度 n,所以时间复杂度为 O(m+n)
- 空间复杂度:O(nnn)。定义了一个 int 数组 next,其长度为 needle 字符串长度 n,所以空间复杂度为 O(n)
相关文章:

代码随想录刷题-字符串-实现 strStr()
文章目录实现 strStr()习题暴力解法kmp 解法实现 strStr() 本节对应代码随想录中:代码随想录,讲解视频:帮你把KMP算法学个通透!(理论篇)_哔哩哔哩_bilibili、帮你把KMP算法学个通透!࿰…...

前端已死?金三银四?你收到offer了吗?
目录 一、前言 二、“唱衰” 三、不局限于框架、前端 四、打动面试官 五、正向加成 六、小结 一、前言 最近在脉脉、知乎等平台都有人在渲染前端从业人员的危机,甚至使用“前端已死”的字眼,颇有“语不惊人死不休”的意味,对老鸟来说&a…...

C生万物 | 十分钟带你学会位段相关知识
结构体相关知识可以先看看这篇文章 —— 链接 一、什么是位段 位段的声明和结构是类似的,有两个不同: 位段的成员必须是 int、unsigned int 或signed int位段的成员名后边有一个冒号和一个数字 在下面,我分别写了一个结构体和一个位段&…...
Spring Boot基础学习之(十):修改员工的信息
注意:spring boot专栏是一个新手项目,博文顺序则是功能实现的流程,如果有看不懂的内容可以到前面系列去了解。 本次项目所有能够使用的静态资源可以免费进行下载 静态资源 在本篇代码DAO层将通过Java文件去实现,在这里就不连接数…...

闭关十几天,我完成了我的毕业设计
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,也会涉及到服务端(Node.js) 📃个人状态: 在校大学生一枚,已拿多个前端 offer(…...

认识rust的项目管理工具--cargo
cargo 提供了一系列的工具,从项目的建立、构建到测试、运行直至部署,为 Rust 项目的管理提供尽可能完整的手段。不过,我们无需再手动安装,之前安装 Rust 的时候(用rustup或者vscode加插件的方式安装)&#…...
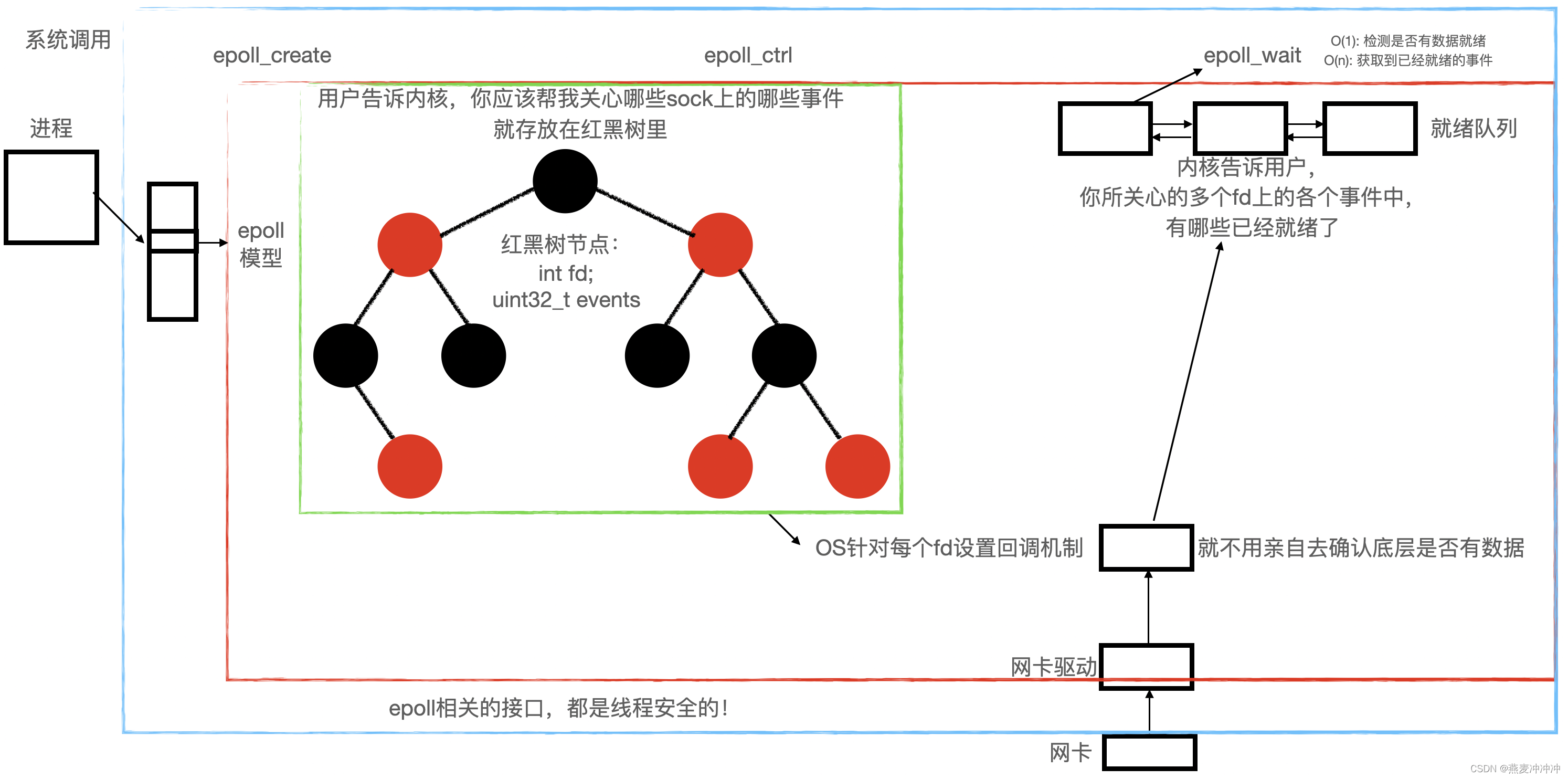
面试常问的Linux之 I/O 复用
I/O 复用 一、I/O的概念 在Linux系统中,I/O(输入/输出)指的是计算机系统的数据交换过程,包括从外部设备读取数据(输入)和将数据发送到外部设备(输出)。I/O操作是Linux系统中非常重要…...

MySQL-binlog+dump备份还原
目录 🍁binlog日志恢复 🍂binlog介绍 🍂Binlog的用途 🍂开启binary log功能 🍂配置binlog 🍁mysqldump 🍂数据库的导出 🍂数据库的导入 🍁mysqldumpbinlog 🦐…...

互联网络-单级互联网络
1.立方体单级网络 1.定义 立方体单级网络(cube)的名称来源于下图所示的三维立方体结构,如010只能连接到000、011、110,不能直接连接到对角线上的001、100、101、111。 2.例题 1.编号为0、1、2、3、4,…,15的16个处理器,用单级互联网络互联,用Cube0互联函数时,与第10…...
上海亚商投顾:沪指四连阳重回3300点 中字头个股再发力
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪大小指数今日走势分化,沪指低开后震荡反弹,创业板指盘中跌超1%。中字头个股再度发力&#x…...

LeetCode:150. 逆波兰表达式求值—栈
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱150. 逆波兰表达式求值 题目描述:给你一个字符串数组 token…...

C/C++每日一练(20230410) 二叉树专场(4)
目录 1. 二叉搜索树迭代器 🌟🌟🌟 2. 验证二叉搜索树 🌟🌟🌟 3. 不同的二叉搜索树 II 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专…...

策化整理1
概述: 本游戏是一款恐怖类解密游戏,以反应毒品的危害和反对家庭暴力为主题 在游戏中玩家扮演被困入梦境内的主人公,寻找逃出梦境的方法 本游戏故事大背景: 主人公的父亲是一名毒贩,在母亲发现父亲开始吸毒后选择与父亲…...
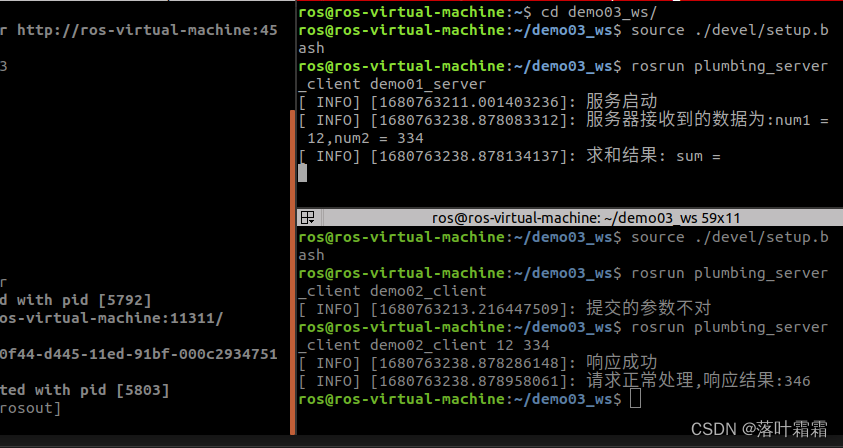
【服务通信自定义srv调用3----客户端的优化】
客户端的优化 服务通信自定义srv调用,客户端随意提交两个数,完成数的相加。也就是实现参数的动态提交: 1.格式:rosrun xxxx xxxx 12 34 2.节点执行时候,需要获取命令中的参数,并且组织进 request 代码中应…...

React跨域解决方案
一、跨域日志报错 我们由于项目需要经常会需要对不同域名、不同子域的网站接口发起请求,有时甚至是对于同一域名的不同端口发起请求,此时我们经常看到以下报错: Access to XMLHttpRequest at xxx from origin xxx has been blocked by COR…...
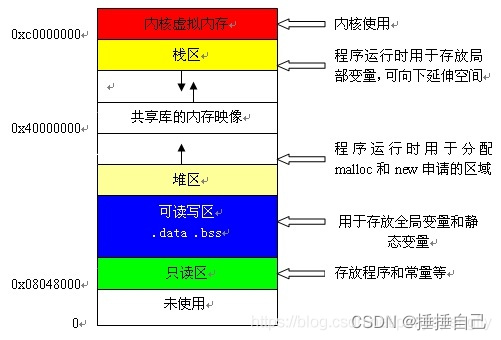
内存五区的概念,内存池技术的诞生。
首先提出一道经典的面试题来引出今天的主角: 进程的虚拟空间分布是什么样的,全局变量放在哪里? 在数据初始化之后,全局变量放在.data段 在数据未初始化时,全局变量放在.bss段 内存五区 进程虚拟内存主要分为五个部分…...

力扣:字符串中的第一个唯一字符(C++实现)
题目部分: 解题思路: 方案一: 首先认真审题的小伙伴们一定会发现就是题目给了提示只包含小写字母,也就是说我们的排查范围是小写的26个字母。为了怕有的友友们一时短路想不起来,我就其按照顺序列出来吧。 即&#x…...

攻防世界 favorite_number mfw、[BJDCTF2020]ZJCTF,不过如此
favorite_number 进入环境得到源码 <?php //php5.5.9 $stuff $_POST["stuff"]; $array [admin, user]; if($stuff $array && $stuff[0] ! admin) {$num $_POST["num"];if (preg_match("/^\d$/im",$num)){if (!preg_match("…...

SummingMergeTree
假设有这样⼀种查询需求:终端⽤户只需要查询数据的汇总结果,不关⼼明细数据,并且数据的汇总条件是预先明确的(GROUP BY 条件明确,且不会随意改变)。 对于这样的查询场景,在ClickHouse中如何解决…...

JUC并发编程基础篇第一章之进程/并发/异步的概念[理解基本概念]
1. 进程和线程的概念 进程: 系统正在运行的一个应用程序;程序一旦运行就是一个进程;进程是资源分配的最小单位 线程: 是进程的实际运行单位;一个人进程可以并发控制多个线程,每条线程并行执行不同的任务 区别: 进程基本上相互独立的;而线程存在于进程内,是进程…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
