C/C++每日一练(20230410) 二叉树专场(4)

目录
1. 二叉搜索树迭代器 🌟🌟🌟
2. 验证二叉搜索树 🌟🌟🌟
3. 不同的二叉搜索树 II 🌟🌟🌟
🌟 每日一练刷题专栏 🌟
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
1. 二叉搜索树迭代器
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:
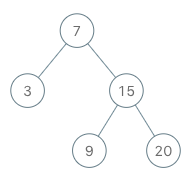
输入 ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] 输出 [null, 3, 7, true, 9, true, 15, true, 20, false] 解释 BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // 返回 3 bSTIterator.next(); // 返回 7 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 9 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 15 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 20 bSTIterator.hasNext(); // 返回 False
提示:
- 树中节点的数目在范围
[1, 10^5]内 0 <= Node.val <= 10^6- 最多调用
10^5次hasNext和next操作
进阶:
- 你可以设计一个满足下述条件的解决方案吗?
next()和hasNext()操作均摊时间复杂度为O(1),并使用O(h)内存。其中h是树的高度。
出处:
https://edu.csdn.net/practice/24633337
代码:
#define null INT_MIN
#include <bits/stdc++.h>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class BSTIterator
{
public:BSTIterator(TreeNode *root){for (; root != nullptr; root = root->left){sti_.push(root);}}/** @return the next smallest number */int next(){TreeNode *smallest = sti_.top();sti_.pop();int val = smallest->val;smallest = smallest->right;for (; smallest != nullptr; smallest = smallest->left){sti_.push(smallest);}return val;}/** @return whether we have a next smallest number */bool hasNext(){return !sti_.empty();}
private:stack<TreeNode *> sti_;
};
/*** Your BSTIterator object will be instantiated and called as such:* BSTIterator* obj = new BSTIterator(root);* int param_1 = obj->next();* bool param_2 = obj->hasNext();*/TreeNode* buildTree(vector<int>& nums)
{if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front());queue<TreeNode*> q;q.push(root);int i = 1;while(!q.empty() && i < nums.size()){TreeNode *cur = q.front();q.pop();if(i < nums.size() && nums[i] != null){cur->left = new TreeNode(nums[i]);q.push(cur->left);}i++;if(i < nums.size() && nums[i] != null){cur->right = new TreeNode(nums[i]);q.push(cur->right);}i++;}return root;
}int main()
{vector<int> nums = {7, 3, 15, null, null, 9, 20};TreeNode *root = buildTree(nums);BSTIterator bSTIterator = BSTIterator(root); cout << bSTIterator.next() << endl; // 返回 3 cout << bSTIterator.next() << endl; // 返回 7 cout << (bSTIterator.hasNext() ? "True" : "False") << endl; // 返回 True cout << bSTIterator.next() << endl; // 返回 9 cout << (bSTIterator.hasNext() ? "True" : "False") << endl; // 返回 True cout << bSTIterator.next() << endl; // 返回 15 cout << (bSTIterator.hasNext() ? "True" : "False") << endl; // 返回 True cout << bSTIterator.next() << endl; // 返回 20 cout << (bSTIterator.hasNext() ? "True" : "False") << endl; // 返回 True return 0;
}
输出:
3
7
True
9
True
15
True
20
False
2. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
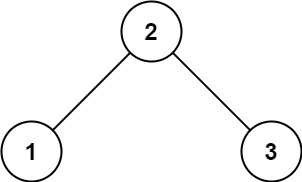
输入:root = [2,1,3] 输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 10^4]内 -2^31 <= Node.val <= 2^31 - 1
以下程序实现了这一功能,请你填补空白处内容:
```c++
#include <bits/stdc++.h>
using namespace std;
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
bool isValidBST(TreeNode *root)
{
stack<TreeNode *> stk;
int prev = INT_MIN;
bool first = true;
while (!stk.empty() || root != nullptr)
{
if (root != nullptr)
{
stk.push(root);
root = root->left;
}
else
{
root = stk.top();
stk.pop();
_______________________;
}
}
return true;
}
};
```
出处:
https://edu.csdn.net/practice/25116236
代码:
#define null INT_MIN
#include <bits/stdc++.h>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution
{
public:bool isValidBST(TreeNode *root){stack<TreeNode *> stk;int prev = INT_MIN;bool first = true;while (!stk.empty() || root != nullptr){if (root != nullptr){stk.push(root);root = root->left;}else{root = stk.top();stk.pop();if (!first && prev >= root->val){return false;}first = false;prev = root->val;root = root->right;}}return true;}
};TreeNode* buildTree(vector<int>& nums)
{if (nums.empty()) return nullptr;TreeNode *root = new TreeNode(nums.front());queue<TreeNode*> q;q.push(root);int i = 1;while(!q.empty() && i < nums.size()){TreeNode *cur = q.front();q.pop();if(i < nums.size() && nums[i] != null){cur->left = new TreeNode(nums[i]);q.push(cur->left);}i++;if(i < nums.size() && nums[i] != null){cur->right = new TreeNode(nums[i]);q.push(cur->right);}i++;}return root;
}int main()
{Solution s;vector<int> nums = {2,1,3};TreeNode* root = buildTree(nums);cout << (s.isValidBST(root) ? "true" : "false") << endl;nums = {5,1,4,null,null,3,6};root = buildTree(nums);cout << (s.isValidBST(root) ? "true" : "false") << endl;return 0;
} 输出:
true
false
3. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:
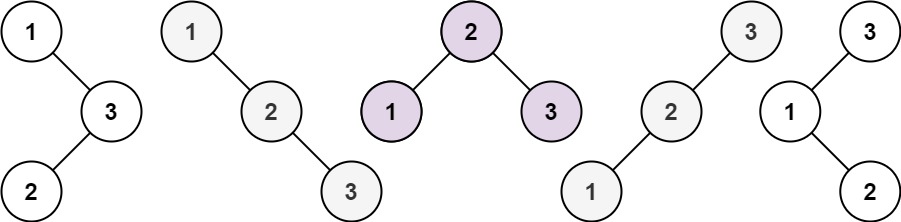
输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 8
代码:
#include <stdio.h>
#include <stdlib.h>struct TreeNode
{int val;struct TreeNode *left;struct TreeNode *right;
};static struct TreeNode *dfs(int low, int high, int *count)
{int i, j, k;if (low > high){*count = 0;return NULL;}else if (low == high){struct TreeNode *node = malloc(sizeof(*node));node->val = low;node->left = NULL;node->right = NULL;*count = 1;return node;}else{*count = 0;int capacity = 5;struct TreeNode *roots = malloc(capacity * sizeof(struct TreeNode));for (i = low; i <= high; i++){int left_cnt, right_cnt;struct TreeNode *left_subs = dfs(low, i - 1, &left_cnt);struct TreeNode *right_subs = dfs(i + 1, high, &right_cnt);if (left_cnt == 0)left_cnt = 1;if (right_cnt == 0)right_cnt = 1;if (*count + (left_cnt * right_cnt) >= capacity){capacity *= 2;capacity += left_cnt * right_cnt;roots = realloc(roots, capacity * sizeof(struct TreeNode));}for (j = 0; j < left_cnt; j++){for (k = 0; k < right_cnt; k++){roots[*count].val = i;roots[*count].left = left_subs == NULL ? NULL : &left_subs[j];roots[*count].right = right_subs == NULL ? NULL : &right_subs[k];(*count)++;}}}return roots;}
}static struct TreeNode **generateTrees(int n, int *returnSize)
{int i, count = 0;struct TreeNode *roots = dfs(1, n, &count);struct TreeNode **results = malloc(count * sizeof(struct TreeNode *));for (i = 0; i < count; i++){results[i] = &roots[i];}*returnSize = count;return results;
}static void dump(struct TreeNode *node)
{printf("%d ", node->val);if (node->left != NULL){dump(node->left);}else{printf("# ");}if (node->right != NULL){dump(node->right);}else{printf("# ");}
}int main(int argc, char **argv)
{if (argc != 2){fprintf(stderr, "Usage: ./test n\n");exit(-1);}int i, count = 0;struct TreeNode **results = generateTrees(atoi(argv[1]), &count);for (i = 0; i < count; i++){dump(results[i]);printf("\n");}return 0;
}略
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
☸ 主页:https://hannyang.blog.csdn.net/
 | Golang每日一练 专栏 |
 | Python每日一练 专栏 |
 | C/C++每日一练 专栏 |
 | Java每日一练 专栏 |
相关文章:

C/C++每日一练(20230410) 二叉树专场(4)
目录 1. 二叉搜索树迭代器 🌟🌟🌟 2. 验证二叉搜索树 🌟🌟🌟 3. 不同的二叉搜索树 II 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专…...

策化整理1
概述: 本游戏是一款恐怖类解密游戏,以反应毒品的危害和反对家庭暴力为主题 在游戏中玩家扮演被困入梦境内的主人公,寻找逃出梦境的方法 本游戏故事大背景: 主人公的父亲是一名毒贩,在母亲发现父亲开始吸毒后选择与父亲…...
【服务通信自定义srv调用3----客户端的优化】
客户端的优化 服务通信自定义srv调用,客户端随意提交两个数,完成数的相加。也就是实现参数的动态提交: 1.格式:rosrun xxxx xxxx 12 34 2.节点执行时候,需要获取命令中的参数,并且组织进 request 代码中应…...

React跨域解决方案
一、跨域日志报错 我们由于项目需要经常会需要对不同域名、不同子域的网站接口发起请求,有时甚至是对于同一域名的不同端口发起请求,此时我们经常看到以下报错: Access to XMLHttpRequest at xxx from origin xxx has been blocked by COR…...
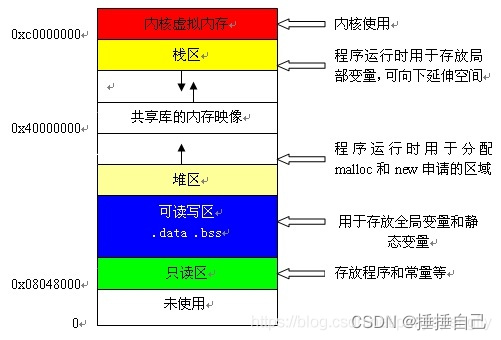
内存五区的概念,内存池技术的诞生。
首先提出一道经典的面试题来引出今天的主角: 进程的虚拟空间分布是什么样的,全局变量放在哪里? 在数据初始化之后,全局变量放在.data段 在数据未初始化时,全局变量放在.bss段 内存五区 进程虚拟内存主要分为五个部分…...

力扣:字符串中的第一个唯一字符(C++实现)
题目部分: 解题思路: 方案一: 首先认真审题的小伙伴们一定会发现就是题目给了提示只包含小写字母,也就是说我们的排查范围是小写的26个字母。为了怕有的友友们一时短路想不起来,我就其按照顺序列出来吧。 即&#x…...

攻防世界 favorite_number mfw、[BJDCTF2020]ZJCTF,不过如此
favorite_number 进入环境得到源码 <?php //php5.5.9 $stuff $_POST["stuff"]; $array [admin, user]; if($stuff $array && $stuff[0] ! admin) {$num $_POST["num"];if (preg_match("/^\d$/im",$num)){if (!preg_match("…...

SummingMergeTree
假设有这样⼀种查询需求:终端⽤户只需要查询数据的汇总结果,不关⼼明细数据,并且数据的汇总条件是预先明确的(GROUP BY 条件明确,且不会随意改变)。 对于这样的查询场景,在ClickHouse中如何解决…...

JUC并发编程基础篇第一章之进程/并发/异步的概念[理解基本概念]
1. 进程和线程的概念 进程: 系统正在运行的一个应用程序;程序一旦运行就是一个进程;进程是资源分配的最小单位 线程: 是进程的实际运行单位;一个人进程可以并发控制多个线程,每条线程并行执行不同的任务 区别: 进程基本上相互独立的;而线程存在于进程内,是进程…...
c语言—指针进阶
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...

总结二分法
杨辉三角形(快速查找唯一值,mid型) //二分法解//流程:最大列->起点行->2k--n之间究竟哪一行(二分排列组合)->找到行数就等差数列对应位置#include<stdio.h> #include<stdlib.h>//注意排列组合的规律是建立在…...
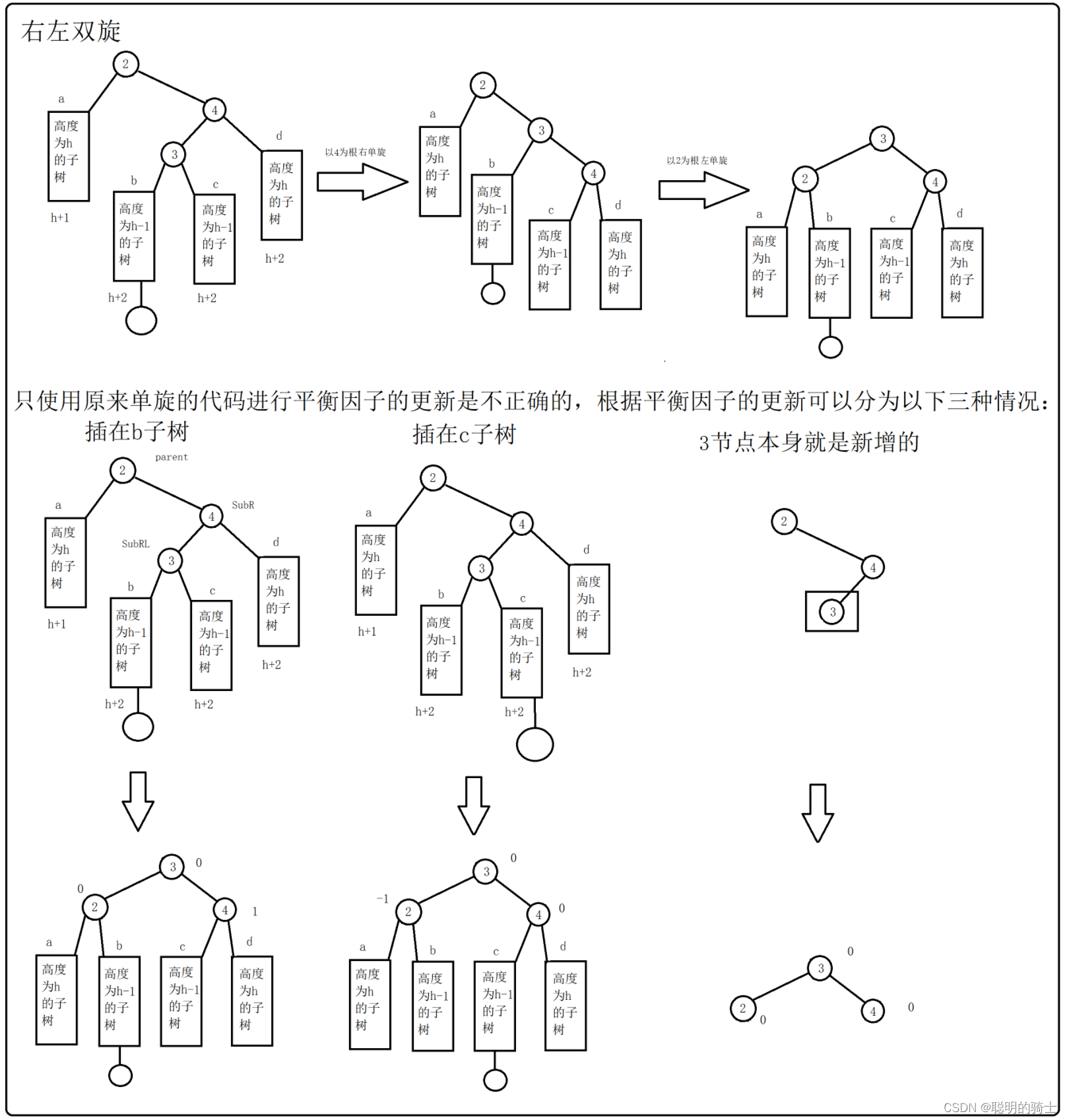
二叉搜索树和AVL树
目录 一、二叉搜索树 1.什么是二叉搜索树 2.二叉搜索树的实现 (1)构建类 (2)查找函数 (3)插入函数 (4)删除函数 (5)补齐默认成员函数 (6…...
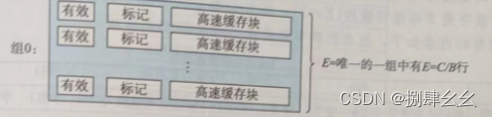
计算机体系结构量化研究方法【2】高速缓存Cache
目录1.计算机存储层次结构2.缓存相关概念3.缓存组织方式4.Cache回写机制5.Cache性能量化1.计算机存储层次结构 计算机存储层次结构可以看作是一个金字塔,越靠上层,容量越小,速度越快 L0:寄存器----CPU的寄存器保存着Cache取出的…...

初识设计模式 - 迭代器模式
简介 迭代器设计模式(Iterator Design Pattern),也叫作游标设计模式(Cursor Design Pattern)。 迭代器模式将集合对象的遍历操作从集合类中拆分出来,放到迭代器类中,让两者的职责更加单一。 …...

三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录 一.前言 二. 三路快排 😍算法思想: 😍算法实现步骤: 😍三指针单趟排序的实现: 😍非递归快排完全体: 🤔与C标准库里的快排进行对比测试: 三.快排时间复杂度再分析 一.前言 http://t.csdn.cn/mz8dghttp://…...

Eyeshot Ultimate 2023 Crack
Eyeshot Ultimate 2023 Crack 已经引入了文档类。 工作区。文档现在包含绘制场景内容所需的所有数据。 2022版GEntities已被删除。 最后,一个真正的跨平台中立核心产品是可用的。 新功能 曲线、平面、曲面和体积网格。 屏幕空间环境光遮挡。 托管ReadDWG和ReadDXF类…...
JAVA-8-[SpringBoot]入门程序案例和原理分析
Spring Boot框架入门教程(快速学习版) Spring Boot教程BooTWiki.COM 1 Spring Boot Spring Boot是Pivotal(关键性的)团队在Spring的基础上提供的一套全新的开源框架,其目的是为了简化Spring应用的搭建和开发过程。Spring Boot去除了大量的X…...

前端工程化
一、AST (抽象语法树,Abstract Syntax Tree) 手把手带你走进Babel的编译世界 - 掘金 (juejin.cn) 1、概念 我们所写的代码转换为机器能识别的一种树形结构,本身是由一堆节点(Node)组成,每个节…...
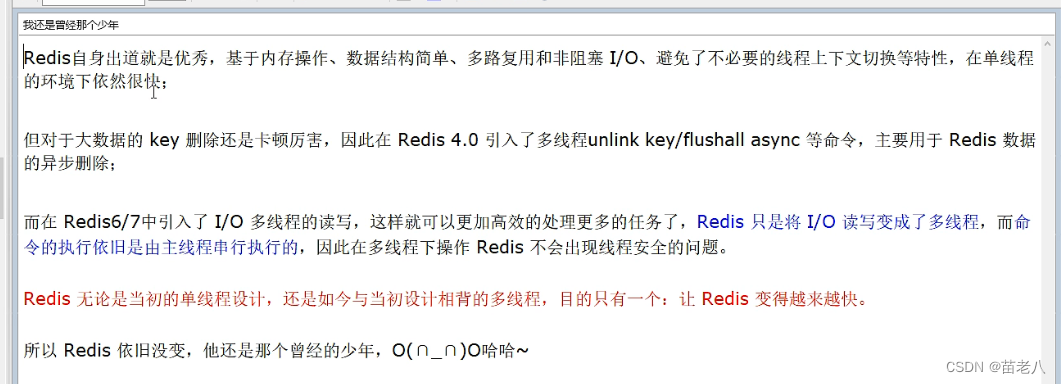
【redis】单线程 VS 多线程(入门)
【redis】单线程 VS 多线程(入门) 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成&#…...

2023蓝桥杯Java研究生组赛题
蓝桥杯Java研究生组、JavaA组看过来,这两个组别题目基本一样 第一次参加了Java研究生组,Java组应该没有C/C那么卷吧,主要是觉得Java组可以避开很多ACM大佬,前面几题感觉难度还行没有特别难,后面几个大题依旧是没法做&a…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
