三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录
一.前言
二. 三路快排
😍算法思想:
😍算法实现步骤:
😍三指针单趟排序的实现:
😍非递归快排完全体:
🤔与C标准库里的快排进行对比测试:
三.快排时间复杂度再分析
一.前言
http://t.csdn.cn/mz8dg
http://t.csdn.cn/mz8dghttp://t.csdn.cn/1TqDp
http://t.csdn.cn/1TqDp
- 😄关于快排的基本思想和实现及其优化
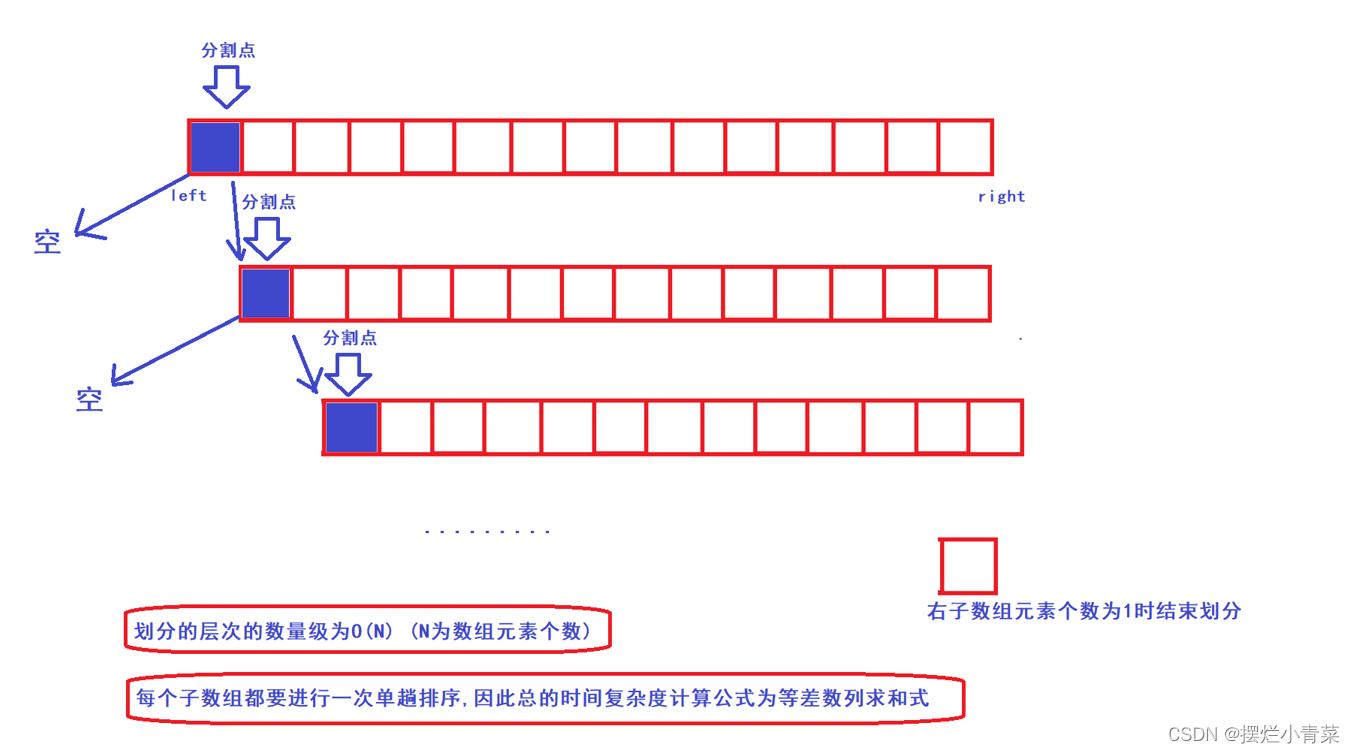
- 😄利用双指针单趟排序实现的快速排序有一个无法避免的缺陷:当待排序序列中有大量(或全部)元素相同时,快排的时间复杂度会升阶为O(N^2),此时快排的递归树呈线型结构,递归的深度为O(N),时间消耗和空间消耗都非常巨大:
- 😄为了避免这种情况出现,就需要重新设计一下快排的单趟排序,目的在于:当待排序序列中存在大量相同元素时,减小快排递归树的深度
二. 三路快排
😍算法思想:
- 🤪三路快排的单趟排序是利用三指针算法来实现的
- 🤪其基本思想是利用三个指针将数组从左到右划分为三个部分,第一部分中所有元素都比key小,第二部分中所有元素都等于key,第三部分中所有元素都大于key
- 🤪后续就可以对数组第一部分和第三部分进行分治,数组的第二部分所有元素已经处于它们在有序序列中的最终位置,无须再进行处理
- 🤪三路快排的边界条件有点折磨人
😍算法实现步骤:
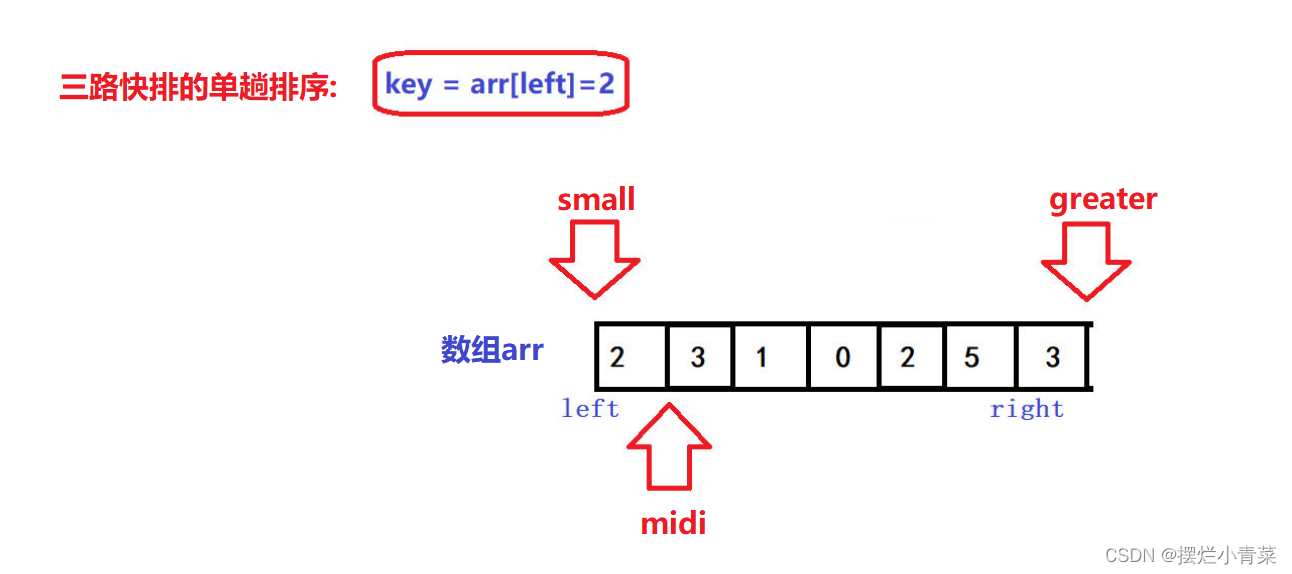
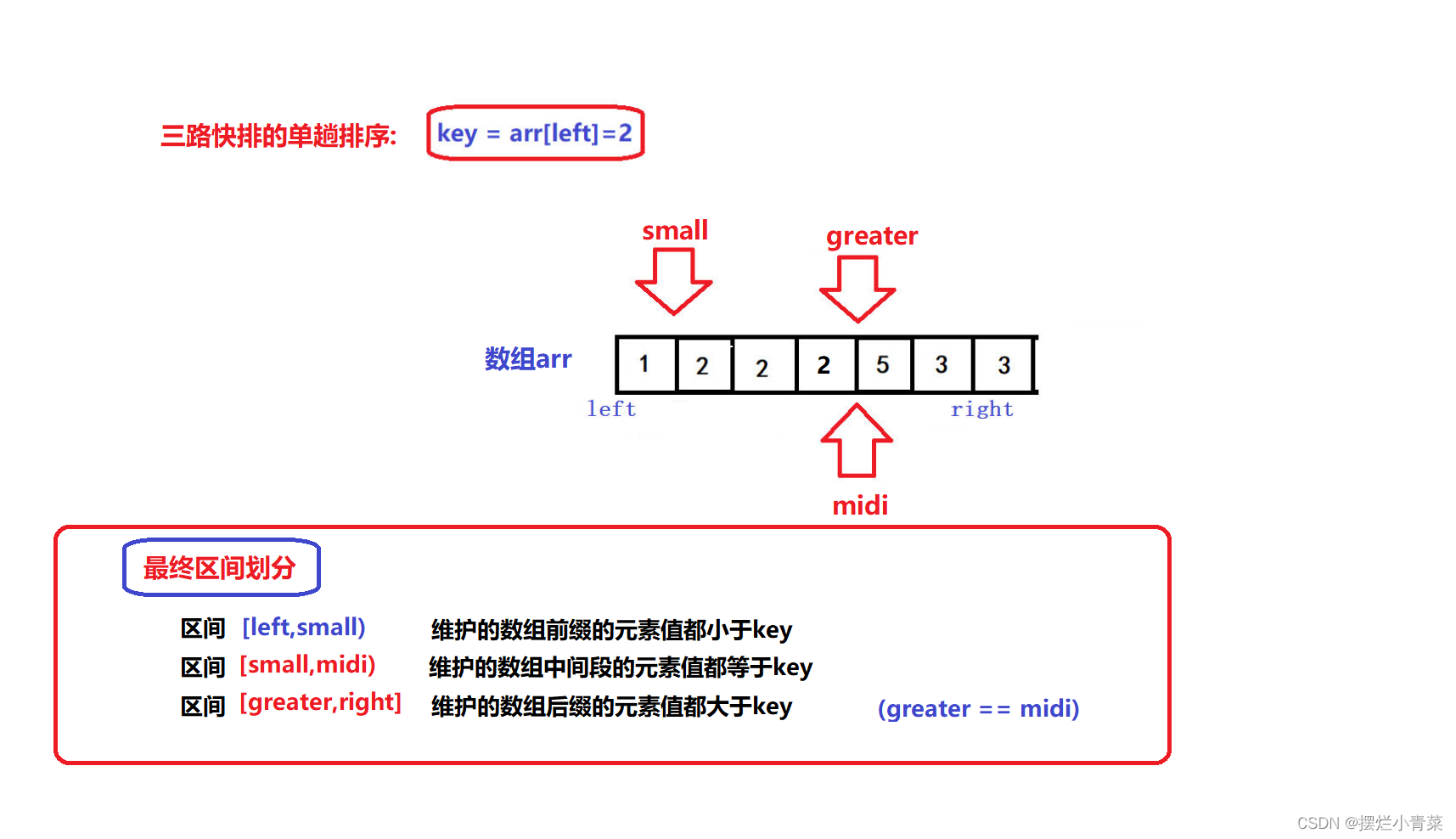
- 🤪三个指针的初始位置如图所示
- 🤪left是待排序区间的左边界,right是待排序区间的右边界,待排序区间为闭区间
- 🤪算法实现思路:
- 🤪利用midi指针来遍历待排序序列,遍历限制条件为:midi<greater.
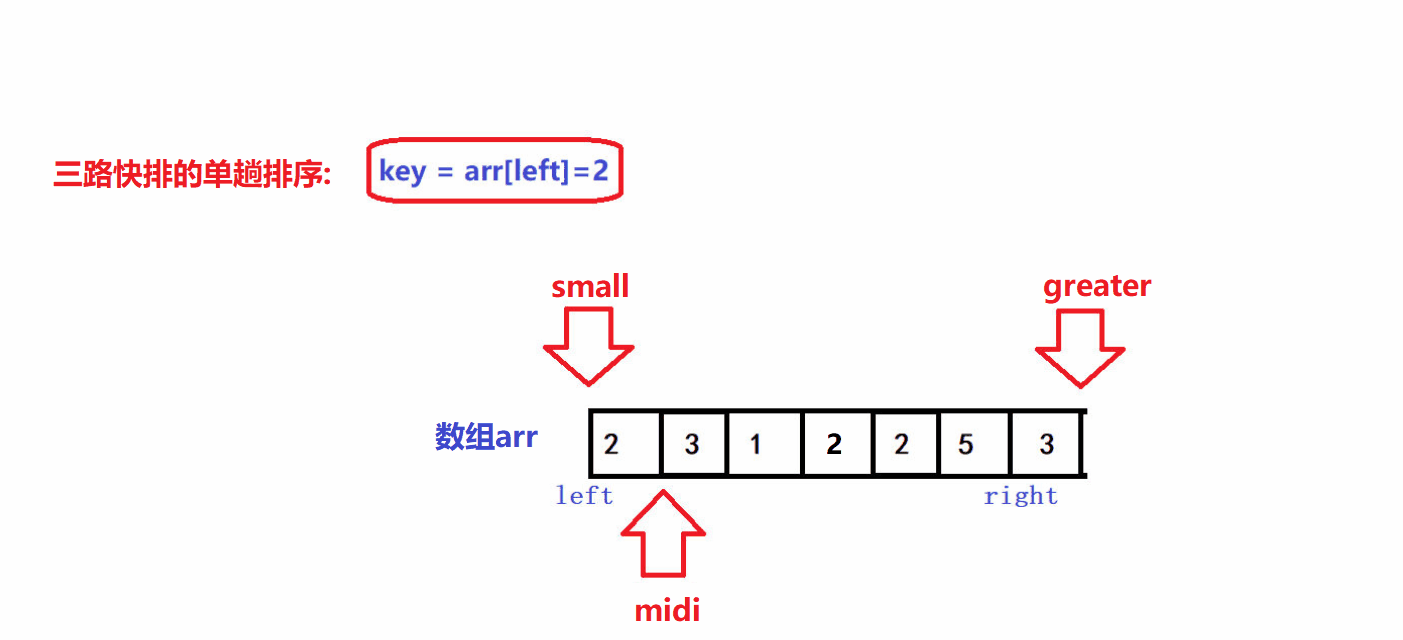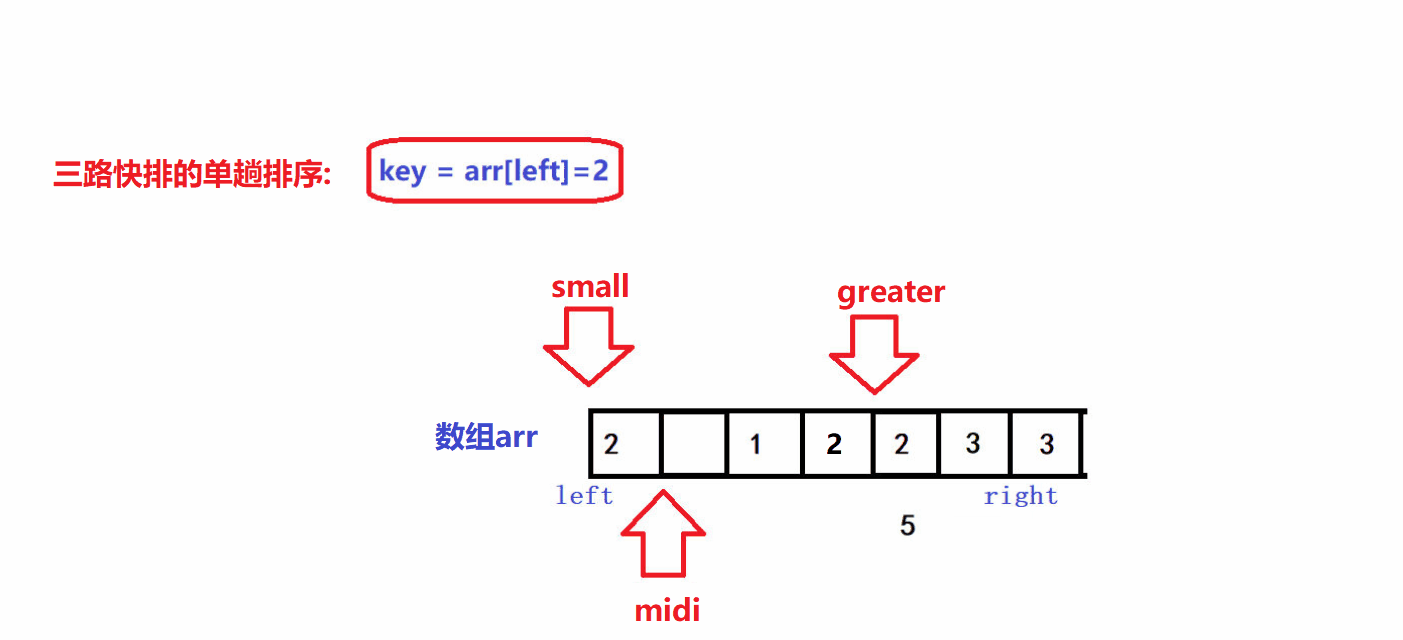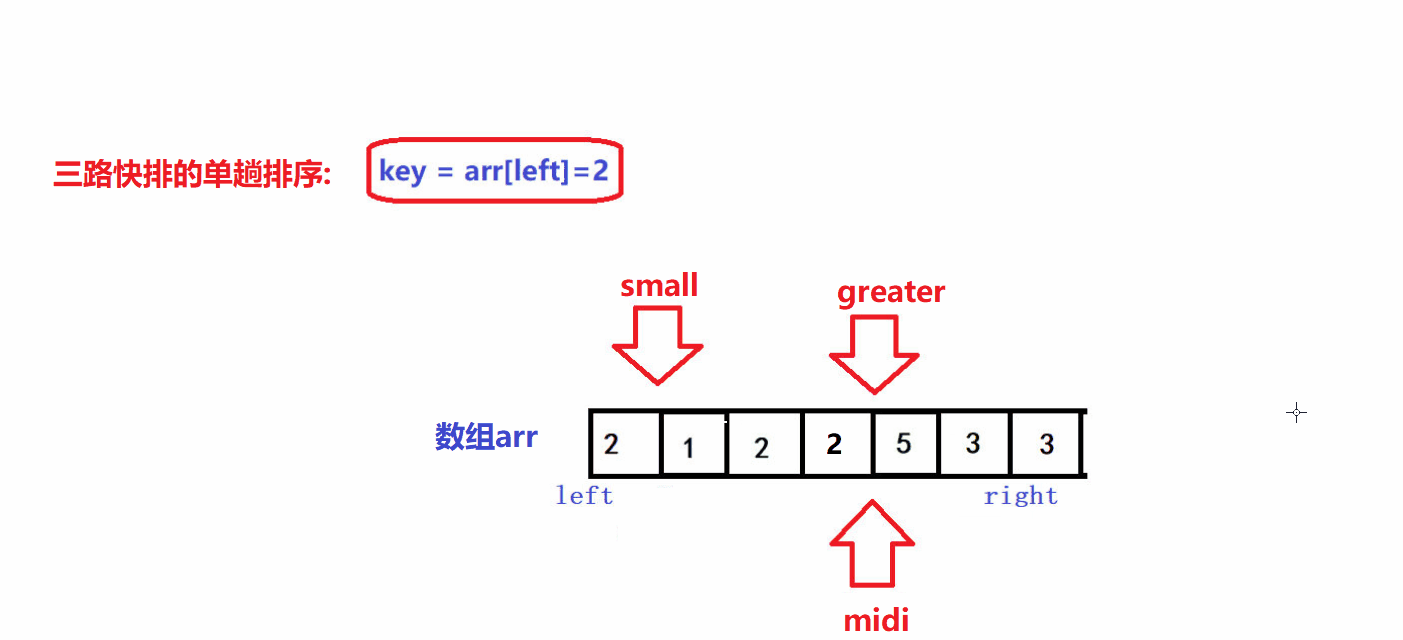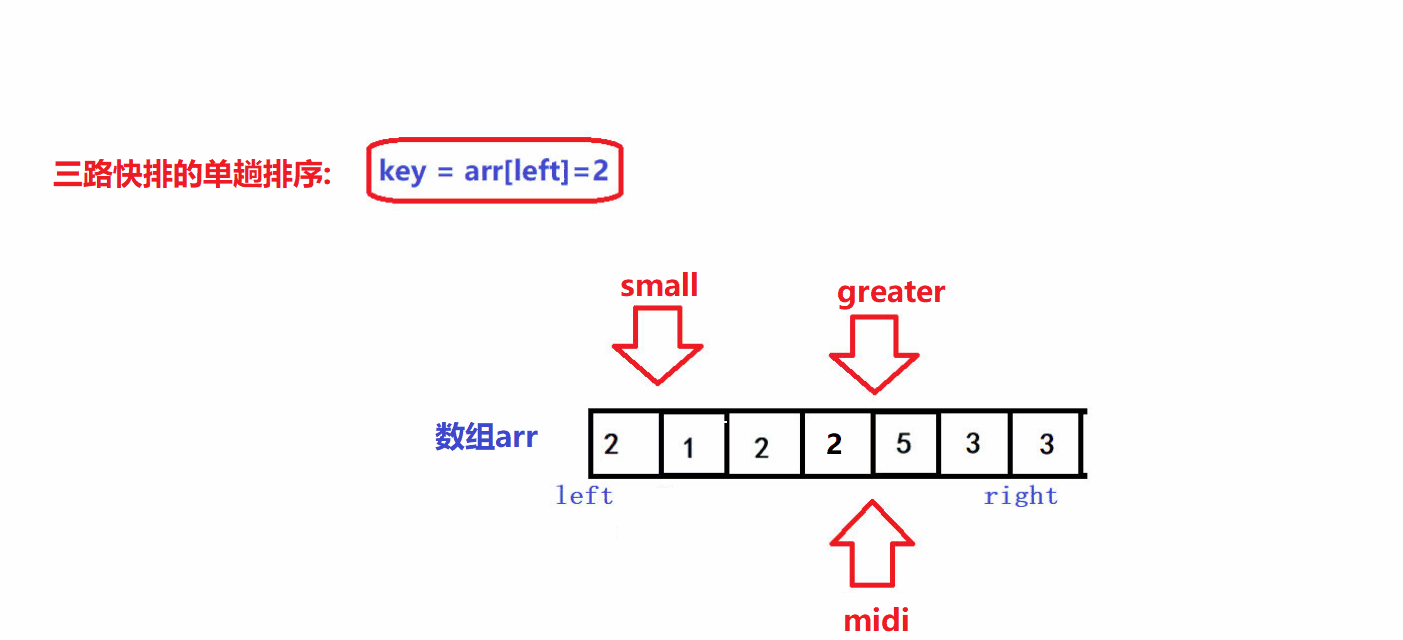
- 😝若arr[midi]比key大,令grater指针减一,并将arr[midi]交换到[greater,right]区间中,midi指针不动
- 😝若arr[midi]比key小,令small指针加一, 并将arr[midi]交换到[left+1,small]区间中,midi指针向前走一步
- 😝若arr[midi]与key相同,midi指针向前走一步,其余指针不动,目的是将等于key元素的arr[midi]"括入"[small+1,midi)区间中
- 😝重复上述过程直到midi指针和geater指针相遇,算法gif:
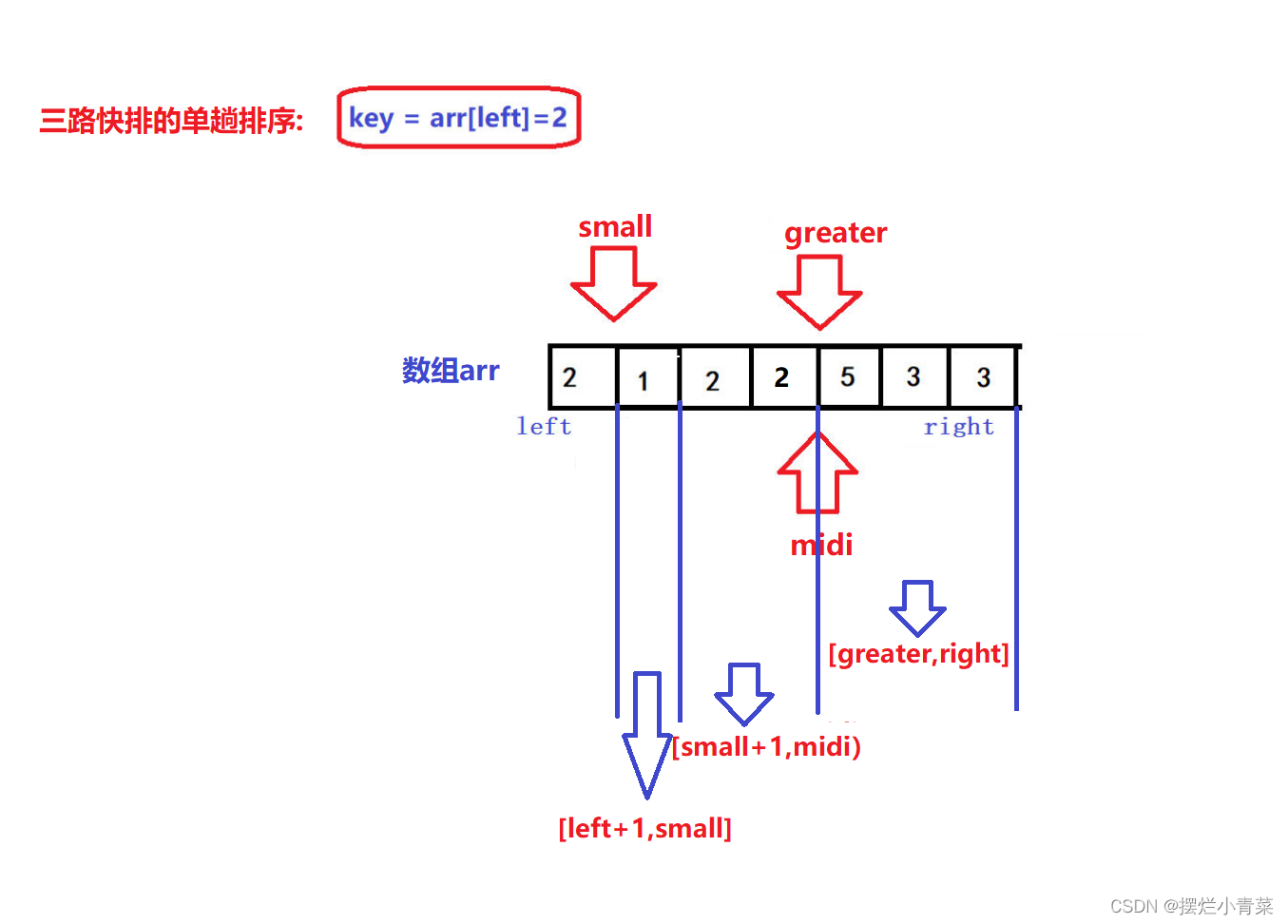
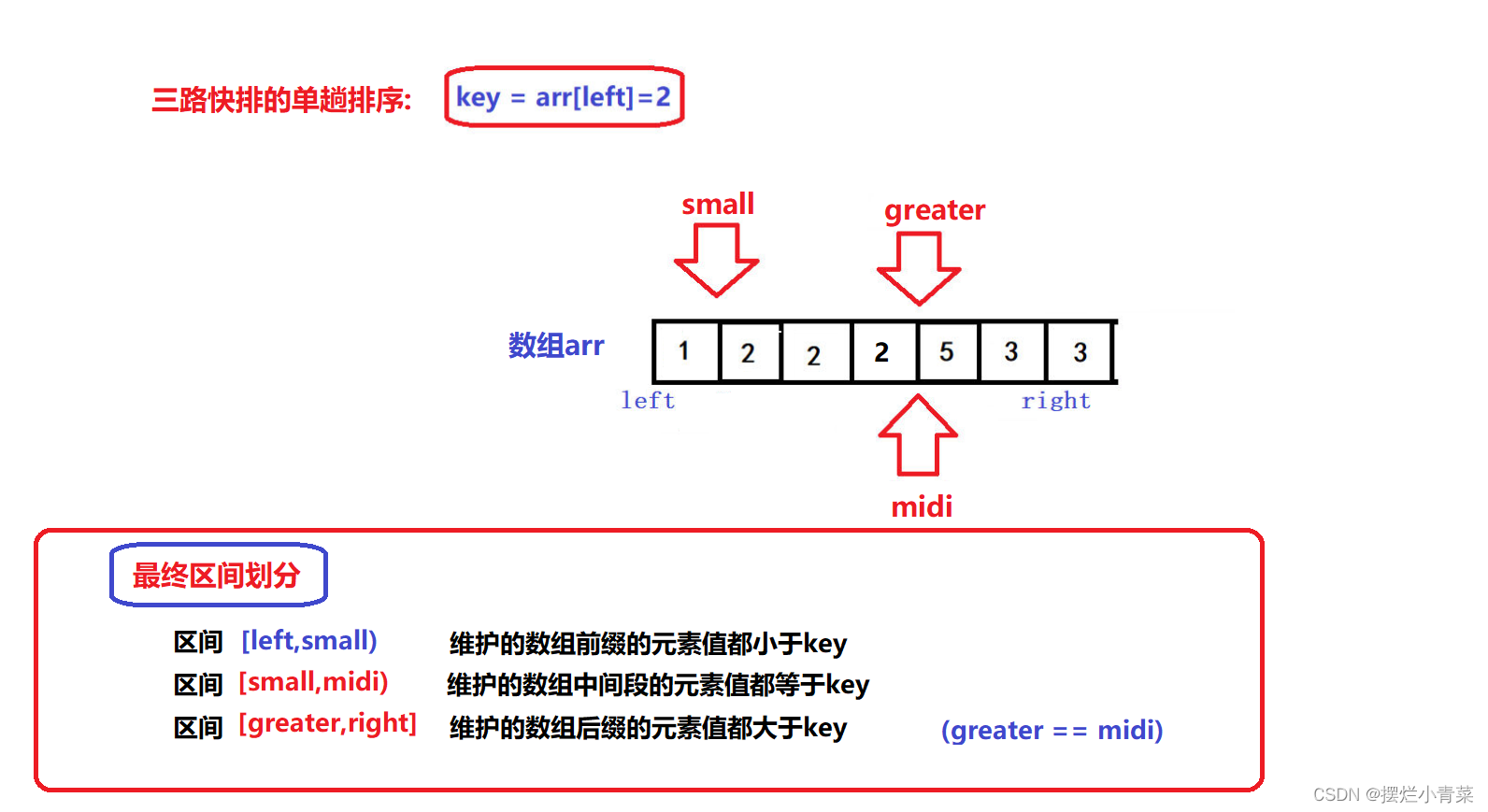
- 😝经过上述过程,最终[left+1,small]区间中的所有元素一定比key小,[greater,right]区间中的所有元素一定比key大,[small+1,midi)区间中的所有元素一定等于key:
- 😝同时注意,迭代过程结束后,small最终指向的元素一定小于key,所以最后一步就是将arr[small]和arr[left]进行交换,于是数组就被划分成了三个部分:
- 😝接下来就可以对区间[left,small-1]和区间[greater,right]进行分治并形成递归完成快速排序
😍三指针单趟排序的实现:
void QuickSort(int* arr, int left, int right) {assert(arr);int key = left;int midi = left + 1;int small = left;int greater = right + 1;while (midi < greater){if (arr[midi] < arr[key]) //将arr[midi]交换到[left + 1, small]区间中,同时注意small位置的元素一定比key元素小{++small;if (small != midi){swap(&arr[small], &arr[midi]);}++midi;}else if (arr[midi] > arr[key]) //将arr[midi]交换到[greater,right]区间{--greater;swap(&arr[midi], &arr[greater]);}else{++midi; //将等于key元素的arr[midi]"括入"[small+1,midi)区间中}}swap(&arr[small], &arr[key]); //small最终指向的元素一定小于key }接下来再进行分治递归并给出递归出口完成快速排序:
😍非递归快排完全体:
- 😝同时辅以三数取中优化
void swap(int* e1, int* e2) {assert(e1 && e2);int tem = *e1;*e1 = *e2;*e2 = tem; }//三数取中优化 int GetMid(int* arr,int left,int right) {int mid = left + ((right - left) >> 2); //在arr[left],arr[mid],arr[right]三者中取中间值作为key,返回key的下标if (arr[left] < arr[right]){if (arr[left] < arr[mid] && arr[mid] < arr[right]){return mid;}else if (arr[mid] > arr[right]){return right;}else{return left;}}else{if (arr[left] > arr[mid] && arr[mid] > arr[right]){return mid;}else if (arr[mid] > arr[left]){return left;}else{return right;}} } void QuickSort(int* arr, int left, int right) {if (left >= right) //递归出口{return;}assert(arr);int key = left;swap(&arr[left], &arr[GetMid(arr, left, right)]);int midi = left + 1;int small = left;int greater = right + 1;while (midi < greater){if (arr[midi] < arr[key]) //将arr[midi]交换到[left + 1, small]区间中,同时注意small位置的元素一定比key元素小{++small;if (small != midi){swap(&arr[small], &arr[midi]);}++midi;}else if (arr[midi] > arr[key]) //将arr[midi]交换到[greater,right]区间{--greater;swap(&arr[midi], &arr[greater]);}else{++midi; //将等于key元素的arr[midi]"括入"[small+1,midi)区间中}}//small指向的元素一定小于keyswap(&arr[small], &arr[key]); //将key交换到其应该出现的最终位置QuickSort(arr, left, small - 1); //分治左子数组QuickSort(arr, midi,right); //分治右子数组 }🤔经过三数取中和三指针优化后的快排就可以对任意序列进行高效排序,不会再出现时间复杂度升阶为O(N^2)的情况
🤔力扣排序测试:(该测试非常针对未经优化和非三指针的快排)
912. 排序数组 - 力扣(Leetcode)
https://leetcode.cn/problems/sort-an-array/description/
🤔与C标准库里的快排进行对比测试:
int main() {srand((unsigned int)time(0));const int N = 10000000;int* arr1 = (int*)malloc(sizeof(int) * N);int* arr2 = (int*)malloc(sizeof(int) * N);int* arr3 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){arr1[i] = rand();arr2[i] = arr1[i];arr3[i] = arr1[i];}int begin2 = clock();qsort(arr2, N, sizeof(int), cmp);int end2 = clock();printf("qsort:%d\n", end2 - begin2);int begin3 = clock();QuickSort(arr3, 0,N-1);int end3 = clock();printf("QuickSort:%d\n", end3 - begin3);free(arr1);free(arr2);free(arr3); }
- 🤔有点奇怪的是在我的机器环境中,我自己写的快排比标准库里的快排还要快一倍左右(可执行程序为release版本)
三.快排时间复杂度再分析
- 😍设N为待排序序列的元素个数
- 😍以下分析中的log都表示以2为底的对数
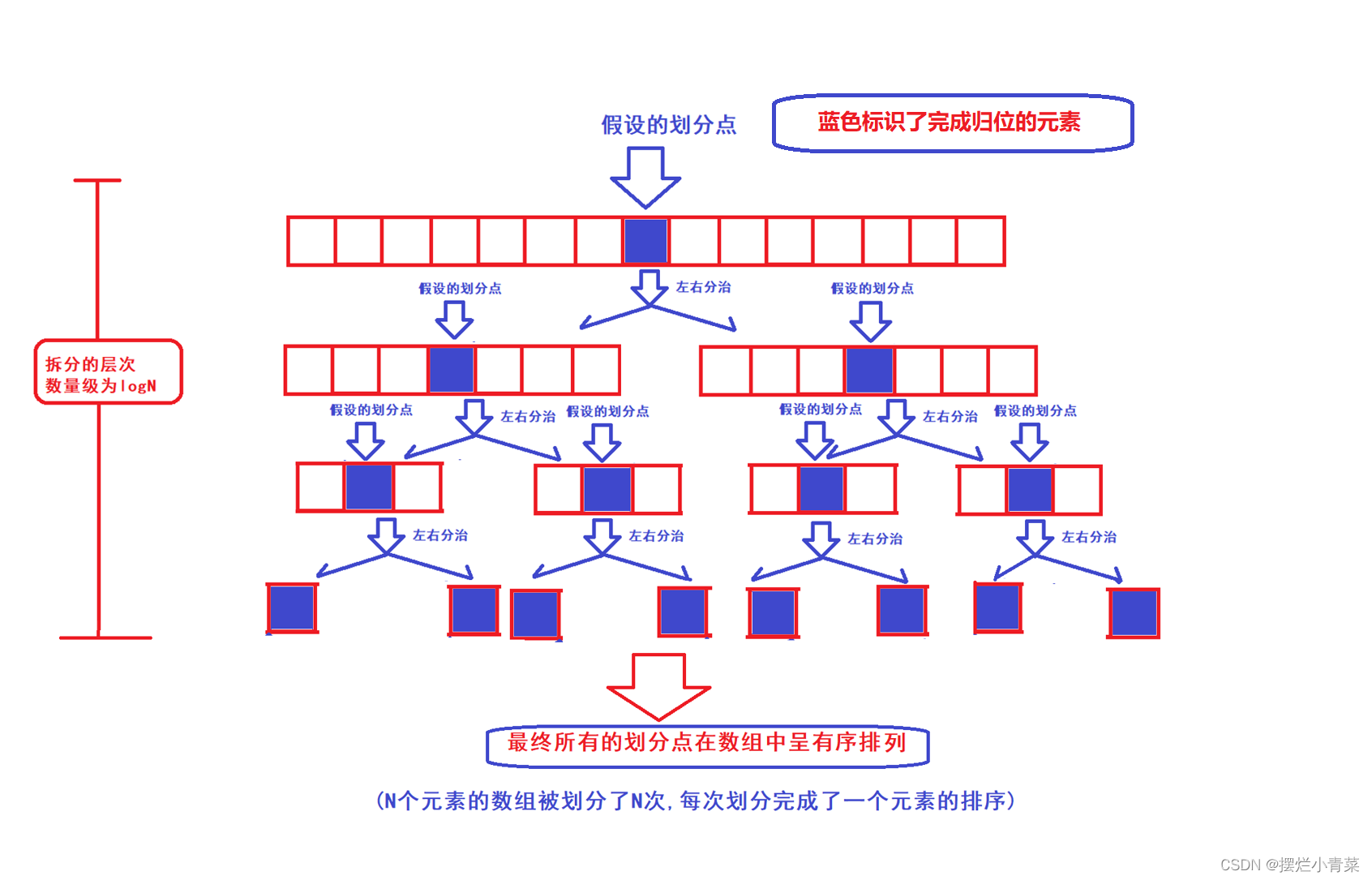
- 😍经过三数取中和三指针优化后的快排分治递归的递归树可以认为在处理任何序列时都接近一颗满二叉树:(注意数组的分割点不参与后续的单趟排序)
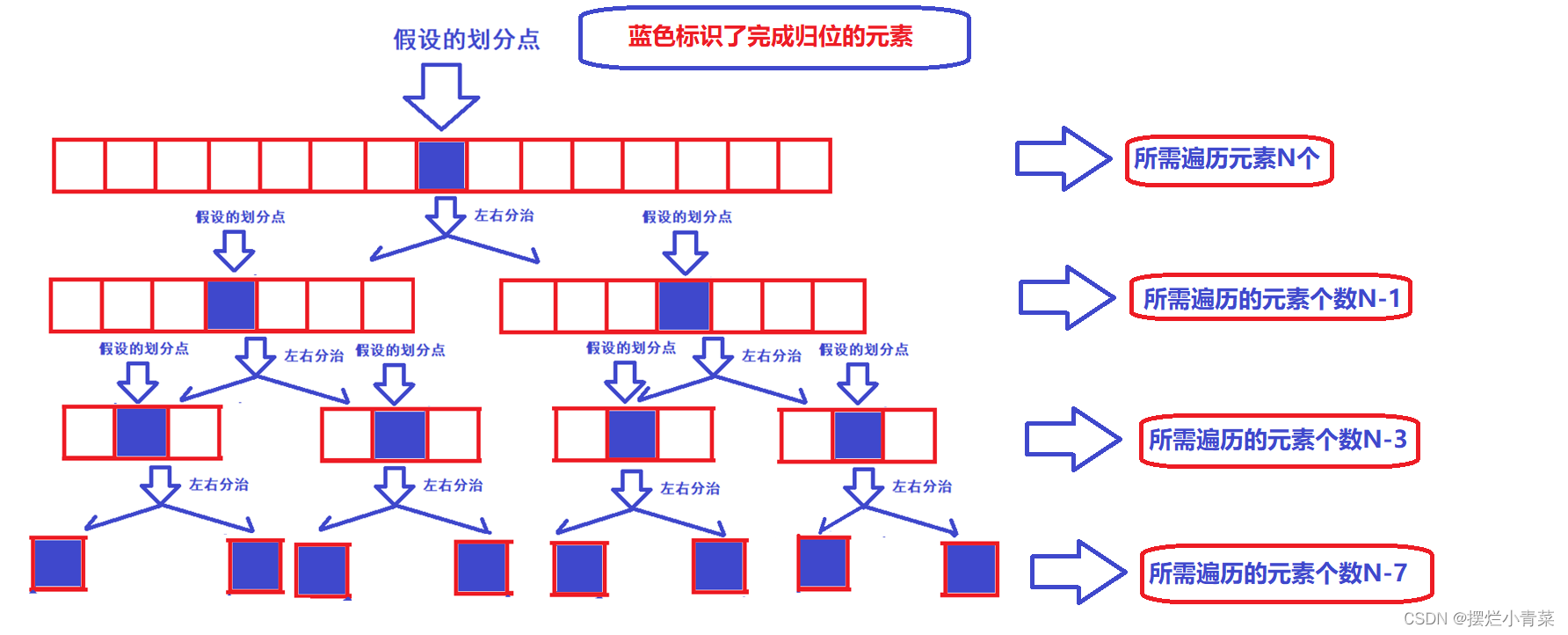
- 😍从递归树的第一层开始,递归树每一层中所有单趟排序所需遍历元素的总个数依次为:N+(N-1)+(N-3)+(N-7)......即快排的时间复杂度计算公式为:
- 😍将上述复杂度公式进行求和运算,取b = logN可得:
- 😍再化简可得:
- 😍可见快速排序的时间复杂度在O(NlogN)的基础上存在进一步的微收敛,这使得快速排序在四个时间复杂度数量级为O(NlogN)的排序算法中独占鳌头进而成为工业级排序中用的最多的排序算法。(四个时间复杂度为O(NlogN)数量级的排序算法分别为:希尔排序,堆排序,归并排序和快速排序)

相关文章:

三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录 一.前言 二. 三路快排 😍算法思想: 😍算法实现步骤: 😍三指针单趟排序的实现: 😍非递归快排完全体: 🤔与C标准库里的快排进行对比测试: 三.快排时间复杂度再分析 一.前言 http://t.csdn.cn/mz8dghttp://…...

Eyeshot Ultimate 2023 Crack
Eyeshot Ultimate 2023 Crack 已经引入了文档类。 工作区。文档现在包含绘制场景内容所需的所有数据。 2022版GEntities已被删除。 最后,一个真正的跨平台中立核心产品是可用的。 新功能 曲线、平面、曲面和体积网格。 屏幕空间环境光遮挡。 托管ReadDWG和ReadDXF类…...
JAVA-8-[SpringBoot]入门程序案例和原理分析
Spring Boot框架入门教程(快速学习版) Spring Boot教程BooTWiki.COM 1 Spring Boot Spring Boot是Pivotal(关键性的)团队在Spring的基础上提供的一套全新的开源框架,其目的是为了简化Spring应用的搭建和开发过程。Spring Boot去除了大量的X…...

前端工程化
一、AST (抽象语法树,Abstract Syntax Tree) 手把手带你走进Babel的编译世界 - 掘金 (juejin.cn) 1、概念 我们所写的代码转换为机器能识别的一种树形结构,本身是由一堆节点(Node)组成,每个节…...
【redis】单线程 VS 多线程(入门)
【redis】单线程 VS 多线程(入门) 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成&#…...

2023蓝桥杯Java研究生组赛题
蓝桥杯Java研究生组、JavaA组看过来,这两个组别题目基本一样 第一次参加了Java研究生组,Java组应该没有C/C那么卷吧,主要是觉得Java组可以避开很多ACM大佬,前面几题感觉难度还行没有特别难,后面几个大题依旧是没法做&a…...

多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测
多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测 目录多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测,CNN-BiLSTM-Atte…...
)
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…...
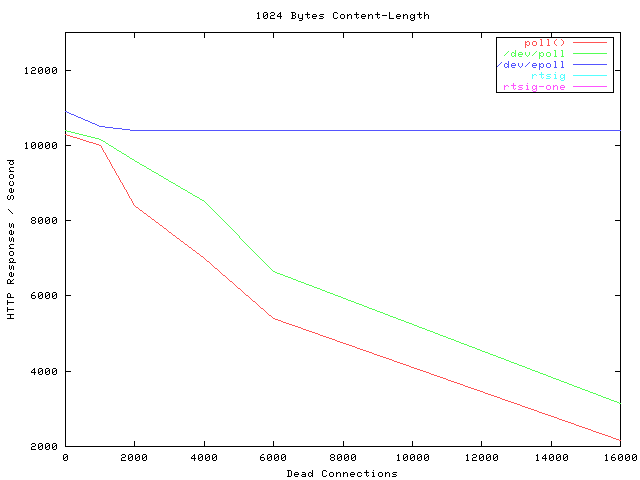
linux内核之select/poll/epoll
一些主流应用IO多路复用技术,突破高并发问题,如nginx、redis、netty,分布式服务框架dubbo,大数据组件hadoop、spark、flink、hbase纷纷使用netty作为网络通信组件。 一、背景:C10K问题 The C10K problem 最早被Dan …...

文件流下载
文件下载 后端传给前端json数据流,前端拿到之后存放在自定义的文件中import axios from "axios"; import qs from "query-string"; import {Notification } from "@arco-design/web-vue"; // 接口中需要含有文件名fileName export function dow…...

C语言模拟实现:atoi函数
在实现atoi之前我们先来了解一下atoi函数的作用是什么: 目录 1.实例演示 2.模拟实现 2.1 判断是否为空指针 2.2判断是否为空字符串 2.3判断正负号 2.4判断非数字字符 2.5判断是否越界 2.6完整代码 1.实例演示 //实例演示 #include <stdio.h> #include …...
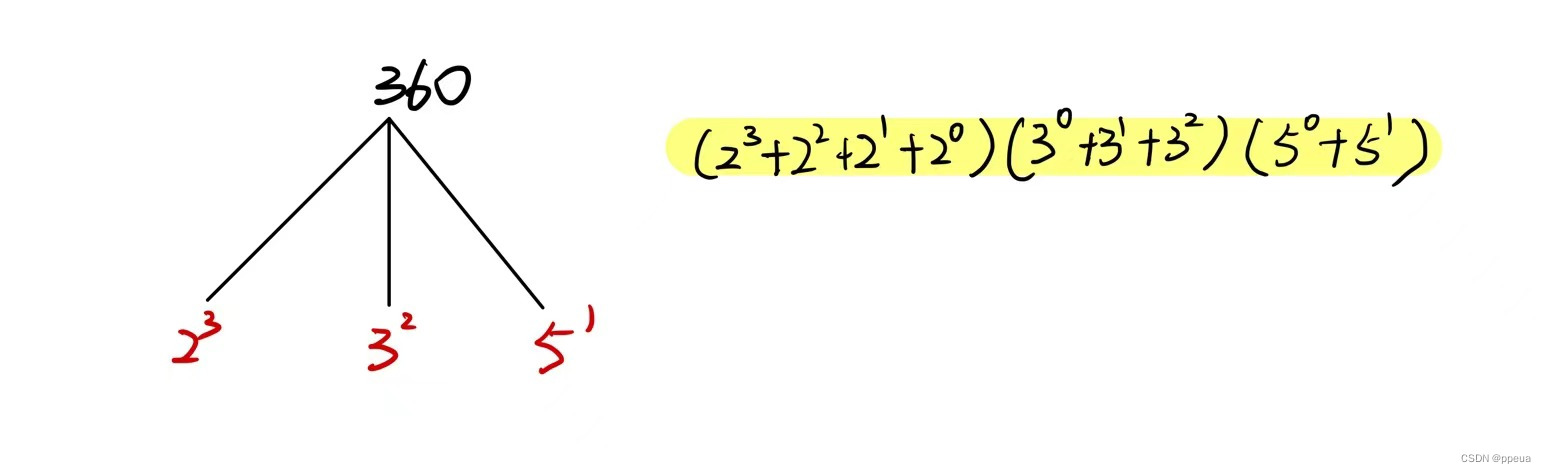
LeetCode.每日一题 2427. 公因子的数目
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
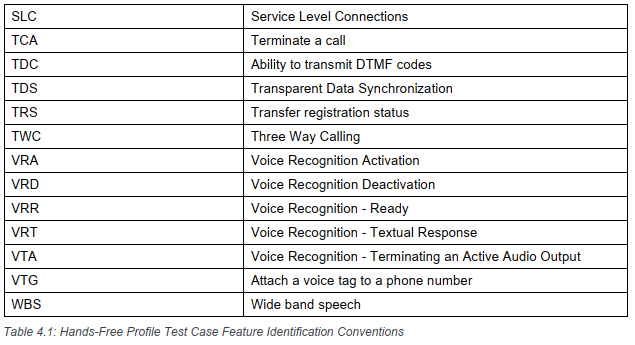
蓝牙BQB认证 - HFP profile配置说明
零.声明 本专栏文章我们会以连载的方式持续更新,本专栏计划更新内容如下: 第一篇:蓝牙综合介绍 ,主要介绍蓝牙的一些概念,产生背景,发展轨迹,市面蓝牙介绍,以及蓝牙开发板介绍。 第二篇:Trans…...
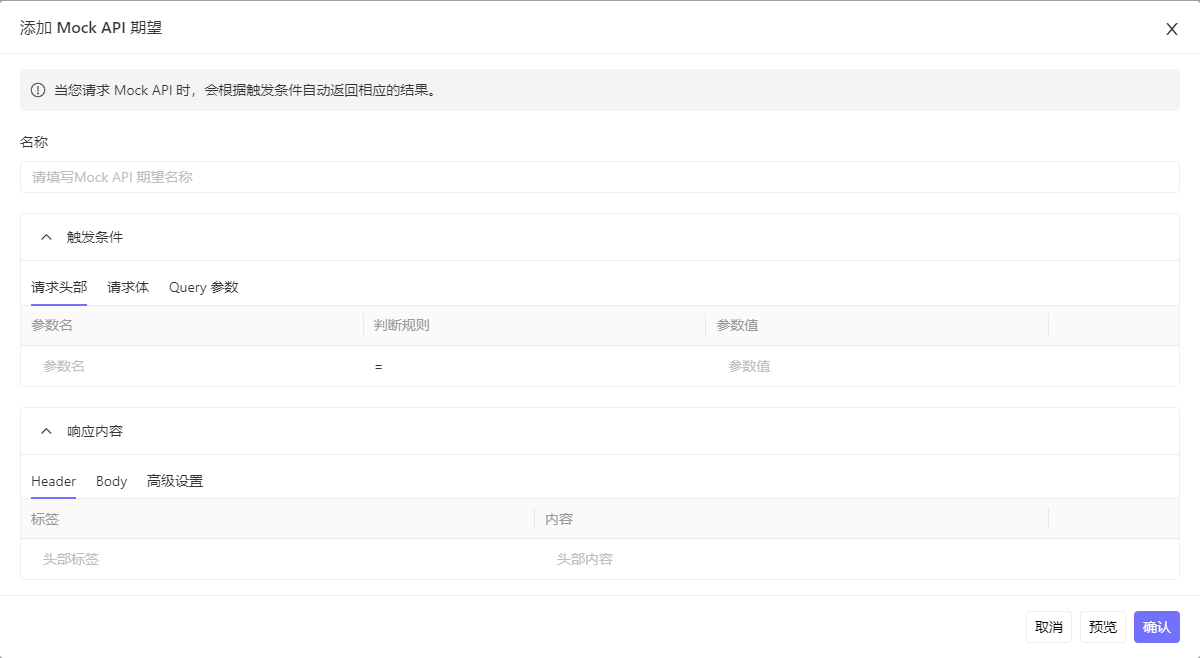
【接口测试工具】Eolink Apikit 快速入门教程
Eolink Apikit 下载安装【官方版】:https://www.eolink.com/apikit 发起 API 测试 进入 API 文档详情页,点击上方 测试 标签,进入 API 测试页,系统会根据 API 文档自动生成测试界面并且填充测试数据。 填写请求参数 首先填写好请…...

使用Python和OpenCV实现实时人脸检测并保存截图
在本篇博客中,我们将使用Python和OpenCV库实现一个实时人脸检测的小项目。我们将利用OpenCV中的Haar级联分类器来检测摄像头捕获的图像中的人脸。 项目功能 通过摄像头实时捕获视频流。使用Haar级联分类器检测视频帧中的人脸。在检测到的人脸周围绘制矩形框。实时…...

[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过
文章目录背景前情回顾描述方法约定MEMCG总览省流总结简介slub 相关 memcg机制kernel 5.9 版本之前结构体初始化具体实现kernel 5.9-5.14kernel 5.14 之后突破slab限制方法cross cache attackpage 堆风水总结背景 前情回顾 关于slab几个结构体的关系和初始化和内存分配和释放的…...
)
MySQL创建数据库(CREATE DATABASE语句)
在 MySQL 中,可以使用 CREATE DATABASE 语句创建数据库,语法格式如下: CREATE DATABASE [IF NOT EXISTS] <数据库名> [[DEFAULT] CHARACTER SET <字符集名>] [[DEFAULT] COLLATE <校对规则名>]; [ ]中的内容是可选的。语…...

【JavaWeb】4—Tomcat
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 如果文章对你有所帮助,可以点赞👍…...
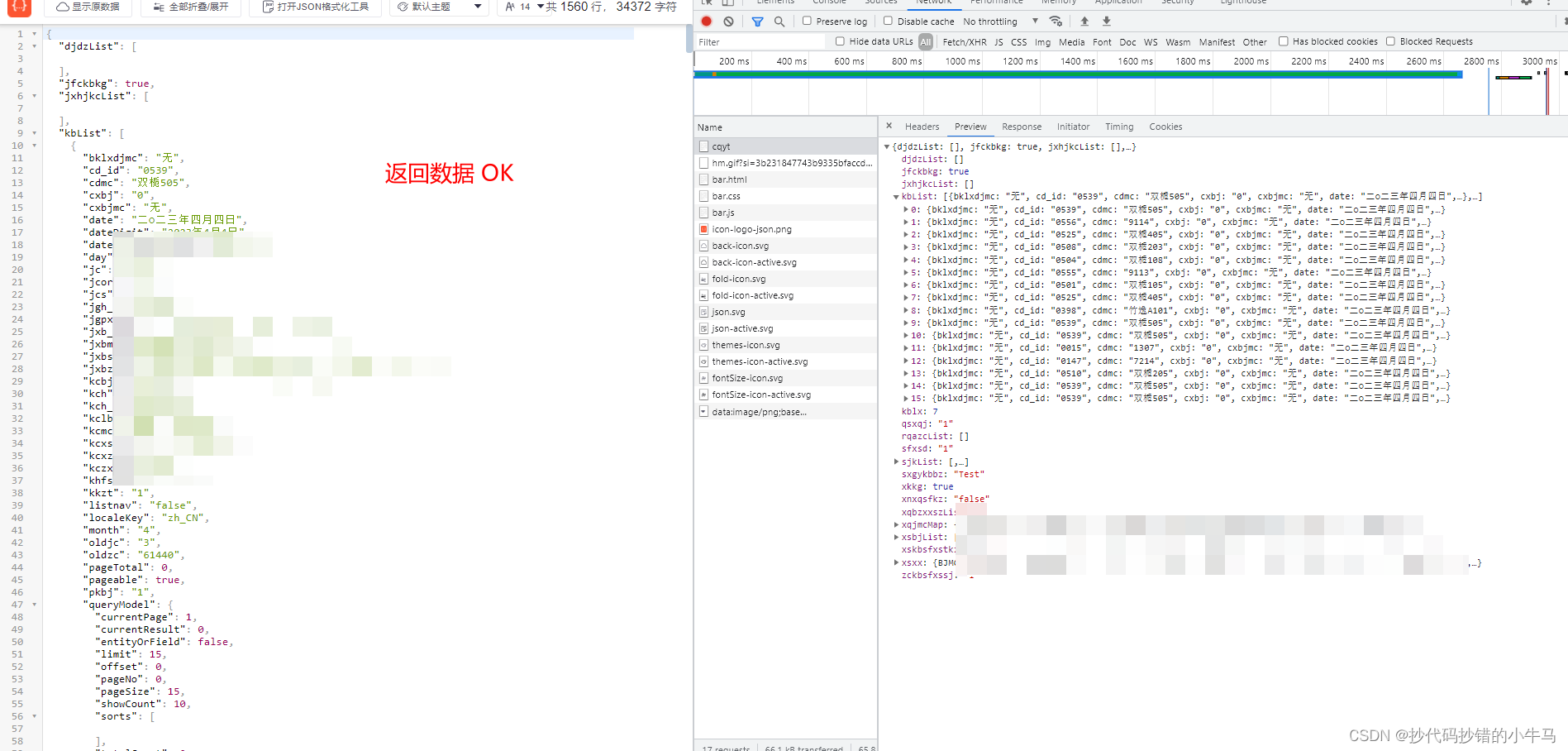
宝塔Linux面板部署Python flask项目
目录 👉1、前言 👉2、安装python项目管理器 👉3、上传项目文件及文件夹 👉4、配置项目 👉5、请求测试 学习记录: 👉1、前言 写在前面:前几天我们实现了外网内外登录正方教务系…...

spring中产生bean的几种方式
BeanImportMyImportSelector implements ImportSelectorMyImportBeanDefinitionRegistarimplements ImportBeanDefinitionRegistrarFactoryBean这里着重讲解FactoryBean如何判断当前bean是否是FactoryBeanorg.springframework.beans.factory.support.AbstractBeanFactory#isFac…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...