总结二分法
杨辉三角形(快速查找唯一值,mid型)
//二分法解//流程:最大列->起点行->2k--n之间究竟哪一行(二分+排列组合)->找到行数就等差数列+对应位置#include<stdio.h>
#include<stdlib.h>//注意排列组合的规律是建立在第0行和第0列的基础!
long C(long a,long b,long n)//C排列组合算法
{long res=1;//一开始要赋值为1!for(long i=a,j=1;j<=b;i--,j++)//一个循环就可以实现C排列组合{res=res*i/j;if(res>n){return res;}//放循环里判断!优化算法//一旦这个res在循环中的结果已经有了超过n的就马上退出,不要再//等它全部遍历完返回再判断!}return res;}int main(int argc, char *argv[]){long n,k;scanf("%ld",&n); // for(k=0;;k++)errfor(k=16;k>=0;k--)//为什么正着输出不行//因为我们是计算第一次出现的数字//那就必须要在最后面的列开始找//一直往前面的列逐个寻找//你从正着遍历就是直接输出最近的也就是第1列//第一列必会出现这个数的答案,因此直接输出了//就不是第一次出现//所以不可以不计算//k代表需要遍历列数//这是根据最大测评数据推出的,1e9//计算器难计算的,就可以借助编程来计算//自己写一个排列组合的函数,该题也用到了这个函数//代数看看最大只可能出现在哪即可//求出最大列数不可能在17列,C17/34大于1e9//因此可以得知在[0,16]之间//k--能写成k++,肌肉记忆是吧?{long l=2*k,r=n;//l等于2k是对应行数//因为一开始从最大列开始算//也就只有2k以后的行才会有这么多的有效列//所以从这以后开始查找//l是需要遍历的行数,//这里等于2k仅仅只是满足最大情况//当最大情况不为所求时就用二分法//矫正行数,这就是为什么二分法只分行数//列不变,也是定一动一.//int mid=(l+r)/2;//这个要放里面,因为每次二分都是不同位置的!while(l<=r) //二分法//二分法可以是mid值作为想要输出的结果//也可以使用right和left作为想要的输出结果//具体不同题设判断如何用l,r还是mid//当结果不用l、r时,我们就不需要考虑//l与r究竟谁赋值mid了。直接舍弃即可(求Mid)//因为我们要求的只有唯一值就是行数//所以可以直接使用mid//直接用mid就是固定的// r=mid-1;// l=mid+1;//类似的模板//(因为既然mid值都不为所求,自然都舍弃)//l是左边界,r是右边界(我们求行数所以左边界为l)//意思就是从l的范围开始找//而r是上限,//所寻找的行永远小于等于n行,所以可以设边界//最差的情况就是数字等于行数//即所找的数字在第n行第二位的情况//所以r=n{long mid=(l+r)/2;//划分中点//我们的二分法是为了寻找所求数字的//所在的行和列,而不是直接找到该数字!if(C(mid,k,n)==n)//mid是所寻找的行不是数字//中点恰好是要找的行//放在全局变量就不用上传这么多参数了{printf("%ld",(1+mid)*mid/2+k+1);//这里是等差数列,每一行的全部是//d=1的等差,1+2+3+......//注意我们求的是数字数量之和不是大小之和//所以(a1+an)*n/2//这里的等差数列是把原来的第0列看成第一列了//这里的等差数列就没有第0列//因此求出来的mid行数就是上一行//恰好可以排等差数列,剩下的加上k+1即可//k+1是因为排列组合有第0列,既然是在使用这个//规律的基础上,就必须遵循第0列开始,//而第0列->k列就是k+1//注意过程的选取,是等差数列的过程// 还是处在排列组合的过程return 0;}else if(C(mid,k,n)>n)r=mid-1;//mid太大就只可能在左边一堆,//然后循环再分一次else//mid太小l=mid+1;}}return 0;
}递增三元组(求极限/多种情况最优最佳结果,l、r型)
#include<bits/stdc++.h>//递增三元组using namespace std;
int main()
{int a[100000],b[100000],c[100000];int n;long long ans=0;cin>>n;for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<n;i++)cin>>b[i];for(int i=0;i<n;i++)cin>>c[i];sort(a,a+n);//直接写出首尾就ok了sort(c,c+n);int left,right;
for(int i=0;i<n;i++)//枚举b
{//找出比b小的最大的a,比b大的最小的cleft=0,right=n-1;while(left<right){int mid=(left+right+1)/2;if(b[i]<=a[mid])//当前a的值大于等于b,我也不要了//a太大,我就缩小//注意,这个小于等于要放在一起因为都归为mid不可取的一边//如果只写<,那么等于在下面就无法把等于这种情况去除.right=mid-1;elseleft=mid;//当前mid满足条件可取}int x=right;left=0,right=n-1;
while(left<right)
{int mid=(left+right)/2;if(b[i]>=c[mid])//条件不满足题意,mid值不要left=mid+1;elseright=mid;//符合,mid可取}
int y=right;if(a[x]<b[i]&&b[i]<c[y])
{// ans+=(x+1)*(n-y);errans+=(long long)(x+1)*(n-y);//两个相乘是因为排列组合//定下1个b,每一种的a都有n-y个c的情况.//一个数据错了,这里相乘计算大数据会溢出//所以要扩大数据类型!//但是给x,y修改类型竟然也能过,我不知道为什么//但逻辑来讲还是改这里的数据类型比较严谨
}}cout<<ans;return 0;
}总结:
如果二分法输出的是l、r,那么循环搜索的原理就是当l==r时结束搜索
此时l与r的值都是一样的,都能作为结果输出
循环条件为l<r
等于时就停止循环了,不要写l<=r不然会死循环
而mid作为结果输出时
我不关心l、r的结果
我要求的是mid,而l==r时,同样仍然还可以再求中间值
如果是这种情况也就是mid==l==r
那么也要将这个结果赋值给mid,要不然你的mid也是错的
因此求mid时条件为l<=r
求mid的二分的前提是找一个值,是相当于只是优化算法
加快了遍历速度,就是每次都遍历一半,其实完全可以用for循环暴力遍历
当前是唯一值,线性的范围内,只要这个mid符合条件我就马上退出循环了
不满足就继续分
这个是查找唯一的下标值
而求l、r是不同的,这个二分相当于是求一个边界和极限
因为l、r可以不断移动,所以是通过调整l、r的位置来确定唯一的值
当l==r时,就是那个划分边界的点,此时的mid只是作为调位的一个工具
初始的时候l、r距离很大,后来不断二分缩小他们的位置,最后相等时
即确定了极限和边界位置.
求l、r的时候才真正体现了二分的优越性.
mid更像是快速查找唯一值,而l、r则似求一个满足当前条件的一个极限值
明显的特征就是l、r的情况有多个结果,只是在多个结果中挑选出一个
最佳最优的情况,也就是极限,就要用l、r来收缩求最佳结果.
相关文章:

总结二分法
杨辉三角形(快速查找唯一值,mid型) //二分法解//流程:最大列->起点行->2k--n之间究竟哪一行(二分排列组合)->找到行数就等差数列对应位置#include<stdio.h> #include<stdlib.h>//注意排列组合的规律是建立在…...
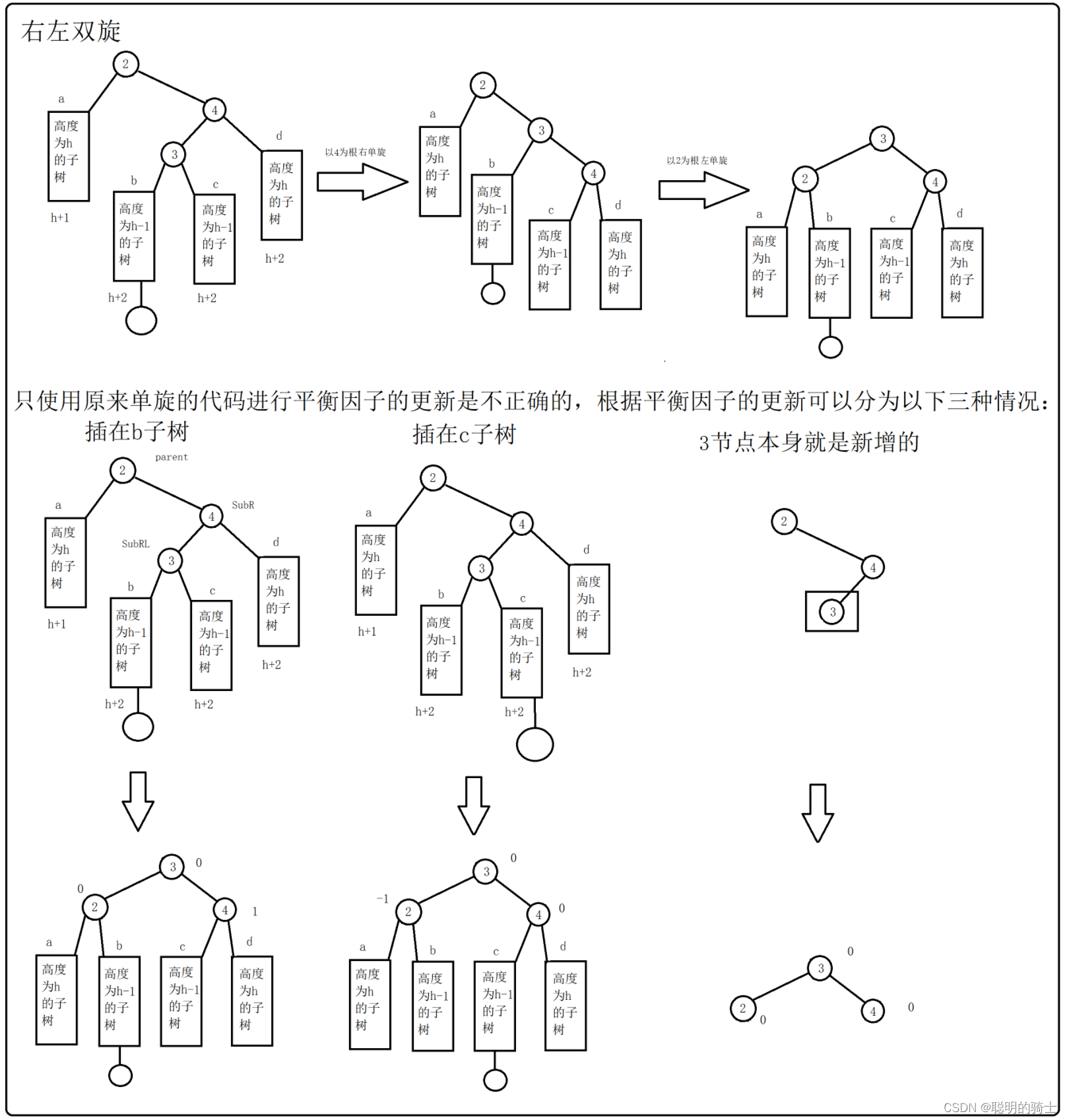
二叉搜索树和AVL树
目录 一、二叉搜索树 1.什么是二叉搜索树 2.二叉搜索树的实现 (1)构建类 (2)查找函数 (3)插入函数 (4)删除函数 (5)补齐默认成员函数 (6…...
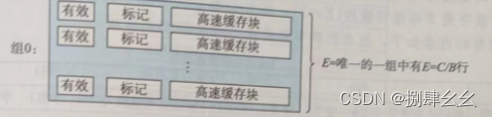
计算机体系结构量化研究方法【2】高速缓存Cache
目录1.计算机存储层次结构2.缓存相关概念3.缓存组织方式4.Cache回写机制5.Cache性能量化1.计算机存储层次结构 计算机存储层次结构可以看作是一个金字塔,越靠上层,容量越小,速度越快 L0:寄存器----CPU的寄存器保存着Cache取出的…...

初识设计模式 - 迭代器模式
简介 迭代器设计模式(Iterator Design Pattern),也叫作游标设计模式(Cursor Design Pattern)。 迭代器模式将集合对象的遍历操作从集合类中拆分出来,放到迭代器类中,让两者的职责更加单一。 …...

三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录 一.前言 二. 三路快排 😍算法思想: 😍算法实现步骤: 😍三指针单趟排序的实现: 😍非递归快排完全体: 🤔与C标准库里的快排进行对比测试: 三.快排时间复杂度再分析 一.前言 http://t.csdn.cn/mz8dghttp://…...

Eyeshot Ultimate 2023 Crack
Eyeshot Ultimate 2023 Crack 已经引入了文档类。 工作区。文档现在包含绘制场景内容所需的所有数据。 2022版GEntities已被删除。 最后,一个真正的跨平台中立核心产品是可用的。 新功能 曲线、平面、曲面和体积网格。 屏幕空间环境光遮挡。 托管ReadDWG和ReadDXF类…...
JAVA-8-[SpringBoot]入门程序案例和原理分析
Spring Boot框架入门教程(快速学习版) Spring Boot教程BooTWiki.COM 1 Spring Boot Spring Boot是Pivotal(关键性的)团队在Spring的基础上提供的一套全新的开源框架,其目的是为了简化Spring应用的搭建和开发过程。Spring Boot去除了大量的X…...

前端工程化
一、AST (抽象语法树,Abstract Syntax Tree) 手把手带你走进Babel的编译世界 - 掘金 (juejin.cn) 1、概念 我们所写的代码转换为机器能识别的一种树形结构,本身是由一堆节点(Node)组成,每个节…...
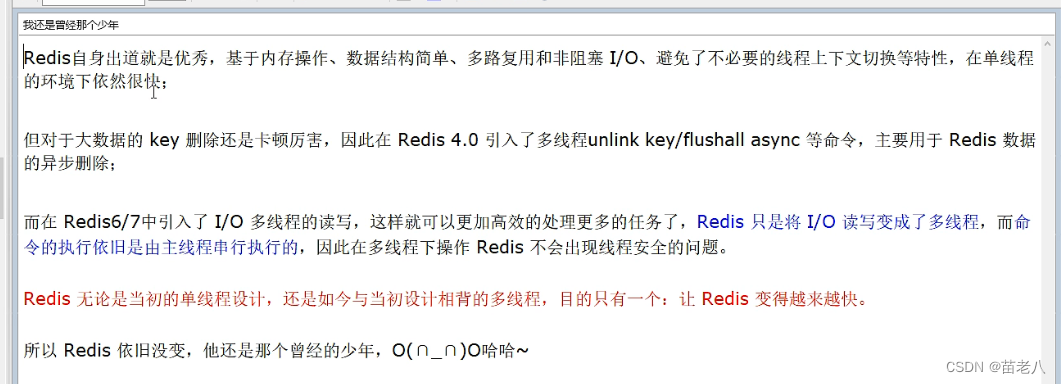
【redis】单线程 VS 多线程(入门)
【redis】单线程 VS 多线程(入门) 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成&#…...

2023蓝桥杯Java研究生组赛题
蓝桥杯Java研究生组、JavaA组看过来,这两个组别题目基本一样 第一次参加了Java研究生组,Java组应该没有C/C那么卷吧,主要是觉得Java组可以避开很多ACM大佬,前面几题感觉难度还行没有特别难,后面几个大题依旧是没法做&a…...

多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测
多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测 目录多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测,CNN-BiLSTM-Atte…...
)
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…...
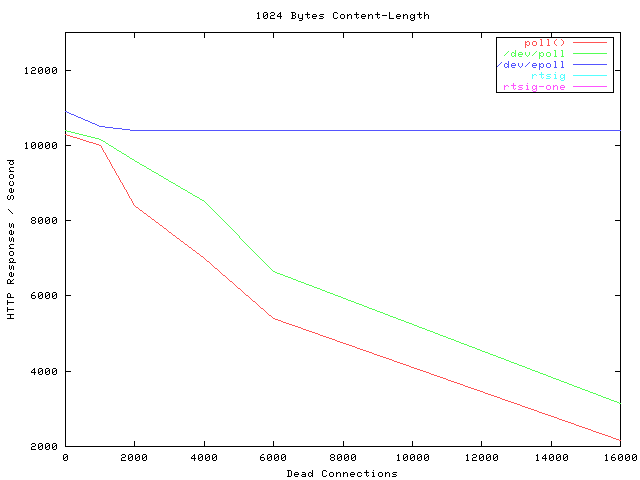
linux内核之select/poll/epoll
一些主流应用IO多路复用技术,突破高并发问题,如nginx、redis、netty,分布式服务框架dubbo,大数据组件hadoop、spark、flink、hbase纷纷使用netty作为网络通信组件。 一、背景:C10K问题 The C10K problem 最早被Dan …...

文件流下载
文件下载 后端传给前端json数据流,前端拿到之后存放在自定义的文件中import axios from "axios"; import qs from "query-string"; import {Notification } from "@arco-design/web-vue"; // 接口中需要含有文件名fileName export function dow…...

C语言模拟实现:atoi函数
在实现atoi之前我们先来了解一下atoi函数的作用是什么: 目录 1.实例演示 2.模拟实现 2.1 判断是否为空指针 2.2判断是否为空字符串 2.3判断正负号 2.4判断非数字字符 2.5判断是否越界 2.6完整代码 1.实例演示 //实例演示 #include <stdio.h> #include …...
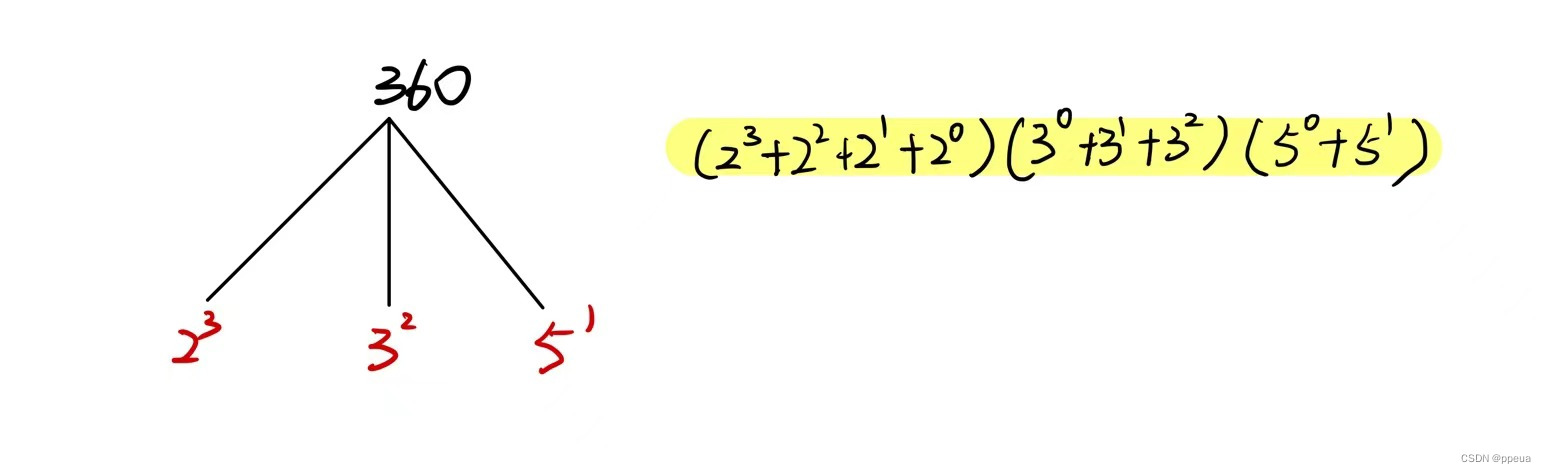
LeetCode.每日一题 2427. 公因子的数目
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
蓝牙BQB认证 - HFP profile配置说明
零.声明 本专栏文章我们会以连载的方式持续更新,本专栏计划更新内容如下: 第一篇:蓝牙综合介绍 ,主要介绍蓝牙的一些概念,产生背景,发展轨迹,市面蓝牙介绍,以及蓝牙开发板介绍。 第二篇:Trans…...
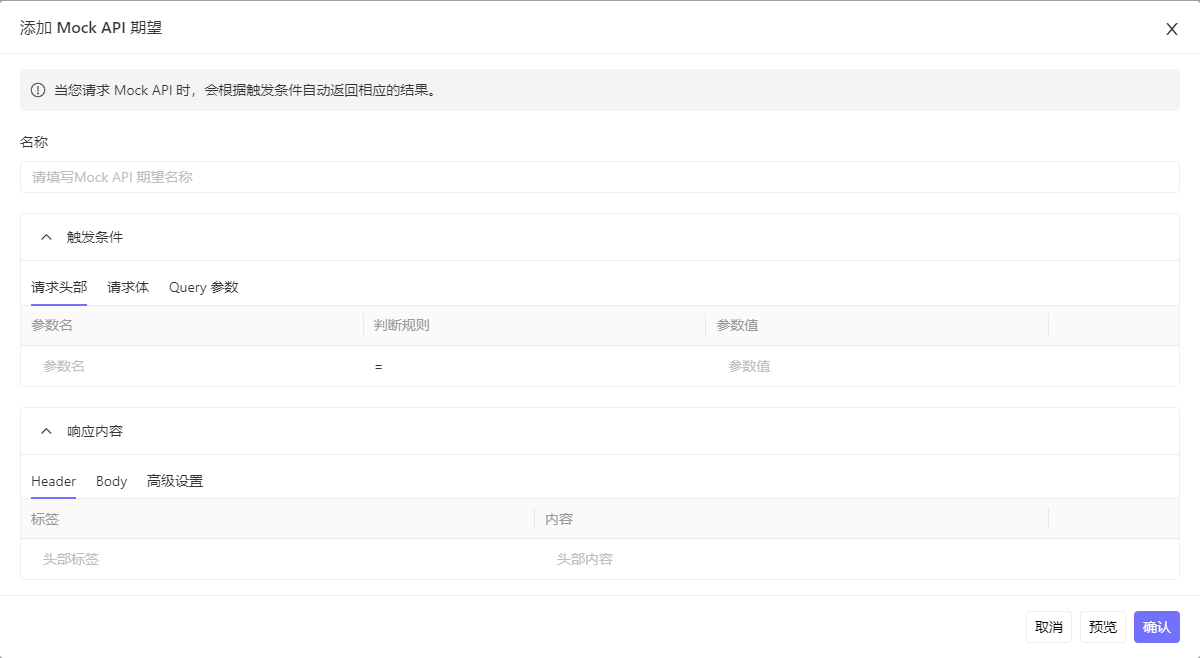
【接口测试工具】Eolink Apikit 快速入门教程
Eolink Apikit 下载安装【官方版】:https://www.eolink.com/apikit 发起 API 测试 进入 API 文档详情页,点击上方 测试 标签,进入 API 测试页,系统会根据 API 文档自动生成测试界面并且填充测试数据。 填写请求参数 首先填写好请…...

使用Python和OpenCV实现实时人脸检测并保存截图
在本篇博客中,我们将使用Python和OpenCV库实现一个实时人脸检测的小项目。我们将利用OpenCV中的Haar级联分类器来检测摄像头捕获的图像中的人脸。 项目功能 通过摄像头实时捕获视频流。使用Haar级联分类器检测视频帧中的人脸。在检测到的人脸周围绘制矩形框。实时…...

[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过
文章目录背景前情回顾描述方法约定MEMCG总览省流总结简介slub 相关 memcg机制kernel 5.9 版本之前结构体初始化具体实现kernel 5.9-5.14kernel 5.14 之后突破slab限制方法cross cache attackpage 堆风水总结背景 前情回顾 关于slab几个结构体的关系和初始化和内存分配和释放的…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
