二叉搜索树和AVL树

目录
一、二叉搜索树
1.什么是二叉搜索树
2.二叉搜索树的实现
(1)构建类
(2)查找函数
(3)插入函数
(4)删除函数
(5)补齐默认成员函数
(6)中序遍历函数
二、AVL树
1.什么是AVL树
2.AVL树的简易实现
(1)构建类
(2)插入函数实现准备
(3)AVL树的检验
一、二叉搜索树
1.什么是二叉搜索树
二叉搜索树(Binary Search Tree)是一种特殊的二叉树,它必须满足以下性质:
- 若左子树不为空,左子树中所有节点的键值都小于根节点的值。
- 若右子树不为空,右子树中所有节点的键值都大于根节点的值。
- 左右子树也分别为二叉搜索树。
- 空树也是搜索二叉树
简单地说,就是这个二叉树的任意一棵子树,它的左子树根节点值小于它的根节点值,它的右子树根节点值大于它的根节点值,这样的特性使得二叉搜索树的中序遍历结果是一个升序序列。这个特性使得二叉搜索树在搜索、插入和删除操作时具有高效性能,同时后面的AVL树和红黑树等许多数据结构也是基于它而实现。
2.二叉搜索树的实现
(1)构建类
依旧换汤不换药,在Binary Search Tree.h头文件中定义类,在test.cpp中写测试代码。
构建好下面的两个类,一个类是二叉树的节点类,另一个是二叉搜索树的这个类,在编写过程中注意包含需要的头文件。
#include<assert.h>
namespace my_BST
{template<class K>struct BSTreeNode{K _key;struct BSTreeNode* _left;struct BSTreeNode* _right;BSTreeNode(const K& x):_key(x), _left(nullptr), _right(nullptr){}};template<class K>class BSTree{typedef BSTreeNode<K> node;public://成员函数private:node* _root;//搜索二叉树的根节点};
}(2)查找函数
在一各二叉搜索树中查找数据很简单的,给定一个确定的值,先和该棵树的根进行比较,如果这个值小于根节点保存的值,那么就需要到它的左子树去寻找,如果这个值大于根节点,那么就需要到右子树去寻找。之后,再在新的子树中进行比较直到找到该值或者找到空位置,前者表示能找到,后者就表示找不到了。
bool find(const K& key)
{node* cur = _root;while (cur){if (key < cur->_key)//小于根左走{cur = cur->_left;}else if (key > cur->_key)//大于根右走{cur = cur->_right;}else{return true;//相等返回真}}return false;//找到空位置,肯定就不存在这个值
}还有另一种递归写法:
bool findR(const K& key, node* root)
{if(root == nullptr)return false; if(key < root->_key)findR(root->_left);else if(key > root->_key)findR(root->_right);elsereturn true;
}但是如果我们直接将这个函数递归函数写到public的成员函数中,我们会发现一个巨大的问题:我们需要传递二叉树的_root指针,而这个指针是内部封装的内容,用户层看不到。那么我们就需要再使用一次封装,将上面的函数定义为_findR函数,在类公共成员函数中使用findR函数调用它即可。
template<class K>
class BSTree
{typedef BSTreeNode<K> node;
public:bool findR(const K& key){_findR(key, _root);}
private:bool _findR(const K& key, node* root){if (root == nullptr)return false;else if (key < root->_key)return _findR(key, root->_left);else if (key > root->_key)return _findR(key, root->_right);elsereturn true;}node* _root;
};后面的我就不再将两个函数写在类中了。
(3)插入函数
插入和查找非常相似,通过相同的查找策略,这次我们需要找到空节点,然后在空节点位置新建节点,找到同样的元素就不再插入了。
bool insert(const K& key)
{if (_root == nullptr)//空树就直接插入{_root = new node(key);return true;}node* parent = nullptr;node* cur = _root;while (cur){if (key < cur->_key)//小于根左走{parent = cur;cur = cur->_left;}else if (key > cur->_key)//大于根右走{parent = cur;cur = cur->_right;}else//找到了需要插入的值,搜索二叉树的元素是不能重复的,插入失败{return false;}}cur = new node(key);if (key < parent->_key)//key小于根做左节点{parent->_left = cur;}else//大于根做右节点{parent->_right = cur;}return true;
}插入函数同样也可以写成递归的函数
bool insertR(const K& key)
{return _insertR(key, _root);
}bool _insertR(const K& key, node* root)
{if (root == nullptr){root = new node(key);return true;}else if (key < root->_key)//小于根向左走{return _insertR(key, root->_left);}else if (key > root->_key)//大于根向右走{return _insertR(key, root->_right);}else//找到相同的元素{return false;}
}(4)删除函数
删除函数的实现比较复杂,主要分为三种情况:
- 要删除的节点只有右子节点或既没有左子节点也没有右子节点
如果是叶子节点或者只有右子节点的节点,就可以先将该节点的父节点与它的右子节点进行链接,使这个右节点成为父节点的右节点,然后将该节点删除。同时被删除的也可能是根节点,需要判断并特殊处理。
- 要删除的节点只有左子节点
如果节点只有左子节点,可以将该节点的左子节点与其父节点进行链接,使这个左节点成为父节点的右节点(由于二叉搜索树的特性,右子树的内容都会比根大,所以右子树的左子树也可以做根的右子树),然后将该节点删除。同时被删除的也可能是根节点,需要判断并特殊处理。
- 要删除的节点有左、右子节点
此时需要寻找该节点右子树的最小值,将这个最小节点的值覆盖该节点,然后需要被被删除的节点就转化为了右子树的最左节点(右子树一直向左走直到没有左节点就是最小节点,此时满足情况一的删除条件)此时就可以使用原先的代码了,但此时不需要特殊处理了,因为被删除的节点一定不是根节点。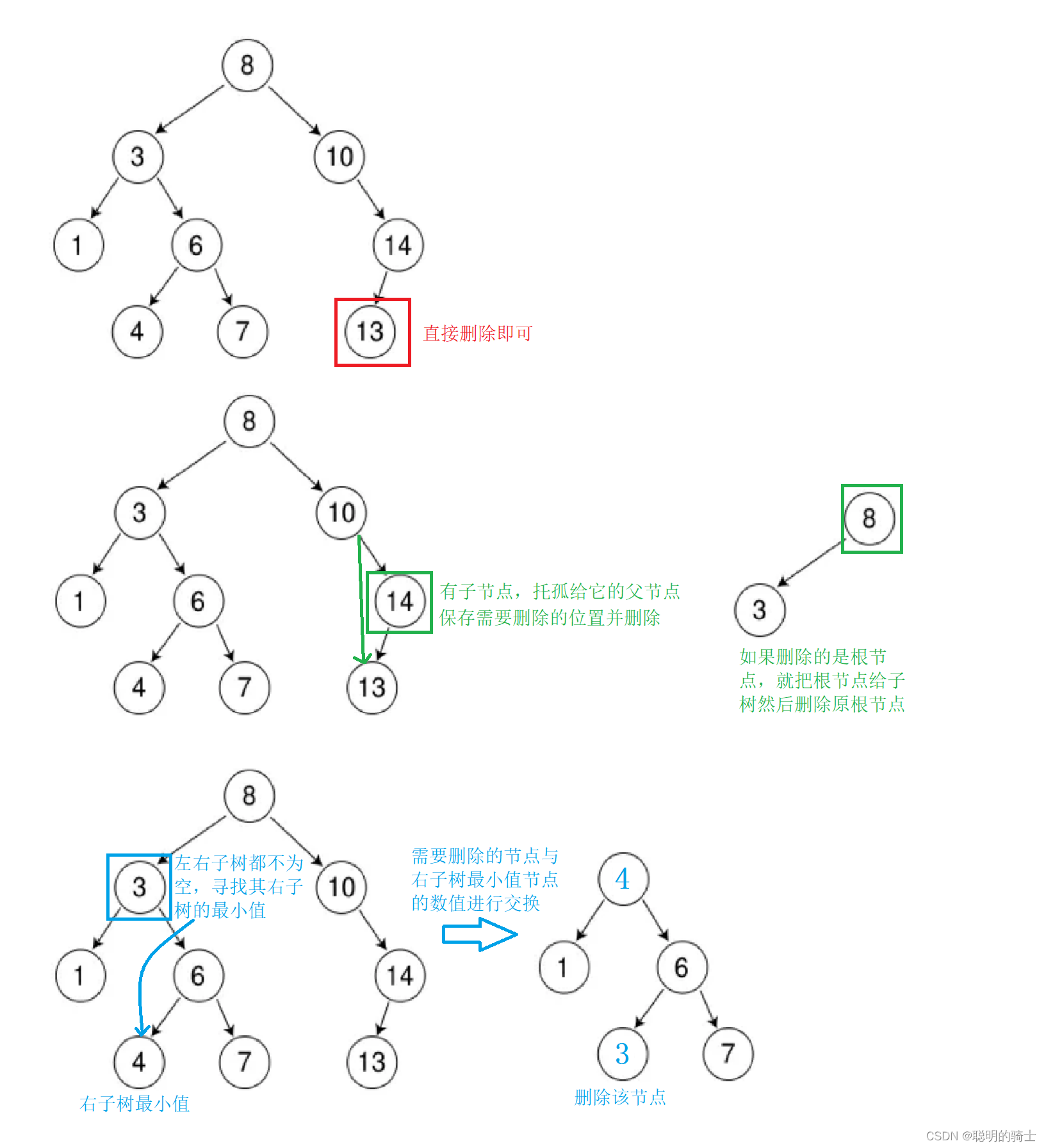
bool Erase(const K& key)
{//一共分为三种情况://要删除的节点只有右子节点或既没有左子节点也没有右子节点//要删除的节点只有左子节点//要删除的节点有左、右子节点//空树不能删除assert(_root != nullptr);//找寻该节点node* parent = nullptr;node* cur = _root;while (cur){if (key < cur->_key)//小于根左走{parent = cur;cur = cur->_left;}else if (key > cur->_key)//大于根右走{parent = cur;cur = cur->_right;}else{//找到了该节点//节点只有右子结点或既没有左子节点也没有右子节点if (cur->_left == nullptr){//根节点删除if (cur == _root)//或if(parent == nullptr){_root = _root->_right;}//非根节点删除else{if (parent->_left == cur){parent->_left = cur->_right;}else if (parent->_right == cur){parent->_right = cur->_right;}}delete cur;}//节点只有左子节点else if (cur->_right == nullptr){//根节点删除if (cur == _root)//或if(parent == nullptr){_root = _root->_right;}//非根节点删除else{if (parent->_left == cur){parent->_left = cur->_left;}else if (parent->_right == cur){parent->_right = cur->_left;}}delete cur;}//节点左、右子节点都有else{//找右子树的最小节点node* parent = cur;node* min_right = cur->_right;while (min_right->_left){parent = min_right;min_right = min_right->_left;}//覆盖cur->_key = min_right->_key;//托孤//由于min_right是右子树的最小节点,所以这个节点一定是一直向左走得到的//所以,当找到min_right时,它一定没有左子树,所以只需要托孤自己的右子节点即可if (parent->_left == min_right){parent->_left = min_right->_right;}else if (parent->_right == min_right){parent->_right = min_right->_right;}delete min_right;}return true;}}
}删除函数也有递归写法
首先先通过递归找到需要删除的节点,这个节点同样分为上面的三种情况,也同样按照上面的方式删除。不过注意我们此时传递的是引用,这就代表它传递的不只是子节点的地址,它也是它父节点的左或右子节点的地址(取决于该节点为左节点还是右节点),直接将引用进行赋值就改变了父节点的指向。如果我们使用传值的方式传递对象, 此时改变的只是这个临时对象,而不会改变父节点的指向。
BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);return *this;
}~BSTree()
{Destroy(_root);_root = nullptr;
}node* Copy(node* root)
{if (root == nullptr) //空树直接返回return nullptr;node* copyNode = new node(root->_key); //拷贝根结点copyNode->_left = Copy(root->_left); //拷贝左子树copyNode->_right = Copy(root->_right); //拷贝右子树return copyNode; //返回拷贝的树
}void Destroy(node* root)
{if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root
}(5)补齐默认成员函数
包括赋值运算符重载、析构函数和拷贝构造函数,都很简单
BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);return *this;
}~BSTree()
{Destroy(_root);_root = nullptr;
}node* Copy(node* root)
{if (root == nullptr) //空树直接返回return nullptr;node* copyNode = new node(root->_key); //拷贝根结点copyNode->_left = Copy(root->_left); //拷贝左子树copyNode->_right = Copy(root->_right); //拷贝右子树return copyNode; //返回拷贝的树
}void Destroy(node* root)
{if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root
}(6)中序遍历函数
这个函数就很简单了,它的实现是用于检验二叉搜索树的中序遍历是否为升序。
void Inorder()
{_Inorder(_root);
}void _Inorder(const node* root)
{if (root == nullptr)return;_Inorder(root->_left);std::cout << root->_key << ' ';_Inorder(root->_right);
}二、AVL树
1.什么是AVL树
二叉搜索树是有其局限性的,它的查找数据的时间复杂度为O(N)。这里你可能会不理解,二叉搜索树每一层数据成倍数级上涨,如果有三层数据最多查找三次就够了。为什么不是O(logN)呢?
其实这种想法是没有问题的,但是我们不妨设想一下一些极端的情况,比如说我们按降序插入多个数字,那么这些数字都会插入到左树,就导致这个二叉搜索树一边十分地高,近似一个顺序排列的数组,这也是二叉搜索树最糟糕的状态,查找的时间复杂度就是O(N)。一个程序的时间复杂度应该是分析它耗时最长的情况,所以时间复杂度为O(N)。
此时AVL树就出场了,AVL树就是为了解决二叉搜索树两子树高度差别过大的问题而建立的。它可以通过旋转的方式在一侧子树过高时降低它,以尽可能达到二叉搜索树搜索数据的最佳状态。故,它的中文名称叫做平衡二叉搜索树。
2.AVL树的简易实现
(1)构建类
AVL树调节平衡有很多种方式,我们使用平衡因子法。
namespace MY_AVLTree
{template<class K, class V>struct AVLTreeNode{pair<K, V> _kv;//pair是一个由两个数据组成的结构体AVLTreeNode* _parent;//父指针AVLTreeNode* _left;//左子树指针AVLTreeNode* _right;//右子树指针int _bf; //平衡因子AVLTreeNode(pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}};template<class K, class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public://构造函数AVLTree():_root(nullptr){}private:Node* _root;};
}(2)插入函数实现准备
在AVL树的实现中,我们只学习插入函数。
它的实现主要包括三个部分:查找需要插入空位置 -> 更新平衡因子 -> 在平衡因子出现大于1或小于1的情况下对树进行旋转。
第一步:查找空位置
bool insert(pair<K, V>& kv)
{if (_root == nullptr)//树中还没有元素,直接插入即可{_root = new Node(kv);return true;}//定义一个parent指针和一个cur指针不断向下寻找可以插入的节点Node* parent = nullptr;Node* cur = _root;while (cur)//小于往左走,大于往右走{if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//此时的cur就是可以插入的空位置//…………//接下来的函数操作//…………
}第二步:更新平衡因子
平衡因子是调节树高的重要变量,每一个AVL树的节点都有一个平衡因子,它是该节点右子树高度减去左子树高度的值,表明了右树比左树高多少。
更新平衡因子是一个十分重要的过程,平衡因子的调节遵循以下条件:
- 新增节点在右子树,右子树高度加一,对应父节点平衡因子加一;新增在左子树,左子树高度加一,对应父节点平衡因子减一
- 新增后被插入节点的父节点平衡因子如果为0,则表明要么是右树不为空且节点插入到左树,要么是左树不为空且节点插入到右树。相当于插入一个节点补齐了子树中较矮的一侧,此时父节点的子树高度不变,也就不需要继续向上调节平衡因子
- 新增后被插入节点的父节点平衡因子如果为1或-1,则表明本来平衡的树在一侧又插入了一个节点,这次父节点子树的高度就被改变了,需要继续向上调整平衡因子
- 当平衡因子大于等于2或者小于等于-2时,此时该节点的左树和右树的高度差2,此时需要旋转才可以降低较高的子树高度
bool insert(pair<K, V>& kv)
{if (_root == nullptr)//树中还没有元素,直接插入即可{_root = new Node(kv);return true;}//定义一个parent指针和一个cur指针不断向下寻找可以插入的节点Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了空位置cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;//插入数据cur->_parent = parent;//把新插入元素的父节点与其链接起来}else{parent->_right = cur;//插入数据cur->_parent = parent;//把新插入元素的父节点与其链接起来}//更新平衡因子while (parent){//新增的节点在左子树还是右子树if (parent->_right == cur){//新增在右子树,右子树高度加一,对应父节点平衡因子加一++parent->_bf;}else if (parent->_left == cur){//新增在左子树,左子树高度加一,对应父节点平衡因子减一--parent->_bf;}//更新子树平衡因子,根据子树高度是否变化,判断是否需要继续向上更新平衡因子和旋转当前树//1.parent->_bf == 0说明之前parent->_bf一定是 1 或者 -1//说明之前parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新//2.parent->_bf == 1 或 -1 说明之前是parent->_bf == 0,两边一样高,现在插入一边更高了,//parent所在子树高度变了,继续往上更新//3.parent->_bf == 2 或 -2,说明之前parent->_bf == 1 或者 -1,现在插入严重不平衡,违反规则//就地处理--旋转if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转子树if (parent->_bf == 2 && cur->_bf == 1)//右树高{RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1)//左树高{RotateR(parent);//右单旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);//左右双旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);//右左双旋}else{assert(false);}break;}else{assert(false);}}
}第三步:四种旋转
- 左单旋
左单旋主要用于下面的情况:右侧高且从需要被旋转的树根节点开始有连续的三个右节点
对于下面的情况就是将较高的3节点转移到6节点的左子节点然后将b子树变为3节点的右子树,最后调节平衡因子
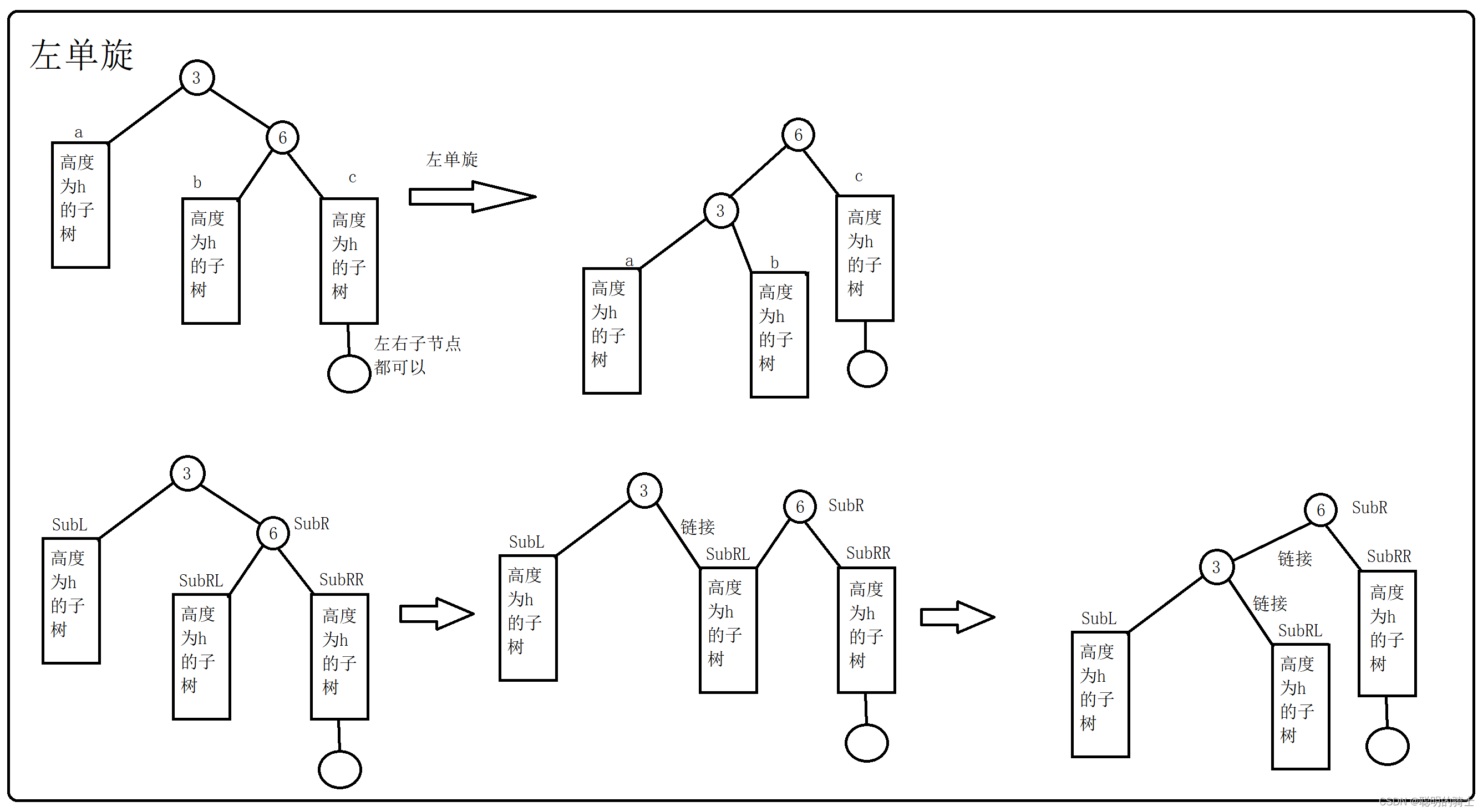
代码实现:
//左单旋
void RotateL(Node* parent)
{Node* SubR = parent->_right;//必不为空Node* SubRL = SubR->_left;//可能为空Node* ppnode = parent->_parent;//保存根的父节点parent->_right = SubRL;if (SubRL)SubRL->_parent = parent;SubR->_left = parent;parent->_parent = SubR;if (ppnode == nullptr){_root = SubR;SubR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = SubR;}else{ppnode->_right = SubR;}}SubR->_bf = 0;parent->_bf = 0;
}- 右单旋
右单旋主要用于下面的情况:左侧高且从需要被旋转的树根节点开始有连续的三个左节点
对于下面的情况就是将较高的3节点转移到1节点的右子节点然后将b子树变为3节点的左子树,最后调节平衡因子
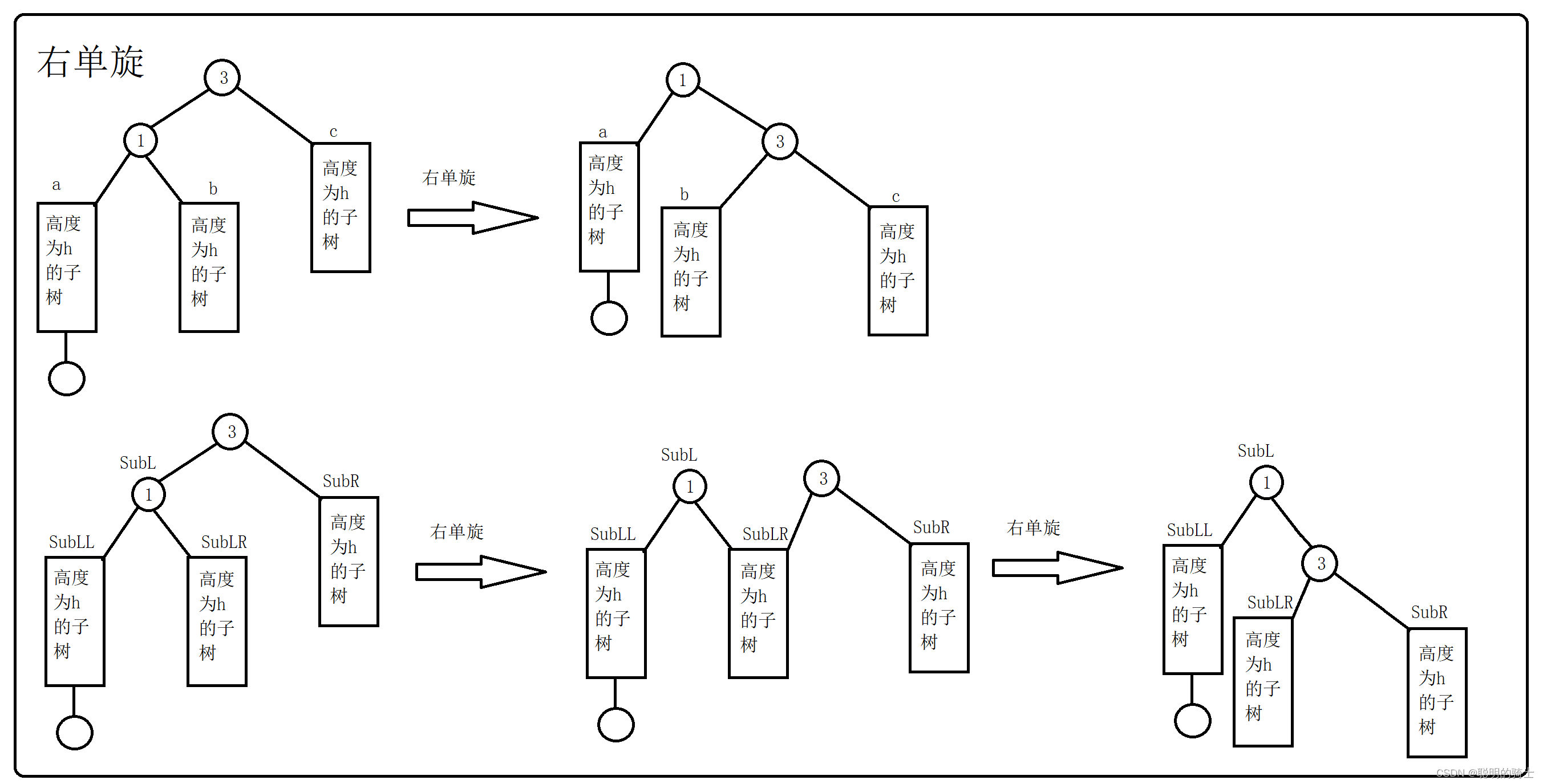
代码实现:
//右单旋
void RotateR(Node* parent)
{Node* SubL = parent->_left;Node* SubLR = SubL->_right;Node* ppnode = parent->_parent;parent->_left = SubLR;if (SubLR)SubLR->_parent = parent;SubL->_right = parent;parent->_parent = SubL;if (ppnode == nullptr){SubL->_parent = nullptr;_root = SubL;}else{if (ppnode->_left == SubL){ppnode->_left = SubL;}else{ppnode->_right = SubL;}}SubL->_bf = 0;parent->_bf = 0;
}- 左右双旋
左右双旋主要用于下面的情况:从需要被旋转的树根节点的子节点开始存在一个左子节点,再在这个左子节点接上右子节点
对于下面的情况就是以1为根节点进行左单旋,然后就会转化为右单旋的情况,再对以3为根做右单旋,最后根据下面的三种情况调整平衡因子
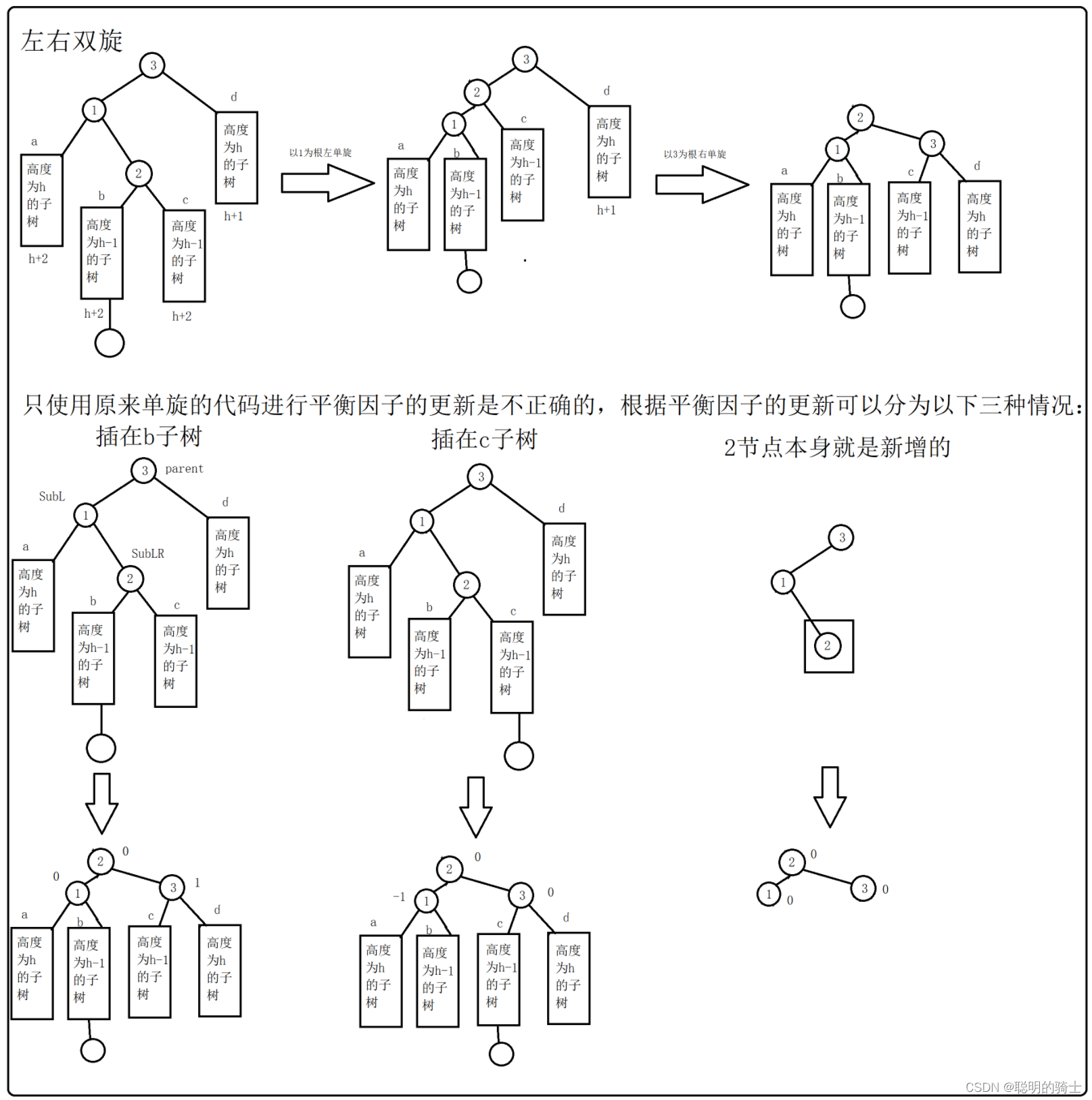
代码实现:
//左右双旋
void RotateLR(Node* parent)
{Node* SubL = parent->_left;Node* SubLR = SubL->_right;int bf = SubLR->_bf;RotateL(parent->_left);RotateR(parent);//插在b子树if (bf == -1){parent->_bf = 1;SubL->_bf = 0;SubLR->_bf = 0;}//插在c子树else if (bf == 1){parent->_bf = 0;SubL->_bf = -1;SubLR->_bf = 0;}//本身是新增else if (bf == 0){parent->_bf = 0;SubL->_bf = 0;SubLR->_bf = 0;}//错误情况else{assert(false);}
}- 右左双旋
右左双旋主要用于下面的情况:从需要被旋转的树根节点的子节点开始存在一个右子节点,再在这个右子节点接上左子节点
对于下面的情况就是以4为根节点的树进行右单旋,然后就会转化为左单旋的情况,再对以2为根的树做左单旋,最后根据下面的三种情况调整平衡因子
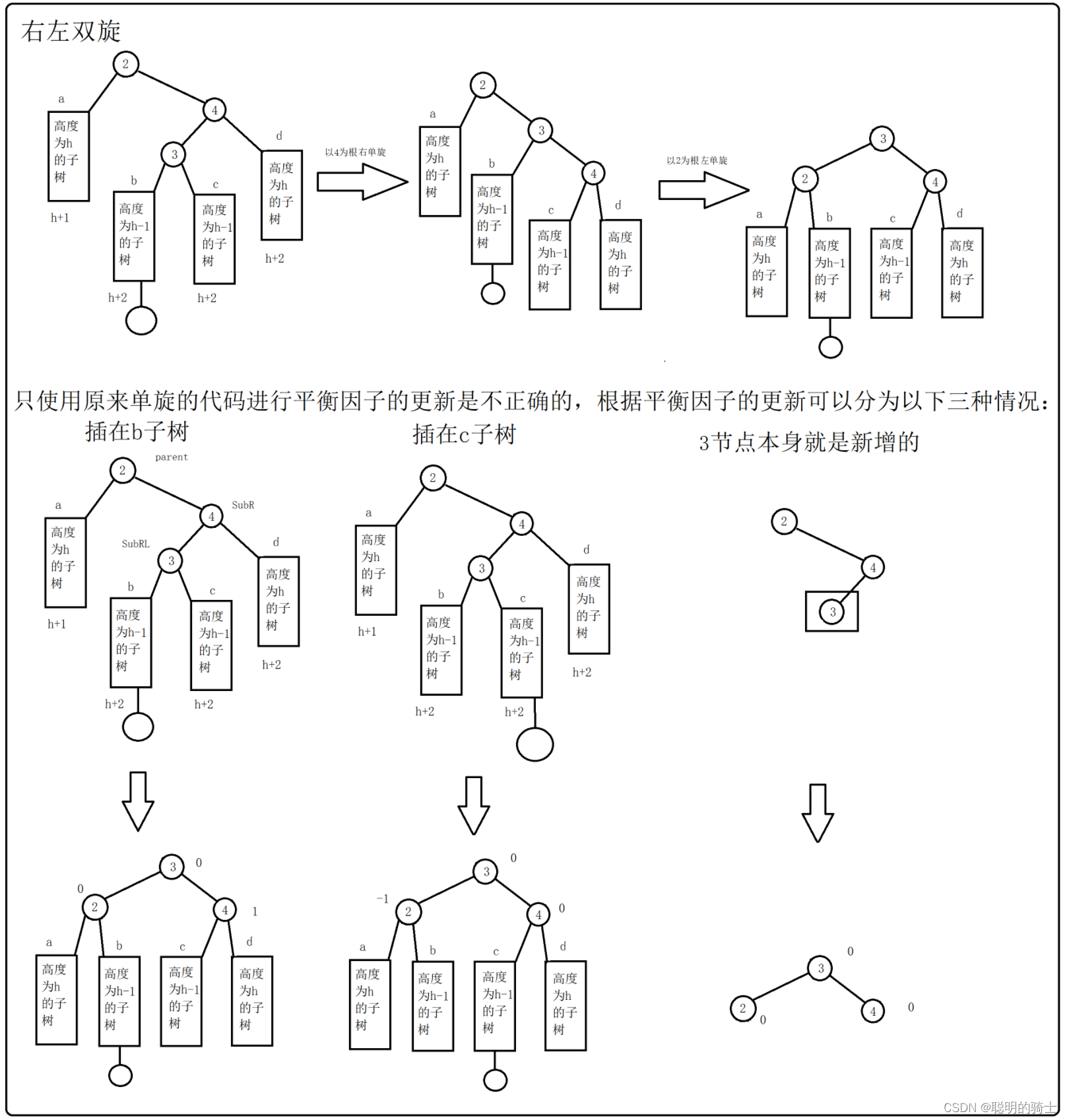
代码实现:
//右左双旋
void RotateRL(Node* parent)
{Node* SubR = parent->_right;Node* SubRL = SubR->_left;int bf = SubRL->_bf;RotateR(parent->_right);RotateL(parent);//插在b子树if (bf == -1){parent->_bf = 0;SubR->_bf = 1;SubRL->_bf = 0;}//插在c子树else if (bf == 1){parent->_bf = -1;SubR->_bf = 0;SubRL->_bf = 0;}//本身是新增else if (bf == 0){parent->_bf = 0;SubR->_bf = 0;SubRL->_bf = 0;}//错误情况else{assert(false);}
}(3)AVL树的检验
AVL树的检验
bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr){return true;//空树一定是AVL树}int leftHeight = Height(root->_left);//计算左树的高度int rightHeight = Height(root->_right);//计算右树的高度if (rightHeight - leftHeight != root->_bf)//平衡因子必须满足右树高减左树高{cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2//左树和右树的高度差绝对值不超过1&& IsBalance(root->_left)&& IsBalance(root->_right);
}相关文章:

二叉搜索树和AVL树
目录 一、二叉搜索树 1.什么是二叉搜索树 2.二叉搜索树的实现 (1)构建类 (2)查找函数 (3)插入函数 (4)删除函数 (5)补齐默认成员函数 (6…...
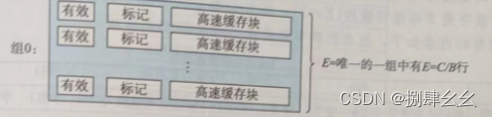
计算机体系结构量化研究方法【2】高速缓存Cache
目录1.计算机存储层次结构2.缓存相关概念3.缓存组织方式4.Cache回写机制5.Cache性能量化1.计算机存储层次结构 计算机存储层次结构可以看作是一个金字塔,越靠上层,容量越小,速度越快 L0:寄存器----CPU的寄存器保存着Cache取出的…...

初识设计模式 - 迭代器模式
简介 迭代器设计模式(Iterator Design Pattern),也叫作游标设计模式(Cursor Design Pattern)。 迭代器模式将集合对象的遍历操作从集合类中拆分出来,放到迭代器类中,让两者的职责更加单一。 …...

三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录 一.前言 二. 三路快排 😍算法思想: 😍算法实现步骤: 😍三指针单趟排序的实现: 😍非递归快排完全体: 🤔与C标准库里的快排进行对比测试: 三.快排时间复杂度再分析 一.前言 http://t.csdn.cn/mz8dghttp://…...

Eyeshot Ultimate 2023 Crack
Eyeshot Ultimate 2023 Crack 已经引入了文档类。 工作区。文档现在包含绘制场景内容所需的所有数据。 2022版GEntities已被删除。 最后,一个真正的跨平台中立核心产品是可用的。 新功能 曲线、平面、曲面和体积网格。 屏幕空间环境光遮挡。 托管ReadDWG和ReadDXF类…...
JAVA-8-[SpringBoot]入门程序案例和原理分析
Spring Boot框架入门教程(快速学习版) Spring Boot教程BooTWiki.COM 1 Spring Boot Spring Boot是Pivotal(关键性的)团队在Spring的基础上提供的一套全新的开源框架,其目的是为了简化Spring应用的搭建和开发过程。Spring Boot去除了大量的X…...

前端工程化
一、AST (抽象语法树,Abstract Syntax Tree) 手把手带你走进Babel的编译世界 - 掘金 (juejin.cn) 1、概念 我们所写的代码转换为机器能识别的一种树形结构,本身是由一堆节点(Node)组成,每个节…...
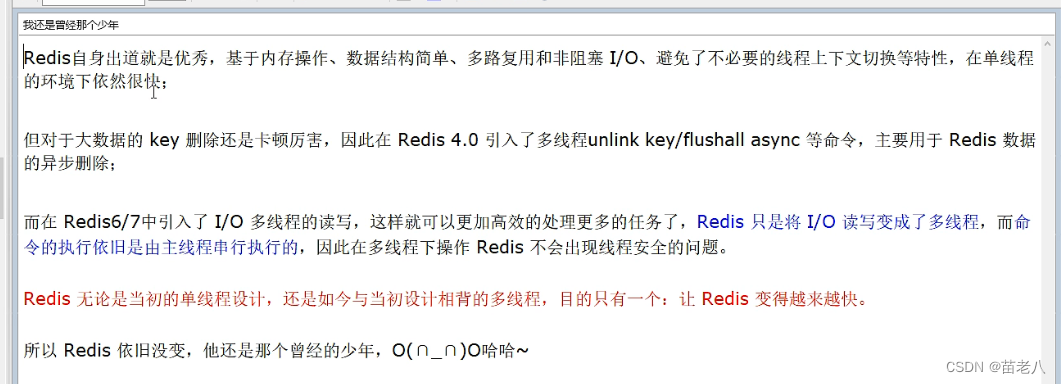
【redis】单线程 VS 多线程(入门)
【redis】单线程 VS 多线程(入门) 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成&#…...

2023蓝桥杯Java研究生组赛题
蓝桥杯Java研究生组、JavaA组看过来,这两个组别题目基本一样 第一次参加了Java研究生组,Java组应该没有C/C那么卷吧,主要是觉得Java组可以避开很多ACM大佬,前面几题感觉难度还行没有特别难,后面几个大题依旧是没法做&a…...

多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测
多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测 目录多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测,CNN-BiLSTM-Atte…...
)
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…...
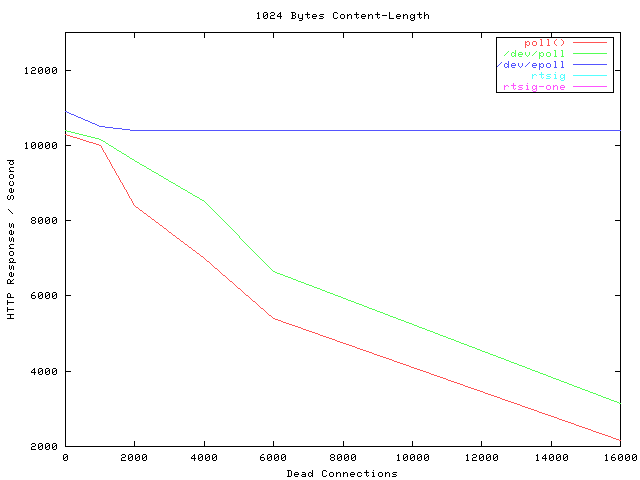
linux内核之select/poll/epoll
一些主流应用IO多路复用技术,突破高并发问题,如nginx、redis、netty,分布式服务框架dubbo,大数据组件hadoop、spark、flink、hbase纷纷使用netty作为网络通信组件。 一、背景:C10K问题 The C10K problem 最早被Dan …...

文件流下载
文件下载 后端传给前端json数据流,前端拿到之后存放在自定义的文件中import axios from "axios"; import qs from "query-string"; import {Notification } from "@arco-design/web-vue"; // 接口中需要含有文件名fileName export function dow…...

C语言模拟实现:atoi函数
在实现atoi之前我们先来了解一下atoi函数的作用是什么: 目录 1.实例演示 2.模拟实现 2.1 判断是否为空指针 2.2判断是否为空字符串 2.3判断正负号 2.4判断非数字字符 2.5判断是否越界 2.6完整代码 1.实例演示 //实例演示 #include <stdio.h> #include …...
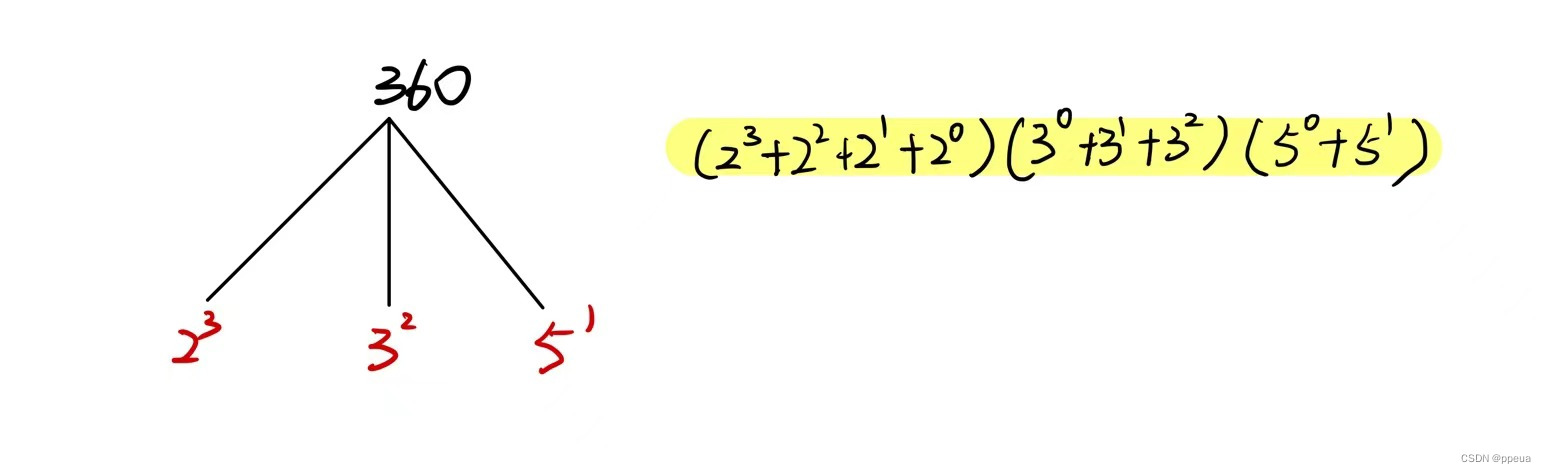
LeetCode.每日一题 2427. 公因子的数目
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
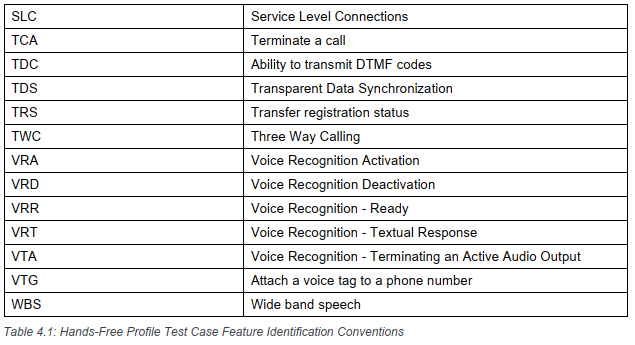
蓝牙BQB认证 - HFP profile配置说明
零.声明 本专栏文章我们会以连载的方式持续更新,本专栏计划更新内容如下: 第一篇:蓝牙综合介绍 ,主要介绍蓝牙的一些概念,产生背景,发展轨迹,市面蓝牙介绍,以及蓝牙开发板介绍。 第二篇:Trans…...
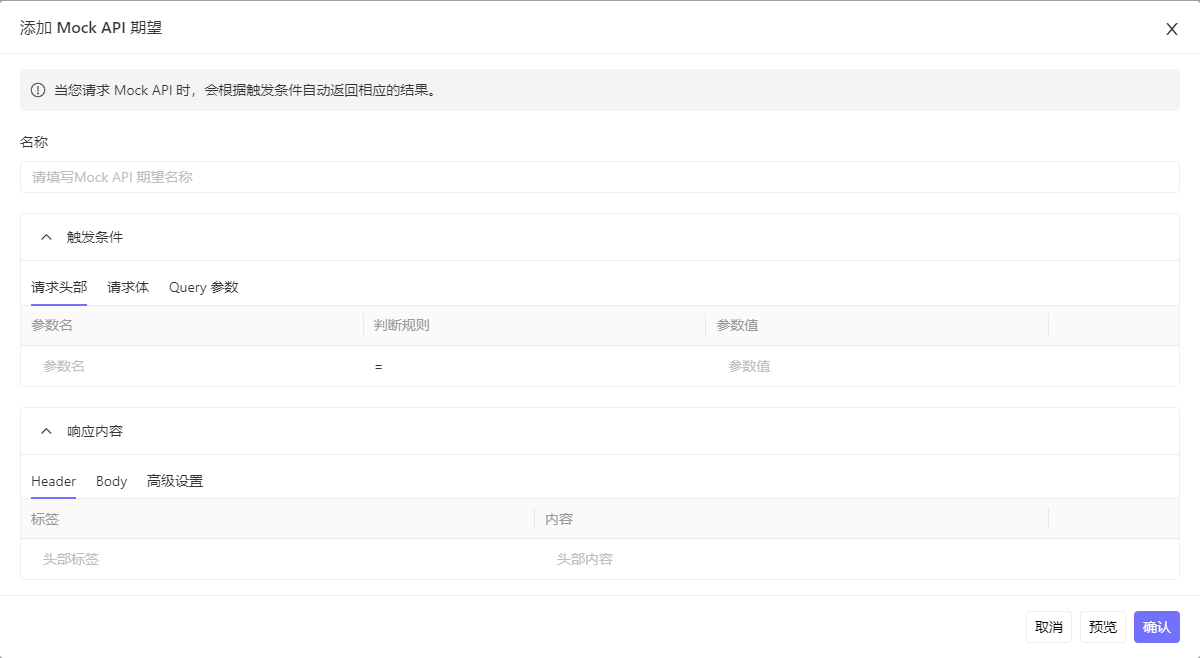
【接口测试工具】Eolink Apikit 快速入门教程
Eolink Apikit 下载安装【官方版】:https://www.eolink.com/apikit 发起 API 测试 进入 API 文档详情页,点击上方 测试 标签,进入 API 测试页,系统会根据 API 文档自动生成测试界面并且填充测试数据。 填写请求参数 首先填写好请…...

使用Python和OpenCV实现实时人脸检测并保存截图
在本篇博客中,我们将使用Python和OpenCV库实现一个实时人脸检测的小项目。我们将利用OpenCV中的Haar级联分类器来检测摄像头捕获的图像中的人脸。 项目功能 通过摄像头实时捕获视频流。使用Haar级联分类器检测视频帧中的人脸。在检测到的人脸周围绘制矩形框。实时…...

[linux kernel]slub内存管理分析(7) MEMCG的影响与绕过
文章目录背景前情回顾描述方法约定MEMCG总览省流总结简介slub 相关 memcg机制kernel 5.9 版本之前结构体初始化具体实现kernel 5.9-5.14kernel 5.14 之后突破slab限制方法cross cache attackpage 堆风水总结背景 前情回顾 关于slab几个结构体的关系和初始化和内存分配和释放的…...
)
MySQL创建数据库(CREATE DATABASE语句)
在 MySQL 中,可以使用 CREATE DATABASE 语句创建数据库,语法格式如下: CREATE DATABASE [IF NOT EXISTS] <数据库名> [[DEFAULT] CHARACTER SET <字符集名>] [[DEFAULT] COLLATE <校对规则名>]; [ ]中的内容是可选的。语…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
