力扣:字符串中的第一个唯一字符(C++实现)


题目部分:
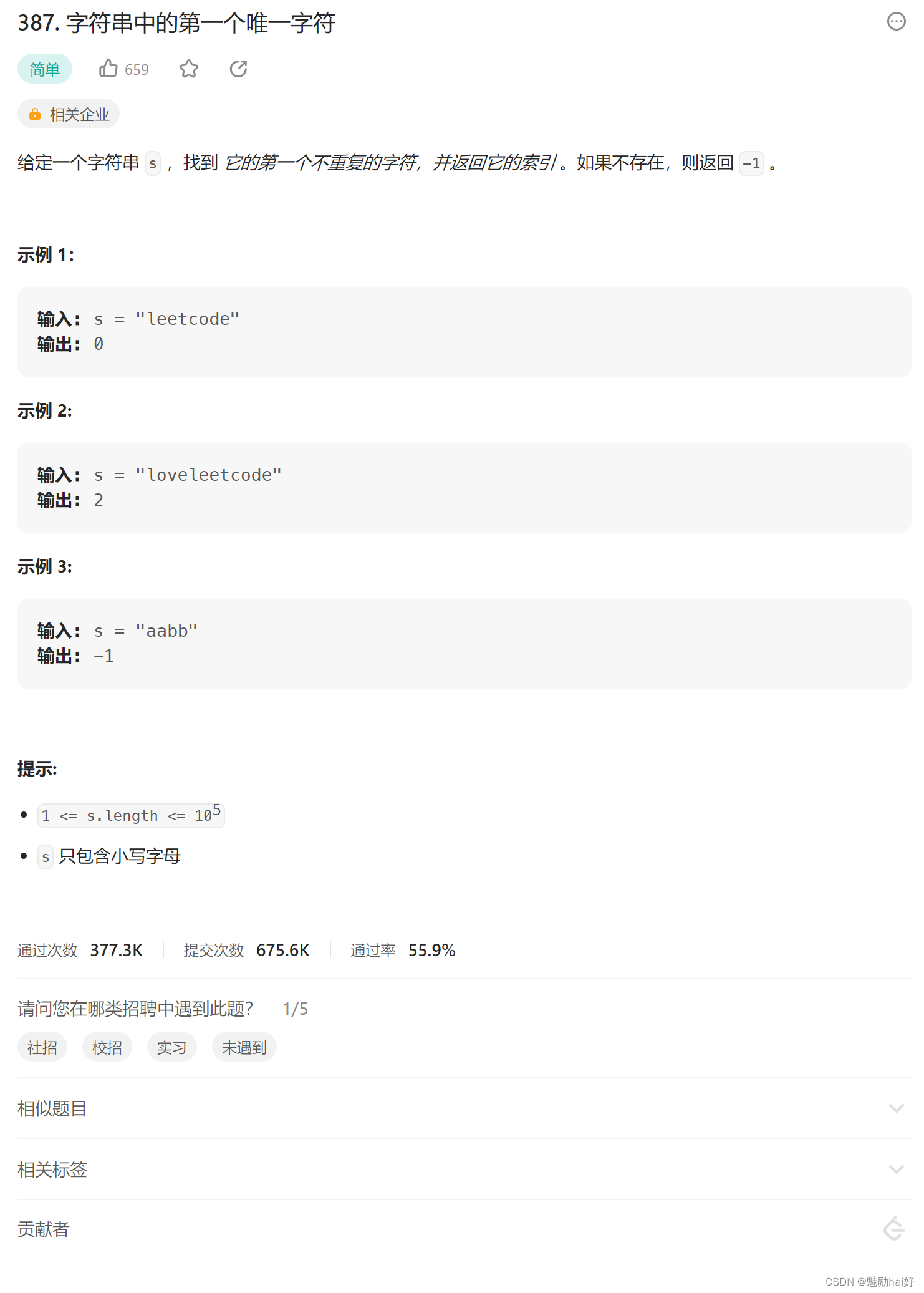
解题思路:
方案一:
首先认真审题的小伙伴们一定会发现就是题目给了提示只包含小写字母,也就是说我们的排查范围是小写的26个字母。为了怕有的友友们一时短路想不起来,我就其按照顺序列出来吧。
即:a、b、c、d、e、f、g、h、i、j、k、l、m、n、o、p、q、r、s、t、u、v、w、x、y、z
根据题意,我们的目标就是从给出的字符串中,找出出现的第一个不重复出现的小写26个字母中的一个,并将其对应在字符串数组中的下标位置返回去;若找完整个字符串后,均为重复出现的子母,即未发现只出现一次的子母,则返回-1。
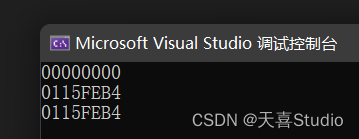
附:ASCII表
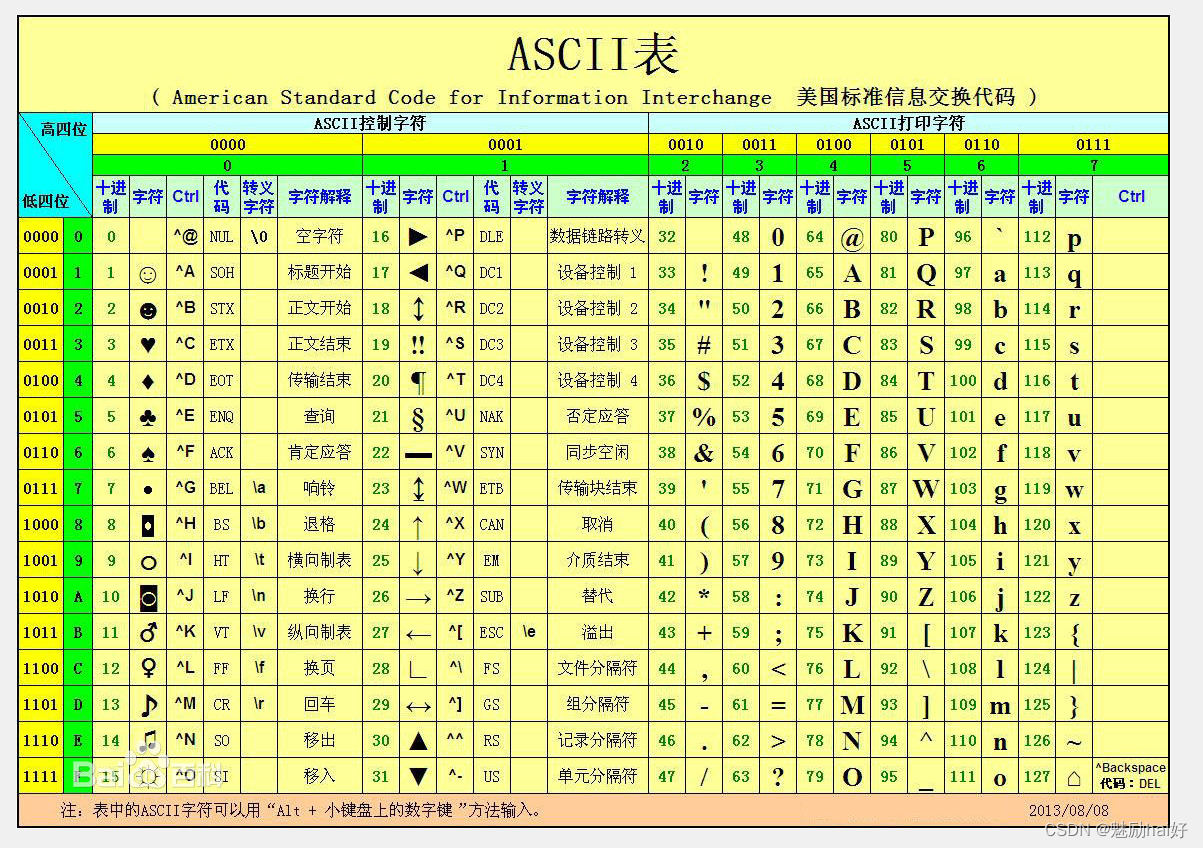
结合我们的ASCII表就可以很轻松的做出此题来,根据该表的提示,我们可以发现初始字母a所映射对应的整数是97,那么我们就可以开始做文章了。
定义一个计算每个小写字母出现次数的数组(默认我都是按照26个字母的顺序),并初始化为0。
紧接着用一个循环来统计出每个字母所出现的次数,循环内如何操作呢?代码走的逻辑就是拿当前字符串中当前对应的字母映射的整数值减去字母a映射的整数值,就能得知该字母在我们统计出现次数数组中的位置,并表示它已经出现一次了,所以要在原有次数上加一。
为了怕大家不懂我统计次数循环内代码走的逻辑,我特意拿示例1来做示范讲解。
示例1给的字符串第一个字母是l,在ASCII表映射对应的整数是108,前面我们不是有讲到初始字母a在该表映射对应的整数是97吗?用108-97=11,也就是代表数组中的第11个位置(也就是l的位置)的字母出现了一次【需要清楚的是数组下标是从0开始,家人们别忘记了】,因此要在该元素位置次数+1。

很多xdm可能会疑惑为什么要减字母a呢?干嘛不减字母b呢?这就是可能you钻牛角尖了。我在前面就有说过我默认的字母数组出现次数的排序,是按照它们原本的顺序。对应关系就是我下图所示:

只有从减字母a开始才能对应的了上图的关系,若到这里还不能理解的话,我建议大神你回炉重造!

前面所的是第一个循环,接着是代码中出现的第二个循环的作用——就是找出这个字符串中第一个不重复的字符,然后将其数组的下标返回回去。这第二个循环是需要基于第一个循环的,若字母都是至少出现了两次(即重复),就意味着并不符合题意的要求,按照题目的规定就返回-1回去。
如果你理解了前面第一个循环那么第二个循环理解就会相对简单,走的逻辑跟第一个循环类似,只不过是为了找出只出现1次的字母,顺带将其数组下标返回即可完成题目要求。

方案一演示代码讲解如下:

附:方案一代码提取:
class Solution {
public:int firstUniqChar(string s) {// 定义26个字母出现次数的数组,初始化都为0// 默认的26个字母顺序为:a、b、c、d、e...x、y、zint countArray[26] = { 0 };// 统计每个字母所出现的次数for (size_t i = 0; i < s.size(); ++i){countArray[s[i] - 'a']++;}// 找出它第一个不重复的字符,并返回数组下标for (int j = 0; j < s.size(); ++j){if (countArray[s[j] - 'a'] == 1){return j;}}return -1;}
};
测试结果:
方案一:
不出意外的话家人们必定是狠狠拿下!

备注:
楼主不才,不喜勿喷,若有错误或需要改进的地方,非常感谢你的指出,我会积极学习采纳。谢谢家人们一直以来的支持和鼓励,我会继续努力再接再励创作出更多优质的文章来回报家人们的。编程爱好的xdm,若有编程学习方面的问题可以私信我一同探讨(我尽力帮),毕竟“众人拾柴火焰高”,大家一起交流学习,共同进步!

2023年4月8日
相关文章:

力扣:字符串中的第一个唯一字符(C++实现)
题目部分: 解题思路: 方案一: 首先认真审题的小伙伴们一定会发现就是题目给了提示只包含小写字母,也就是说我们的排查范围是小写的26个字母。为了怕有的友友们一时短路想不起来,我就其按照顺序列出来吧。 即&#x…...

攻防世界 favorite_number mfw、[BJDCTF2020]ZJCTF,不过如此
favorite_number 进入环境得到源码 <?php //php5.5.9 $stuff $_POST["stuff"]; $array [admin, user]; if($stuff $array && $stuff[0] ! admin) {$num $_POST["num"];if (preg_match("/^\d$/im",$num)){if (!preg_match("…...

SummingMergeTree
假设有这样⼀种查询需求:终端⽤户只需要查询数据的汇总结果,不关⼼明细数据,并且数据的汇总条件是预先明确的(GROUP BY 条件明确,且不会随意改变)。 对于这样的查询场景,在ClickHouse中如何解决…...

JUC并发编程基础篇第一章之进程/并发/异步的概念[理解基本概念]
1. 进程和线程的概念 进程: 系统正在运行的一个应用程序;程序一旦运行就是一个进程;进程是资源分配的最小单位 线程: 是进程的实际运行单位;一个人进程可以并发控制多个线程,每条线程并行执行不同的任务 区别: 进程基本上相互独立的;而线程存在于进程内,是进程…...
c语言—指针进阶
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...

总结二分法
杨辉三角形(快速查找唯一值,mid型) //二分法解//流程:最大列->起点行->2k--n之间究竟哪一行(二分排列组合)->找到行数就等差数列对应位置#include<stdio.h> #include<stdlib.h>//注意排列组合的规律是建立在…...
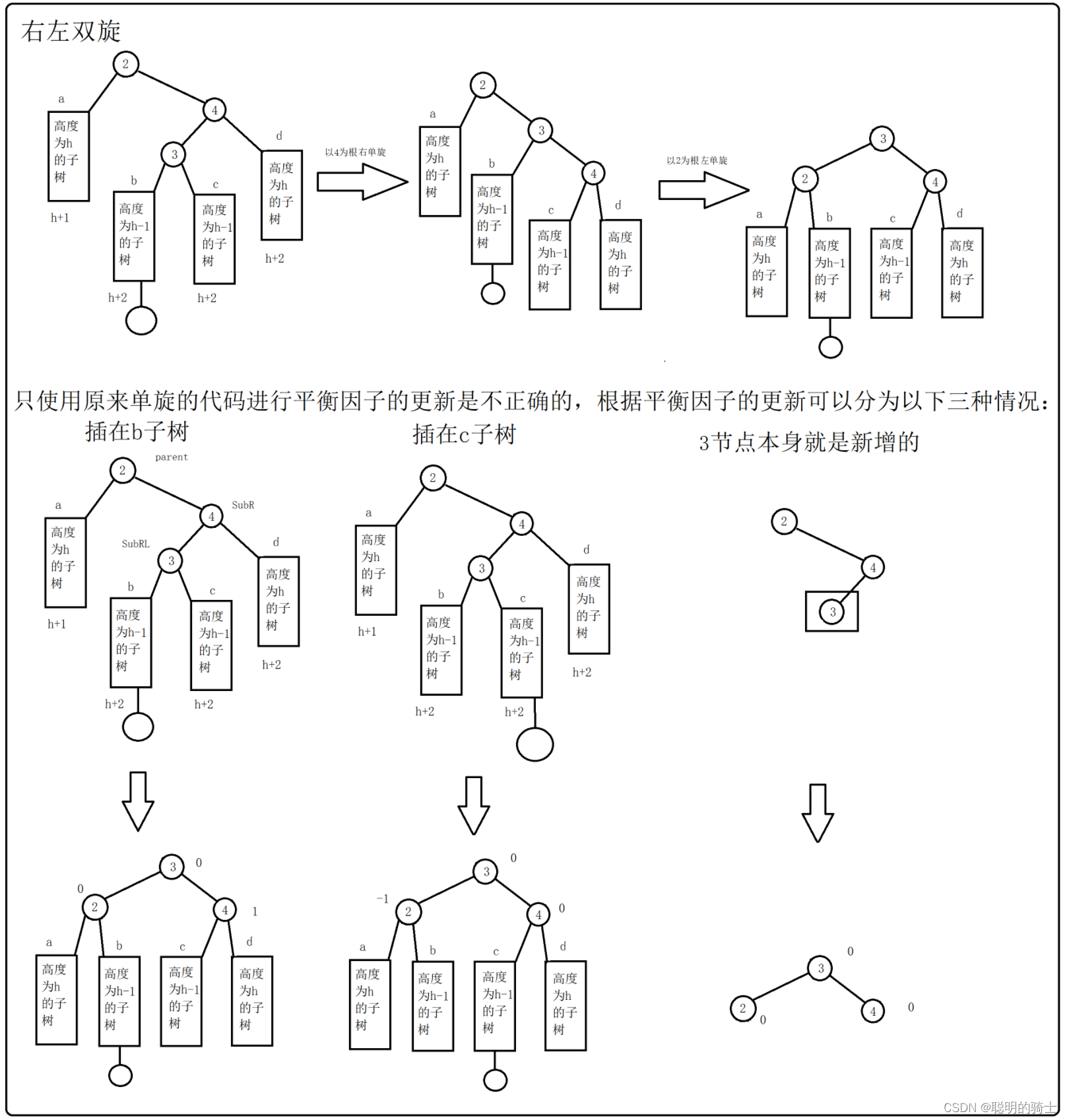
二叉搜索树和AVL树
目录 一、二叉搜索树 1.什么是二叉搜索树 2.二叉搜索树的实现 (1)构建类 (2)查找函数 (3)插入函数 (4)删除函数 (5)补齐默认成员函数 (6…...
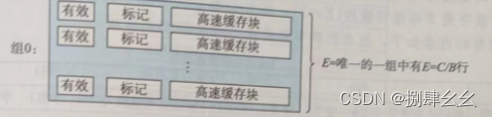
计算机体系结构量化研究方法【2】高速缓存Cache
目录1.计算机存储层次结构2.缓存相关概念3.缓存组织方式4.Cache回写机制5.Cache性能量化1.计算机存储层次结构 计算机存储层次结构可以看作是一个金字塔,越靠上层,容量越小,速度越快 L0:寄存器----CPU的寄存器保存着Cache取出的…...

初识设计模式 - 迭代器模式
简介 迭代器设计模式(Iterator Design Pattern),也叫作游标设计模式(Cursor Design Pattern)。 迭代器模式将集合对象的遍历操作从集合类中拆分出来,放到迭代器类中,让两者的职责更加单一。 …...

三路快排(基于三指针单趟排序的快速排序)+快排时间复杂度再分析
目录 一.前言 二. 三路快排 😍算法思想: 😍算法实现步骤: 😍三指针单趟排序的实现: 😍非递归快排完全体: 🤔与C标准库里的快排进行对比测试: 三.快排时间复杂度再分析 一.前言 http://t.csdn.cn/mz8dghttp://…...

Eyeshot Ultimate 2023 Crack
Eyeshot Ultimate 2023 Crack 已经引入了文档类。 工作区。文档现在包含绘制场景内容所需的所有数据。 2022版GEntities已被删除。 最后,一个真正的跨平台中立核心产品是可用的。 新功能 曲线、平面、曲面和体积网格。 屏幕空间环境光遮挡。 托管ReadDWG和ReadDXF类…...
JAVA-8-[SpringBoot]入门程序案例和原理分析
Spring Boot框架入门教程(快速学习版) Spring Boot教程BooTWiki.COM 1 Spring Boot Spring Boot是Pivotal(关键性的)团队在Spring的基础上提供的一套全新的开源框架,其目的是为了简化Spring应用的搭建和开发过程。Spring Boot去除了大量的X…...

前端工程化
一、AST (抽象语法树,Abstract Syntax Tree) 手把手带你走进Babel的编译世界 - 掘金 (juejin.cn) 1、概念 我们所写的代码转换为机器能识别的一种树形结构,本身是由一堆节点(Node)组成,每个节…...
【redis】单线程 VS 多线程(入门)
【redis】单线程 VS 多线程(入门) 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成&#…...

2023蓝桥杯Java研究生组赛题
蓝桥杯Java研究生组、JavaA组看过来,这两个组别题目基本一样 第一次参加了Java研究生组,Java组应该没有C/C那么卷吧,主要是觉得Java组可以避开很多ACM大佬,前面几题感觉难度还行没有特别难,后面几个大题依旧是没法做&a…...

多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测
多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测 目录多维时序 | MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 MATLAB实现CNN-BiLSTM-Attention多变量时间序列预测,CNN-BiLSTM-Atte…...
)
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…...
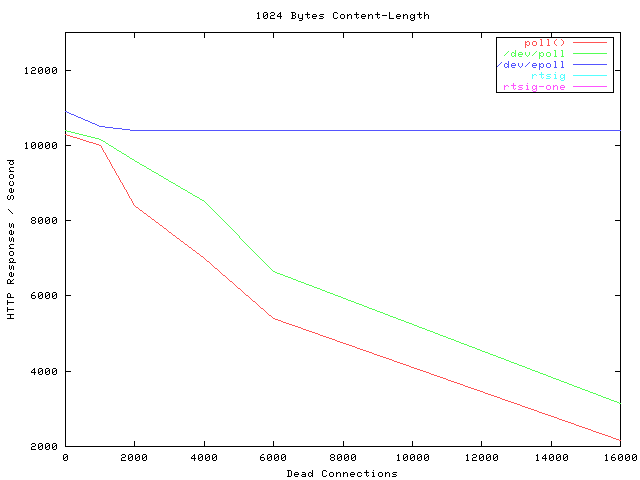
linux内核之select/poll/epoll
一些主流应用IO多路复用技术,突破高并发问题,如nginx、redis、netty,分布式服务框架dubbo,大数据组件hadoop、spark、flink、hbase纷纷使用netty作为网络通信组件。 一、背景:C10K问题 The C10K problem 最早被Dan …...

文件流下载
文件下载 后端传给前端json数据流,前端拿到之后存放在自定义的文件中import axios from "axios"; import qs from "query-string"; import {Notification } from "@arco-design/web-vue"; // 接口中需要含有文件名fileName export function dow…...

C语言模拟实现:atoi函数
在实现atoi之前我们先来了解一下atoi函数的作用是什么: 目录 1.实例演示 2.模拟实现 2.1 判断是否为空指针 2.2判断是否为空字符串 2.3判断正负号 2.4判断非数字字符 2.5判断是否越界 2.6完整代码 1.实例演示 //实例演示 #include <stdio.h> #include …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
