31.下一个排列
1. 题目
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
2. 解题思路
我们可以将该问题形式化地描述为:给定若干个数字,将其组合为一个整数。如何将这些数字重新排列,以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数,则输出最小的整数。
那么就应该尽量少动前面的数,因为前面的数是高位,尽量动后面的低位数;
分析过程
具体怎么动呢?
-
只需要 将后面的「大数」与前面的「小数」交换,就能得到一个更大的数。比如
123456,将5和6交换就能得到一个更大的数123465。 -
我们还希望下一个数 增加的幅度尽可能的小,比如
123465,下一个排列应该把5和4交换而不是把6和4交换 -
将「大数」换到前面后,需要将「大数」后面的所有数 重置为升序,升序排列就是最小的排列。以
123465为例:首先按照上一步,交换5和4,得到123564;然后需要将5之后的数重置为升序,得到123546。显然123546比123564更小;
实现过程
- 从后向前 查找第一个 相邻升序 的元素对
(i,j),满足A[i] < A[j]。此时[j,end)必然是降序 - 在
[j,end)从后向前 查找第一个满足A[i] < A[k]的k。 - 将
A[i]与A[k]交换 - 可以断定这时
[j,end)必然是降序,逆置[j,end),使其升序 - 如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
3. C++代码
class Solution {
public:void nextPermutation(vector<int>& nums) {int n = nums.size();for (int i=n-2; i>=0; i--){int j = i+1;if (nums[j] > nums[i]){for (int k=n-1; k>=j; k--){if (nums[k] > nums[i]){swap(nums[i], nums[k]);reverse(nums.begin()+j, nums.end());return;}}}}reverse(nums.begin(), nums.end());return;}
};
相关文章:

31.下一个排列
1. 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地&…...

ToBeWritten之理解嵌入式Web HTTP协议
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

顶级程序员的成长之路1
本文关注的问题是程序员的水平究竟应该按照什么样的不同层级而逐渐提高?或者说,在学习编程的过程中,每一个阶段究竟应当设定什么样的目标才比较合理?本文的内容主要借鉴了周伟明先生的专栏文章《程序员的十层楼》[86]。注意本文讨…...

第三代api自动化测试框架使用教程(pytest+allure+sql+yaml)
使用教程一、配置1、环境配置2、框架配置3、启动入口二、用例编写1、用例模板2、参数依赖写法2、函数(方法插件)写法3、接口上传文件和表单参数4、接口上传json参数5、接口无数据填写6、code断言7、body断言7、json断言8、sql断言9、完整断言写法&#x…...

Qt——实现一个获取本机网络信息的界面
效果展现 代码实现 networkinformation.h: #ifndef NETWORKINFORMATION_H #define NETWORKINFORMATION_H#include <QMainWindow> #include <QLabel> #include <QLineEdit> #include <QPushButton>class NetworkInformation : public QMai…...
全面深入了解接口自动化,看完还不会我报地址
一、自动化分类 (1)接口自动化 python/javarequestsunittest框架来实现 python/javaRF(RobotFramework)框架来实现——对于编程要求不高 (2)Web UI功能自动化 python/javaseleniumunittestddtPO框架来实…...

Python 小型项目大全 61~65
六十一、ROT13 密码 原文:http://inventwithpython.com/bigbookpython/project61.html ROT13 密码是最简单的加密算法之一,代表“旋转 13 个空格”密码将字母A到Z表示为数字 0 到 25,加密后的字母距离明文字母 13 个空格: A变成N&…...
Hlog
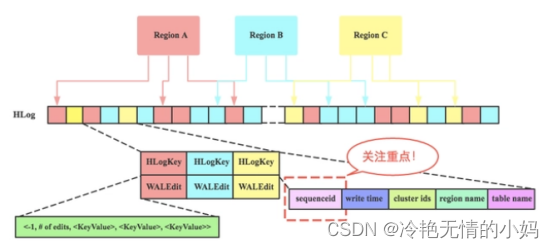
Hlog 简介 Hlog是Hbase实现WAL(Write ahead log )方式产生的日志信息 , 内部是一个简单的顺序日志。每个RegionServer对应1个Hlog(备注:1.X版本的可以开启MultiWAL功能,允许对应多个Hlog),所有对于该RegionServer的写入都会被记录到Hlog中。H…...

学编程应该选择什么操作系统?
今天来聊一个老生常谈的问题,学编程时到底选择什么操作系统?Mac、Windows,还是别的什么。。 作为一个每种操作系统都用过很多年的程序员,我会结合我自己的经历来给大家一些参考和建议。 接下来先分别聊聊每种操作系统的优点和不…...
Oracle基础部分二(伪列/表、单个函数、空值处理、行列转换、分析函数、集合运算)
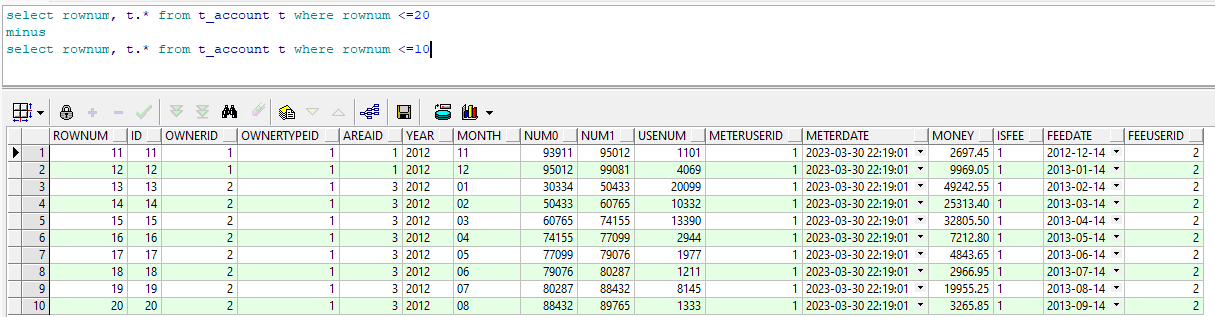
Oracle基础部分二(伪列/表、单个函数、空值处理、行列转换、分析函数、集合运算)1 伪列、伪表1.1 伪列1.2 伪表2 单个函数2.1 常用字符串函数2.1.1 length() 询指定字符的长度2.1.2 substr() 用于截取字符串2.1.3 concat() 用于字符串拼接2.2 常用数值函…...

c/c++:原码,反码,补码和常见的数据类型取值范围,溢出
c/c:原码,反码,补码和常见的数据类型取值范围,溢出 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,此时学会c的话, 我所知道的周边的会c的同学,可手握…...

Java题目训练——年终奖和迷宫问题
目录 一、年终奖 二、迷宫问题 一、年终奖 题目描述: 小东所在公司要发年终奖,而小东恰好获得了最高福利,他要在公司年会上参与一个抽奖游戏,游戏在一个6*6的棋盘上进行,上面放着36个价值不等的礼物, 每…...
ORACLE EBS系统应用基础概述(1)
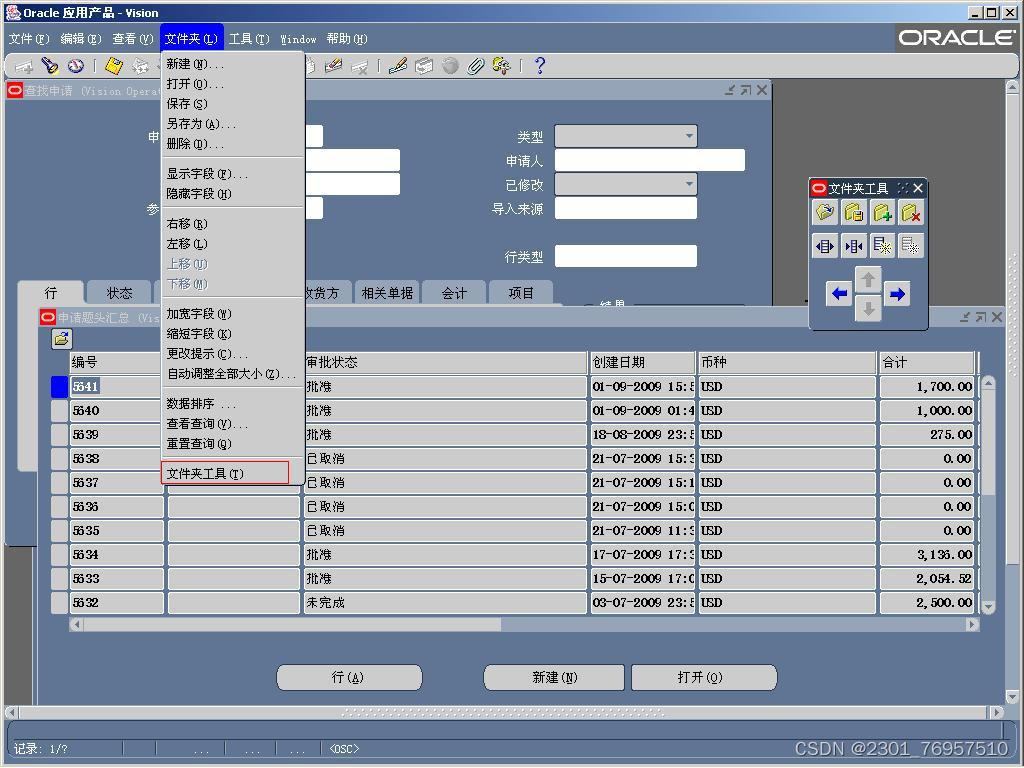
一、前言 有网友在论坛发帖惊呼:好不容易把EBS系统安装好了,进去一看傻眼了,不知道从哪儿下手?发出惊叹的这位网友所遇到的问题,实际上也是很多人曾经遇到或正在遇到的问题。长期以来,国内的非专业人士&am…...

电子科技大学信息与通信工程学院2023考研复试总结
一、笔试 笔试主要考察数字逻辑(数电)的相关知识,满分200分,需要复习的内容不多且知识点比较集中。根据考场上实际感受,题目难度不大但是题量稍大,2h完成试卷几乎没有多少剩余时间。笔试的体型分为填空题、…...
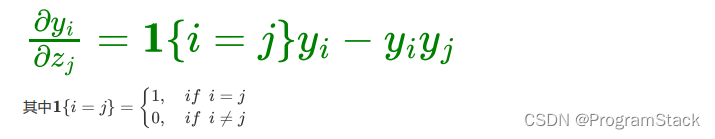
神经网络激活函数
神经网络激活函数神经网络激活函数的定义为什么神经网络要用激活函数神经网络激活函数的求导Sigmoid激活函数Tanh激活函数Softmax激活函数神经网络激活函数的定义 所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数…...

2.C 语言基本语法
文章目录二、C 语言基本语法1.语句2.表达式3.语句块4.空格5.注释6.printf()函数基本用法7.占位符8.输出格式10.标准库,头文件提示:以下是本篇文章正文内容,下面案例可供参考 二、C 语言基本语法 1.语句 C语言的代码由一行行语句࿰…...

Qt 6.5 LTS 正式发布
Qt 6.5 LTS 已正式发布。此版本为图形和 UI 开发者以及应用程序后端引入了许多新功能,还包含许多修复和通用的改进。Qt 6.5 将成为商业许可证持有者的长期支持 (LTS) 版本。 部分更新亮点: 改进主题和样式 使用 Qt 6.5,应用程序能够便捷地支持…...

Linux权限提升—定时任务、环境变量、权限配置不当、数据库等提权
Linux权限提升—定时任务、环境变量、权限配置不当、数据库等提权1. 前言1.1. 如何找编译好的EXP2. 定时任务提权2.1. 查看定时任务2.2. 通配符注入提权2.2.1. 创建执行脚本2.2.2. 创建定时任务2.2.3. 查看效果2.2.4. 提权操作2.2.4.1. 切换普通用户2.2.4.2. 执行命令2.2.4.3. …...

Python爬虫——使用requests和beautifulsoup4库来爬取指定网页的信息
以下是一个简单的Python代码,使用requests和beautifulsoup4库来爬取指定网页的信息: import requests from bs4 import BeautifulSoupurl "https://example.com"# 发送GET请求,获取网页内容 response requests.get(url)# 将网页内…...
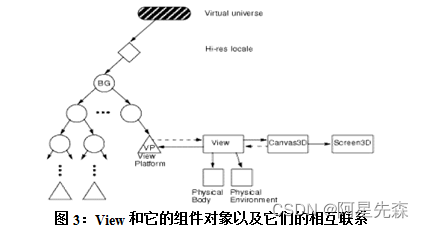
基于Java3D的网络三维技术的设计与实现
3D图形技术并不是一个新话题,在图形工作站以至于PC机上早已日臻成熟,并已应用到各个领域。然而互联网的出现,却使3D图形技术发生了和正在发生着微妙而深刻的变化。Web3D协会(前身是VRML协会)最先使用Web3D术语…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
