凑微分练习
前言
在学习第一类换元法(凑微分法)时,我们常常需要凑微分。为了更加熟练地运用凑微分法,下面有几道凑微分例题供大家练习。
记住df(x)=f′(x)dxdf(x)=f'(x)dxdf(x)=f′(x)dx
例题1
- dx=‾d(ax)dx=\underline{\quad}d(ax)dx=d(ax)
- dx=‾d(6x−4)dx=\underline{\quad}d(6x-4)dx=d(6x−4)
- xdx=‾d(x2)xdx=\underline{\quad}d(x^2)xdx=d(x2)
- xdx=‾d(1−x2)xdx=\underline{\quad}d(1-x^2)xdx=d(1−x2)
- x2dx=‾d(4x3+3)x^2dx=\underline{\quad}d(4x^3+3)x2dx=d(4x3+3)
答案:(1)a(2)16(3)12(4)−12(5)112(1)a \qquad(2)\dfrac 16 \qquad(3)\dfrac 12\qquad (4)-\dfrac 12 \qquad(5)\dfrac {1}{12}(1)a(2)61(3)21(4)−21(5)121
例题2
- exdx=‾d(3ex)e^xdx=\underline{\quad}d(3e^x)exdx=d(3ex)
- e2xdx=‾d(e2x)e^{2x}dx=\underline{\quad}d(e^{2x})e2xdx=d(e2x)
- ex2dx=‾d(ex2+3)e^{\frac x2}dx=\underline{\quad}d(e^{\frac x2}+3)e2xdx=d(e2x+3)
- 1xdx=‾d(3ln∣x∣)\dfrac 1xdx=\underline{\quad}d(3\ln|x|)x1dx=d(3ln∣x∣)
- 2xdx=‾d(5−4ln∣x∣)\dfrac 2xdx=\underline{\quad}d(5-4\ln|x|)x2dx=d(5−4ln∣x∣)
答案:(1)13(2)12(3)2(4)13(5)−12(1)\dfrac 13 \qquad(2) \dfrac 12 \qquad(3)2 \qquad(4)\dfrac 13 \qquad(5)-\dfrac 12(1)31(2)21(3)2(4)31(5)−21
例题3
- sinxdx=‾d(cosx)\sin xdx=\underline{\quad}d(\cos x)sinxdx=d(cosx)
- cos23xdx=‾d(sin23x)\cos \dfrac 23xdx=\underline{\quad}d(\sin \dfrac 23x)cos32xdx=d(sin32x)
- 11−x2dx=‾d(1−arcsinx)\dfrac{1}{\sqrt{1-x^2}}dx=\underline{\quad}d(1-\arcsin x)1−x21dx=d(1−arcsinx)
- 11+9x2dx=‾d(arctan3x)\dfrac{1}{1+9x^2}dx=\underline{\quad}d(\arctan 3x)1+9x21dx=d(arctan3x)
- x1−x2dx=‾d(1−x2)\dfrac{x}{\sqrt{1-x^2}}dx=\underline{\quad}d(\sqrt{1-x^2})1−x2xdx=d(1−x2)
答案:(1)−1(2)32(3)−1(4)13(5)−1(1)-1 \qquad(2)\dfrac 32 \qquad(3)-1 \qquad(4)\dfrac 13 \qquad(5)-1(1)−1(2)23(3)−1(4)31(5)−1
相关文章:

凑微分练习
前言 在学习第一类换元法(凑微分法)时,我们常常需要凑微分。为了更加熟练地运用凑微分法,下面有几道凑微分例题供大家练习。 记住df(x)f′(x)dxdf(x)f(x)dxdf(x)f′(x)dx 例题1 dx‾d(ax)dx\underline{\quad}d(ax)dxd(ax)dx‾…...
JavaWeb——多线程使用哈希表
目录 一、HashMap 1、定义 二、HashTable 1、定义: 2、区别: 三、ConcurrentHashMap 1、定义: 2、优化 (1)、加锁粒度不同——触发锁冲突的频率不同 (2)、充分利用CAS机制——无锁编程…...

anaconda permission denied
可能是路径不对 我的是只写了dir,没写文件名,而我要的是某个文件的路径,所以就报这个错。 具体,我需要某个权重的路径,比如pytorch_resnet50.pth,但我只写了这个权重所在的dir,比如F:/software/…...
蓝桥杯带刷,带刷!!!
A:::::::::::::::::::::::::::::::::::m计划(双指针,滑动窗口,倍增) 题目描述 小明是个鹅卵石收藏者,从小到大他一共收藏了 nn 块鹅卵石,编号分别为 1∼n,价值分别为 a1,a2&…...
第03讲:MinIO分布式文件服务器
一、什么是MinIO Minio 是个基于 Golang 编写的开源对象存储套件,虽然轻量,却拥有着不错的性能。 官网地址:MinIO | High Performance, Kubernetes Native Object Storageopen in new window官网文档地址:MinIO | The MinIO Qui…...

WireShark
wireshark 常用命令: frame.len 帧数据总长度:包含MAC头IP头UDP头UDP数据 eg: 1、 重传命令的长度是62, Frame.len 62 2、 长度大于200的包,frame.len > 200 3、 长度小于80的包,frame.len < 80 Ip.src 数据包的发送源IP地…...

Thinkphp 6.0多语言
本节课我们来学习一下如何配置的多语言功能,并实现调用方法。 一.多语言 1. 如果要开启多语言切换功能,中间件定义文件 middleware.php 开启; // 多语言加载 \think\middleware\LoadLangPack::class, 2. 配置文件在 config/lang…...

生成式AI已形成全球性“AI再造业务”趋势
3月28日至31日,博鳌亚洲论坛2023年年会在海南举行。实体经济与数字经济如何融合发展,产业数字化如何加速向深层次拓展,生成式AI会给产业经济带来哪些变革?这些话题成为今年论坛热点。 百度集团执行副总裁、百度智能云事业群总裁沈…...
kubesphere 安装 skywalking
kubesphere 安装 skywalking 前言 在测试ELK过程中,框架内部使用skywalking来插入的traceId,没有服务端导致Ignored_Trace,先安装下试试skywalking使用效果,后面考了替换为Tlog 先来安装skywalking… 1. 导入helm原 地址&#x…...

乐鑫 × 全国大学生物联网设计竞赛|探究基于 ESP32-S3 的农业革新应用
2023 年全国大学生物联网设计竞赛(下简称“竞赛”)现已官宣启幕!乐鑫科技 (688018.SH) 作为竞赛金牌合作伙伴,将为同学们带来基于 AI SoC ESP32-S3 的独立竞赛任务,并全程提供软硬件开发资源、技术培训…...
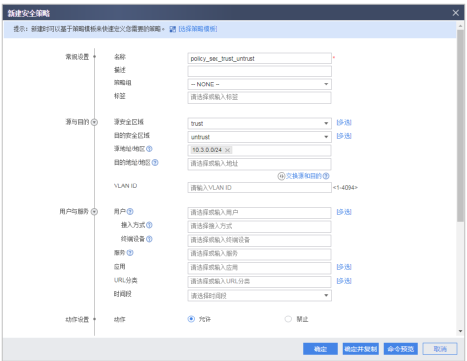
【技术分享】华为防火墙多出口接入到Internet
组网需求 如图1所示,FW作为安全网关部署在网络出口,企业分别从ISP1和ISP2租用一条链路。 企业希望访问Server 1的报文从ISP1链路转发,访问Server 2的报文从ISP2链路转发。 当其中一条链路故障时,后续流量可以通过另一条链路转发…...
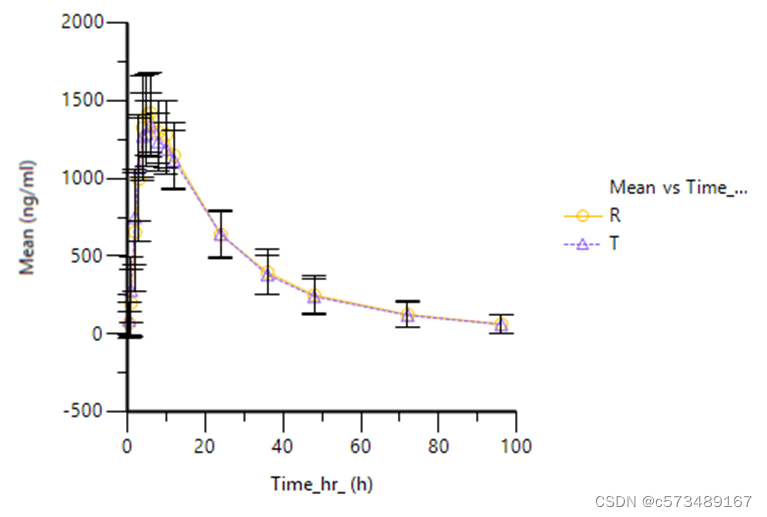
Winnolin绘制药时曲线图C-T
文章目录前言一、各受试者C-T图1.导入数据2.设置-运行2.查看结果,修改参数二、各制剂C-T图1.导入数据2.设置-运行2.查看结果,修改参数三、平均C-T图1.计算统计量2.设置统计量计算参数(Set Up)3.绘图XY Plot4.查看结果,…...

Kafka系列——详解如何使用和配置生产者实现可靠的消息发送
在可靠的系统里使用生产者 即使我们尽可能把 broker 配置得很可靠,但如果没有对生产者进行可靠性方面的配置,整个系统仍然有可能出现突发性的数据丢失。 比如下面的两个例子: (一)为 broker 配置了 3 个副本࿰…...
wordpres漏洞扫描器——wpscan
WordPress 使用PHP语言开发的博客平台 WordPress是使用PHP语言开发的博客平台,用户可以在支持PHP和MySQL数据库的服务器上架设属于自己的网站。也可以把 WordPress当作一个内容管理系统(CMS)来使用。 WordPress是一款个人博客系统,…...
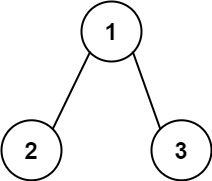
代码随想录_二叉树_leetcode112、113
leetcode112 路径总和 112. 路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返…...

mongo-db相关方法
一、参数 名称描述db.adminCommand()针对admin数据库运行命令。db.aggregate()运行不需要基础集合的管理/诊断管道。db.cloneDatabase(hostname)不推荐使用。当针对MongoDB 4.0或更早版本运行时,将数据库从远程主机复制到当前主机。针对MongoDB 4.2或更高版本运行时…...
《Vue3实战》 第二章 创建项目和目录结构
1、创建项目 1.1、命令格式:vue create 项目名称 vue create vue3_example0011.2、运行项目 npm run serve1.2.1、增加run命令 启动时想修改命令,例如: npm run dev1、找到项目根路径下的package.json文件; 2、找到【scripts…...

13433元!上海一季度平均薪酬出炉!你拖后腿了吗?(附招聘岗位)
2023年第一季度智联招聘, 发布《中国企业招聘薪酬报告》, 显示上海平均招聘薪酬为 13433元/月!!! 13433元/月!!! 13433元/月!!! ☟ ☟ ☟ 同…...

leetcode剑指 Offer 16. 数值的整数次方
题目描述解题思路执行结果leetcode .题目描述 实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。 示例 1: 输入:x 2.00000, n 10 输出:1…...
漏洞挖掘相关-信息收集
一、常见端口以及漏洞 1.FTP:文件传输协议 TCP端口20、21,20用于传输数据,21用于传输控制信息 (1) ftp基础爆破: owasp的Bruter,hydra以及msf中的ftp爆破模块。 (2) ftp匿名访问:用户名: anonymous密码:为空或者任意邮箱 (3) vsftpd后门: …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
