代码随想录算法训练营第四十九天 | 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
打卡第49天,买卖股票系列了
今日任务
● 121. 买卖股票的最佳时机
● 122.买卖股票的最佳时机II
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
我的题解
贪心做法,一边最小的买入,一边最大的收益,卖出一定在买入后面
class Solution {
public:int maxProfit(vector<int>& prices) {int low = INT_MAX;int res = 0;for(int i = 0; i < prices.size(); i++) {low = min(low, prices[i]);res = max(res, prices[i] - low);}return res;}
};
代码随想录
动态规划思路:
- dp以及下标的定义
dp[i][0]表示第i天持有股票所得最大现金
dp[i][1]表示第i天不持有股票所得最大现金 - 递推公式
dp[i][0]=max(dp[i−1][0],−prices[i]);//持有股票可能是i−1天前持有,也有可能是当天买入dp[i][0] = max(dp[i - 1][0], -prices[i]); //持有股票可能是i-1天前持有,也有可能是当天买入dp[i][0]=max(dp[i−1][0],−prices[i]);//持有股票可能是i−1天前持有,也有可能是当天买入
dp[i][1]=max(dp[i−1][1],dp[i][0]+prices[i]);//不持有股票可能是i−1天前就不持有,也有可能是当天卖出dp[i][1] = max(dp[i - 1][1], dp[i][0] + prices[i]);//不持有股票可能是i-1天前就不持有,也有可能是当天卖出dp[i][1]=max(dp[i−1][1],dp[i][0]+prices[i]);//不持有股票可能是i−1天前就不持有,也有可能是当天卖出 - 初始化
dp[0][0] 第一天持有股票,那就是第一天买入 -prices[0];
dp[0][1] 第一天不持有股票,初始化为0 - 遍历顺序
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。
class Solution {
public:int maxProfit(vector<int>& prices) {int size = prices.size();vector<vector<int>> dp(size, vector<int>(2, 0)); //dp[i][0] 当天持有股票所得最大现金,当天不持有股票的所得最大现金dp[0][0] -= prices[0]; dp[0][1] = 0;for(int i = 1; i < size; i++) {dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i][0] + prices[i]);}return dp[size - 1][1];}
};
122.买卖股票的最佳时机II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
我的题解
无限次买进卖出
class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for(int i = 1; i < prices.size(); i++) {res += max(prices[i] - prices[i - 1], 0);}return res;}
};
代码随想录
因为本题的股票可以买卖多次! 所以买入股票的时候,可能会有之前买卖的利润即:dp[i - 1][1],所以dp[i - 1][1] - prices[i]。
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2,0));dp[0][0] -= prices[0]; dp[0][1] = 0;for(int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[n - 1][1];}
};
相关文章:

代码随想录算法训练营第四十九天 | 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
打卡第49天,买卖股票系列了 今日任务 ● 121. 买卖股票的最佳时机 ● 122.买卖股票的最佳时机II 121. 买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票&#x…...

【职场篇】程序员是否吃青春饭?程序员在35岁之后是否需要转行?
你们好 那么众所周知呢像空姐 还有模特这种职业呢 都是吃青春饭的 那么到了一定年龄呢 他们可能就不做这一行了 那么其实程序员这个职业呢 有的人认为他也是吃青春饭的 普遍人都认为呢 如果程序员做到35岁呢 没有转管理岗位 可能以后就没有什么前途了 可能就要考虑换别的行业了…...
( “树” 之 DFS) 226. 翻转二叉树 ——【Leetcode每日一题】
226. 翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1] 示例 2: 输入:root [2,1,3] 输出:[…...

实验7---myBatis和Spring整合
实验七 myBatis和Spring整合 一、实验目的及任务 通过该实验,掌握mybatis和spring整合方法,掌握生成mapper实现类的两种生成方式。 二、实验环境及条件 主机操作系统为Win10,Tomcat,j2sdk1.6或以上版本。 三、实验实施步骤 略 四、实验报告内…...

DJ3-4 传输层(第四节课)
目录 一、TCP 概述 二、TCP 报文段的首部字段格式 三、TCP 往返时延的估计和超时 1. 估计往返时间 2. RTT 估计例子 3. 估计往返时间的偏差 4. 设置重传超时间隔 一、TCP 概述 全双工服务:允许在同一时间同一连接上,数据能够双向传输。注意&#…...

2023爱分析·商业智能应用解决方案市场厂商评估报告:数聚股份
目录 1. 研究范围定义 2. 商业智能应用解决方案市场分析 3. 厂商评估:数聚股份 4. 入选证书 1. 研究范围定义 商业智能(BI)是在实现数据集成和统一管理的基础上,利用数据存储和处理、分析与展示等技术,满足企…...

Kotlin方法执行顺序
方法的执行顺序 主构造函数init代码块次构造函数...
Ubuntu系统配置SonarQube + cppcheck + Jenkins
SonarQube1. postgresql安装及配置1.1 安装postgresql1.2 创建sonarqube用户1.3 设置数据库2. 安装sonarqube2.1 设置sonarqube2.2 修改sonarqube目录权限2.3 sonar.properties2.4 设置systemd管理sonarqube2.5 web3. 配置sonarscanner3.1 下载3.2 配置4. 配置cppcheck4.1 下载…...

Spring @Valid 不生效 问题记录
校验的简单使用: 在Spring中,我们可以使用Valid注解对实体进行校验。在Controller的方法参数中添加Valid注解,然后在实体类的属性上添加校验注解,例如NotNull、Size等。例如: RestController public class UserContr…...

五步教你如何注册一个公司网站
在今天的数字化时代,每个公司都需要一个强大的线上存在感。注册一个公司网站是实现这一目标的第一步。但是,对于许多公司而言,这个过程可能有些困难。因此,在本文中,我将介绍一个五步计划,让您轻松注册一个…...

CSS绘制气泡对话框样式(有边框)
1、效果图 2、难点和思路 难点:上面那个带边框的小三角不好实现 思路:画两个不同大小的div,使其基本重叠(两个大小不同,不完全重叠,让红色的露出一点边边),让白色div放到最上层&…...
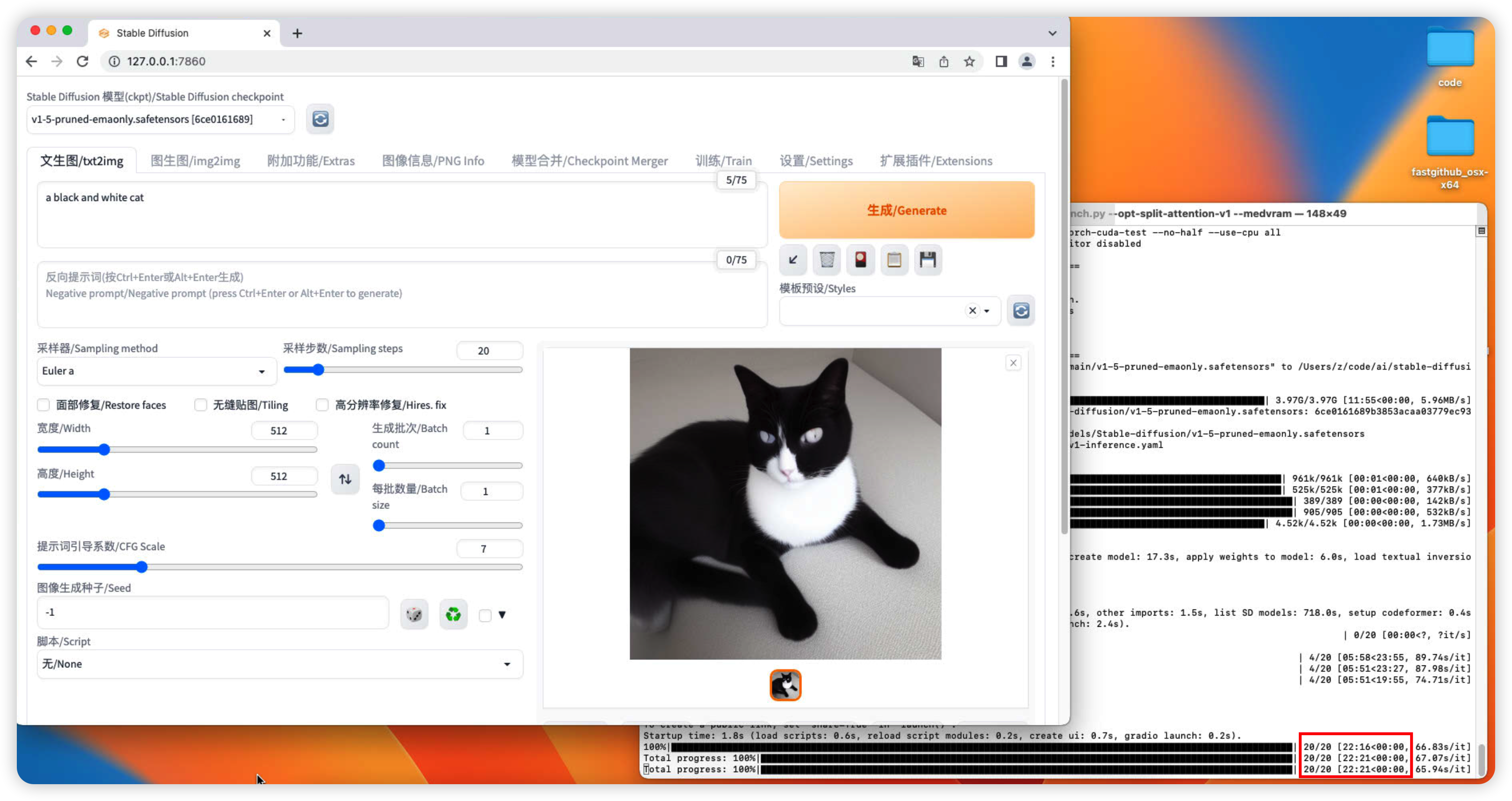
12款 Macmini A1347 跑 Stable Diffusion,20多分钟一张图
设备 2012款 Macmini A1347 12款 mini A1347 跑 Stable Diffusion 要20多分钟一张图 来欣赏一下20分钟画出来的图片 a black and white cat 环境:...
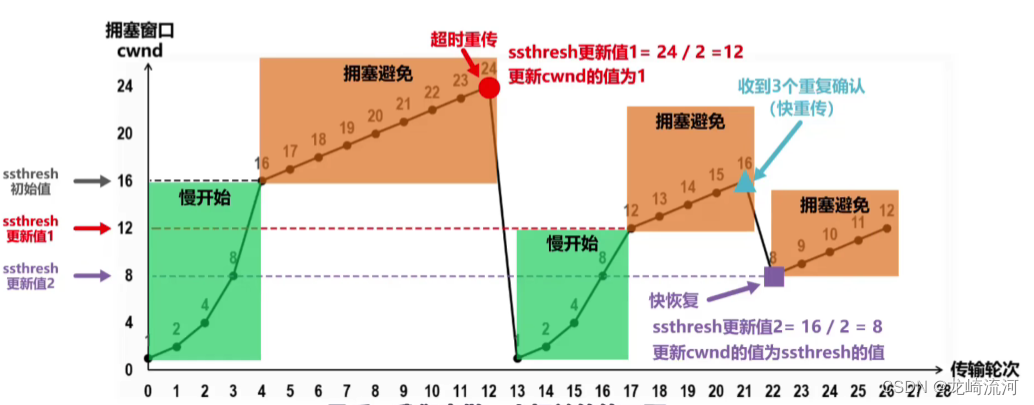
流量控制和拥塞控制的原理和区别
文章目录先介绍下重传机制和滑动窗口超时重传快速重传SACK方法Duplicate SACK滑动窗口发送方缓存窗口接收方缓存窗口流量控制小结拥塞控制慢开始算法拥塞避免算法快重传快恢复先介绍下重传机制和滑动窗口 超时重传 重传机制的其中一个方式,就是发送数据时…...

金融机构断卡行动中外部数据
“断卡行动”,近几年逐渐走入大众视野,是国家在从根源上整治网络及金融犯罪层面的重大举措。相信很多朋友在日常生活中已经有所体会了,比如我们在办理电话卡及银行卡的时候要经过很多审核机制,同时发卡后还会限制卡片的一些转账等…...

携程总监的单元测试是怎么样写的?
大家都知道,开发软件的时候为代码编写单元测试是很好的。但实际上,光有测试还不够,还要编写好的测试,这同样重要。 要做到这一点,考虑遵循一些固执的原则,对测试代码给予一些关爱: 1. 保持测试…...

算法每日一题:P2089 烤鸡 -DFS练习
😚一个不甘平凡的普通人,日更算法学习和打卡,期待您的关注和认可,陪您一起学习打卡!!!😘😘😘 🤗专栏:每日算法学习 💬个人…...

Spring中的循环依赖是什么?如何解决它?
循环依赖是指两个或多个Bean之间相互依赖,导致它们无法被正确地初始化。在Spring中,当两个或多个Bean之间存在循环依赖时,Spring容器无法决定哪个Bean应该先初始化,因此会抛出BeanCurrentlyInCreationException异常,从…...
不良事件报告系统源码,PHP医院安全(不良)事件报告系统源码,在大型医院稳定运行多年
PHP医院安全(不良)事件报告系统源码,不良事件系统源码,有演示,在大型医院稳定运行多年。 系统技术说明 技术架构:前后端分离,仓储模式 开发语言:PHP 开发工具:VSco…...
——排序 order by)
MySQL 查询常用操作(3)——排序 order by
MySQL中常用的查询操作,首先是能直接从表中直接取出数据,接着能对查询结果做一些简单的处理,比如去重等,然后是根据条件查询数据,包括精准查询、模糊查询以及按照数据的某个范围或者指定多个指标进行查询,值…...
)
Android Jetpack 从使用到源码深耕【数据库注解Room 从实践到原理 】(二)
上文,我们通过一个简单的sqlite应用实例,引入了Room,知道了Room使用的便捷和好处。然后用Room的方式,重新实现了应用实例中的场景,在这个过程中,我们结合自己已有的知识体系,从使用代码入手,对Room的实现原理,进行了猜想和简单的验证。 Room实现原理,是否真如我们猜想…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
