最速下降法
首先,计算函数f的梯度向量:∇f(x1,x2)=[2x150x2]\nabla f(x_1,x_2) = \begin{bmatrix}2x_1\\50x_2\end{bmatrix}∇f(x1,x2)=[2x150x2]
然后,选择一个初始点(x10,x20)(x_1^0,x_2^0)(x10,x20),比如(0,0)(0,0)(0,0)。
接下来,根据最速下降法的迭代公式进行迭代,直到收敛为止:
[x1k+1x2k+1]=[x1kx2k]−αk∇f(x1k,x2k)\begin{bmatrix}x_1^{k+1}\\x_2^{k+1}\end{bmatrix} = \begin{bmatrix}x_1^{k}\\x_2^{k}\end{bmatrix} - \alpha_k \nabla f(x_1^k,x_2^k)[x1k+1x2k+1]=[x1kx2k]−αk∇f(x1k,x2k)
其中,αk\alpha_kαk是步长(学习率),通常需要通过试错法进行选取,以确保迭代的稳定性和收敛性。
在本例中,由于f(x1,x2)f(x_1,x_2)f(x1,x2)是一个凸二次函数,因此最速下降法可以保证收敛,并得到全局最优解。
具体的迭代过程如下:
| kkk | (x1k,x2k)(x_1^k,x_2^k)(x1k,x2k) | ∇f(x1k,x2k)\nabla f(x_1^k,x_2^k)∇f(x1k,x2k) | αk\alpha_kαk | (x1k+1,x2k+1)(x_1^{k+1},x_2^{k+1})(x1k+1,x2k+1) | f(x1k+1,x2k+1)(x_1^{k+1},x_2^{k+1})(x1k+1,x2k+1) |
|---|---|---|---|---|---|
| 0 | (0,0) | (0,0) | 1 | (0,0) | 0 |
| 1 | (0,0) | (0,0) | 0.02 | (0,0) | 0 |
| 2 | (0,0) | (0,0) | 0.0008 | (0,0) | 0 |
| 3 | (0,0) | (0,0) | 0.000032 | (0,0) | 0 |
| 4 | (0,0) | (0,0) | 1.28E-6 | (0,0) | 0 |
| 5 | (0,0) | (0,0) | 5.12E-8 | (0,0) | 0 |
可以看到,最速下降法迭代6次后收敛,得到的最小值为0,也就是函数f(x1,x2)f(x_1,x_2)f(x1,x2)的最小值。请您继续提问,我将尽快回答您的问题。
相关文章:

最速下降法
首先,计算函数f的梯度向量:∇f(x1,x2)[2x150x2]\nabla f(x_1,x_2) \begin{bmatrix}2x_1\\50x_2\end{bmatrix}∇f(x1,x2)[2x150x2] 然后,选择一个初始点(x10,x20)(x_1^0,x_2^0)(x10,x20),比如(0,0)(0,0)(0,0)。 接…...
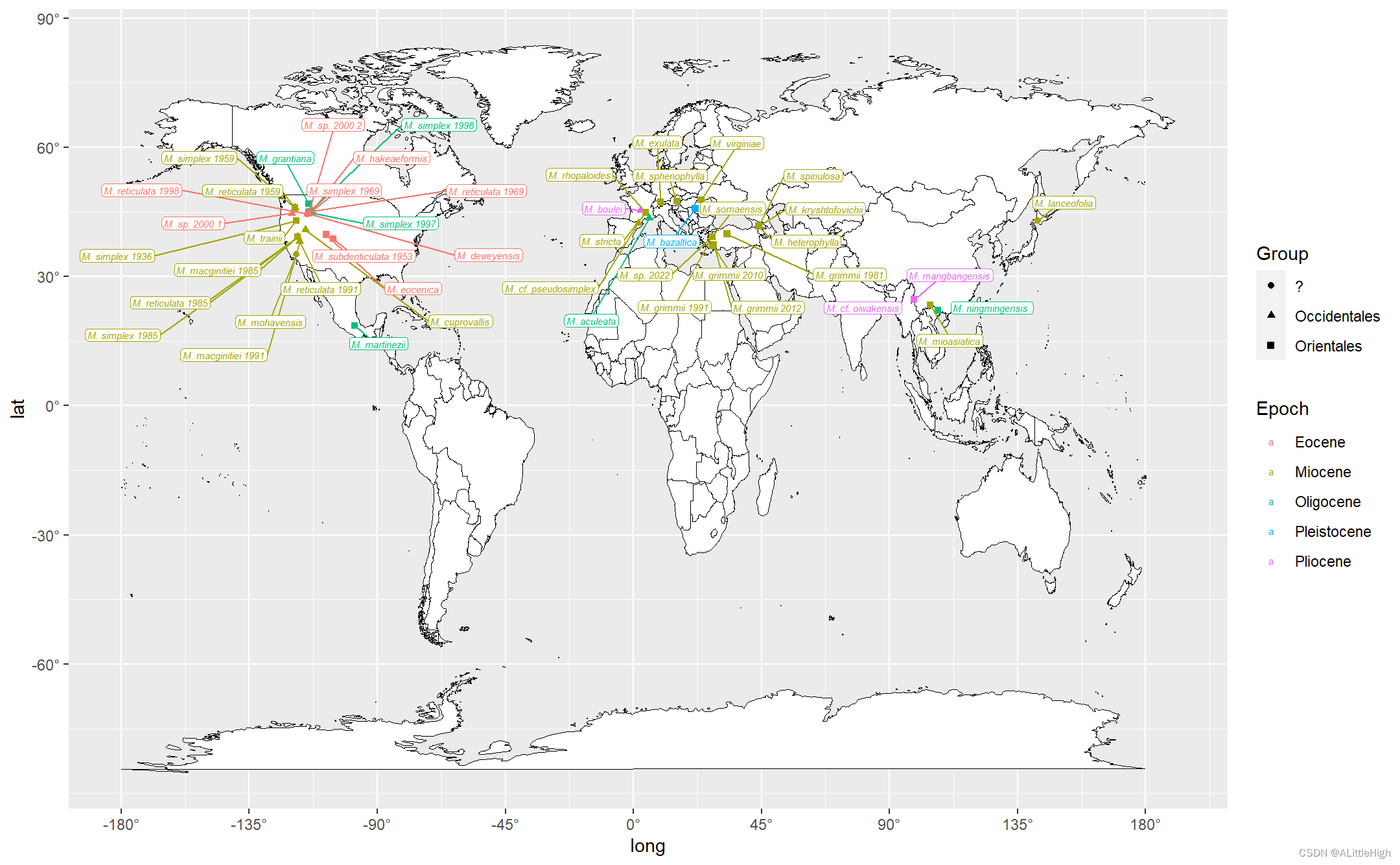
R语言实践——ggplot2+ggrepel绘制散点+优化注释文本位置
简介 书接adjustText实践——调整matplotlib散点图标签,避免重复 上文中,matplotlibadjustText对于我的实例来说并没有起到很好的效果。所以,博主决定在R中利用gglot2ggrepel绘制,期待效果。 操作过程 博主不常使用Rÿ…...
[TIFS 2022] FLCert:可证明安全的联邦学习免受中毒攻击
FLCert: Provably Secure Federated Learning Against Poisoning Attacks | IEEE Journals & Magazine | IEEE Xplore 摘要 由于其分布式性质,联邦学习容易受到中毒攻击,其中恶意客户端通过操纵其本地训练数据和/或发送到云服务器的本地模型更新来毒…...

css3关键帧动画
CSS3关键帧动画是一种在网页设计中常用的技术,通过使用CSS3的关键帧动画功能,可以实现网页上各种形式的动画效果,例如淡入淡出、滑动、旋转、缩放等,这些动画效果可以让网页更加生动有趣,吸引用户的注意力,…...
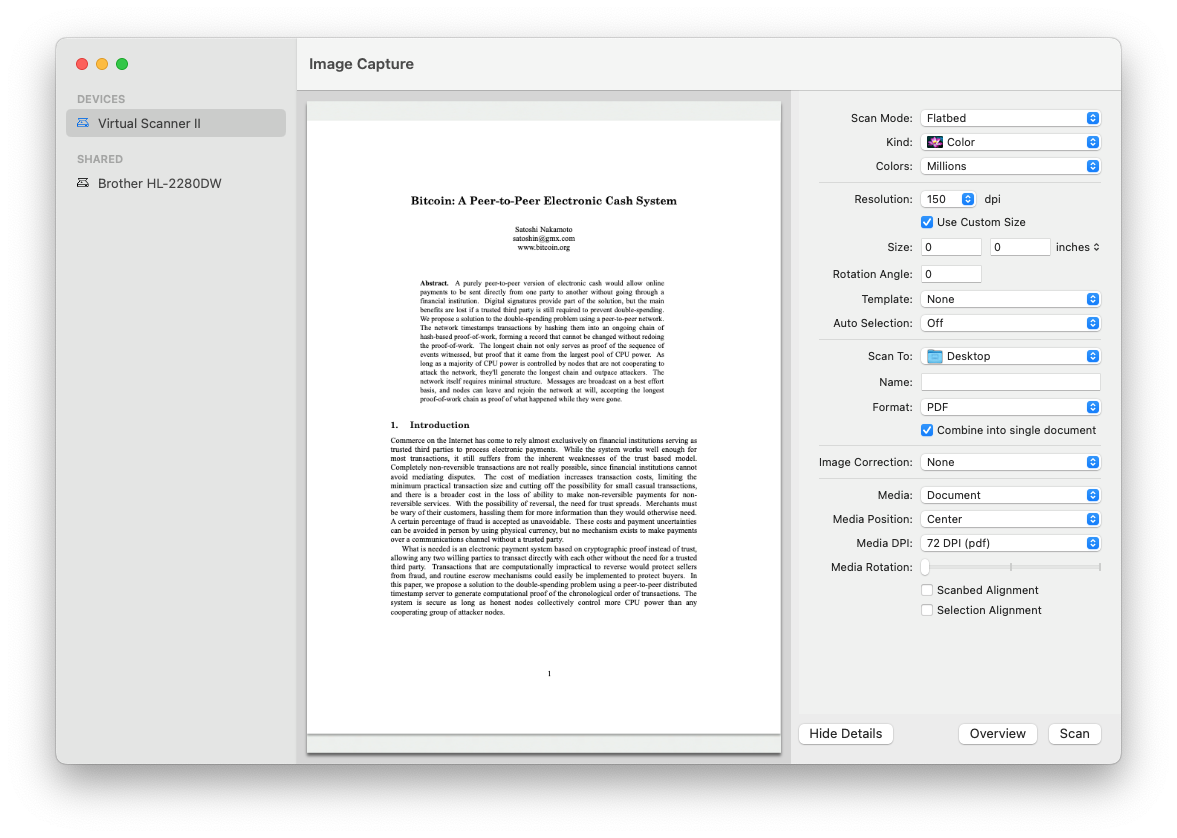
在 macOS Mojave 之后的每一个版本中都隐藏着比特币白皮书(Bitcoin Whitepaper)
今天我在尝试解决打印机故障问题时,发现了自2018年Mojave版本以来,macOS都附带了一份Satoshi Nakamoto(即中本聪)的比特币白皮书PDF副本[1]。 我已经询问了十几位使用Mac的朋友,他们都确认macOS里面有这个文件。这个文…...
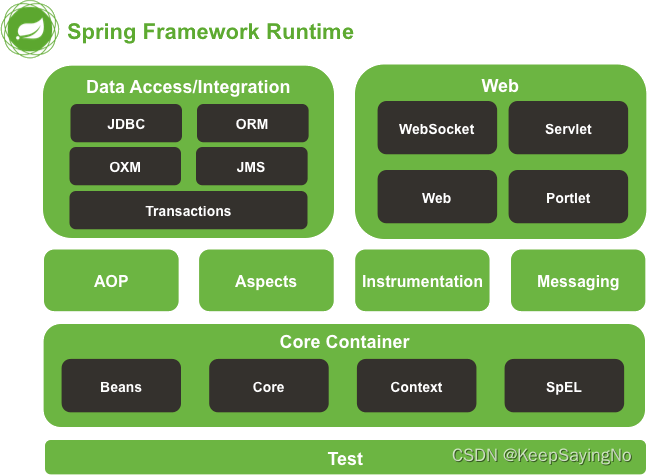
一文看懂SpringBoot操纵数据库
1.前言 很多同学进入公司就开始参与项目开发,大多数情况是对某个项目进行维护或者需求迭代,能够从0到1参与到项目中的机会很少,因此并没有多少机会了解某些技术的运行机制。换句话说,有的面试官在面试的时候就会探讨深层的技术问题…...

科普:java与C++的区别
Java与C是两种广泛使用的编程语言,它们在某些方面存在不同之处。本文将详细介绍Java与C的区别。 一、C与Java的历史 C语言是由Bjarne Stroustrup在20世纪80年代初期开发的一种面向对象编程语言,它是C语言的扩展。Java语言是由Sun Microsystems公司于20…...

突发!ChatGPT疯了!
数据智能产业创新服务媒体——聚焦数智 改变商业今天,笔者正常登录ChatGPT,试图调戏一下他。但是,突然震惊的发现,ChatGPT居然疯了。之所以说他是疯了,而不是崩溃了,是因为他还能回复我,但回…...
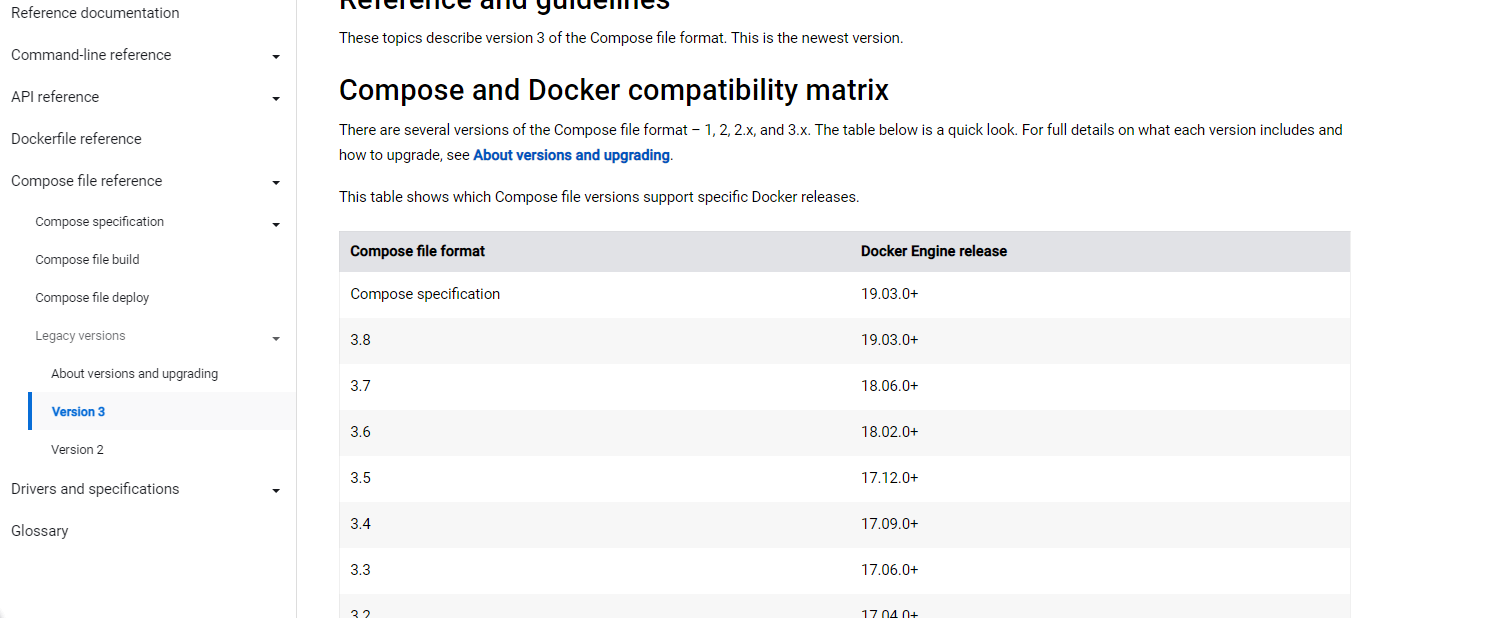
docker-compose容器编排使用详解+示例
文章目录一、docker-compose概述1、产生的背景2、核心概念3、使用的三个步骤4、常用命令二、下载安装1、官方文档2、下载3、卸载三、使用compose1、前置知识,将一个springboot项目打包为镜像2、编写docker-compose.yml文件3、启动docker-compose4、停止一、docker-c…...
可用的rtsp ,rtmp地址以及使用VLC和ffmpeg 播放视频流
可用的 rtmp地址: rtmp://ns8.indexforce.com/home/mystream 可用的 rtsp地址: rtsp://wowzaec2demo.streamlock.net/vod/mp4:BigBuckBunny_115k.mp4 可搭配VLC播放器使用,以及虚幻4 流媒体使用,实现直播效果 1.使用VLC 播放:https://www.vi…...
Python机器学习:朴素贝叶斯
前两天不知道把书放哪去了,就停更了一下,昨天晚上发现被我放在书包夹层里面了,所以今天继续开始学习。 首先明确一下啊,朴素贝叶斯是什么:朴素贝叶斯分类器是一种有监督的统计学过滤器,在垃圾邮件过滤、信…...

几个最基本软件的环境变量配置
在Windows中配置环境变量位置: 控制面板->系统和安全->系统。可以点击:“此电脑”->“属性”直接进入。 点击“高级系统设置”->【环境变量】。在这里可以看见用户变量和系统变量,如果你这台机器不是你一个人使用设置为用户变量…...

物业企业如何加快向现代服务业转型
近年来,随着人民生活水平的提高,人们对住宅质量提出更高的要求,在此前提下,全国各地涌现出了一些运用现代的计算机、控制与通信技术建设的智能化住宅小区。但是许多智能化住宅小区都存在建好了智能硬件环境却没有智能化的软件在上…...
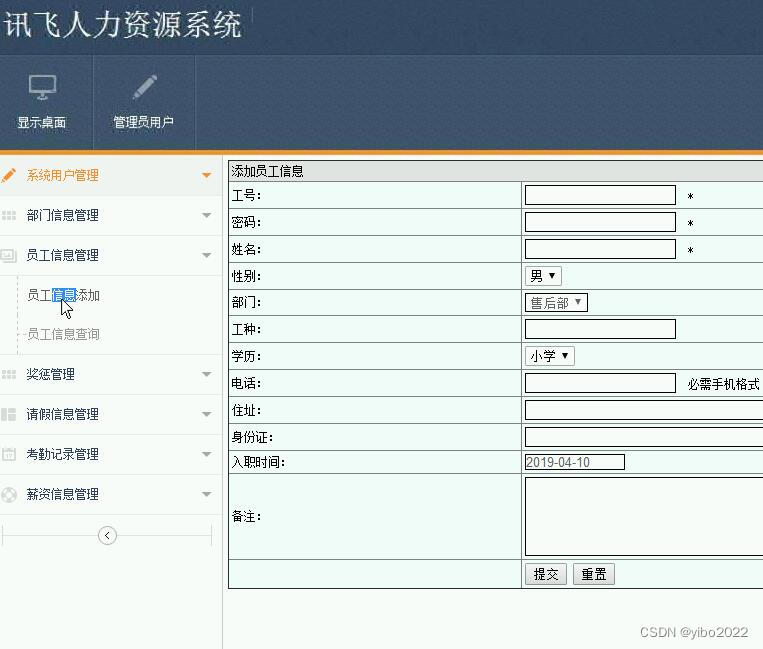
java ssm人力资源系统Y3程序
1.系统登录:系统登录是员工访问系统的路口,设计了系统登录界面,包括员工名、密码和验证码,然后对登录进来的员工判断身份信息,判断是管理员还是普通员工。 2.系统员工管理:不管是超级…...

leetcode重点题目分类别记录(三)动态规划深入与素数理论
文章目录动态规划背包问题01背包抽象出求解目标尝试进程子问题拆分基本情况根据拆分过程定义dp数组与转移方程遍历顺序与状态压缩模板归纳题目应用变种提升组合问题多维01背包有特殊限制的01背包完全背包打家劫舍股票系列子序列类数位dp动态规划 背包问题 01背包 有C0-Cx件物…...

面试篇-学习Java多线程编程必备:深入理解volatile与synchronized
1. 概述 1.1 Volatile概述 Volatile是Java中的一种轻量级同步机制,用于保证变量的可见性和禁止指令重排。当一个变量被声明为Volatile类型时,任何修改该变量的操作都会立即被所有线程看到。也就是说,Volatile修饰的变量在每次修改时都会强制…...

后端系列文章
后端系列文章目录 缘由:无聊了,写点博客玩玩 注:该系列文章纯属个人见解,漏洞百出,大家看个乐就行了,别当真! 私人博客 许小墨のBlog —— 菜鸡博客直通车 系列文章完整版,配图更多&…...

C++之AVL树
文章目录前言一、概念二、AVL树结点的定义三、AVL树的插入四、AVL树的旋转1.右单旋的情况以及具体操作抽象图h 0h 1h 2代码实现2.左单旋的情况以及具体操作抽象图代码实现3.右左双旋的情况以及具体操作抽象图h 0h 1h 23.左右双旋的情况以及具体操作抽象图5.总结6.完整实现…...
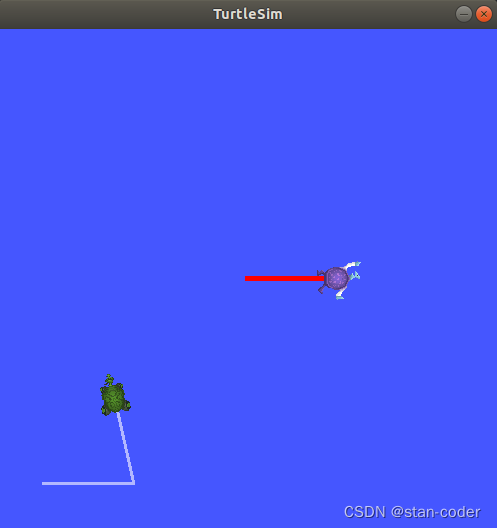
【ROS2指南-2】入门 turtlesim 和 rqt
目标:安装并使用 turtlesim 包和 rqt 工具为即将到来的教程做准备。 教程级别:初学者 时间: 15分钟 内容 背景 先决条件 任务 1 安装turtlesim 2 启动turtlesim 3 使用turtlesim 4 安装rqt 5 使用 rqt 6 重新映射 7 关闭turtlesim …...

Python 进阶指南(编程轻松进阶):四、起个好名字
原文:http://inventwithpython.com/beyond/chapter4.html 计算机科学中最困难的两个问题是命名事物、缓存失效引起错误."这个经典的笑话,出自利昂班布里克之手,并基于菲尔卡尔顿的一句话,包含了一个真理的核心:很…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
