SPOJ-NSUBSTR - Substrings(SAM求所有长度子串的最大出现次数)
NSUBSTR - Substrings
题面翻译
你得到了一个最多由 250000250000250000 个小写拉丁字母组成的字符串 SSS。定义 F(x)F(x)F(x) 为 SSS 的某些长度为 xxx 的子串在 SSS 中的最大出现次数。即 F(x)=max{times(T)}F(x)=max\{times(T)\}F(x)=max{times(T)},满足 TTT 是 SSS 的子串且 ∣T∣=x|T|=x∣T∣=x。例如当 S=ababaS=ababaS=ababa 时 F(3)=2F(3)=2F(3)=2 ,因为 SSS 中有一个出现 222 次的子串 abaabaaba。 你的任务是对于每个 1≤i≤∣S∣1\le i \le |S|1≤i≤∣S∣ 输出 F(i)F(i)F(i)。
题目描述
You are given a string S which consists of 250000 lowercase latin letters at most. We define F(x) as the maximal number of times that some string with length x appears in S. For example for string ‘ababa’ F(3) will be 2 because there is a string ‘aba’ that occurs twice. Your task is to output F(i) for every i so that 1<=i<=|S|.
输入格式
String S consists of at most 250000 lowercase latin letters.
输出格式
Output |S| lines. On the i-th line output F(i).
样例 #1
样例输入 #1
ababa
样例输出 #1
3
2
2
1
1
题意:
给一个字符串S,令F(x)表示S的所有长度为x的子串中,出现次数的最大值。求F(1)…F(Length(S))
思路:
构建 s 的 SAM,对于每个 SAM 状态 u 能表示的子串长度范围是 [ len[fa(u)] + 1, len[s] ],这些子串的出现次数等价于 cnt[u]。
那么问题变成用 cnt[u] 去区间更新 [ len[fa(u)] + 1, len[u] ] 的最大值。(无脑线段树?SPOJ 时限仅 100 ms,喜提TLE。怎么优化呢?)
我们发现 f[i] 是非严格单调递减的,我们 只用 cnt[u] 去更新 f[len[u]], 然后使用推标记的方法,从后向前令 f[i] = max(f[i], f[i + 1]) 即可。
代码:
#include<bits/stdc++.h>using namespace std;const int N = 2.5e5 + 10, M = N << 1;
int ch[M][26], len[M], fa[M], np = 1, tot = 1;
long long cnt[M], f[N];
vector<int> g[M];
char s[N];void extend(int c)
{int p = np; np = ++tot;len[np] = len[p] + 1, cnt[np] = 1;while (p && !ch[p][c]) {ch[p][c] = np;p = fa[p];}if (!p) {fa[np] = 1;}else {int q = ch[p][c];if (len[q] == len[p] + 1) {fa[np] = q;}else {int nq = ++tot;len[nq] = len[p] + 1;fa[nq] = fa[q], fa[q] = fa[np] = nq;while (p && ch[p][c] == q) {ch[p][c] = nq;p = fa[p];}memcpy(ch[nq], ch[q], sizeof ch[q]);}}
}void dfs(int u)
{for (auto son : g[u]) {dfs(son);cnt[u] += cnt[son];}int l = len[fa[u]] + 1, r = len[u];f[r] = max(1ll * f[r], 1ll * cnt[u]);
}signed main()
{scanf("%s", s);int n = strlen(s);for (int i = 0; s[i]; ++i) {extend(s[i] - 'a');}for (int i = 2; i <= tot; ++i) {g[fa[i]].emplace_back(i);}dfs(1);for (int i = n - 1; i >= 1; --i) {f[i] = max(f[i], f[i + 1]);}for (int i = 1; i <= n; ++i) {printf("%lld\n", f[i]);}return 0;
}
相关文章:
)
SPOJ-NSUBSTR - Substrings(SAM求所有长度子串的最大出现次数)
NSUBSTR - Substrings 题面翻译 你得到了一个最多由 250000250000250000 个小写拉丁字母组成的字符串 SSS。定义 F(x)F(x)F(x) 为 SSS 的某些长度为 xxx 的子串在 SSS 中的最大出现次数。即 F(x)max{times(T)}F(x)max\{times(T)\}F(x)max{times(T)},满足 TTT 是 S…...
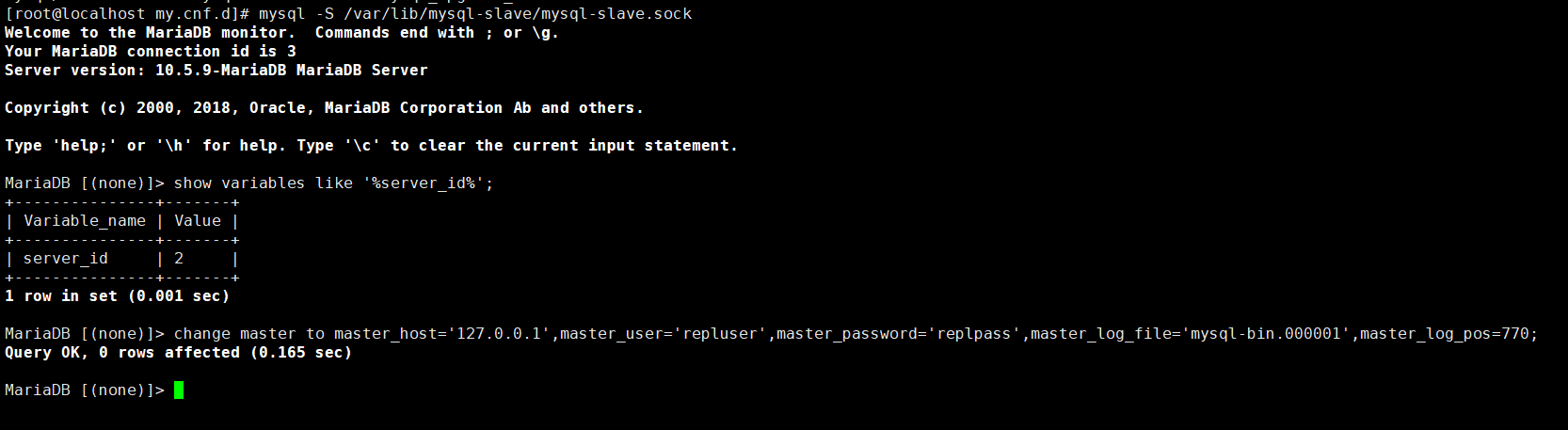
Mariadb10.5基于同服务器多实例主从配置
本次部署环境:Centos8stream 本次部署mariadb版本: mariadb:10.5 本次部署方式:rpm包直接安装,并通过systemd直接托管 可以参考 /usr/lib/systemd/system/mariadb.service 该文件 # Multi instance version of mariadb. For i…...

linux 修改主机名称
1、hostname命令进行临时更改 如果只需要临时更改主机名,可以使用hostname命令: sudo hostname <new-hostname> 例如: 只需重新打开session终端,就能生效, 但是,重启计算机后会回到旧的主机名。…...
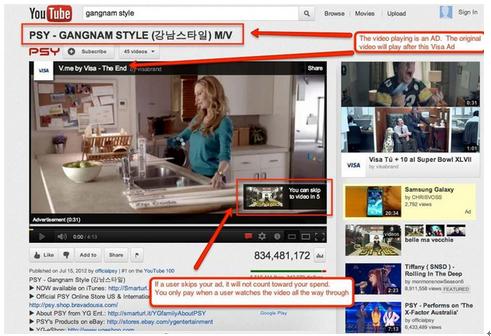
学校的地下网站(学校的地下网站1080P高清)
这个问题本身就提得有问题,为什么这么说,这是因为YouTube本身就不是一个视频网站或者说YouTube不是一个传统的视频网站!!! YouTube能够一家独大,可不仅仅是因为有了Google 这个亲爹,还有一点&am…...

勒索病毒是什么?如何防勒索病毒
勒索病毒并不是某一个病毒,而是一类病毒的统称,主要以邮件、程序、木马、网页挂马的形式进行传播,利用各种加密算法对文件进行加密,被感染者一般无法解密,必须拿到解密的私钥才有可能破解。 已知最早的勒索软件出现于 …...

SpringBoot+VUE+Axios 【链接超时】 后端正常返回结果,前端却出现错误无法接收数据
一、错误原因及解决思路 错误提示表明前端发送的请求在默认的 2500ms 超时时间内没有得到服务器的响应,导致请求失败。尝试以下方法来解决这个问题: 增加请求超时时间:可以通过配置 Axios 请求对象的 timeout 属性来增加请求的超时时间&…...
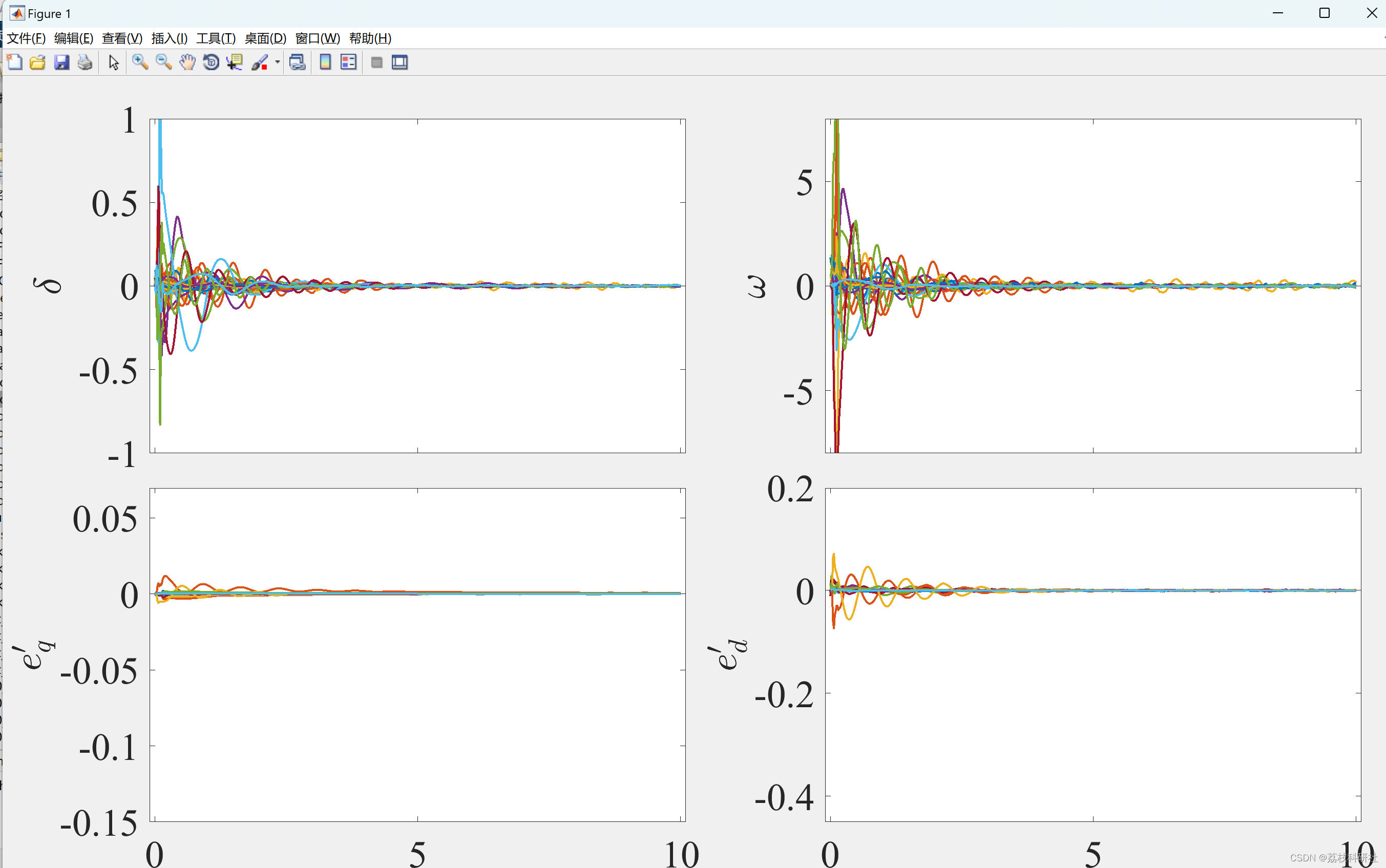
【状态估计】基于增强数值稳定性的无迹卡尔曼滤波多机电力系统动态状态估计(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

快速排序的简单理解
详细描述 快速排序通过一趟排序将待排序列分割成独立的两部分,其中一部分序列的关键字均比另一部分序列的关键字小,则可分别对这两部分序列继续进行排序,以达到整个序列有序的目的。 快速排序详细的执行步骤如下: 从序列中挑出…...
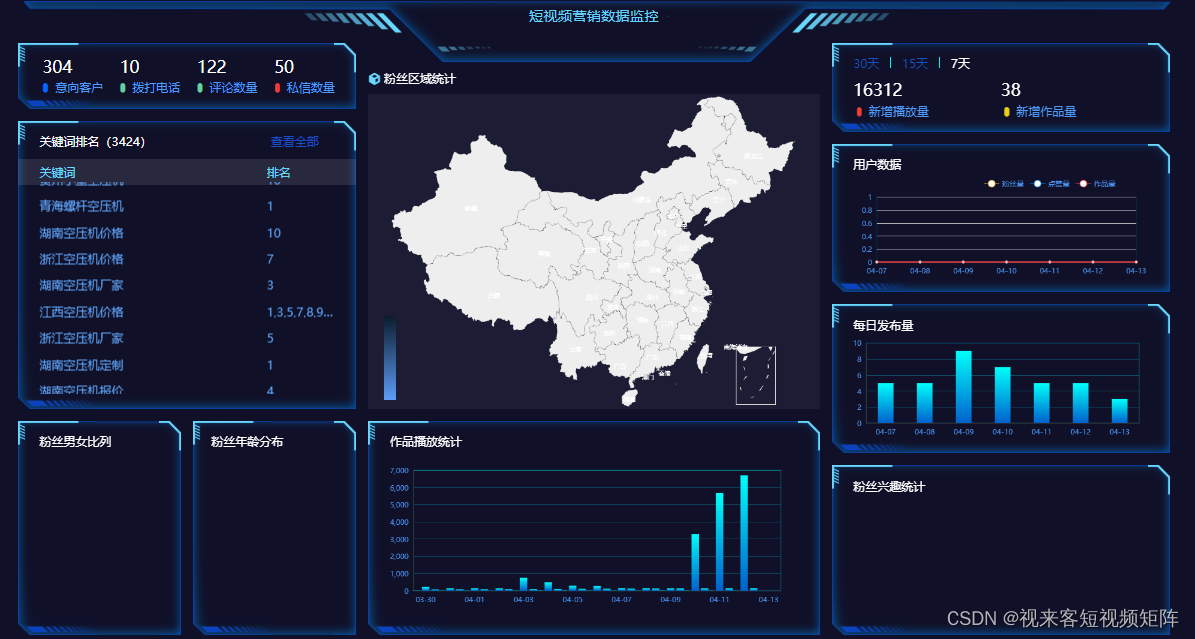
短视频多平台发布软件功能详解
随着移动互联网的普及和短视频的兴起,短视频发布软件越来越受到人们的关注。短视频发布软件除了常规的短视频发布功能,还拥有智能创作、帐号绑定、短视频一键发布、视频任务管理和数据统计等一系列实用功能。下面我们将分步骤详细介绍一下这些功能。 …...

谷歌人机验证Google reCAPTCHA
reCAPTCHA是Google公司推出的一项验证服务,使用十分方便快捷,在国外许多网站上均有使用。它与许多其他的人机验证方式不同,它极少需要用户进行各种识图验证。 它的使用方式如下如所示,只需勾选复选框即可通过人机验证。 虽然简单…...
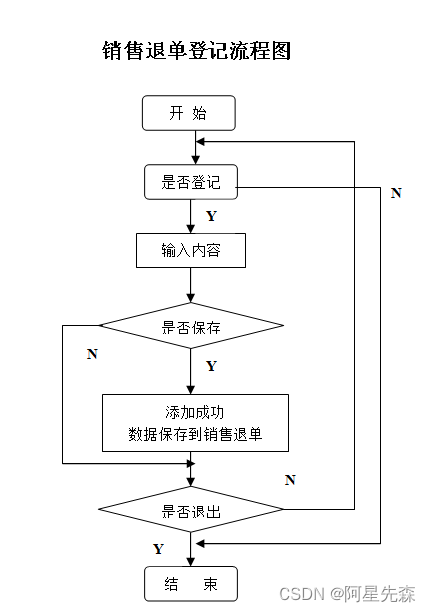
VB+ACCESS电脑销售系统的设计与实现
为了使此系统简单易学易用、功能强大、软件费用支出低、见效快等特点,我们选择Visual Basic6.0开发此系统。Visual Basic6.0起代码有效率以达到Visual c的水平。在面向对象程序设计方面,Visual Basic6.0全面支持面向对你程序设计包括数据抽象、封装、对象…...

嵌入式开发:硬件和软件越来越接近
从前,硬件和软件工程师大多生活在自己的世界里。硬件团队设计了芯片,调试了从铸造厂返回的第一批样本,让软件团队测试他们的代码。随着虚拟平台和其他可执行模型变得越来越普遍,软件团队可以在芯片制造之前开始,有时甚…...
亲测:腾讯云轻量应用服务器性能如何?
腾讯云轻量应用服务器性能评测,轻量服务器CPU主频、处理器型号、公网带宽、月流量、Ping值测速、磁盘IO读写及使用限制,轻量应用服务器CPU内存性能和标准型云服务器CVM处于同一水准,所以大家不要担心轻量应用服务器的性能,腾讯云百…...
编程语言,TIOBE 4 月榜单:黑马出现了
TIOBE 4 月榜单已经发布了,一起来看看这个月编程语言排行榜有什么变化吧! C 发展依旧迅猛 在本月榜单中,TOP 20 的变动不大,Python、C、Java 、 C 和C#依然占据前五。甚至排名顺序都和上个月一样没有变动。 同时,Rus…...

基于DSP+FPGA的机载雷达伺服控制系统(二)电源仿真
板级电源分配网络的分析与仿真在硬件电路设计中,电源系统的设计是关键步骤之一,良好的电源系统为电路板 上各种信号的传输提供了保障。本章将研究电源完整性的相关问题,并提出一系列改 进电源质量的措施。 3.1 电源完整性 电源完整性…...

SpringBoot整合Redis、以及缓存穿透、缓存雪崩、缓存击穿的理解分布式情况下如何添加分布式锁 【续篇】
文章目录前言1、分布式情况下如何加锁2、具体实现过程3、测试3.1 一个服务按照多个端口同时启动3.2 使用jmeter进行压测前言 上一篇实现了单体应用下如何上锁,这一篇主要说明如何在分布式场景下上锁 上一篇地址:加锁 1、分布式情况下如何加锁 需要注意的点是: 在上锁和释放…...

优漫动游告诉你:平面设计适合你吗?
优漫动游告诉你:平面设计适合你吗? 什么样的同学可以适应平面设计这份工作呢? 略微有美术基础,当然功底越深越加分。 2.对色彩、形状、结构有一定的接纳力。 3.对图案、人像、字体等因素有审美辨别的能力…...

在Vue中,为什么从 props 中解构变量之后再watch它,无法检测到它的变化?
例如下面这段代码,msg无法被watch import { watch } from vue;export default {props: {msg: String},setup(props) {// 从 props 中解构 msgconst { msg } props;watch(() > msg,(newVal, oldVal) > {console.log(newVal, newVal);console.log(oldVal, old…...

[源码解析]socket系统调用上
文章目录socket函数API内核源码sock_createinet_createsock_allocsock_map_fd相关数据结构本文将以socket函数为例,分析它在Linux5.12.10内核中的实现,先观此图,宏观上把握它在内核中的函数调用关系:socket函数API socket 函数原…...

Jenkins部署与自动化构建
Jenkins笔记 文章目录Jenkins笔记[toc]一、安装Jenkinsdocker 安装 JenkinsJava启动war包直接安装二、配置mavenGit自动构建jar包三、自动化发布到测试服务器运行超时机制数据流重定向编写清理Shell脚本四、构建触发器1. 生成API token2. Jenkins项目配置触发器3. 远程Git仓库配…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
