当前位置： 首页 > news >正文

python学习，全球有哪些特别好的社区推荐呢？

news 2026/2/11 2:09:48

Surfshark可以访问全球社区学习的surfshark工具使用方法教程：qptool.net/shark.html

 

以下是一些全球范围内比较受欢迎的 Python 学习社区：

中文社区：csdn.net

优势：本土国语社区，获得相关知识与经验便利。

Python官方社区：www.python.org/community

优势：由 Python 官方运营，可以获得官方的指导和解答；社区成员水平较高。

劣势：有时官方解答可能过于简单，缺少深度讨论。

Stack Overflow：stackoverflow.com

优势：庞大的社区，几乎所有的问题都可以在这里找到解答；质量较高的答案，有专业人士进行解答。

劣势：有时会有重复或不够详细的答案；如果问题太过基础或过于简单，可能会被网友质疑。

GitHub：github.com

优势：全球最大的代码托管网站之一，可以从中学习优秀的代码实现；提供了大量的开源项目供学习。

劣势：难度较高，需要一定的编程基础。

Reddit上的Python社区：www.reddit.com/r/Python

优势：内容种类繁多，社区用户较为活跃；可以上载和下载 Python 项目。

劣势：讨论有时不太深入，回答质量参差不齐。

 

PyPI（Python Package Index）：pypi.org

 

Kaggle：www.kaggle.com

 

DataCamp社区：www.datacamp.com/community

 

Real Python：realpython.com

 

Python Weekly：www.pythonweekly.com

 

Python-forum.io：www.python-forum.io

以上这些社区都是非常活跃的，有许多专业的 Python 开发者和爱好者，都是一群热爱分享的朋友，可以帮助你解决各种问题，分享经验，了解最新的 Python 技术和趋势。如果你对Python有兴趣，而且语言过关，这些社区一定不要错过，可以帮助你快速成长哦。

 

相关文章：

python学习，全球有哪些特别好的社区推荐呢？

Surfshark可以访问全球社区学习的surfshark工具使用方法教程：qptool.net/shark.html 以下是一些全球范围内比较受欢迎的 Python 学习社区： 中文社区：csdn.net 优势：本土国语社区，获得相关知识与经验便利。 Python官…...

编程日记 2023/4/15 23:53:26

LC-1042. 不邻接植花（四色问题(染色法)）

1042. 不邻接植花 难度中等198 有 n 个花园，按从 1 到 n 标记。另有数组 paths ，其中 paths[i] [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中，你打算种下四种花之一。 另外，所有花园 最多 有 3 条路径可以进入…...

编程日记 2023/4/15 23:48:25

python实战应用讲解-【numpy科学计算】scikits-learn模块（附python示例代码）

目录 Numpy 安装scikits-learn 准备工作 具体步骤 Numpy 加载范例数据集 具体步骤...

编程日记 2023/4/15 23:43:24

大数据开发必备面试题Spark篇01

1、Hadoop 和 Spark 的相同点和不同点？ Hadoop 底层使用 MapReduce 计算架构，只有 map 和 reduce 两种操作，表达能力比较欠缺，而且在 MR 过程中会重复的读写 hdfs，造成大量的磁盘 io 读写操作，所以适合高时…...

编程日记 2023/4/15 23:38:23

SpringBoot整合xxl-job详细教程

SrpingBoot整合xxl-job，实现任务调度说明调度中心执行器调试整合SpringBoot说明 Xxl-Job是一个轻量级分布式任务调度平台，其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线，开箱即用。Xxl-Job有…...

编程日记 2023/4/15 23:33:22

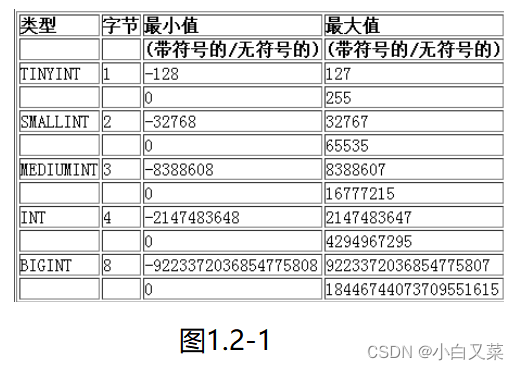
【MySQL--04】数据类型

文章目录1.数据类型1.1数据类型分类1.2数值类型1.2.1tinyint类型1.2.2bit类型1.2.3小数类型1.2.3.1 float1.2.3.2 decimal1.3字符串类型1.3.1 char1.3.2 varchar1.3.3char和varchar的比较1.4日期和时间类型1.5 enum和set1.5.1 enum1.5.2 set1.5.3 示例1.数据类型 1.1数据类型分…...

编程日记 2023/6/1 13:06:39

git 将其它分支的文件检出到工作区

主要是使用如下命令&#xff1a; git checkout [-f|--ours|--theirs|-m|--conflict<style>] [<tree-ish>] [--] <pathspec>…​覆盖与 pathspec 匹配的文件的内容。当没有给出<tree-ish> (通常是一个commit)时&#xff0c;用 index 中的内容覆盖工作树…...

编程日记 2023/4/15 23:23:19

人工智能的最大危险是什么？

作者&#xff1a;GPT(AI智学习) 链接&#xff1a;https://www.zhihu.com/question/592107303/answer/2966857095 来源&#xff1a;知乎 著作权归作者所有。商业转载请联系作者获得授权&#xff0c;非商业转载请注明出处。 首先&#xff1a;人工智能为人类带来了很多益处&…...

编程日记 2023/4/15 23:18:18

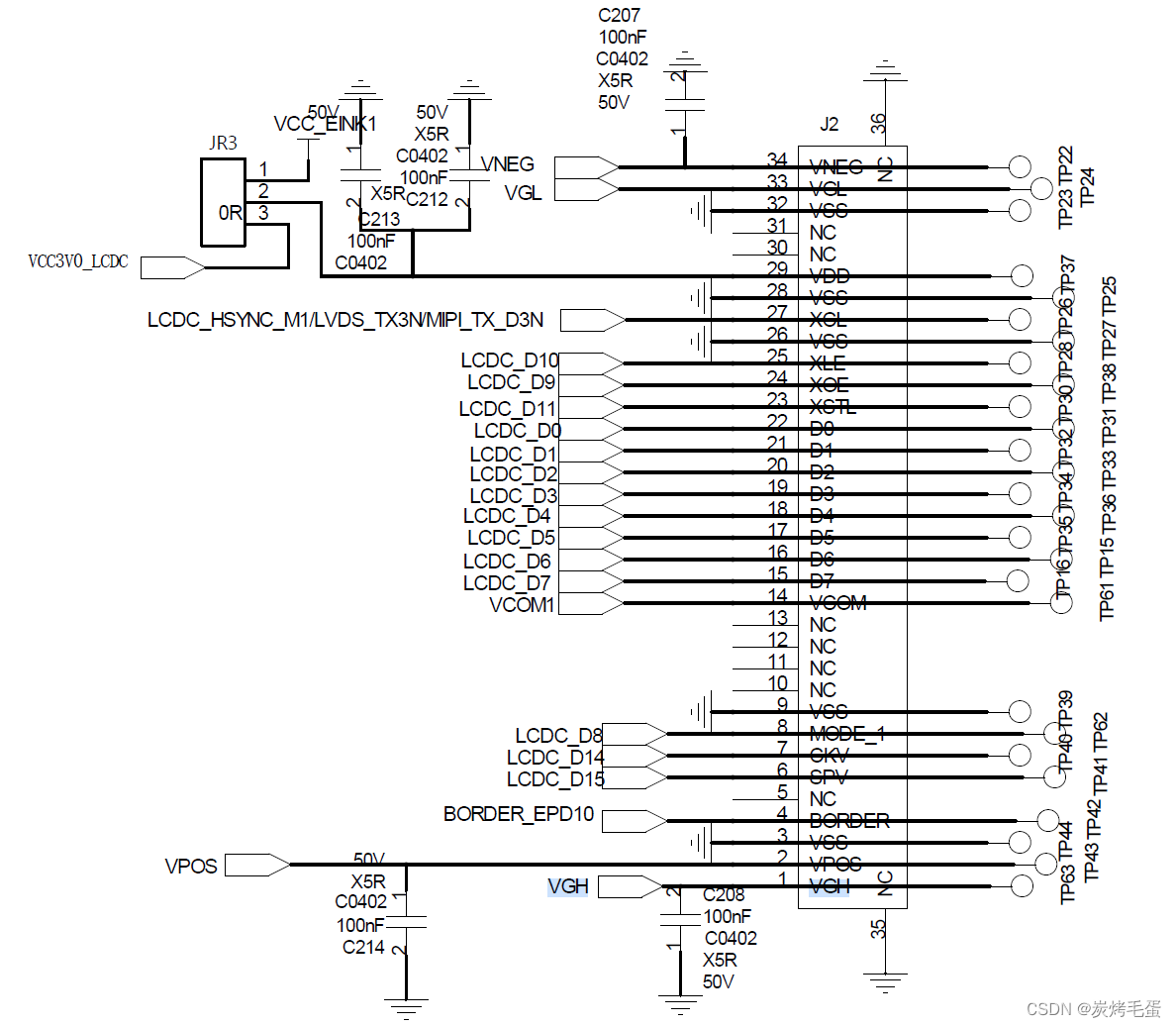
rk3568点亮E-ink

rk3568 Android11/12 适配 E-ink “EINK”是英语ElectronicInk的缩写。翻译成中文为“电子墨水”。电子墨水由数百万个微胶囊(Microcapsules)所构成&#xff0c;微胶囊的大小约等同于人类头发的直径。每个微胶囊里含有电泳粒子──带负电荷的白色以及带正电荷的黑色粒子&#…...

编程日记 2023/4/15 23:13:18

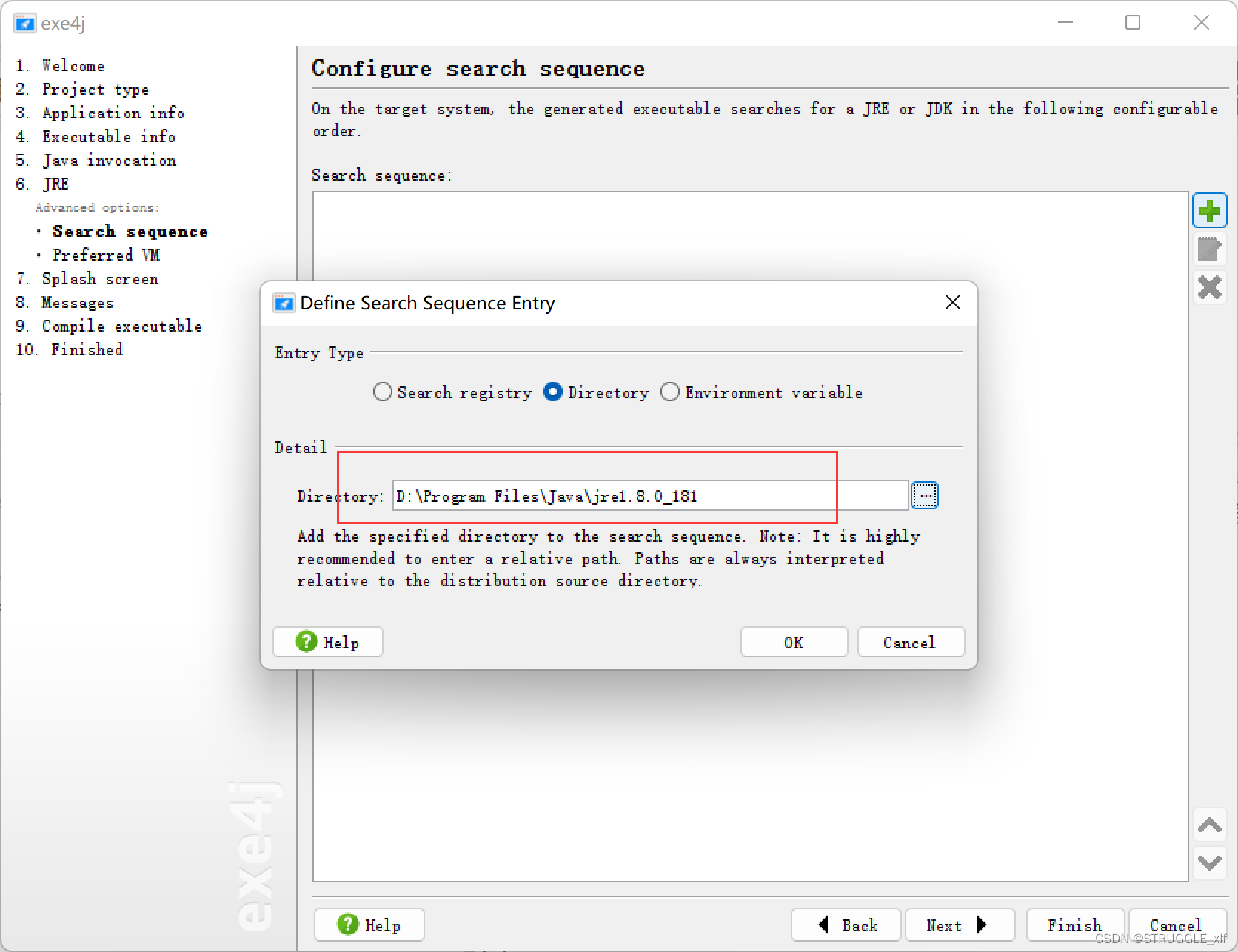
如何将Springboot项目通过IDEA打包成jar包，并且转换成可执行文件

首先在IDEA打开你的项目&#xff0c;需要确认项目可以正常运行&#xff0c;然后点击页面右侧的Maven,运行Lifecycle下的package, 此时在项目的target目录下就可以看到一个jar包 这个时候你可以在jar包所在目录下执行cmd窗口&#xff0c;运行 java -jar campus-market-0.0.1-S…...

编程日记 2023/4/15 23:08:16

总结：网卡

一、背景 经常听到eth0&#xff0c;bond0这些概念&#xff0c;好奇他们的区别&#xff0c;于是有了此篇文章记录下。 二、介绍 网卡&#xff1a;即网络接口板&#xff0c;又称网络适配器或NIC (网络接口控制器)&#xff0c;是一块被设计用来允许计算机在计算机网络上进行通讯…...

编程日记 2023/5/30 6:56:59

Java这么卷，还有前景吗？

“Java很卷”、“大家不要再卷Java了”&#xff0c;经常听到同学这样抱怨。但同时&#xff0c;Java的高薪也在吸引越来越多的同学。不少同学开始疑惑&#xff1a;既然Java这么卷&#xff0c;还值得我入行吗&#xff1f; 首先先给你吃一颗定心丸&#xff1a;现在选择Java依然有…...

编程日记 2023/5/31 3:43:26

后端简易定时任务框架选择(Python/Go)--gocron

文章目录前言实现后语前言 在使用Python的web框架中&#xff0c;包括flask/Django&#xff0c;其中大量用到celery&#xff1b;celery作为异步任务使用的多&#xff0c;同时也会用celery来跑些定时任务&#xff0c;比如每晚定时跑脚本、跑数据统计等闲时任务。但随着任务量的增…...

编程日记 2023/4/15 22:53:12

【GStreamer学习】之GStreamer基础教程

目标 没有什么比在屏幕上打印出“Hello World”更能获得对软件库的第一印象了&#xff01; 但是由于我们正在学习多媒体框架&#xff0c;所以我们将输出“Hello World&#xff01;”改为播放视频。 不要被下面的代码量吓到&#xff1a;只有 4 行是真正需要的&#xff0c; 其…...

编程日记 2023/4/15 22:48:11

各类Round-Robin总结，含Verilog实现

1. Fixed Priority Arbitrary 固定优先级就是指每个req的优先级是不变的，即优先级高的先被处理，优先级低的必须是在没有更高优先级的req的时候才会被处理。所以转化为数学模型就是找出req序列中第一个为1的位置，然后将其转换为onehot。 例如： req[3:0] = 4b1100 ==> g…...

编程日记 2023/4/15 22:43:10

《软件设计师-知识点》

1、指令流水线 &#xff08;一&#xff09;一条指令的执行过程可分为三个阶段&#xff1a;取指、分析、执行。 取指&#xff1a;根据PC&#xff08;程序计数器&#xff09;内容访问主存储器&#xff0c;取出一条指令送到IR&#xff08;指令寄存器&#xff09;中。 分析&…...

编程日记 2023/4/15 22:38:09

mysql 同义词_数据库中的同义词synonym

一、Oracle数据只有一个实例(简单理解就是Oracle 只能建立一个数据库&#xff0c;不像MySQL&#xff0c;它下面可以创建N个库)&#xff0c;那么Oracle是根据用户灵活去管理的&#xff1b;这点读起来、理解 起来也不那么难&#xff0c;但是除非自己亲自实现一把才理解深入点&…...

编程日记 2023/6/1 13:08:21

Nacos共享配置

本文介绍一下Nacos作为配置中心时&#xff0c;如何读取共享配置 我的环境 Windows10JDK8SpringCloud&#xff1a;Finchley.RELEASESpringBoot&#xff1a;2.0.4.RELEASEspring-cloud-alibaba-dependencies&#xff1a;0.2.2.RELEASENacos-server&#xff1a;1.0.1 本文的项目…...

编程日记 2023/4/15 22:28:06

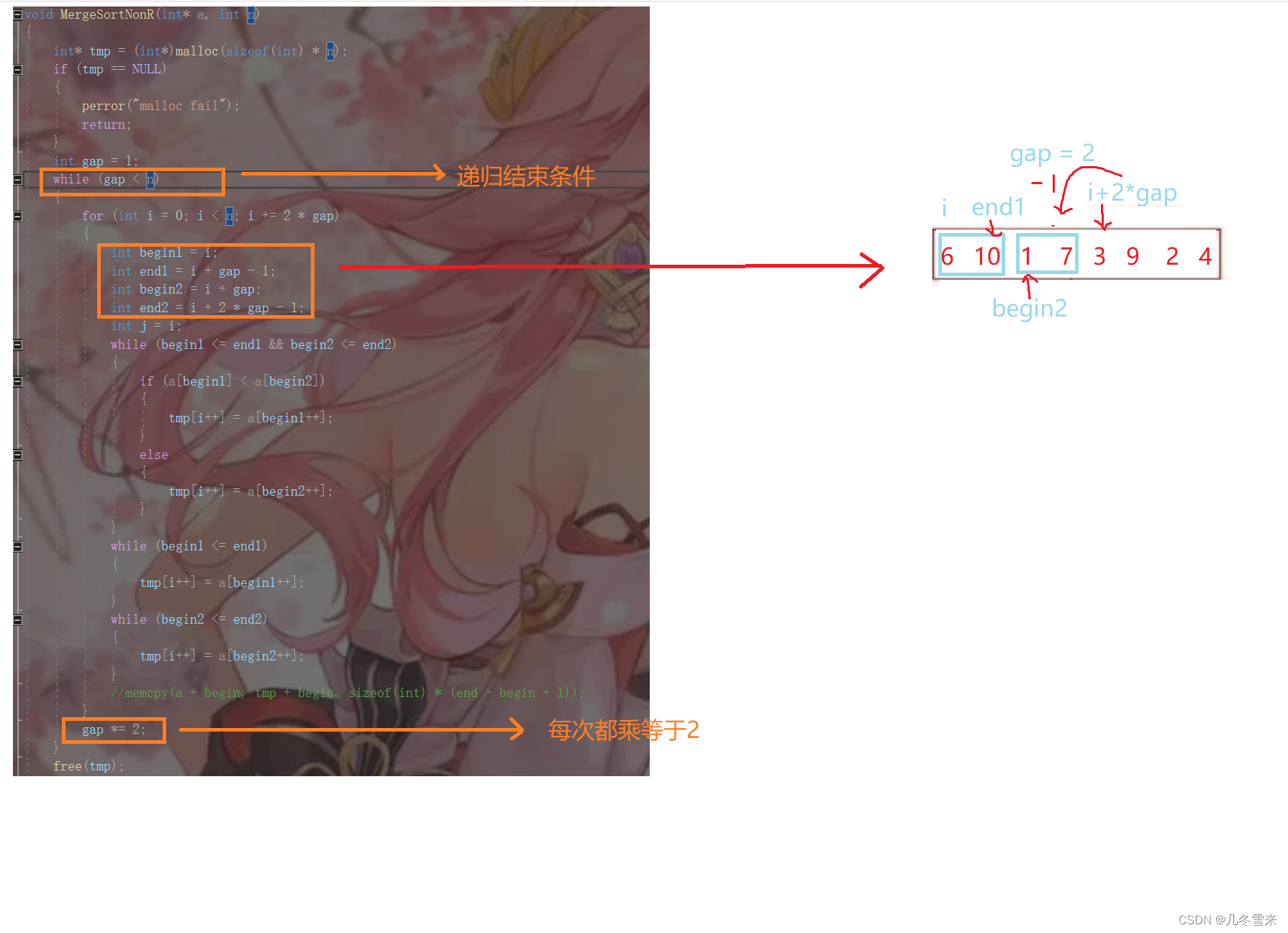
数据结构——排序（4）

作者&#xff1a;几冬雪来 时间&#xff1a;2023年4月12日 内容&#xff1a;数据结构排序内容讲解 目录 前言&#xff1a; 1.快速排序中的递归&#xff1a; 2.小区间优化&#xff1a; 3.递归改非递归&#xff1a; 4.归并排序&#xff1a; 5.归并排序的非递归形式&…...

编程日记 2023/4/15 22:23:05

C++13:搜索二叉树

目录 搜索二叉树概念 模拟实现搜索二叉树 插入函数实现 插入函数实现&#xff08;递归&#xff09; 查找函数实现 删除函数实现 删除函数实现&#xff08;递归&#xff09; 中序遍历实现 拷贝构造函数实现 析构函数实现 赋值重载 我们在最开始学习二叉树的时候&#xff0c;…...

编程日记 2023/6/1 5:55:17

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录

ASP.NET Core 是一个跨平台的开源框架&#xff0c;用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录&#xff0c;以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

编程新知 2026/2/8 4:37:06

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

从WWDC看苹果产品发展的规律

WWDC 是苹果公司一年一度面向全球开发者的盛会&#xff0c;其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具&#xff0c;对过去十年 WWDC 主题演讲内容进行了系统化分析&#xff0c;形成了这份…...

编程新知 2026/2/2 21:52:33

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？

Otsu 是一种自动阈值化方法&#xff0c;用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理&#xff0c;能够自动确定一个阈值&#xff0c;将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

编程新知 2026/1/9 19:36:58

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/12/13 4:20:30

Python ROS2【机器人中间件框架】 简介

销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

编程新知 2026/1/29 9:12:46

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

算法岗面试经验分享-大模型篇

文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer &#xff08;1&#xff09;资源 论文&a…...

编程新知 2026/1/23 11:58:06

短视频矩阵系统文案创作功能开发实践，定制化开发

在短视频行业迅猛发展的当下&#xff0c;企业和个人创作者为了扩大影响力、提升传播效果&#xff0c;纷纷采用短视频矩阵运营策略&#xff0c;同时管理多个平台、多个账号的内容发布。然而&#xff0c;频繁的文案创作需求让运营者疲于应对&#xff0c;如何高效产出高质量文案成…...

编程新知 2026/2/1 8:24:29