[Eigen中文文档] Array类与元素操作
文档总目录
本文目录
- 什么是Array类?
- Array类型
- 访问Array中的值
- 加法与减法
- Array乘法
- 其他按元素操作的运算
- array和matrix表达式之间的转换
英文原文(The Array class and coefficient-wise operations)
本页旨在提供有关如何使用Eigen的Array类的概述和说明。
什么是Array类?
与Matrix类用于线性代数计算不同的是,Array类提供了通用目的数组。此外,Array类提供了一种执行按系数运算的简单方法,这可能没有线性代数意义,例如对每一个元素都加一个常数或按系数将两个数组相乘。
Array类型
Array是一个类模板,采用与Matrix相同的模板参数。与Matrix一样,前三个模板参数是必需的:
Array<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>
最后三个模板参数是可选的。由于这与Matrix完全相同,因此不再在此解释,仅参考Matrix 类。
Eigen还提供了一些常见的类型定义,其方式类似于Matrix类型定义,但有一些细微差别,因为Array一词用于一维和二维数组。使用ArrayNt代表一维N个大小的标量,其中 N 和 t 是大小和标量类型,详见[矩阵与向量运算](# 3.1.2 矩阵与向量运算)。对于二维数组类型,使用 ArrayNNt 表示。示例如下:
| 类型 | 类型定义 |
|---|---|
| Array<float,Dynamic,1> | ArrayXf |
| Array<float,3,1> | Array3f |
| Array<double,Dynamic,Dynamic> | ArrayXXd |
| Array<double,3,3> | Array33d |
访问Array中的值
就像矩阵一样,使用括号运算符可以访问数组中的值。另外,<<运算符可用于初始化数组(使用逗号初始化)或打印它们。
例如:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::ArrayXXf m(2,2);// assign some values coefficient by coefficientm(0,0) = 1.0; m(0,1) = 2.0;m(1,0) = 3.0; m(1,1) = m(0,1) + m(1,0);// print values to standard outputstd::cout << m << std::endl << std::endl;// using the comma-initializer is also allowedm << 1.0,2.0,3.0,4.0;// print values to standard outputstd::cout << m << std::endl;
}
输出如下:
1 2
3 51 2
3 4
有关逗号初始化的更多信息,请参阅高级初始化。
加法与减法
两个数组的加减法与矩阵相同。如果两个数组的大小相同,并且加法或减法是按系数进行的,则该操作有效。
Array 还支持 array + scalar 的表达形式,这实现了对数组的每个系数都加一个常数。并且这是在Matrix类中不能直接使用的功能。
示例如下:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::ArrayXXf a(3,3);Eigen::ArrayXXf b(3,3);a << 1,2,3,4,5,6,7,8,9;b << 1,2,3,1,2,3,1,2,3;// Adding two arraysstd::cout << "a + b = " << std::endl << a + b << std::endl << std::endl;// Subtracting a scalar from an arraystd::cout << "a - 2 = " << std::endl << a - 2 << std::endl;
}
输出如下:
a + b = 2 4 65 7 98 10 12a - 2 =
-1 0 12 3 45 6 7
Array乘法
当然你可以将一个数组乘以一个标量,这与矩阵相同。数组与矩阵不同的地方在于自身相乘,矩阵将乘法解释为矩阵乘积,而数组将乘法解释为系数乘积。因此,两个数组相乘时它们必须具有相同的维度。
示例如下:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::ArrayXXf a(2,2);Eigen::ArrayXXf b(2,2);a << 1,2,3,4;b << 5,6,7,8;std::cout << "a * b = " << std::endl << a * b << std::endl;
}
输出如下:
a * b = 5 12
21 32
其他按元素操作的运算
除了上述的加法、减法和乘法运算符之外,Array 类还定义了其他按系数计算的运算。例如,abs() 方法对每个元素取绝对值,而sqrt()计算每个系数的平方根。如果你有两个相同大小的数组,你可以调用min(.)来构造一个数组,其元素是两个给定数组对应元素的最小值。这些操作在以下示例中进行了说明:
#include <Eigen/Dense>
#include <iostream>int main()
{Eigen::ArrayXf a = Eigen::ArrayXf::Random(5);a *= 2;std::cout << "a =" << std::endl<< a << std::endl;std::cout << "a.abs() =" << std::endl<< a.abs() << std::endl;std::cout << "a.abs().sqrt() =" << std::endl<< a.abs().sqrt() << std::endl;std::cout << "a.min(a.abs().sqrt()) =" << std::endl<< a.min(a.abs().sqrt()) << std::endl;
}
输出如下:
a =1.36
-0.4221.131.191.65
a.abs() =1.36
0.4221.131.191.65
a.abs().sqrt() =
1.17
0.65
1.06
1.09
1.28
a.min(a.abs().sqrt()) =1.17
-0.4221.061.091.28
array和matrix表达式之间的转换
什么时候应该使用Matrix 类的对象,什么时候应该使用 Array 类的对象呢?
首先, Matrix 类和Array类的方法不通用。如果需要进行线性代数运算,例如矩阵乘法,那么应该使用 Matrix 类;如果需要做元素运算,那么应该使用Array类。然而,有时并没有那么简单,而是需要同时使用Matrix 类和Array类。这种情况下,需要将Matrix 转换为Array或相反。这样就可以使用所有操作,而不管对象声明为Matrix 还是Array。
Matrix 类有一个 .array() 方法可以将Matrix 转换为Array。同样,Array有一个 .matrix() 方法。由于Eigen表达式的抽象,这些转换发生在编译的时候,所以不需要任何运行时间成本。.array()和.matrix()既可以作为左值,也可以作为右值。
Eigen 禁止在表达式中混合使用Matrix 和Array。例如,不能将Matrix 和Array直接相加;运算符的操作对象要么都是Matrix,要么都是Array,但转换后是可以的。此规则的例外是赋值运算符,允许将Matrix 赋值给Array,或将将 Array 赋值给Matrix。
以下示例展示了如何通过使用.array()方法对 Matrix 对象使用Array的方法。例如,语句 result = m.array() * n.array() 将两个矩阵m和n都转换为数组,并使它们按系数相乘,再将结果分配给矩阵变量(这是合法的,因为Eigen允许将数组表达式赋值给矩阵变量)。
事实上,这种用例非常普遍,以至于Eigen为矩阵提供了一个 const .cwiseProduct(.) 方法来满足按元素相乘的需求。
示例如下:
#include <Eigen/Dense>
#include <iostream>using Eigen::MatrixXf;int main()
{MatrixXf m(2,2);MatrixXf n(2,2);MatrixXf result(2,2);m << 1,2,3,4;n << 5,6,7,8;result = m * n;std::cout << "-- Matrix m*n: --\n" << result << "\n\n";result = m.array() * n.array();std::cout << "-- Array m*n: --\n" << result << "\n\n";result = m.cwiseProduct(n);std::cout << "-- With cwiseProduct: --\n" << result << "\n\n";result = m.array() + 4;std::cout << "-- Array m + 4: --\n" << result << "\n\n";
}
输出如下:
-- Matrix m*n: --
19 22
43 50-- Array m*n: --5 12
21 32-- With cwiseProduct: --5 12
21 32-- Array m + 4: --
5 6
7 8
同样,如果array1和array2是数组,则表达式array1.matrix() * array2.matrix()可以计算他们的矩阵乘积。
接下来是一个更复杂一点的示例,表达式(m.array() + 4).matrix() * m对每一个元素都加4,然后计算表达式结果与矩阵m的矩阵乘积。类似的,表达式(m.array() * n.array()).matrix() * m按元素计算矩阵m和n的乘积,然后计算其结果与m的矩阵乘法。
示例如下:
#include <Eigen/Dense>
#include <iostream>using Eigen::MatrixXf;int main()
{MatrixXf m(2,2);MatrixXf n(2,2);MatrixXf result(2,2);m << 1,2,3,4;n << 5,6,7,8;result = (m.array() + 4).matrix() * m;std::cout << "-- Combination 1: --\n" << result << "\n\n";result = (m.array() * n.array()).matrix() * m;std::cout << "-- Combination 2: --\n" << result << "\n\n";
}
输出如下:
-- Combination 1: --
23 34
31 46-- Combination 2: --41 58
117 170
相关文章:

[Eigen中文文档] Array类与元素操作
文档总目录 本文目录什么是Array类?Array类型访问Array中的值加法与减法Array乘法其他按元素操作的运算array和matrix表达式之间的转换英文原文(The Array class and coefficient-wise operations) 本页旨在提供有关如何使用Eigen的Array类的概述和说明。 什么是A…...

python学习,全球有哪些特别好的社区推荐呢?
Surfshark可以访问全球社区学习的surfshark工具使用方法教程:qptool.net/shark.html 以下是一些全球范围内比较受欢迎的 Python 学习社区: 中文社区:csdn.net 优势:本土国语社区,获得相关知识与经验便利。 Python官…...
))
LC-1042. 不邻接植花(四色问题(染色法))
1042. 不邻接植花 难度中等198 有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。 另外,所有花园 最多 有 3 条路径可以进入…...
)
python实战应用讲解-【numpy科学计算】scikits-learn模块(附python示例代码)
目录 Numpy 安装scikits-learn 准备工作 具体步骤 Numpy 加载范例数据集 具体步骤...

大数据开发必备面试题Spark篇01
1、Hadoop 和 Spark 的相同点和不同点? Hadoop 底层使用 MapReduce 计算架构,只有 map 和 reduce 两种操作,表达能力比较欠缺,而且在 MR 过程中会重复的读写 hdfs,造成大量的磁盘 io 读写操作,所以适合高时…...
SpringBoot整合xxl-job详细教程
SrpingBoot整合xxl-job,实现任务调度说明调度中心执行器调试整合SpringBoot说明 Xxl-Job是一个轻量级分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线,开箱即用。Xxl-Job有…...
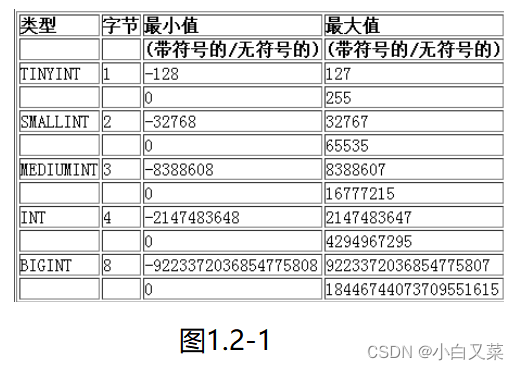
【MySQL--04】数据类型
文章目录1.数据类型1.1数据类型分类1.2数值类型1.2.1tinyint类型1.2.2bit类型1.2.3小数类型1.2.3.1 float1.2.3.2 decimal1.3字符串类型1.3.1 char1.3.2 varchar1.3.3char和varchar的比较1.4日期和时间类型1.5 enum和set1.5.1 enum1.5.2 set1.5.3 示例1.数据类型 1.1数据类型分…...

git 将其它分支的文件检出到工作区
主要是使用如下命令: git checkout [-f|--ours|--theirs|-m|--conflict<style>] [<tree-ish>] [--] <pathspec>…覆盖与 pathspec 匹配的文件的内容。当没有给出<tree-ish> (通常是一个commit)时,用 index 中的内容覆盖工作树…...

人工智能的最大危险是什么?
作者:GPT(AI智学习) 链接:https://www.zhihu.com/question/592107303/answer/2966857095 来源:知乎 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 首先:人工智能为人类带来了很多益处&…...
rk3568点亮E-ink
rk3568 Android11/12 适配 E-ink “EINK”是英语ElectronicInk的缩写。翻译成中文为“电子墨水”。电子墨水由数百万个微胶囊(Microcapsules)所构成,微胶囊的大小约等同于人类头发的直径。每个微胶囊里含有电泳粒子──带负电荷的白色以及带正电荷的黑色粒子&#…...
如何将Springboot项目通过IDEA打包成jar包,并且转换成可执行文件
首先在IDEA打开你的项目,需要确认项目可以正常运行,然后点击页面右侧的Maven,运行Lifecycle下的package, 此时在项目的target目录下就可以看到一个jar包 这个时候你可以在jar包所在目录下执行cmd窗口,运行 java -jar campus-market-0.0.1-S…...

总结:网卡
一、背景 经常听到eth0,bond0这些概念,好奇他们的区别,于是有了此篇文章记录下。 二、介绍 网卡:即网络接口板,又称网络适配器或NIC (网络接口控制器),是一块被设计用来允许计算机在计算机网络上进行通讯…...

Java这么卷,还有前景吗?
“Java很卷”、“大家不要再卷Java了”,经常听到同学这样抱怨。但同时,Java的高薪也在吸引越来越多的同学。不少同学开始疑惑:既然Java这么卷,还值得我入行吗? 首先先给你吃一颗定心丸:现在选择Java依然有…...
--gocron)
后端简易定时任务框架选择(Python/Go)--gocron
文章目录前言实现后语前言 在使用Python的web框架中,包括flask/Django,其中大量用到celery;celery作为异步任务使用的多,同时也会用celery来跑些定时任务,比如每晚定时跑脚本、跑数据统计等闲时任务。但随着任务量的增…...

【GStreamer学习】之GStreamer基础教程
目标 没有什么比在屏幕上打印出“Hello World”更能获得对软件库的第一印象了! 但是由于我们正在学习多媒体框架,所以我们将输出“Hello World!”改为播放视频。 不要被下面的代码量吓到:只有 4 行是真正需要的, 其…...

各类Round-Robin总结,含Verilog实现
1. Fixed Priority Arbitrary 固定优先级就是指每个req的优先级是不变的,即优先级高的先被处理,优先级低的必须是在没有更高优先级的req的时候才会被处理。所以转化为数学模型就是找出req序列中第一个为1的位置,然后将其转换为onehot。 例如: req[3:0] = 4b1100 ==> g…...

《软件设计师-知识点》
1、指令流水线 (一)一条指令的执行过程可分为三个阶段:取指、分析、执行。 取指:根据PC(程序计数器)内容访问主存储器,取出一条指令送到IR(指令寄存器)中。 分析&…...

mysql 同义词_数据库中的同义词synonym
一、Oracle数据只有一个实例(简单理解就是Oracle 只能建立一个数据库,不像MySQL,它下面可以创建N个库),那么Oracle是根据用户灵活去管理的;这点读起来、理解 起来也不那么难,但是除非自己亲自实现一把才理解深入点&…...
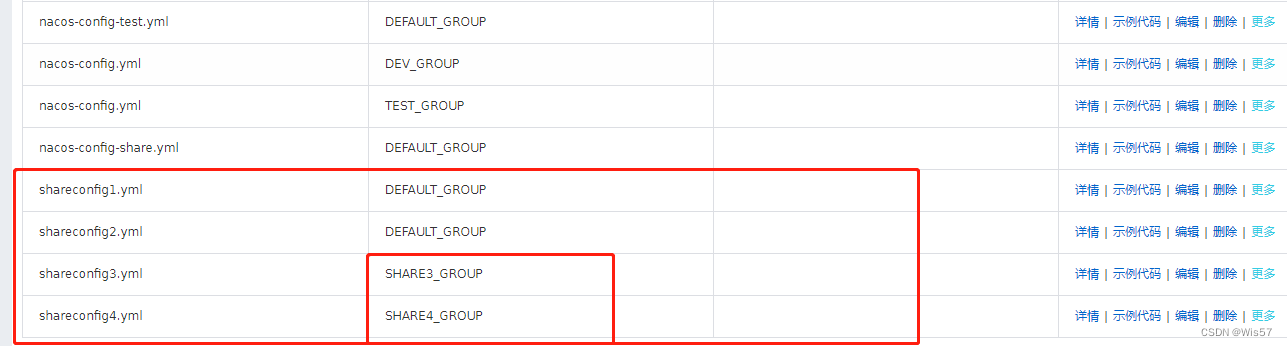
Nacos共享配置
本文介绍一下Nacos作为配置中心时,如何读取共享配置 我的环境 Windows10JDK8SpringCloud:Finchley.RELEASESpringBoot:2.0.4.RELEASEspring-cloud-alibaba-dependencies:0.2.2.RELEASENacos-server:1.0.1 本文的项目…...
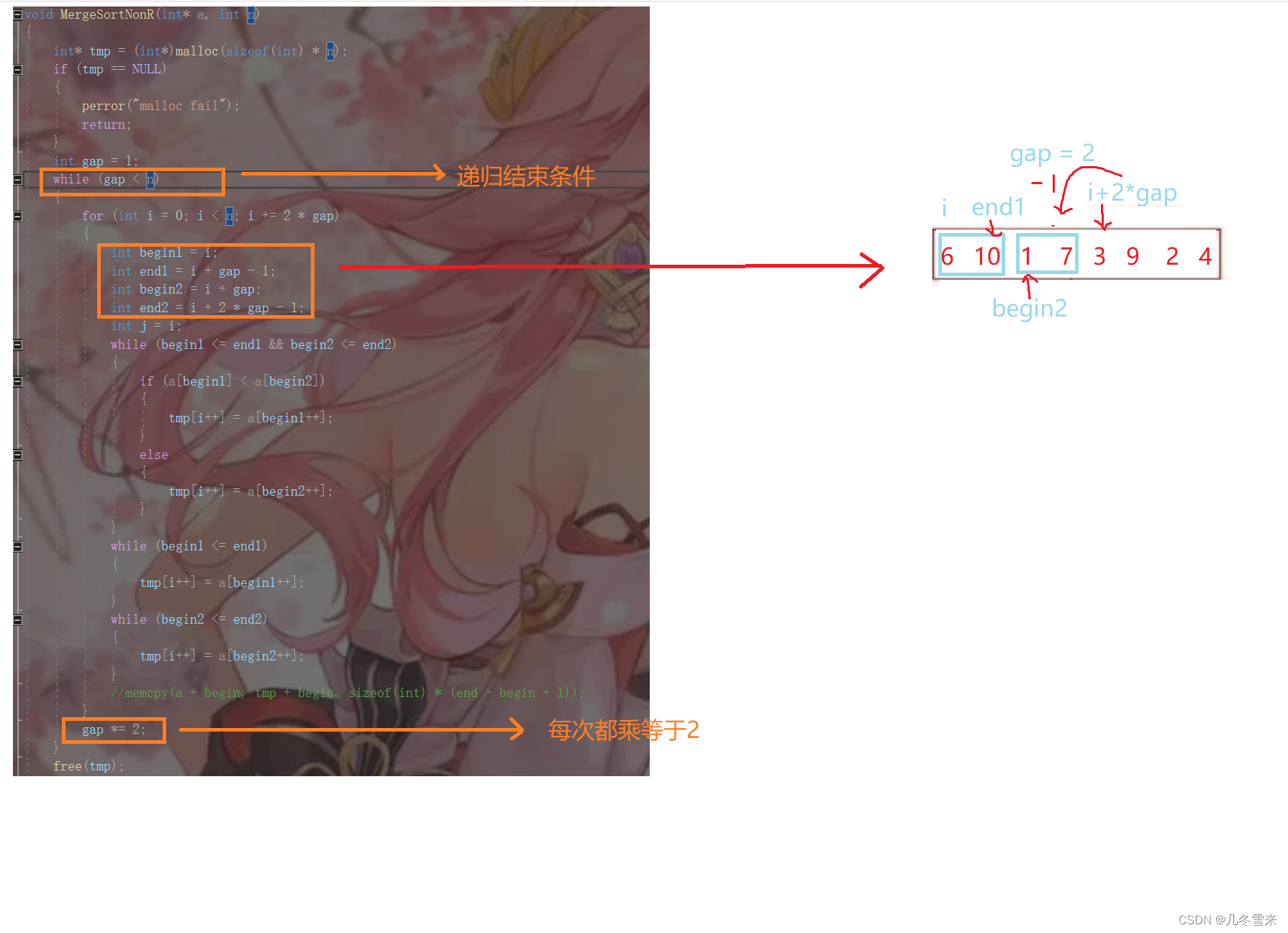
数据结构——排序(4)
作者:几冬雪来 时间:2023年4月12日 内容:数据结构排序内容讲解 目录 前言: 1.快速排序中的递归: 2.小区间优化: 3.递归改非递归: 4.归并排序: 5.归并排序的非递归形式&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
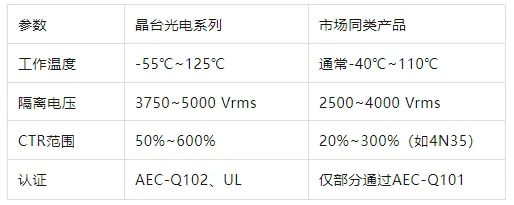
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...
