数据结构 | 排序 - 总结
排序的方式
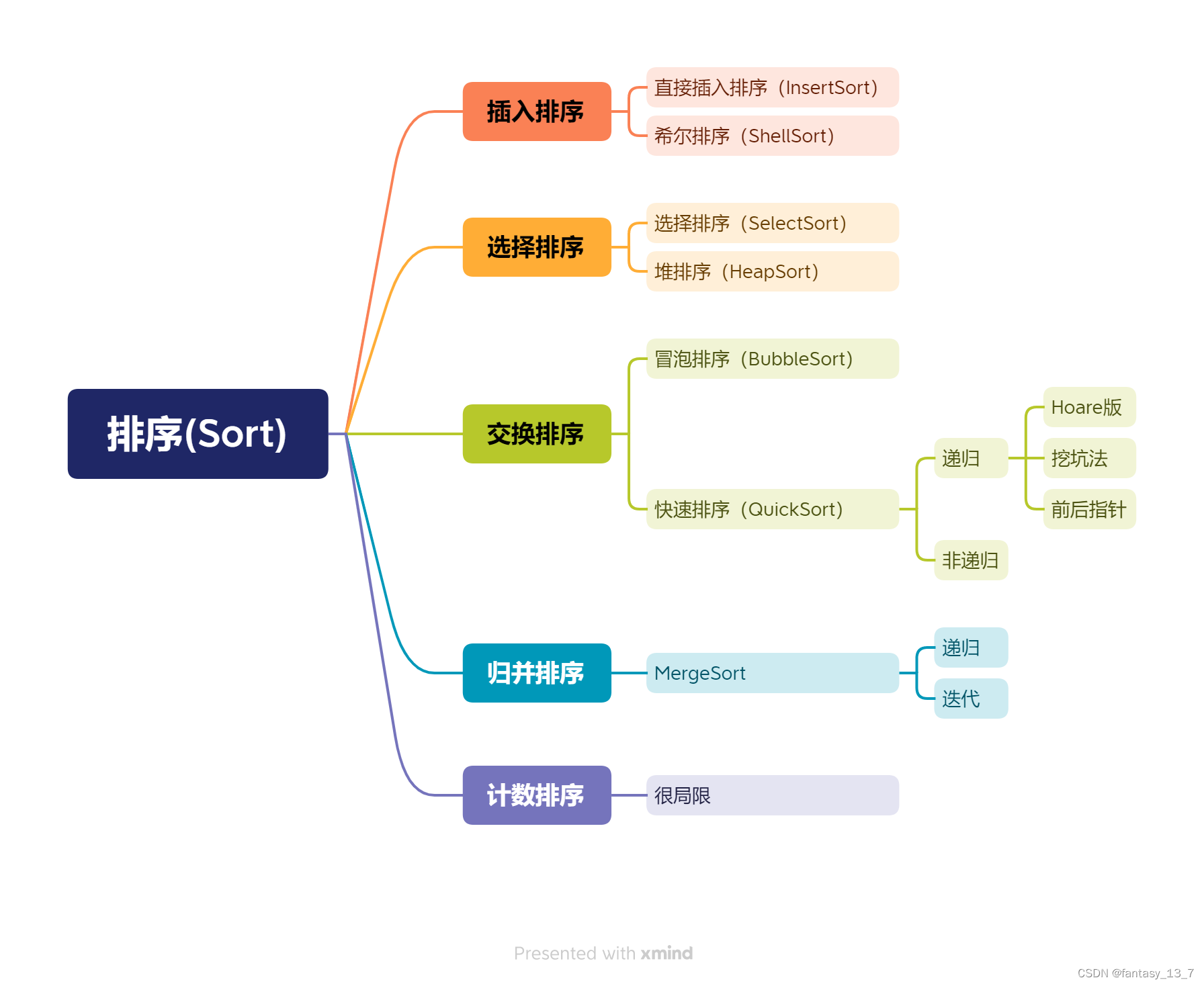
排序的稳定性
-
什么是排序的稳定性?
不改变相同数据的相对顺序 -
排序的稳定性有什么意义?
- 假定一个场景:
一组成绩:100,88,98,98,78,100(按交卷顺序排列,先交在前)
先需要对这组数据按降序排列,如果分数相同,先交卷的排在前面。
- 假定一个场景:
在以上这种场景下,选择具有稳定性的排序方式就很有必要。
排序方式分析比较汇总
| 排序方式 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| Insert | O(N2) | O(1) | √ |
| Shell | O(N1.3) | O(1) | ×(预排序相同数可能分到不同组) |
| Select | O(N2) | O(1) | ×(9,9,4,4)(swap(4,9)后4和4的相对顺序改变) |
| Heap | O(N*logN) | O(1) | × |
| Bubble | O(N2) | O(1) | √ |
| Quick | O(N*logN)(大量重复数据:N2) | O(logN)(递归调用栈帧) | ×(最后相遇那下交换会打乱) |
| Merge | O(N*logN) | O(N+ | √ |
| Count | O(N+range) | O(range) | × |
912.排序数组 - 力扣(LeetCode)
👉题目链接
/*** Note: The returned array must be malloced, assume caller calls free().*///栈
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{STDataType* _a;int _top; // 栈顶int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{STDataType* tmp = (STDataType*)malloc(4 * sizeof(STDataType));if (!tmp){perror("malloc fail");exit(-1);}ps->_a = tmp;ps->_top = 0;ps->_capacity = 4;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{assert(ps);if (ps->_capacity == ps->_top){STDataType* tmp = (STDataType*)realloc(ps->_a, 2 * ps->_capacity * sizeof(STDataType));if (!tmp){perror("realloc fail");exit(-1);}ps->_a = tmp;ps->_capacity *= 2;}ps->_a[ps->_top] = data;ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{assert(ps);assert(!StackEmpty(ps));assert(ps->_top);ps->_top--;}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{assert(ps);assert(ps->_top);return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{assert(ps);return ps->_top;
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{assert(ps);return ps->_top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{assert(ps);free(ps->_a);ps->_capacity = ps->_top = 0;ps->_a = NULL;
}//插入排序
void InsertSort(int* a, int n)
{assert(a);for (int i = 1; i < n; i++){int tmp = a[i];int end = i - 1;while (end >= 0){if (a[end] <= tmp){break;}//a[end + 1] = a[end--];???为什么错误a[end + 1] = a[end];end--;}a[end + 1] = tmp;}}// 希尔排序
void ShellSort(int* a, int n)
{assert(a);int gap = n / 2;while (gap){for (int i = 1; i < n; i++){int tmp = a[i];int end = i - gap;while (end >= 0){if (a[end] <= tmp){break;}a[end + gap] = a[end];end -= gap;}a[end + gap] = tmp;}gap /= 2;}
}void Swap(int* x, int* y)
{assert(x && y);int tmp = *x;*x = *y;*y = tmp;
}// 选择排序
void SelectSort(int* a, int n)
{assert(a);int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = end;//[begin+1,end-1]for (int j = begin; j <= end; j++){if (a[j] < a[mini])mini = j;if (a[j] > a[maxi])maxi = j;}//swap之前 min==a[mini] max==a[maxi]Swap(&a[begin], &a[mini]);//swap之后:begin → min ; mini → original-a[begin]//if(original-a[begin] → max)则会影响 a[maxi] =? maxif (begin == maxi)//如果原本begin指向的数是max,则swap之后这个数已经被交换到了mini所指向的位置maxi = mini;Swap(&a[end], &a[maxi]);++begin;--end;}
}// 堆排序
void AdjustDwon(int* a, int n, int root)
{assert(a);int parent = root;int child = parent * 2 + 1;while (child < n){if ((child + 1) < n && a[child + 1] > a[child])++child;if (a[parent] < a[child])Swap(&a[parent], &a[child]);elsebreak;parent = child;child = parent * 2 + 1;}
}
void HeapSort(int* a, int n)
{assert(a);//建大堆for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--){AdjustDwon(a, n, parent);}int end = n - 1;while (end){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);end--;}
}
// 冒泡排序
void BubbleSort(int* a, int n)
{assert(a);for (int j = 0; j < n; j++){for (int i = 0; i < n - j - 1; i++){if (a[i] > a[i + 1])Swap(&a[i], &a[i + 1]);}}
}// 快速排序递归实现
// 三数取中
int GetMidIndex(int* a, int left, int right)
{int begin = left, end = right;int middle = (left + right) / 2;if (a[begin] < a[end]){if (a[middle] < a[begin])return begin;else if (a[middle] > a[end])return end;elsereturn middle;}else{if (a[middle] < a[end])return end;else if (a[middle] > a[begin])return begin;elsereturn middle;}}
// 快速排序hoare版本
int hoareSort1(int* a, int left, int right)
{assert(a);if (left >= right)return;// if ((right - left + 1) < 5)// {// InsertSort(a + left, right - left + 1);// }else{int key = left, begin = left, end = right;int mid = GetMidIndex(a, left, right);Swap(&a[mid], &a[key]);while (left < right){while (left < right && a[right] >= a[key]){--right;}while (left < right && a[left] <= a[key]){++left;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[right]);//left==right//[begin,left-1] [right+1,end]hoareSort1(a, begin, left - 1);hoareSort1(a, right + 1, end);}return right;
}// 快速排序挖坑法
int HoleSort2(int* a, int left, int right)
{if (left >= right)return;int key = a[left];int hole = left, begin = left, end = right;while (left < right){while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[right] = key;//[begin,left-1] [right+1,end]HoleSort2(a, begin, left - 1);HoleSort2(a, right + 1, end);return right;
}// 快速排序前后指针法
int PointSort3(int* a, int left, int right)
{assert(a);if (left >= right)return;int keyi = left;int prev = left, cur = left;while (cur <= right){if (a[cur] < a[keyi] && cur != prev)Swap(&a[++prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);//[left,prev-1][prev+1,right]PointSort3(a, left, prev - 1);PointSort3(a, prev + 1, right);return prev;
}// 快速排序 非递归实现
void QuickSort(int* a, int left, int right)
{assert(a);Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (!StackEmpty(&st)){int end = StackTop(&st);StackPop(&st);int begin = StackTop(&st);StackPop(&st);int keyi = hoareSort1(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]if (keyi + 1 < end){StackPush(&st, keyi + 1);StackPush(&st, end);}if (begin < keyi - 1){StackPush(&st, begin);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}
// 归并排序递归实现
void _MergeSort(int* a, int left, int right, int* tmp)
{assert(a && tmp);if (left == right)return;int middle = (left + right) / 2;//[left, middle] [middle+1,right]//[begin1,end1] [begin2,end2]int begin1 = left, end1 = middle, begin2 = middle + 1, end2 = right;//递归分解_MergeSort(a, begin1, end1, tmp);_MergeSort(a, begin2, end2, tmp);//mergeint i = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");exit(-1);}_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int) * n);if (!tmp){perror("malloc fail");exit(-1);}int range = 1;while (range < n){for (int i = 0; i < n; i += 2 * range){int begin1 = i, end1 = i + range - 1;int begin2 = i + range, end2 = i + 2 * range - 1;int j = begin1;//越界//end1越界if (end1 >= n){end1 = n - 1;begin2 = end2 + 1;//begin2 > end2;}else if (begin2 == n){begin2 = end2 + 1;//begin2 > end2;}else if (end2 >= n){end2 = n - 1;}//mergewhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}memcpy(a, tmp, sizeof(int)*n);range *= 2;}free(tmp);tmp = NULL;
}// 计数排序
void CountSort(int* a, int n)
{assert(a);int min = a[0], max = a[0];for (size_t i = 0; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int size = max - min + 1;int* tmp = (int*)calloc(size, sizeof(int));if (!tmp){perror("calloc fail");exit(-1);}//计数for (size_t i = 0; i < n; i++){++tmp[*(a + i) - min];}int j = 0;for (size_t i = 0; i < size; i++){while (tmp[i]--){a[j++] = i + min;}}free(tmp);tmp = NULL;
}int* sortArray(int* nums, int numsSize, int* returnSize){*returnSize=numsSize;//InsertSort(nums,numsSize);//超出时间限制//ShellSort(nums,numsSize);//SelectSort(nums,numsSize);//超出时间限制//HeapSort(nums,numsSize);//BubbleSort(nums,numsSize);//超出时间限制//hoareSort1(nums,0,numsSize-1);//对于大量重复数据,超出时间限制//HoleSort2(nums,0,numsSize-1);//超出时间限制//PointSort3(nums,0,numsSize-1);//对于大量有序数据,超出时间限制//QuickSort(nums,0,numsSize-1);//对于大量重复数据,超出时间限制//MergeSort(nums,numsSize);//MergeSortNonR(nums,numsSize);//CountSort(nums,numsSize);return nums;
}
相关文章:

数据结构 | 排序 - 总结
排序的方式 排序的稳定性 什么是排序的稳定性? 不改变相同数据的相对顺序 排序的稳定性有什么意义? 假定一个场景: 一组成绩:100,88,98,98,78,100(按交卷顺序…...
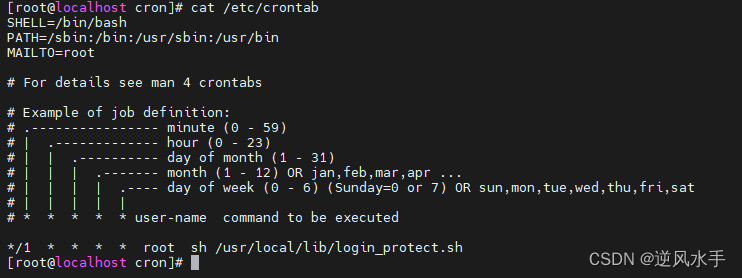
crontab -e 系统定时任务
crontab -e解释 crontab 是由 “cron” 和 “table” 两个单词组成的缩写。其中,“cron” 是一个在 Linux 和类 Unix 操作系统中用于定时执行任务的守护进程,而 “table” 则是指一个表格或者列表,因此 crontab 就是一个用于配置和管理定时任…...
前后端交互系列之Axios详解(包括拦截器)
目录 前言一,服务器的搭建二,Axios的基本使用2.1 Axios的介绍及页面配置2.2 如何安装2.3 Axios的前台代码2.4 Axios的基本使用2.5 axios请求响应结果的结构2.6 带参数的axios请求2.7 axios修改默认配置 三,axios拦截器3.1 什么是拦截器3.2 拦…...
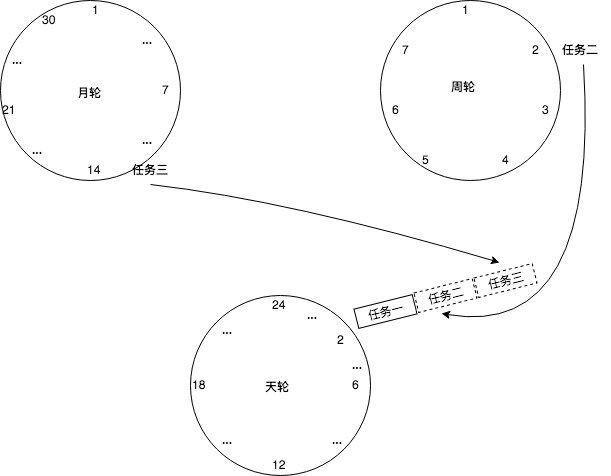
定时任务之时间轮算法
初识时间轮 我们先来考虑一个简单的情况,目前有三个任务A、B、C,分别需要在3点钟,4点钟和9点钟执行,可以把时间想象成一个钟表。 如上图中所示,我只需要把任务放到它需要被执行的时刻,然后等着时针转到这个…...
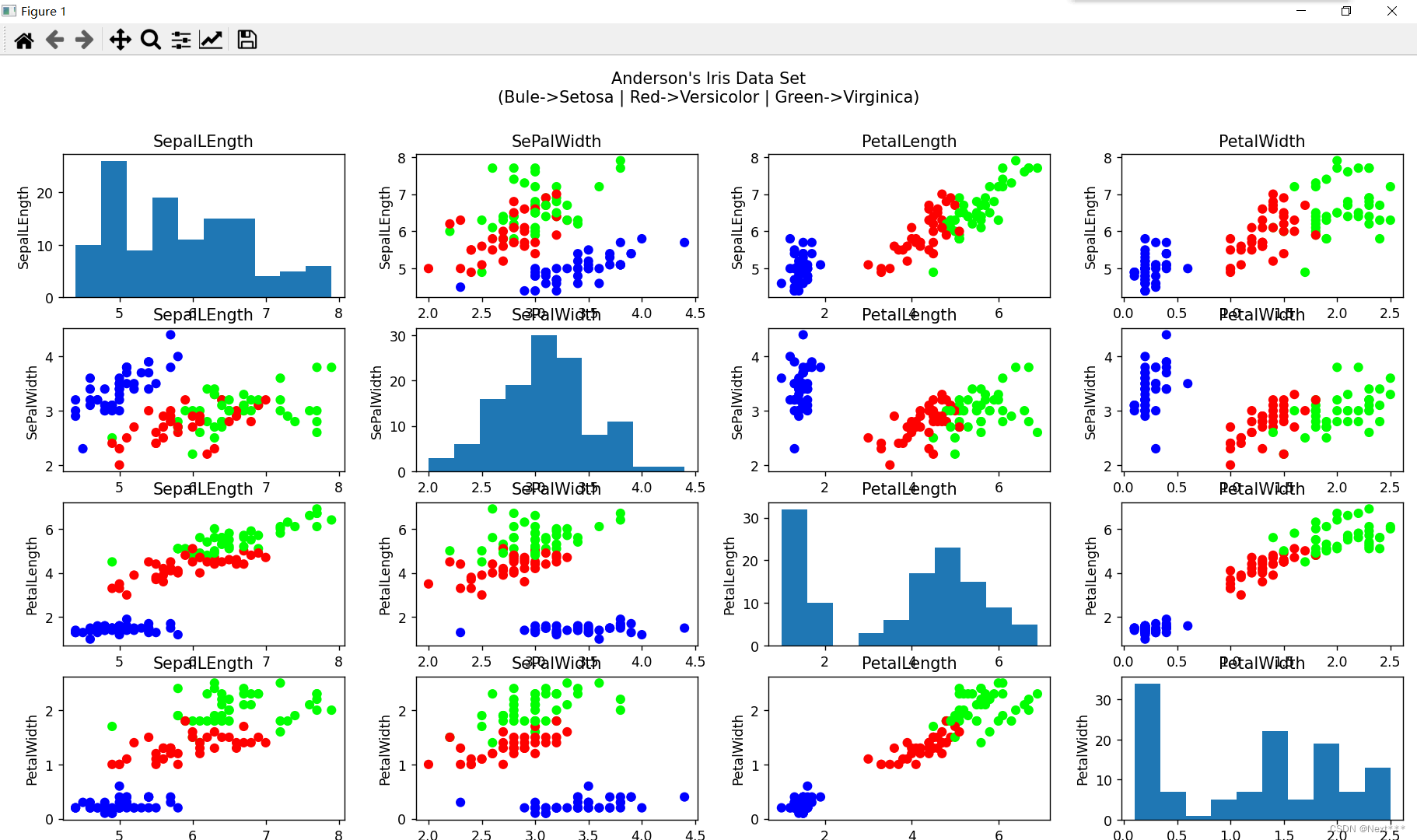
实验4 Matplotlib数据可视化
1. 实验目的 ①掌握Matplotlib绘图基础; ②运用Matplotlib,实现数据集的可视化; ③运用Pandas访问csv数据集。 2. 实验内容 ①绘制散点图、直方图和折线图,对数据进行可视化; ②下载波士顿数房价据集,并…...

【软件工程】为什么要选择软件工程专业?
个人主页:【😊个人主页】 文章目录 前言软件工程💻💻💻就业岗位👨💻👨💻👨💻就业前景🛩️🛩️🛩️工作环…...

5类“计算机”专业很吃香,人才缺口巨大,就业前景良好
说到目前最热门的专业,计算机绝对占有一席之地,是公认的发展前景好、人才缺口大的专业。有人称该专业人数如此众多,势必会导致人才饱和,但是从当前社会互联网发展的趋势来看,计算机专业在很长一段时间都是发展很好的专…...

数仓选型对比
1、数仓选型对比如下(先列举表格,后续逐个介绍) 数仓应用目标产品特点适用于 适用数据类型数据处理速度性能拓展 实施难度运维难度性能优化成本传统数仓(SQLServer、Oracle等关系型数据库)面向主题设计的,为 分析数据而设计基于Oracle、 SQLServer、MyS…...
Java详解与代码实现)
二叉树的遍历(前序、中序、后序)Java详解与代码实现
递归遍历 前序,中序,后序 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, Tree…...

如何找出消耗CPU最多的线程?
如何找出消耗CPU最多的线程? 1.使用 top -c 找出所有当前进程的运行列表 top -c 2.按P(Shiftp)对所有进程按CPU使用率进行排序,找出消耗最高的线程PID 显示Java进程 PID 为 136 的java进程消耗最 3.使用 top -Hp PID,查出里面消…...

【论文笔记】Attention Augmented Convolutional Networks(ICCV 2019 入选文章)
目录 一、摘要 二、介绍 三、相关工作 卷积网络Convolutional networks: 网络中注意力机制Attention mechanisms in networks: 四、方法 1. 图像的自注意力Self-attention over images: 二维位置嵌入Two-dimensional Positional Enco…...

虚幻图文笔记:Character Creator 4角色通过AutoSetup For Unreal Engine插件导入UE5.1的过程笔记
在UE5端安装AutoSetup For Unreal Engine插件 AutoSetup For Unreal Engine是Reallusion官方提供的免费插件,官方下载地址,下载到的是一个可执行文件,点击安装,记住安装的位置⬇ 看装完毕后会打开一个文件夹,这里就是对…...
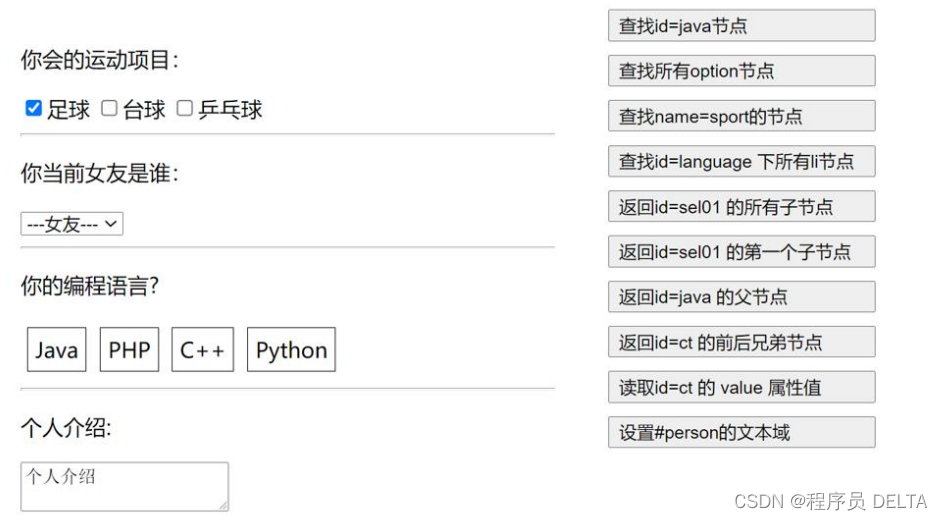
JAVAWeb04-DOM
1. DOM 1.1 概述 1.1.1 官方文档 地址: https://www.w3school.com.cn/js/js_htmldom.asp 1.1.2 DOM 介绍 DOM 全称是 Document Object Model 文档对象模型就是把文档中的标签,属性,文本,转换成为对象来管理 1.2 HTML DOM(文档…...

C++内存管理基础知识
C 内存管理 C内存管理是一个重要的主题,因为它涉及到程序运行时资源的分配和释放。它可以分为三种类型:静态内存、栈内存和堆内存。 静态内存 静态内存(Static Memory):静态内存用于存储全局变量、静态变量和常量。这…...
命令执行漏洞概述
命令执行漏洞概述 命令执行定义命令执行条件命令执行成因命令执行漏洞带来的危害远程命令执行漏洞相关函数assert()preg_replace()call_user_func() a ( a( a(b)可变函数远程命令执行漏洞的利用系统命令执行漏洞相关函数system()exec()shell_exec()passthru(&#x…...

【初试复试第一】脱产在家二战上岸——上交819考研经验
笔者来自通信考研小马哥23上交819全程班学员 先介绍一下自己,我今年初试426并列第一,加上复试之后总分600,电子系第一。 我本科上交,本科期间虽然没有挂科但是成绩排名处于中下游水平。参加过全国电子设计大赛,虽然拿…...
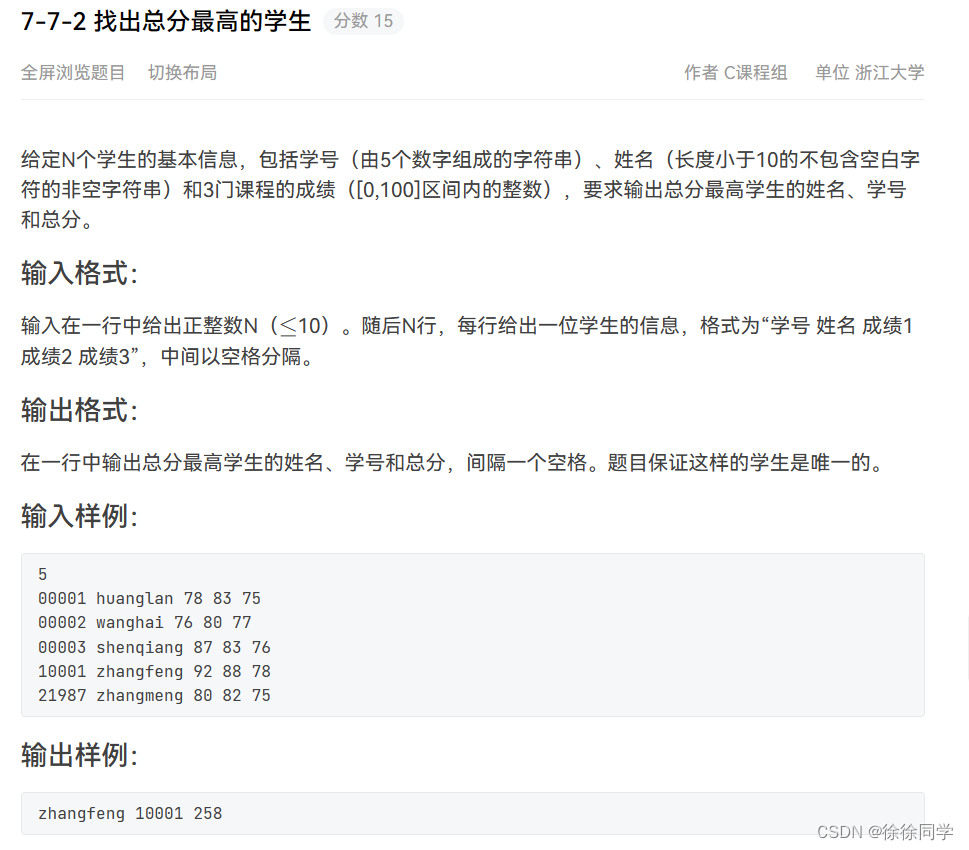
PTA:C课程设计(7)
山东大学(威海)2022级大一下C习题集(7) 函数题7-6-1 递增的整数序列链表的插入7-6-2 查找学生链表7-6-3 统计专业人数7-6-4 建立学生信息链表 编程题7-7-1 查找书籍7-7-2 找出总分最高的学生 函数题 7-6-1 递增的整数序列链表的插…...

POSTGRESQL LINUX 与 PG有关的内存参释义
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

Docker的常见命令
前言:使用Docker得学会的几个常见命令 常见命令前置学习: docker --help这个命令必须得会因为,很多命令是记不住的,得使用他们的官方help下面是一些实例 docker load --help常见命令集合: 一: docker images #查看全部镜像 docker rmi #删除某个镜像(例如:docker rmi redis…...
详细介绍性能测试的方法(含文档)
性能测试是软件测试中的一个重要环节,其目的是评估系统在不同负荷下的性能表现,包括响应时间、吞吐量、并发数等指标。通常可以通过以下几种方法进行性能测试: 1、负载测试 负载测试是模拟多用户同时访问系统,测试系统在高并发、…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
