二叉树的遍历(前序、中序、后序)Java详解与代码实现
递归遍历
前序,中序,后序
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*///前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();preorder(root,res);return res;}void preorder(TreeNode root, List<Integer> res){if(root==null){return;}res.add(root.val);preorder(root.left,res);preorder(root.right,res);}
}
//中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();inorder(root,res);return res;}void inorder(TreeNode root,List<Integer> res){if(root==null){return;}inorder(root.left,res);res.add(root.val);inorder(root.right,res);}
}
//后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();postOrder(root,res);return res;}void postOrder(TreeNode root,List<Integer> res){if(root==null){return;}postOrder(root.left,res);postOrder(root.right,res);res.add(root.val);}
}
这三个遍历,理解起来都是差不多的
以前序遍历为例
以每一个树或子树的根节点和List集合作为函数的参数返回值类型是void.
如果碰到每一个树或子树的根节点是空,就结束递归,结束函数
否则,先把根节点的值收入集合,再把左右结点(子树)的值收入集合
最后调用函数之后,返回这个集合
迭代法(非递归)
前序,后序
前序
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<>();if (root==null){return result;}Stack<TreeNode> stack=new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node=stack.pop();result.add(node.val);if (node.right!=null){stack.push(node.right);}if (node.left!=null){stack.push(node.left);}}return result;}
}
用栈模拟(实现)递归
先把树或某一子树的根节点入栈,然后,进入数组
再分别把右左子树的根节点入栈,然后分别将二者进入数组(右先入栈左后入栈,才能保证左先入数组,右后入数组)
这样左中右结点进入数组的顺序为:中左右
后序
以此类推,入栈的顺序为中左右,这样入数组的顺序为中右左,然后再将数组逆序对调
这样,数组输出的顺序就是左右中
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<>();if (root==null){return result;}Stack<TreeNode> stack=new Stack<>();stack.push(root);while(!stack.isEmpty()){TreeNode node=stack.pop();result.add(node.val);if (node.left!=null){stack.push(node.left);}if (node.right!=null){stack.push(node.right);}}Collections.reverse(result);return result;}
}
要注意的是,Java中,List没有将集合元素逆序对调的方法,所以,要使用Collections的reverse方法
中序
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();if (root==null){return res;}Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null||!stack.isEmpty()){if (cur!=null){stack.push(cur);cur=cur.left;}else{//就是,cur为空的时候cur=stack.pop();//出栈,并让cur指向他res.add(cur.val);//这里是处理中间结点cur=cur.right;//既然没有左子节点,那就看看有没有右子节点}}return res;}
}
这里的遍历方式和前序后序不一样了
前序后序差不多算是遍历到哪个结点就处理哪个节点。这里不一样,这里是先处理左节点,左子树的左子树的左子树的左……左节点……所以,要先遍历到最左的左节点,然后再看最左节点的根节点然后他的根结点的右子节点。
这里还用到了一个指针来指向要处理的树的结点
二叉树迭代遍历法的统一写法风格
我们以中序遍历为例,在二叉树:听说递归能做的,栈也能做! (opens new window)中提到说使用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。
那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法
Java: 迭代法前序遍历代码如下:
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)st.push(node); // 添加中节点st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。} else { // 只有遇到空节点的时候,才将下一个节点放进结果集st.pop(); // 将空节点弹出node = st.peek(); // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;}
}
迭代法中序遍历代码如下:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)st.push(node); // 添加中节点st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)} else { // 只有遇到空节点的时候,才将下一个节点放进结果集st.pop(); // 将空节点弹出node = st.peek(); // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;
}
}
迭代法后序遍历代码如下:
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中st.push(node); // 添加中节点st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈) } else { // 只有遇到空节点的时候,才将下一个节点放进结果集st.pop(); // 将空节点弹出node = st.peek(); // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;}
}
相关文章:
Java详解与代码实现)
二叉树的遍历(前序、中序、后序)Java详解与代码实现
递归遍历 前序,中序,后序 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, Tree…...

如何找出消耗CPU最多的线程?
如何找出消耗CPU最多的线程? 1.使用 top -c 找出所有当前进程的运行列表 top -c 2.按P(Shiftp)对所有进程按CPU使用率进行排序,找出消耗最高的线程PID 显示Java进程 PID 为 136 的java进程消耗最 3.使用 top -Hp PID,查出里面消…...

【论文笔记】Attention Augmented Convolutional Networks(ICCV 2019 入选文章)
目录 一、摘要 二、介绍 三、相关工作 卷积网络Convolutional networks: 网络中注意力机制Attention mechanisms in networks: 四、方法 1. 图像的自注意力Self-attention over images: 二维位置嵌入Two-dimensional Positional Enco…...

虚幻图文笔记:Character Creator 4角色通过AutoSetup For Unreal Engine插件导入UE5.1的过程笔记
在UE5端安装AutoSetup For Unreal Engine插件 AutoSetup For Unreal Engine是Reallusion官方提供的免费插件,官方下载地址,下载到的是一个可执行文件,点击安装,记住安装的位置⬇ 看装完毕后会打开一个文件夹,这里就是对…...
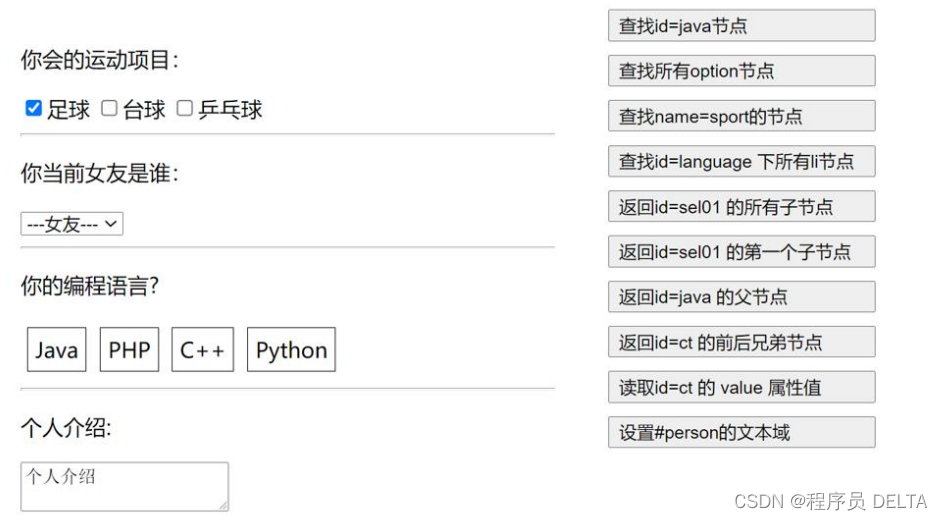
JAVAWeb04-DOM
1. DOM 1.1 概述 1.1.1 官方文档 地址: https://www.w3school.com.cn/js/js_htmldom.asp 1.1.2 DOM 介绍 DOM 全称是 Document Object Model 文档对象模型就是把文档中的标签,属性,文本,转换成为对象来管理 1.2 HTML DOM(文档…...

C++内存管理基础知识
C 内存管理 C内存管理是一个重要的主题,因为它涉及到程序运行时资源的分配和释放。它可以分为三种类型:静态内存、栈内存和堆内存。 静态内存 静态内存(Static Memory):静态内存用于存储全局变量、静态变量和常量。这…...
命令执行漏洞概述
命令执行漏洞概述 命令执行定义命令执行条件命令执行成因命令执行漏洞带来的危害远程命令执行漏洞相关函数assert()preg_replace()call_user_func() a ( a( a(b)可变函数远程命令执行漏洞的利用系统命令执行漏洞相关函数system()exec()shell_exec()passthru(&#x…...

【初试复试第一】脱产在家二战上岸——上交819考研经验
笔者来自通信考研小马哥23上交819全程班学员 先介绍一下自己,我今年初试426并列第一,加上复试之后总分600,电子系第一。 我本科上交,本科期间虽然没有挂科但是成绩排名处于中下游水平。参加过全国电子设计大赛,虽然拿…...
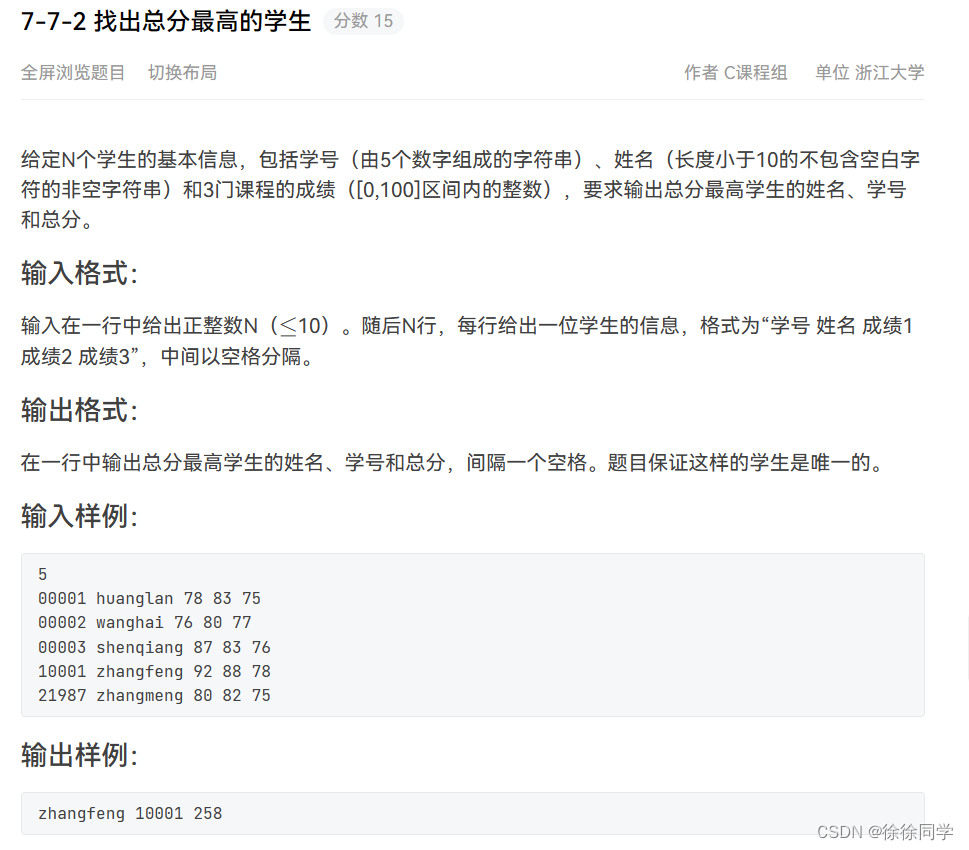
PTA:C课程设计(7)
山东大学(威海)2022级大一下C习题集(7) 函数题7-6-1 递增的整数序列链表的插入7-6-2 查找学生链表7-6-3 统计专业人数7-6-4 建立学生信息链表 编程题7-7-1 查找书籍7-7-2 找出总分最高的学生 函数题 7-6-1 递增的整数序列链表的插…...

POSTGRESQL LINUX 与 PG有关的内存参释义
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

Docker的常见命令
前言:使用Docker得学会的几个常见命令 常见命令前置学习: docker --help这个命令必须得会因为,很多命令是记不住的,得使用他们的官方help下面是一些实例 docker load --help常见命令集合: 一: docker images #查看全部镜像 docker rmi #删除某个镜像(例如:docker rmi redis…...
详细介绍性能测试的方法(含文档)
性能测试是软件测试中的一个重要环节,其目的是评估系统在不同负荷下的性能表现,包括响应时间、吞吐量、并发数等指标。通常可以通过以下几种方法进行性能测试: 1、负载测试 负载测试是模拟多用户同时访问系统,测试系统在高并发、…...

深入剖析 Qt QHash :原理、应用与技巧
目录标题 引言QHash 基础用法基础用法示例基础用法综合示例 QHash 的高级用法迭代器:遍历 QHash 中的元素(Iterators: Traversing Elements in QHash )QHash和其他容器的对比QHash 和 std::unordered\_map QHash的底层原理和内存管理QHash 的…...
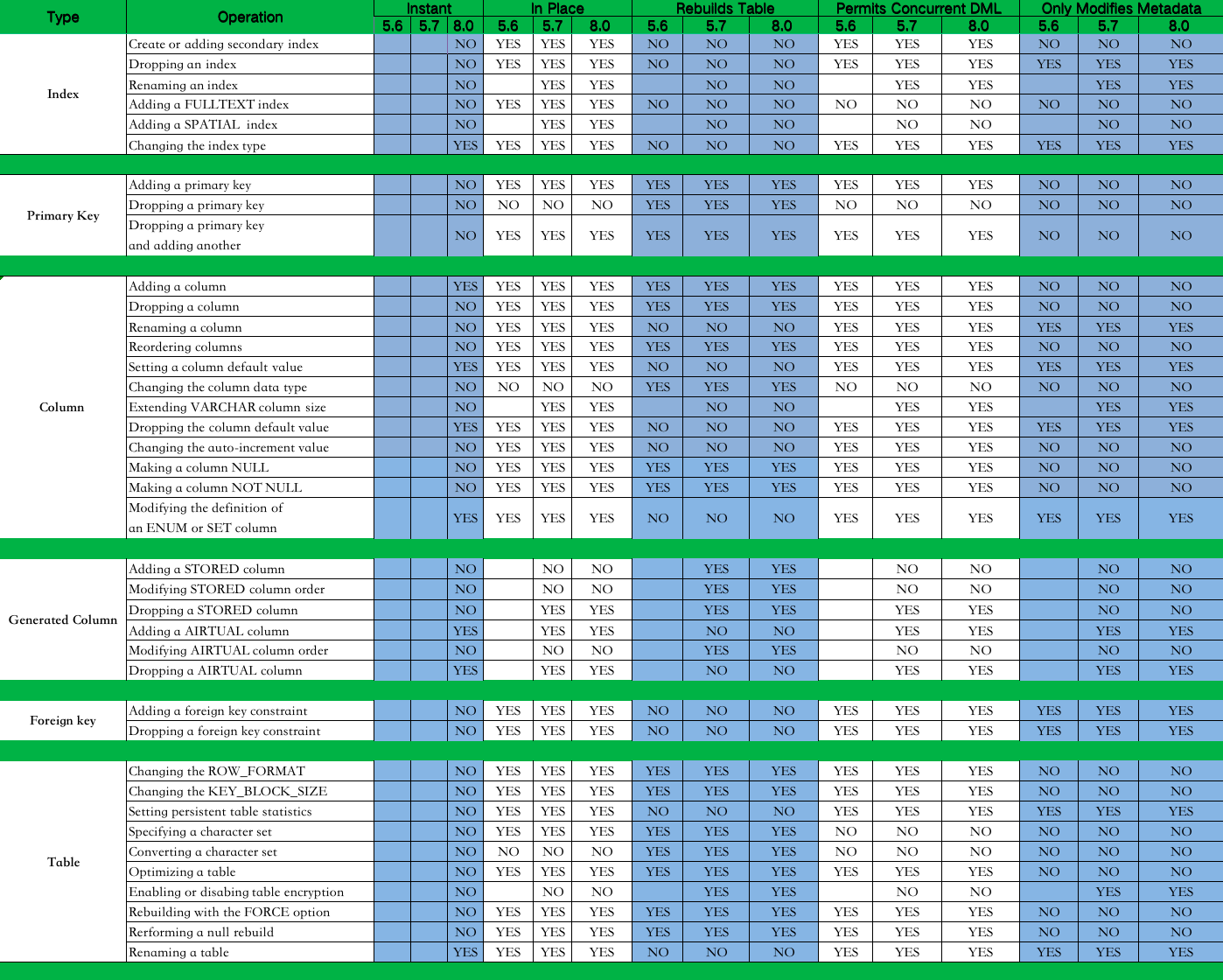
技术分享 | MySQL级联复制下进行大表的字段扩容
作者:雷文霆 爱可生华东交付服务部 DBA 成员,主要负责Mysql故障处理及相关技术支持。爱好看书,电影。座右铭,每一个不曾起舞的日子,都是对生命的辜负。 本文来源:原创投稿 *爱可生开源社区出品,…...
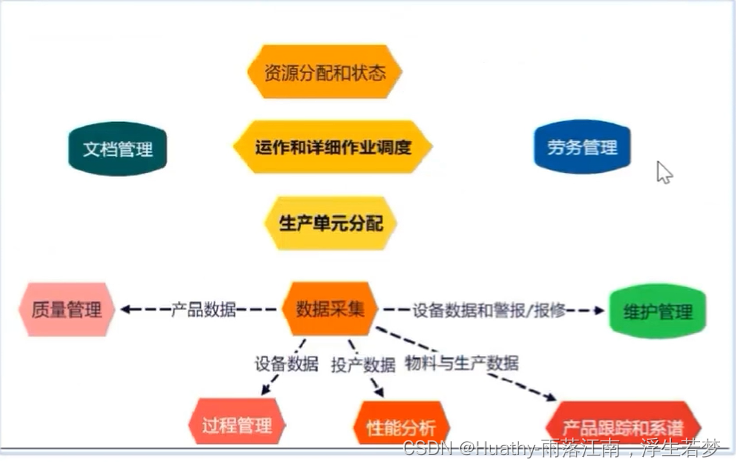
工业互联网业务知识
文章目录 背景第四次工业革命带动制造业产业升级主要工业大国不同路径 架构ISA95体系架构变革趋势基础通用架构数据采集平台 工业互联网应用软件工业互联网全要素连接产品视角:产销服务企业的业务流程企业数字化改造:车间级全要素连接 工业互联网的产品体…...
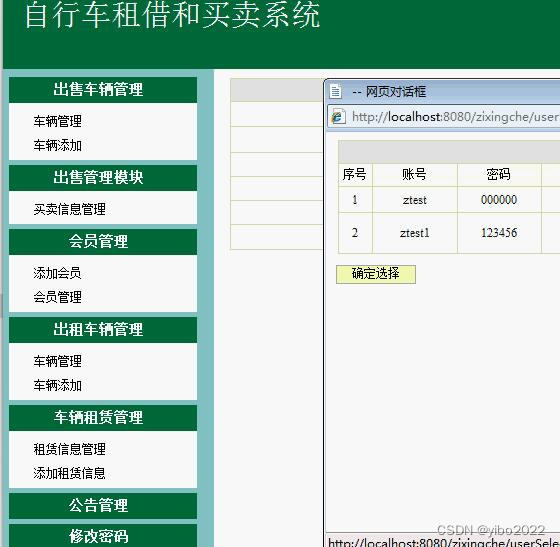
jsp+java自行车租赁租借和买卖系统
自行车租借和买卖系统 系统包括四个模块。1,系统模块,2,车辆管理模块,3.租借车管理模块,4,买卖车管理模块。 1,系统模块包括: 连接数据库,工作人员登录,退出。 2&#…...
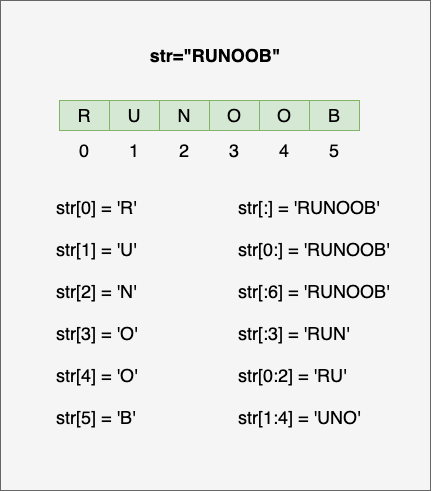
Python3 字符串
Python3 字符串 字符串是 Python 中最常用的数据类型。我们可以使用引号( 或 " )来创建字符串。 创建字符串很简单,只要为变量分配一个值即可。例如: var1 Hello World! var2 "Runoob" Python 访问字符串中的值 Python 不支持单字符…...

Day943.持续集成流水线 -系统重构实战
持续集成流水线 Hi,我是阿昌,今天学习记录的是关于持续集成流水线的内容。 从团队协作的角度上来看,在版本发布过程中,经常出现测试依赖开发手工生成制品、版本发布也从开发本地出版本的问题。而且项目架构如果从单体演进至组件…...

How to use CCS to debug a running M4F core that was started by Linux?
参考FAQ:AM62x & AM64x: How to use CCS to debug a running M4F core that was started by Linux? 问题记录: 1.使用SD卡启动模式,板上运行Linux。 当Linux系统启动后,9表示M4F core: am64xx-evm login: root rootam64xx…...

216、组合总数III
难度:中等 找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9 每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
