已知原根多项式和寄存器初始值时求LFSR的简单例子
线性反馈移位寄存器(LFSR)是一种用于生成伪随机数序列的简单结构。在这里,我们有一个四项原根多项式 p ( x ) = 1 + x + 0 x 2 = 11 0 2 p(x) = 1 + x + 0x^2 = 110_2 p(x)=1+x+0x2=1102 和初始值 S 0 = 100 S_0 = 100 S0=100。我们将使用 LFSR 动作过程来生成一个伪随机序列。
LFSR 的动作过程如下:
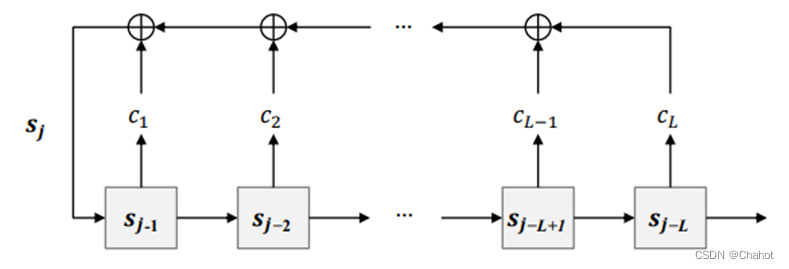
将初始值加载到寄存器中。
对于每次时钟周期:
a. 将寄存器中的当前值与原根多项式的非零项进行异或(XOR)操作。
b. 将结果右移一位,然后将异或(XOR)操作的结果放入最高位。
现在,我们将详细描述 LFSR 的动作过程:
加载初始值: S 0 = 100 S_0 = 100 S0=100。
时钟周期 1:
a. 异或操作: 1 ⊕ 0 = 1 1 \oplus 0 = 1 1⊕0=1, 作用目标是寄存器从左到右的第一第二位
b. 右移并更新最高位: S 1 = 110 S_1 = 110 S1=110。
时钟周期 2:
a. 异或操作: 1 ⊕ 1 = 0 1 \oplus 1 = 0 1⊕1=0。
b. 右移并更新最高位: S 2 = 011 S_2 = 011 S2=011。
时钟周期 3:
a. 异或操作: 0 ⊕ 1 = 1 0 \oplus 1 = 1 0⊕1=1。
b. 右移并更新最高位: S 3 = 101 S_3 = 101 S3=101。
时钟周期 4:
a. 异或操作: 1 ⊕ 0 = 1 1 \oplus 0 = 1 1⊕0=1。
b. 右移并更新最高位: S 4 = 110 S_4 = 110 S4=110。从这一位开始进入循环
在时钟周期 4 后,寄存器的值回到了初始值运算后的第一个计算值 S 1 = 110 S_1 = 110 S1=110,因此序列将开始重复。所以,LFSR 生成的伪随机序列为:
100,110,011,101,110,…
4bit的例子
线性反馈移位寄存器(LFSR)是一种用于生成伪随机数序列的简单结构。在这里,我们有一个四项原根多项式 p ( x ) = 1 + x + 0 x 2 + x 3 = 110 1 2 p(x) = 1 + x + 0x^2 + x^3 = 1101_2 p(x)=1+x+0x2+x3=11012 和初始值 S 0 = 0100 S_0 = 0100 S0=0100。我们将使用 LFSR 动作过程来生成一个伪随机序列。
LFSR 的动作过程如下:
将初始值加载到寄存器中。
对于每次时钟周期:
a. 将寄存器中的当前值与原根多项式的非零项进行异或(XOR)操作。
b. 将结果右移一位,然后将异或(XOR)操作的结果放入最高位。
现在,我们将详细描述 LFSR 的动作过程:
加载初始值: S 0 = 0100 S_0 = 0100 S0=0100。
时钟周期 1:
a. 异或操作: 0 ⊕ 1 ⊕ 0 = 1 0 \oplus 1 \oplus 0 = 1 0⊕1⊕0=1。
b. 右移并更新最高位: S 1 = 1010 S_1 = 1010 S1=1010。
时钟周期 2:
a. 异或操作: 1 ⊕ 0 ⊕ 0 = 1 1 \oplus 0 \oplus 0 = 1 1⊕0⊕0=1。
b. 右移并更新最高位: S 2 = 1110 S_2 = 1110 S2=1110。
时钟周期 3:
a. 异或操作: 1 ⊕ 1 ⊕ 1 = 0 1 \oplus 1 \oplus 1 = 0 1⊕1⊕1=0。
b. 右移并更新最高位: S 3 = 0111 S_3 = 0111 S3=0111。
时钟周期 4:
a. 异或操作: 0 ⊕ 1 ⊕ 1 = 0 0 \oplus 1 \oplus 1 = 0 0⊕1⊕1=0。
b. 右移并更新最高位: S 4 = 0011 S_4 = 0011 S4=0011。
时钟周期 5:
a. 异或操作: 0 ⊕ 0 ⊕ 1 = 1 0 \oplus 0 \oplus 1 = 1 0⊕0⊕1=1。
b. 右移并更新最高位: S 5 = 1001 S_5 = 1001 S5=1001。
时钟周期 6:
a. 异或操作: 1 ⊕ 0 ⊕ 1 = 0 1 \oplus 0 \oplus 1 = 0 1⊕0⊕1=0。
b. 右移并更新最高位: S 6 = 0100 S_6 = 0100 S6=0100。
在时钟周期 ,6后,寄存器的值回到了初始值 S 0 = 0100 S_0 = 0100 S0=0100,因此序列将开始重复。所以,LFSR 生成的伪随机序列为:
0100, 1010, 1110, 0111, 0011, 1001。周期为6,小于最大周期15。
相关文章:

已知原根多项式和寄存器初始值时求LFSR的简单例子
线性反馈移位寄存器(LFSR)是一种用于生成伪随机数序列的简单结构。在这里,我们有一个四项原根多项式 p ( x ) 1 x 0 x 2 11 0 2 p(x) 1 x 0x^2 110_2 p(x)1x0x21102 和初始值 S 0 100 S_0 100 S0100。我们将使用 LFSR 动作过…...
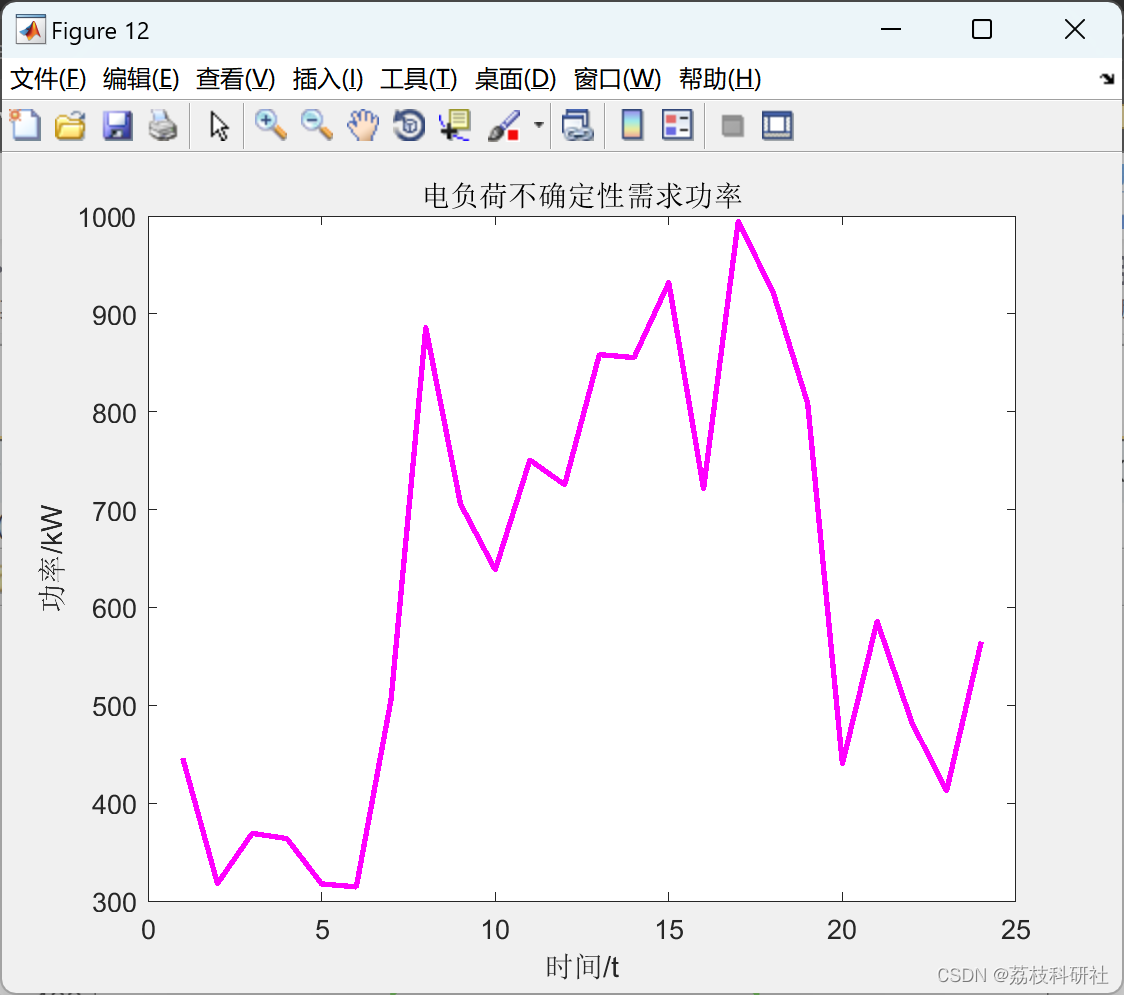
【场景生成与削减】基于蒙特卡洛法场景生成及启发式同步回带削减风电、光伏、负荷研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

探索C/C++ main函数:成为编程高手的关键步骤
探索C/C main函数:成为编程高手的关键步骤(Exploring the C/C Main Function: A Key Step to Becoming a Programming Master) 引言(Introduction)main函数的基本概念(Basic Concepts of the main function…...
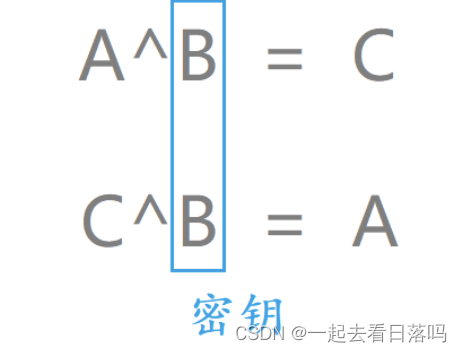
【Linux】应用层协议—http
🎇Linux: 博客主页:一起去看日落吗分享博主的在Linux中学习到的知识和遇到的问题博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 看似不起波澜的日复一日,一定会在某一天让你看见坚持…...

七、Django进阶:第三方库Django-extensions的开发使用技巧详解(附源码)
Django-extensions是 Django 的扩展应用,给django开发者提供了许多便捷的扩展工具(extensions),它提供了许多有用的工具和命令行工具,帮助 Django 开发者更高效地进行开发和调试。它的作用包括: - 提供了更多的Django命令&#x…...

浏览器特色状态
强缓存:不会向服务器发送请求,直接从缓存中读取资源,在chrome控制台的Network选项中可以看到该请求返回200的状态码,并且Size显示from disk cache或from memory cache。 强缓存可以通过设置两种HTTP Header实现:Expir…...

context 浅析
在缺少直接调用关系的两个函数之间传递数据,一般都会考虑使用 context,而 context 也被用来存储整个请求链路的公参信息,用户 uid、链路 traceID、特定的业务参数等。函数第一个参数类型设置为 context.Context 也是 Go 的默认写法࿰…...
Bandizip已管理员身份运行
系列文章目录 文章目录 系列文章目录前言一、Bandzib是什么?二、使用步骤1.引入库 前言 在解压krita源码包时Bandizip报错 一、Bandzib是什么? bandzip官网 Bandizip 是一款压缩软件,它支持Zip、7-Zip 和 RAR 以及其它压缩格式。它拥有非…...
LiveCharts2 初步认识
文章目录 1 LiveCharts2 是什么?2 LiveCharts2 可以做什么?3 简单使用LiveCharts2 ,实现动态曲线图 1 LiveCharts2 是什么? GitHub:https://github.com/beto-rodriguez/LiveCharts2 官网: https://lvchar…...
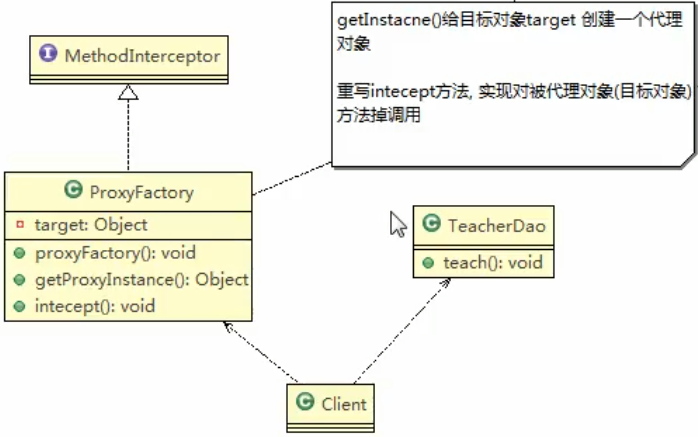
Java设计模式 11-代理模式
代理模式 一、 代理模式(Proxy) 1、代理模式的基本介绍 代理模式:为一个对象提供一个替身,以控制对这个对象的访问。即通过代理对象访问目标对象.这样做的好处是: 可以在目标对象实现的基础上,增强额外的功能操作,即扩展目标对象的功能。被代理的对象…...
Python综合案例-小费数据集的数据分析(详细思路+源码解析)
目录 1. 请导入相应模块并获取数据。导入待处理数据tips.xls,并显示前5行。 2、分析数据 3.增加一列“人均消费” 4查询抽烟男性中人均消费大于5的数据 5.分析小费金额和消费总额的关系,小费金额与消费总额是否存在正相关关系。画图观察。 6分析男女顾…...

软件安全测试
软件安全性测试包括程序、网络、数据库安全性测试。根据系统安全指标不同测试策略也不同。 1.用户程序安全的测试要考虑问题包括: ① 明确区分系统中不同用户权限; ② 系统中会不会出现用户冲突; ③ 系统会不会因用户的权限的改变造成混乱; ④ 用户登陆密码是否…...
Scala模式匹配
Scala中有一个非常强大的模式匹配机制,应用也非常广泛, 例如: 判断固定值 类型查询 快速获取数据 简单模式匹配 一个模式匹配包含了一系列备选项,每个备选项都开始于关键字 case。且每个备选项都包含了一个模式及一到多个表达式。箭头符号 > 隔开…...

银行数仓分层架构
一、为什么要对数仓分层 实现好分层架构,有以下好处: 1清晰数据结构: 每一个数据分层都有对应的作用域,在使用数据的时候能更方便的定位和理解。 2数据血缘追踪: 提供给业务人员或下游系统的数据服务时都是目标数据&…...

Go并发编程的学习代码示例:生产者消费者模型
文章目录 前言代码仓库核心概念main.go(有详细注释)结果总结参考资料作者的话 前言 Go并发编程学习的简单代码示例:生产者消费者模型。 代码仓库 yezhening/Programming-examples: 编程实例 (github.com)Programming-examples: 编程实例 (g…...

求a的n次幂
文章目录 求a的n次幂程序设计程序分析求a的n次幂 【问题描述】要求利用书上介绍的从左至右二进制幂算法求a的n次幂; 【输入形式】输入两个正整数,一个是a,一个是n,中间用空格分开 【输出形式】输出一个整数 【样例输入】2 10 【样例输出】1024 【样例输入】3 4 【样例输出】…...

word脚标【格式:第X页(共X页)】
不得不吐槽一下这个论文,真的我好头疼啊。我又菜又不想改。但是还是得爬起来改 (是谁大半夜不能睡觉加班加点改格式啊) 如何插入页码。 格式、要求如下: 操作步骤: ①双击页脚,填好格式,宋体小四和居中都…...
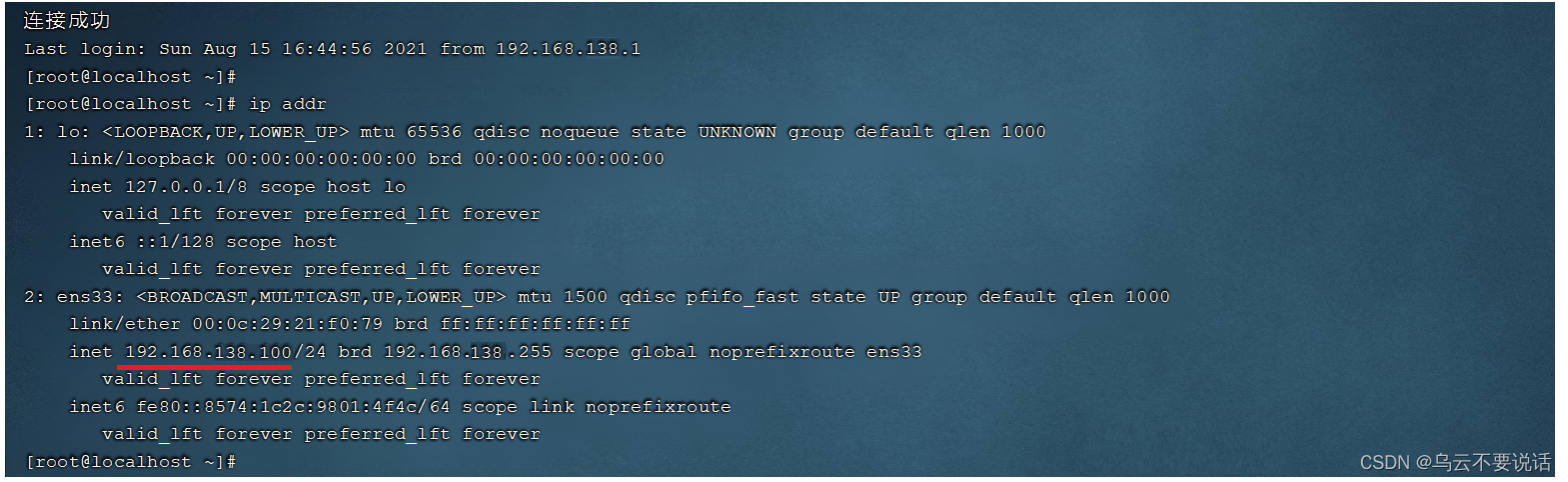
Linux --- 软件安装、项目部署
一、软件安装 1.1、软件安装方式 在Linux系统中,安装软件的方式主要有四种,这四种安装方式的特点如下: 1.2、安装JDK 上述我们介绍了Linux系统软件安装的四种形式,接下来我们就通过第一种(二进制发布包)形式来安装 JDK。 JDK…...

MATLAB应用笔记
其他 1、NaN值 MATLAB判断数据是否为NaN可以直接使用函数:isnan() 三、数据分析 1、相关性 均值、方差、协方差、标准差、相关系数 mean() %均值 nanmean()%去除NAN值求均值 var() %方差 cov() %协方差 std() %标准差 corrcoef(B,b) %R 相关系数plot()…...

ERTEC200P-2 PROFINET设备完全开发手册(6-2)
6.2 诊断与报警实验 首先确认固件为 App1_STANDARD, 将宏定义改为: #define EXAMPL_DEV_CONFIG_VERSION 1 参照第6节的内容,编译和调试固件,并在TIA Portal 中建立RT项目。启动固件后,TIA Portal 切换到在线,可以看…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
