求a的n次幂
相关文章：
求a的n次幂
文章目录 求a的n次幂程序设计程序分析求a的n次幂 【问题描述】要求利用书上介绍的从左至右二进制幂算法求a的n次幂； 【输入形式】输入两个正整数，一个是a，一个是n，中间用空格分开 【输出形式】输出一个整数 【样例输入】2 10 【样例输出】1024 【样例输入】3 4 【样例输出】…...
word脚标【格式：第X页（共X页）】
不得不吐槽一下这个论文，真的我好头疼啊。我又菜又不想改。但是还是得爬起来改 （是谁大半夜不能睡觉加班加点改格式啊） 如何插入页码。 格式、要求如下: 操作步骤： ①双击页脚，填好格式，宋体小四和居中都…...
Linux --- 软件安装、项目部署
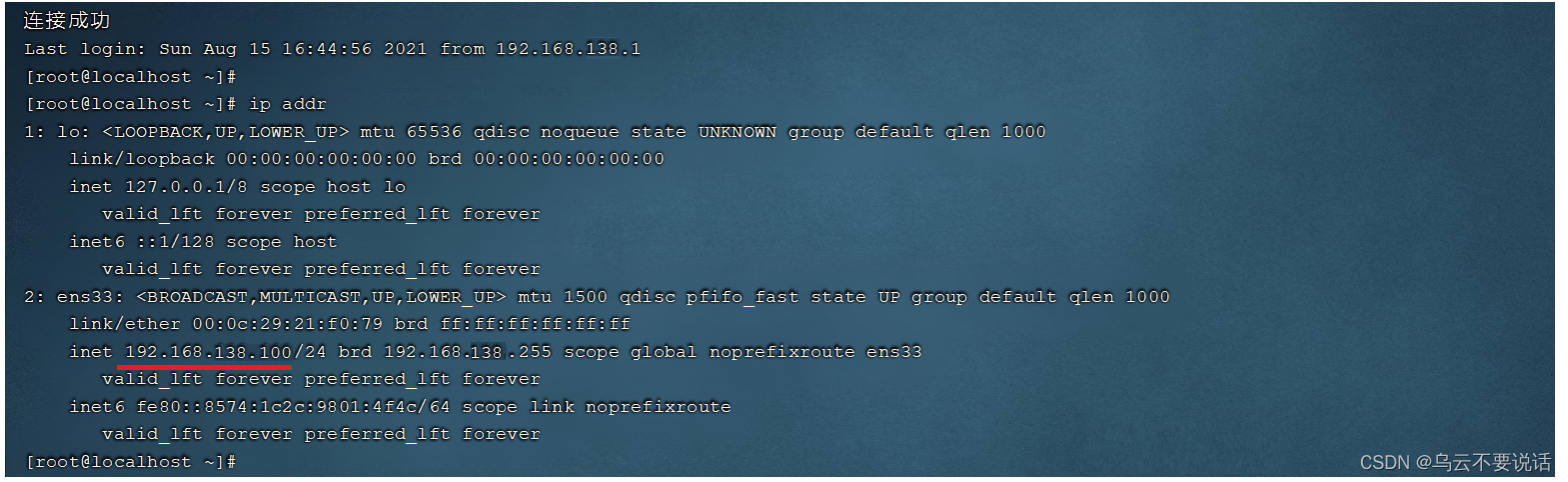
一、软件安装 1.1、软件安装方式 在Linux系统中，安装软件的方式主要有四种，这四种安装方式的特点如下： 1.2、安装JDK 上述我们介绍了Linux系统软件安装的四种形式，接下来我们就通过第一种(二进制发布包)形式来安装 JDK。 JDK…...
MATLAB应用笔记
其他 1、NaN值 MATLAB判断数据是否为NaN可以直接使用函数：isnan() 三、数据分析 1、相关性 均值、方差、协方差、标准差、相关系数 mean() %均值 nanmean()%去除NAN值求均值 var() %方差 cov() %协方差 std() %标准差 corrcoef(B,b) %R 相关系数plot()…...
ERTEC200P-2 PROFINET设备完全开发手册(6-2）
6.2 诊断与报警实验 首先确认固件为 App1_STANDARD, 将宏定义改为： #define EXAMPL_DEV_CONFIG_VERSION 1 参照第6节的内容，编译和调试固件，并在TIA Portal 中建立RT项目。启动固件后，TIA Portal 切换到在线，可以看…...
算法套路八——二叉树深度优先遍历（前、中、后序遍历）
算法套路八——二叉树深度优先遍历（前、中、后序遍历） 算法示例：LeetCode98：验证二叉搜索树 给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下： 节点的左子树只…...
视频批量剪辑：如何给视频添加上下黑边并压缩视频容量。
视频太多了，要如何进行给视频添加上下黑边并压缩视频容量？今天就由小编来教教大家要如何进行操作，感兴趣的小伙伴们可以来看看。 首先，我们要进入视频剪辑高手主页面，并在上方板块栏里选择“批量剪辑视频”板块&#…...
那些你需要知道的互联网广告投放知识
作为一个合格的跨境电商卖家，我们除了有好的产品之外，还要知道怎么去营销我们自己的产品。没有好的推广，即使你的产品有多好别人也是很难看得到的。今天龙哥就打算出一期基础的互联网广告投放科普，希望可以帮到各位增加多一点相关…...
【hello Linux】进程程序替换
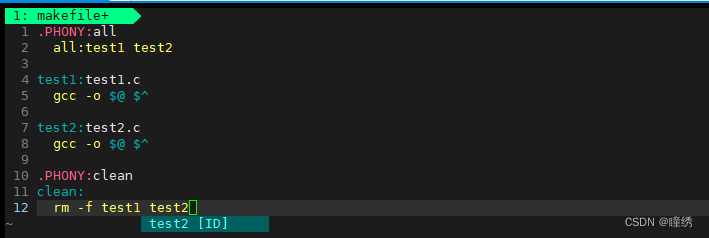
目录 1. 程序替换的原因 2. 程序替换原理 3. 替换函数 4. 函数解释 5. 命名理解 6.简陋版shell的制作 补充： Linux🌷 1. 程序替换的原因 进程自创建后只能执行该进程对应的程序代码，那么我们若想让该进程执行另一个“全新的程序”这 便要用…...
【网络应用开发】实验4——会话管理
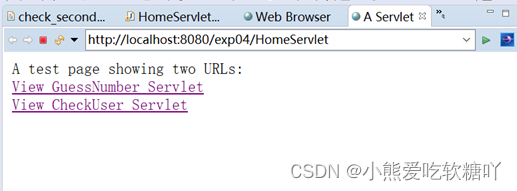
目录 会话管理预习报告 一、实验目的 二、实验原理 三、实验预习内容 1. 什么是会话，一个会话的生产周期从什么时候，到什么时候结束？ 2. 服务器是如何识别管理属于某一个特定客户的会话的？ 3. 什么是Cookie，它的…...
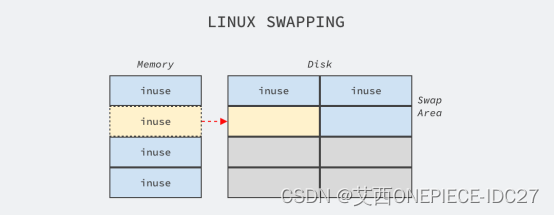
Linux服务器怎么分区
Linux服务器怎么分区 我是艾西，linux系统除了从业某个行业经常要用到的程序员比较熟悉，对于小白或只会用Windows系统的小伙伴还是会比较难上手的。今天艾西简单的跟大家聊聊linux系统怎么分区，让身为小白的你也能一眼看懂直接上手操作感受程序…...
传统机器学习(四)聚类算法DBSCAN
传统机器学习(四)聚类算法DBSCAN 1.1 算法概述 DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇，并在…...
“华为杯”研究生数学建模竞赛2020年-【华为杯】A题：ASIC 芯片上的载波恢复 DSP 算法设计与实现（附获奖论文及matlab代码实现）
目录 摘 要： 1.问题重述 1.1 问题背景 1.2 问题提出 1.3 研究基础 2.模型假设和已知...
1043.分隔数组以得到最大和
题目： 给你一个整数数组 arr，请你将该数组分隔为长度 最多 为 k 的一些（连续）子数组。分隔完成后，每个子数组的中的所有值都会变为该子数组中的最大值。 返回将数组分隔变换后能够得到的元素最大和。本题所用到的测试…...
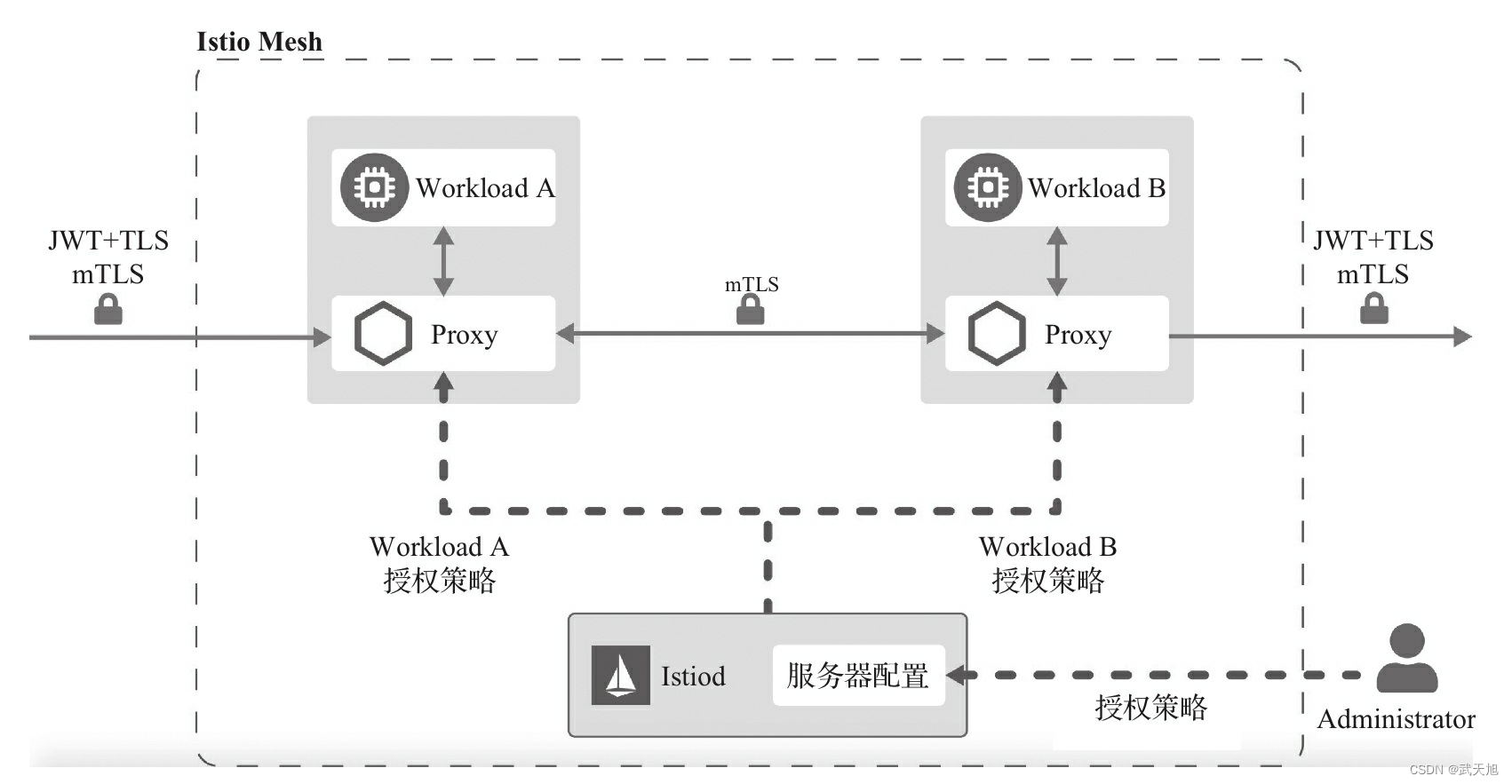
微服务治理框架（Istio）的认证服务与访问控制
本博客地址：https://security.blog.csdn.net/article/details/130152887 一、认证服务 1.1、基于JWT的认证 在微服务架构下，每个服务是无状态的，由于服务端需要存储客户端的登录状态，因此传统的session认证方式在微服务中不再适…...
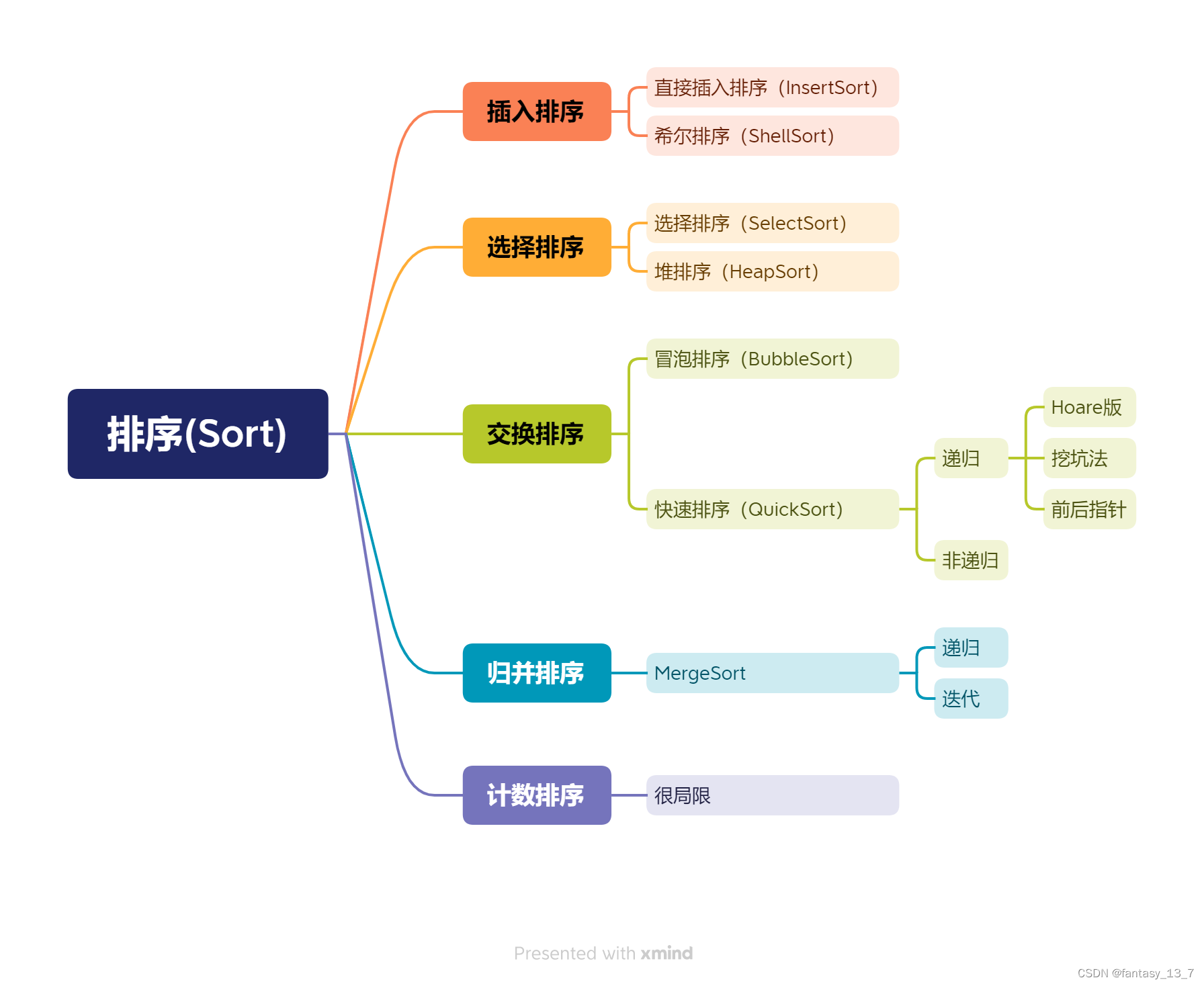
数据结构 | 排序 - 总结
排序的方式 排序的稳定性 什么是排序的稳定性？ 不改变相同数据的相对顺序 排序的稳定性有什么意义？ 假定一个场景： 一组成绩：100，88，98，98，78，100（按交卷顺序…...
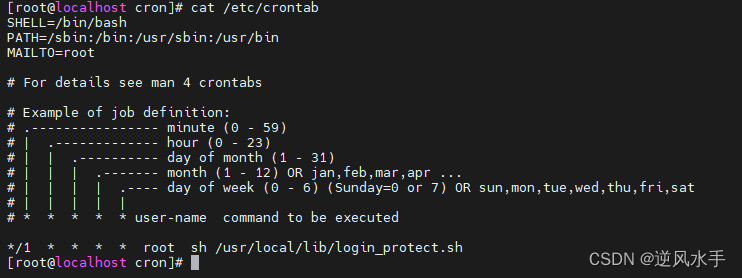
crontab -e 系统定时任务
crontab -e解释 crontab 是由 “cron” 和 “table” 两个单词组成的缩写。其中，“cron” 是一个在 Linux 和类 Unix 操作系统中用于定时执行任务的守护进程，而 “table” 则是指一个表格或者列表，因此 crontab 就是一个用于配置和管理定时任…...
前后端交互系列之Axios详解（包括拦截器）
目录 前言一，服务器的搭建二，Axios的基本使用2.1 Axios的介绍及页面配置2.2 如何安装2.3 Axios的前台代码2.4 Axios的基本使用2.5 axios请求响应结果的结构2.6 带参数的axios请求2.7 axios修改默认配置 三，axios拦截器3.1 什么是拦截器3.2 拦…...
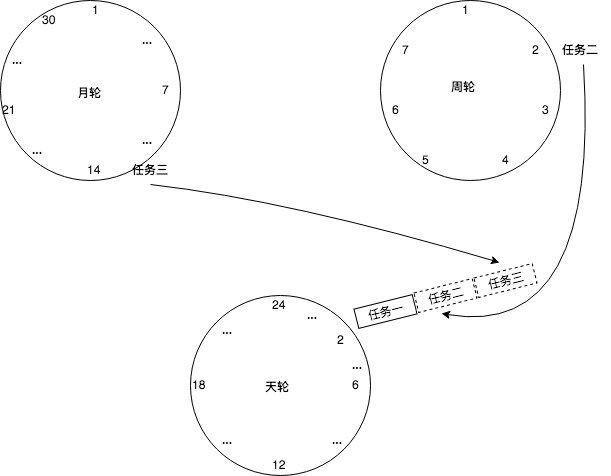
定时任务之时间轮算法
初识时间轮 我们先来考虑一个简单的情况，目前有三个任务A、B、C，分别需要在3点钟，4点钟和9点钟执行，可以把时间想象成一个钟表。 如上图中所示，我只需要把任务放到它需要被执行的时刻，然后等着时针转到这个…...
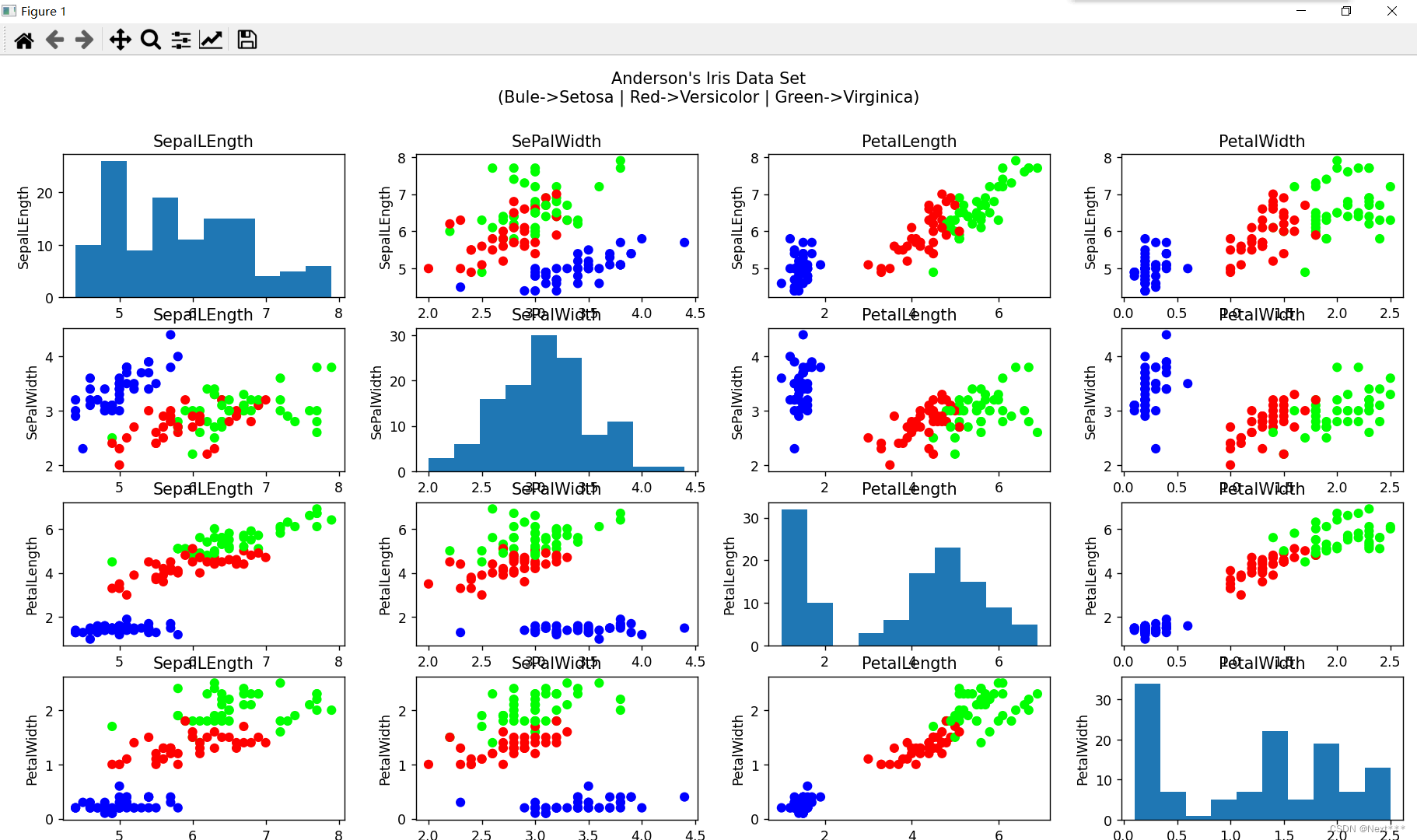
实验4 Matplotlib数据可视化
1. 实验目的 ①掌握Matplotlib绘图基础； ②运用Matplotlib，实现数据集的可视化； ③运用Pandas访问csv数据集。 2. 实验内容 ①绘制散点图、直方图和折线图，对数据进行可视化； ②下载波士顿数房价据集，并…...
基于OpenStack的毕业设计：从零搭建私有云平台的入门实战与避坑指南
最近在帮学弟学妹们看毕业设计，发现不少同学对云计算方向很感兴趣，尤其是想用OpenStack做个私有云平台。但一上手就懵了，组件多、文档杂，环境动不动就崩，最后时间都花在折腾部署上了。我自己当初也踩过不少坑ÿ…...
单阶段检测的王者：YOLO核心技术解析与多场景应用实战指南
导读：在计算机视觉的浩瀚星空中，YOLO (You Only Look Once) 无疑是最耀眼的那颗星。自2015年横空出世以来，它凭借“单阶段检测”的独特哲学，将速度与精度完美统一，彻底终结了Two-Stage算法在实时领域的统治地位。站在2…...
ElasticJob HTTP作业：RESTful接口调度的终极指南
ElasticJob HTTP作业：RESTful接口调度的终极指南 ElasticJob是ShardingSphere生态中一款分布式任务调度解决方案，它提供了丰富的作业类型支持，其中HTTP作业是实现跨系统任务调度的理想选择。通过HTTP作业，您可以轻松实现基于REST…...
OpenClaw+百川2-13B量化模型：自动化技术文档摘要系统搭建
OpenClaw百川2-13B量化模型：自动化技术文档摘要系统搭建 1. 为什么需要自动化文档摘要系统 作为一个经常需要阅读大量技术文档的开发者，我发现自己陷入了"文档海洋"的困境。每次研究新技术时，总会下载几十份PDF白皮书、API文档和…...
嵌入式NMEA-0183零内存分配解析器设计与实现
1. NMEA-0183 协议解析库深度技术解析：面向嵌入式系统的轻量级、零内存分配实现 NMEA-0183（National Marine Electronics Association 0183）是全球航海电子设备事实上的标准通信协议，自1983年发布以来，已广泛应用于GPS…...
EzArduino：面向初学者的Arduino面向对象封装库
1. EzArduino 库概述：面向嵌入式初学者的面向对象 Arduino 抽象层EzArduino 是一个专为 Arduino 平台设计的轻量级 C 封装库，其核心目标是降低硬件交互门槛、提升代码可读性与可维护性。它并非替代 Arduino Core 的底层实现，而是在Arduino.h基…...
CAN总线故障诊断与维修全指南
经典CAN总线现场故障分析与诊断指南1. CAN总线故障概述1.1 常见故障现象当CAN总线系统出现传输异常时，通常会表现为多种复合故障现象，包括但不限于：仪表板显示异常车辆启动/熄火功能失效动力系统性能下降特定电控模块功能丧失这些现象的根本原…...
VMware macOS支持解锁创新解决方案
VMware macOS支持解锁创新解决方案 【免费下载链接】unlocker 项目地址: https://gitcode.com/gh_mirrors/unloc/unlocker 在虚拟化技术广泛应用的今天，VMware作为行业领先的虚拟化平台，却默认隐藏了对macOS操作系统的支持选项。这种商业策略导致…...
关于前端获取DOM节点的兼容IE6的代码封装
返回所有子元素节点的代码封装// 封装一个函数，这个函数可以返回元素的所有子元素节点(兼容到IE6)，类似children的功能function getChildren(node){// 结果数组var children [];// 遍历node这个节点的所有子节点，判断每一个子节点的nodeType…...
电源防反接电路设计与实现方案
电源防反接电路的工程实现方案1. 电源防反接技术背景在工业控制和自动化设备中，电源接线错误是常见的操作失误。当电源极性接反时，轻则导致设备无法工作，重则烧毁关键元器件。传统的保险丝保护方案存在响应速度慢、需要人工更换等缺点&#x…...