算法套路八——二叉树深度优先遍历(前、中、后序遍历)
算法套路八——二叉树深度优先遍历(前、中、后序遍历)
算法示例:LeetCode98:验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
方法一:前序遍历——先判断,再递归
前序遍历即先遍历根节点,再遍历左右子树
前序遍历我们的思路是先判断当前结点是否满足二叉搜索树的条件,再递归左右子树。
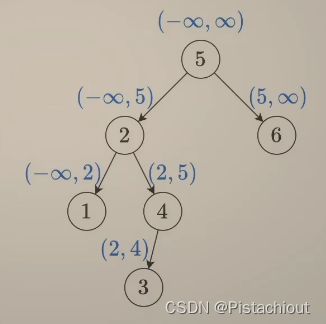
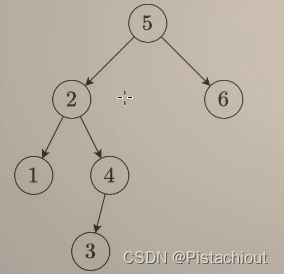
且如上图所示,在二叉搜索树中,使用前序遍历时有如上的规律,从根节点传递取值范围,对于任意一个结点,其取值范围已经确定,若结点值不在范围内,则不是二叉搜索树。
步骤如下所示:
- root结点的取值范围为(-inf,+inf),判断是否满足条件
- 判断左子树是否是二叉搜索树,且此时最大值应该小于root.val,所以取值范围为(-inf,root.val]
- 判断右子树是否是二叉搜索树,且此时最小值应该大于root.val,所以取值范围为[root.val,inf)
- 对于2,3采取递归遍历
且注意判断root是否为空
class Solution:def isValidBST(self, root: Optional[TreeNode], left=-inf, right=inf) -> bool:if root is None:return Truex = root.valreturn left < x < right and \self.isValidBST(root.left, left, x) and \self.isValidBST(root.right, x, right)
方法二:中序遍历——先判断,再递归
中序遍历即先遍历左节点、根节点,最后遍历右节点
且中序遍历下二叉搜索树应该为递增数组,所以我们直接判断当前节点值是否大于上一个遍历的节点值pre
其实这也等价于约束节点的范围,在中序遍历时只需要修改最小值,即取值范围是(pre,inf)
- 判断左子树是否是二叉搜索树,且记录左子树最后一个被遍历的节点值为pre,也是左子树的最大值
- 比较当前节点指是否大于pre,即取值范围是(pre,inf),
- 判断右子树是否是二叉搜索树
- 对于1,3采取递归遍历
class Solution:pre = -infdef isValidBST(self, root: Optional[TreeNode]) -> bool:if root is None:return Trueif not self.isValidBST(root.left):return Falseif root.val<=self.pre:return Falseself.pre = root.valreturn self.isValidBST(root.right)方法三:后序遍历——先递归,在判断
后序遍历即先遍历左节点、右节点,最后遍历根节点
后序遍历也可以传递节点的范围,不过是从叶子节点向根节点传递,根节点需要大于左子树的最大值,小于右子树的最小值。
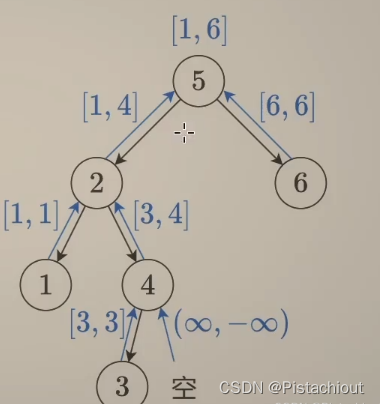
- 如果当今节点为null空节点,则返回(inf,-inf),因为任何值都会小于inf,任何值都会大于-inf,这样就不会影响到树的最大最小值的取值,可以仔细体会。
- 遍历左子树,且返回左子树的最小值l_min与最大值l_max
- 遍历右子树,且返回右子树的最小值r_min与最大值r_max
- 比较当前节点的值,若取值位于(l_max ,r_min),则更新最小值与最大值并返回即min(l_min, x), max(r_max, x)。若取值不在范围内,则表示不是二叉搜索树,此时我们返回正常情况不会返回的(-inf,inf)来表示False
- 比较返回值是否是正常值,这等价与判断是否等于inf无穷即非正常值,若等于inf则返回False,若不等于inf则返回True
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:def dfs(node: Optional[TreeNode]) -> Tuple:if node is None:return inf, -infl_min, l_max = dfs(node.left)r_min, r_max = dfs(node.right)x = node.val# 也可以在递归完左子树之后立刻判断,如果不是二叉搜索树,就不用递归右子树了if x <= l_max or x >= r_min:return -inf, inf#返回无穷表示为False,不满足搜索树return min(l_min, x), max(r_max, x)return dfs(root)[1] != inf
总结:
前序遍历在某些数据下不需要递归到边界(base case)就能返回,而另外两种需要递归到至少一个边界,从这个角度上来说它是最快的。
中序遍历很好地利用到了二叉搜索树的性质,使用到的变量最少。
后序遍历的思想是最通用的,即自底向上计算子问题的过程。想要学好动态规划的话,请务必掌握这个思想。
且由以上示例代码都可以看出,在代码书写时要定义内部匿名函数dfs,不然可能会由于LeetCode判断问题影响结果
算法练习一:LeetCode230. 二叉搜索树中第K小的元素
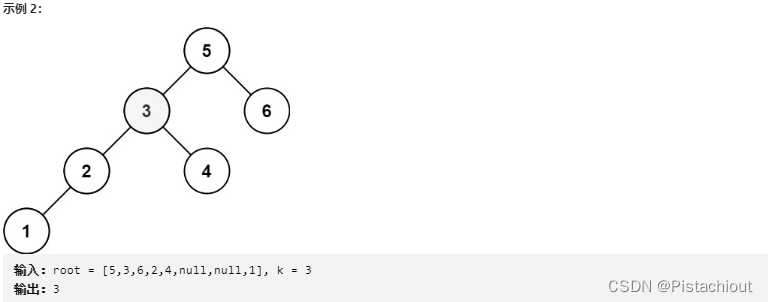
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历,每次遍历时k–,当k为0时则表示当前结点为第k个结点,则令ans等于该值
func kthSmallest(root *TreeNode, k int) int {var ans intvar dfs func(node *TreeNode) dfs=func(node *TreeNode) {if node==nil{return }dfs(node.Left)k--if k==0{ans=node.Val}dfs(node.Right)}dfs(root)return ans
}
算法练习二:LeetCode501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。
利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历,将遍历节点与前一个节点比较,然后使用变量cur,max来记录当前节点与最多节点,且注意要定义匿名函数解决。
func findMode(root *TreeNode) []int {var (ans []intpre, cur, max intdfs func(*TreeNode))dfs = func(node *TreeNode) {if node == nil {return}dfs(node.Left)if node.Val == pre {cur++} else {cur = 1}if cur > max {max = curans = []int{node.Val}} else if cur == max {ans = append(ans, node.Val)}pre = node.Valdfs(node.Right)}dfs(root)return ans
}
算法练习三:LeetCode530. 二叉搜索树的最小绝对差
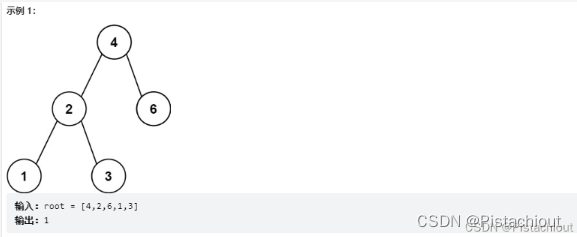
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。差值是一个正数,其数值等于两值之差的绝对值。
利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历,将遍历节点与前一个节点比较,然后使用变量pre,min来记录前一个结点节点值与当前最小差值,并定义匿名函数解决。
func getMinimumDifference(root *TreeNode) int {min, pre := math.MaxInt64, -1var dfs func(node *TreeNode)dfs=func(node *TreeNode){if node==nil{return }dfs(node.Left)sub:=node.Val-preif sub<min&&pre!=-1{min=sub}pre=node.Valdfs(node.Right)
}dfs(root)return min
}
算法练习四:LeetCode700. 二叉搜索树中的搜索
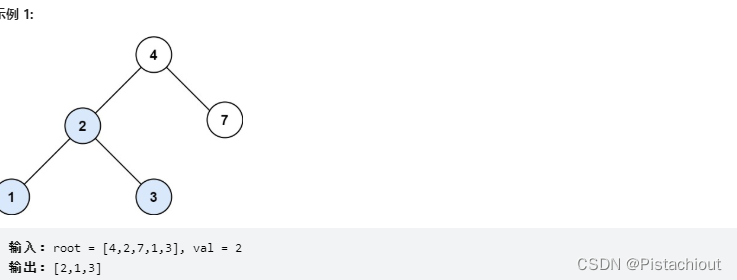
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null。
若 root 为空则返回空节点;
若 val=root.val,则返回 \textit{root}root;
若val<root.val,递归左子树;
若 val>root.val,递归右子树。
func searchBST(root *TreeNode, val int) *TreeNode {if root == nil {return nil}if val == root.Val {return root}if val < root.Val {return searchBST(root.Left, val)}return searchBST(root.Right, val)
}
算法进阶一:LeetCode236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
本题可以使用分类讨论,如下图所示,定义函数dfs()返回当前结点node的子树是否找到p或q,有以下情况

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {return dfs(root,p,q)
}
func dfs(node, p, q *TreeNode) *TreeNode{if node == nil || node == p || node == q {return node}left := dfs(node.Left, p, q)right := dfs(node.Right, p, q)if left != nil && right != nil {return node}if left != nil {return left}return right
}
算法进阶二:LeetCode236. 二叉树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
本题与上题一样,只不过在判断p,q的位置时可以利用线索二叉树值的大小性质来判断

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {return dfs(root,p,q)
}
func dfs(node, p, q *TreeNode) *TreeNode{if node == nil || node == p || node == q {return node}if node.Val>p.Val&&node.Val>q.Val{return dfs(node.Left,p,q)}else if node.Val<p.Val&&node.Val<q.Val{return dfs(node.Right,p,q)}return node
}
相关文章:

算法套路八——二叉树深度优先遍历(前、中、后序遍历)
算法套路八——二叉树深度优先遍历(前、中、后序遍历) 算法示例:LeetCode98:验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只…...
视频批量剪辑:如何给视频添加上下黑边并压缩视频容量。
视频太多了,要如何进行给视频添加上下黑边并压缩视频容量?今天就由小编来教教大家要如何进行操作,感兴趣的小伙伴们可以来看看。 首先,我们要进入视频剪辑高手主页面,并在上方板块栏里选择“批量剪辑视频”板块&#…...

那些你需要知道的互联网广告投放知识
作为一个合格的跨境电商卖家,我们除了有好的产品之外,还要知道怎么去营销我们自己的产品。没有好的推广,即使你的产品有多好别人也是很难看得到的。今天龙哥就打算出一期基础的互联网广告投放科普,希望可以帮到各位增加多一点相关…...
【hello Linux】进程程序替换
目录 1. 程序替换的原因 2. 程序替换原理 3. 替换函数 4. 函数解释 5. 命名理解 6.简陋版shell的制作 补充: Linux🌷 1. 程序替换的原因 进程自创建后只能执行该进程对应的程序代码,那么我们若想让该进程执行另一个“全新的程序”这 便要用…...
【网络应用开发】实验4——会话管理
目录 会话管理预习报告 一、实验目的 二、实验原理 三、实验预习内容 1. 什么是会话,一个会话的生产周期从什么时候,到什么时候结束? 2. 服务器是如何识别管理属于某一个特定客户的会话的? 3. 什么是Cookie,它的…...
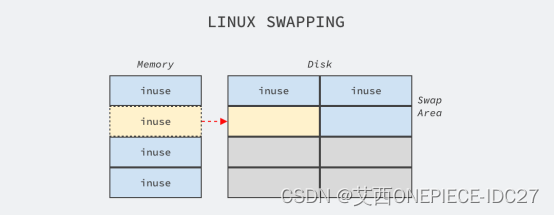
Linux服务器怎么分区
Linux服务器怎么分区 我是艾西,linux系统除了从业某个行业经常要用到的程序员比较熟悉,对于小白或只会用Windows系统的小伙伴还是会比较难上手的。今天艾西简单的跟大家聊聊linux系统怎么分区,让身为小白的你也能一眼看懂直接上手操作感受程序…...

传统机器学习(四)聚类算法DBSCAN
传统机器学习(四)聚类算法DBSCAN 1.1 算法概述 DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇,并在…...
)
“华为杯”研究生数学建模竞赛2020年-【华为杯】A题:ASIC 芯片上的载波恢复 DSP 算法设计与实现(附获奖论文及matlab代码实现)
目录 摘 要: 1.问题重述 1.1 问题背景 1.2 问题提出 1.3 研究基础 2.模型假设和已知...

1043.分隔数组以得到最大和
题目: 给你一个整数数组 arr,请你将该数组分隔为长度 最多 为 k 的一些(连续)子数组。分隔完成后,每个子数组的中的所有值都会变为该子数组中的最大值。 返回将数组分隔变换后能够得到的元素最大和。本题所用到的测试…...
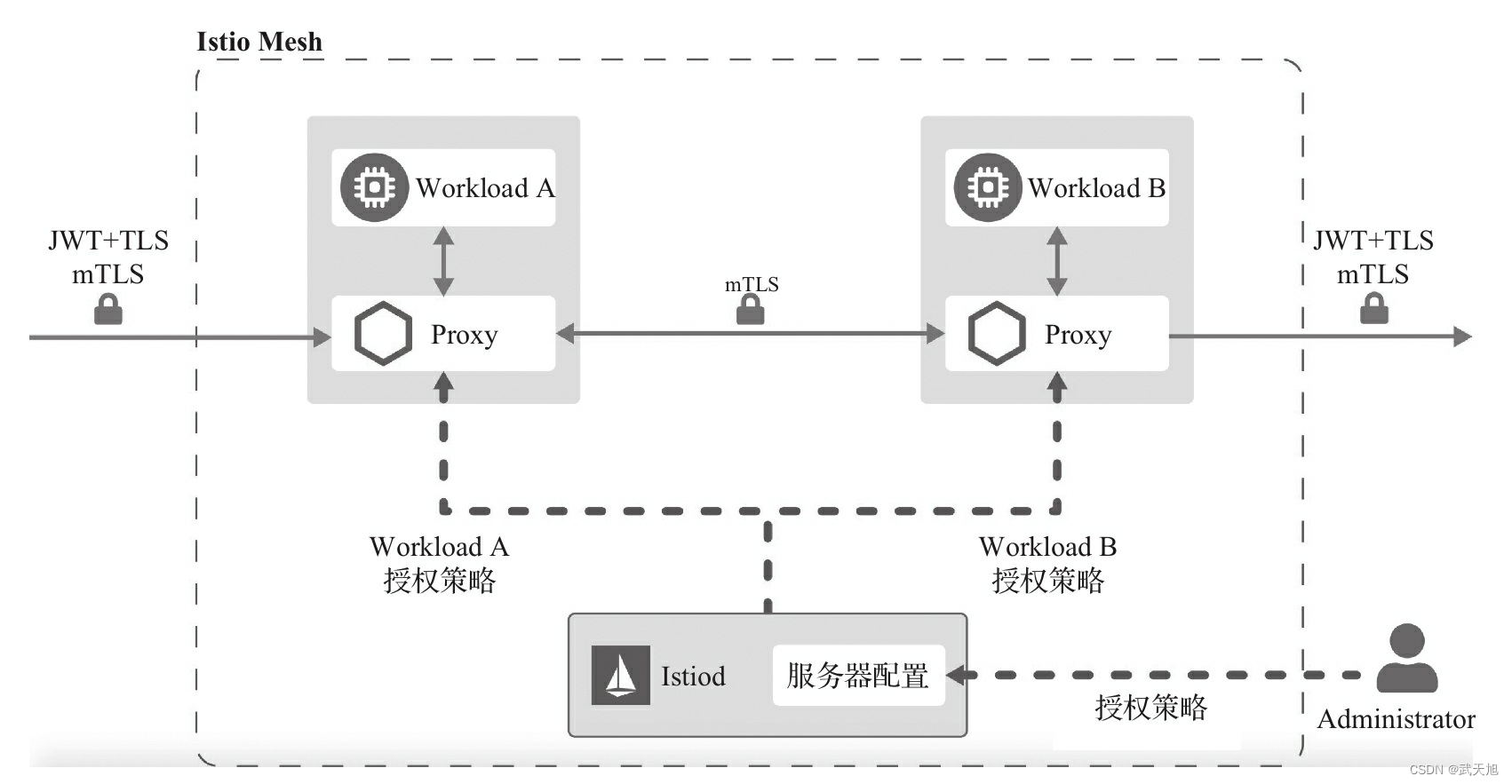
微服务治理框架(Istio)的认证服务与访问控制
本博客地址:https://security.blog.csdn.net/article/details/130152887 一、认证服务 1.1、基于JWT的认证 在微服务架构下,每个服务是无状态的,由于服务端需要存储客户端的登录状态,因此传统的session认证方式在微服务中不再适…...
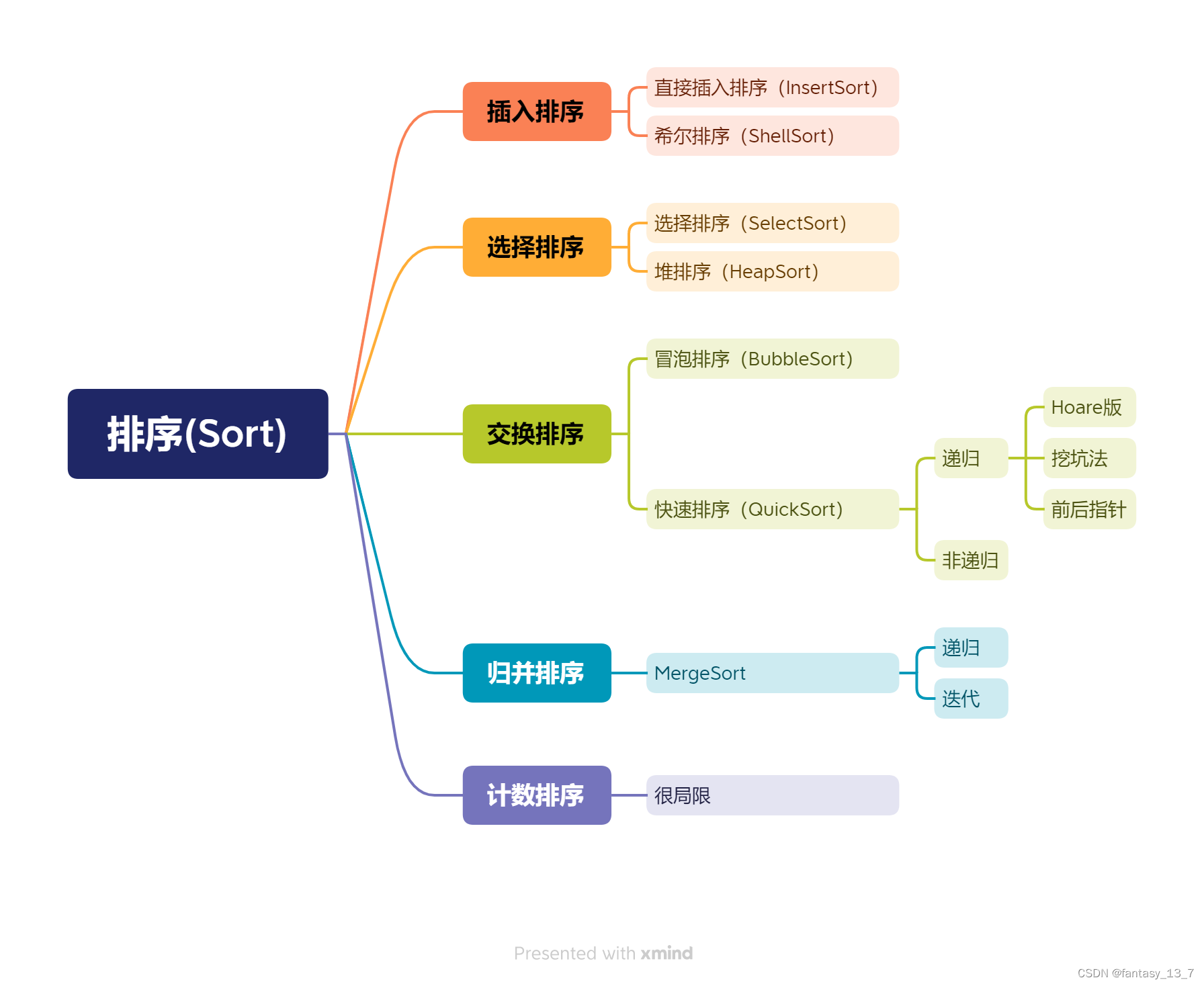
数据结构 | 排序 - 总结
排序的方式 排序的稳定性 什么是排序的稳定性? 不改变相同数据的相对顺序 排序的稳定性有什么意义? 假定一个场景: 一组成绩:100,88,98,98,78,100(按交卷顺序…...
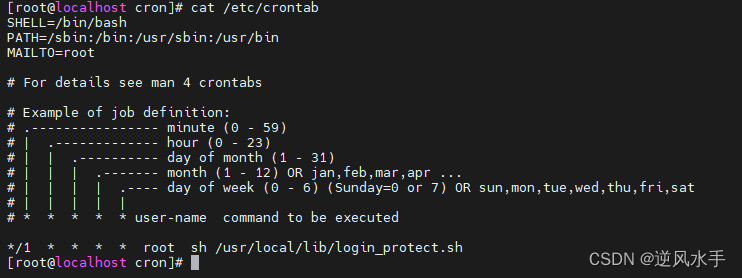
crontab -e 系统定时任务
crontab -e解释 crontab 是由 “cron” 和 “table” 两个单词组成的缩写。其中,“cron” 是一个在 Linux 和类 Unix 操作系统中用于定时执行任务的守护进程,而 “table” 则是指一个表格或者列表,因此 crontab 就是一个用于配置和管理定时任…...
前后端交互系列之Axios详解(包括拦截器)
目录 前言一,服务器的搭建二,Axios的基本使用2.1 Axios的介绍及页面配置2.2 如何安装2.3 Axios的前台代码2.4 Axios的基本使用2.5 axios请求响应结果的结构2.6 带参数的axios请求2.7 axios修改默认配置 三,axios拦截器3.1 什么是拦截器3.2 拦…...
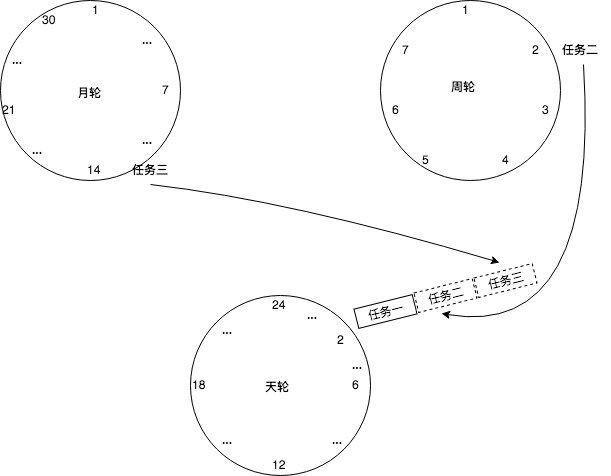
定时任务之时间轮算法
初识时间轮 我们先来考虑一个简单的情况,目前有三个任务A、B、C,分别需要在3点钟,4点钟和9点钟执行,可以把时间想象成一个钟表。 如上图中所示,我只需要把任务放到它需要被执行的时刻,然后等着时针转到这个…...
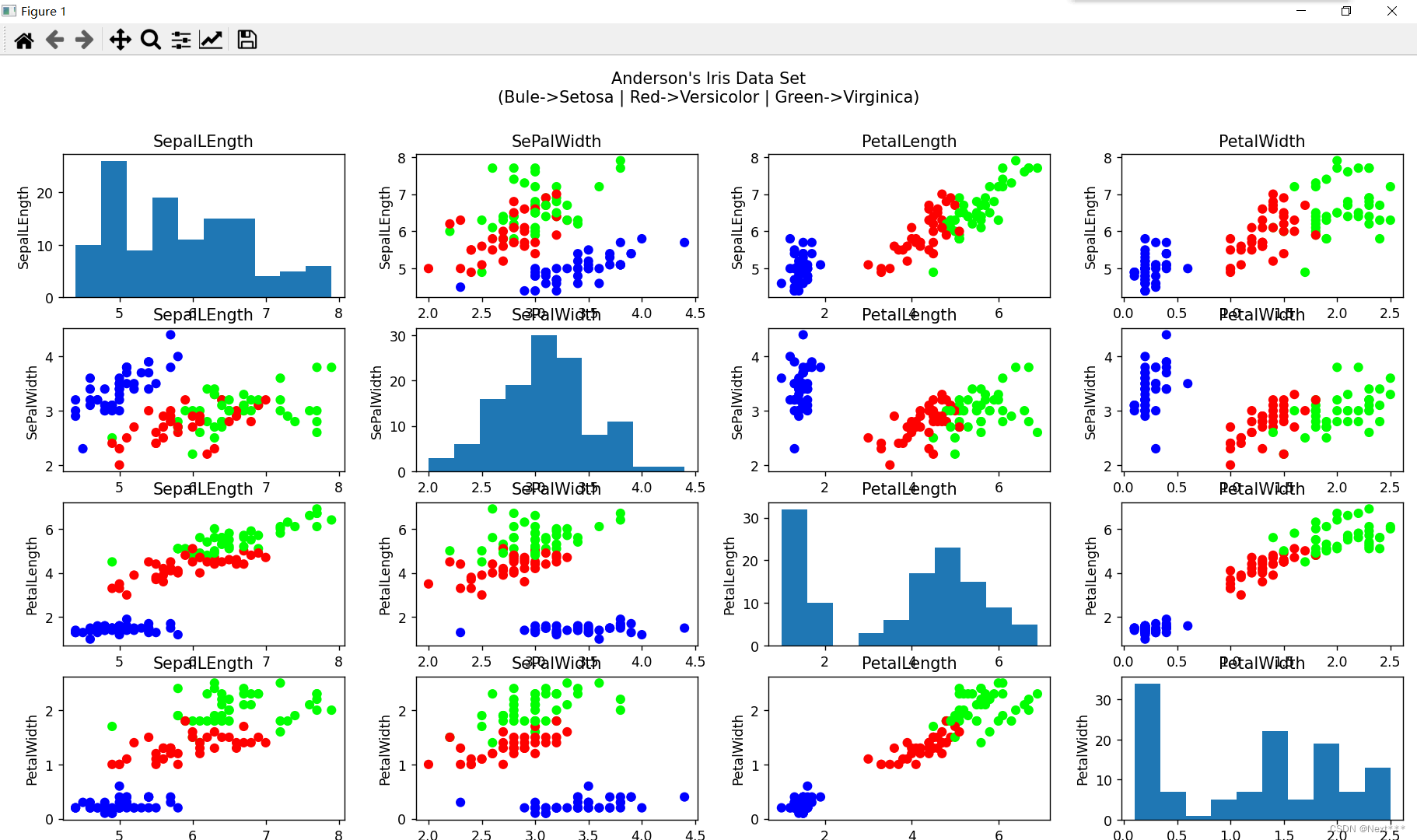
实验4 Matplotlib数据可视化
1. 实验目的 ①掌握Matplotlib绘图基础; ②运用Matplotlib,实现数据集的可视化; ③运用Pandas访问csv数据集。 2. 实验内容 ①绘制散点图、直方图和折线图,对数据进行可视化; ②下载波士顿数房价据集,并…...

【软件工程】为什么要选择软件工程专业?
个人主页:【😊个人主页】 文章目录 前言软件工程💻💻💻就业岗位👨💻👨💻👨💻就业前景🛩️🛩️🛩️工作环…...

5类“计算机”专业很吃香,人才缺口巨大,就业前景良好
说到目前最热门的专业,计算机绝对占有一席之地,是公认的发展前景好、人才缺口大的专业。有人称该专业人数如此众多,势必会导致人才饱和,但是从当前社会互联网发展的趋势来看,计算机专业在很长一段时间都是发展很好的专…...

数仓选型对比
1、数仓选型对比如下(先列举表格,后续逐个介绍) 数仓应用目标产品特点适用于 适用数据类型数据处理速度性能拓展 实施难度运维难度性能优化成本传统数仓(SQLServer、Oracle等关系型数据库)面向主题设计的,为 分析数据而设计基于Oracle、 SQLServer、MyS…...
Java详解与代码实现)
二叉树的遍历(前序、中序、后序)Java详解与代码实现
递归遍历 前序,中序,后序 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, Tree…...

如何找出消耗CPU最多的线程?
如何找出消耗CPU最多的线程? 1.使用 top -c 找出所有当前进程的运行列表 top -c 2.按P(Shiftp)对所有进程按CPU使用率进行排序,找出消耗最高的线程PID 显示Java进程 PID 为 136 的java进程消耗最 3.使用 top -Hp PID,查出里面消…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...