1043.分隔数组以得到最大和
题目:
给你一个整数数组 arr,请你将该数组分隔为长度 最多 为 k 的一些(连续)子数组。分隔完成后,每个子数组的中的所有值都会变为该子数组中的最大值。
返回将数组分隔变换后能够得到的元素最大和。本题所用到的测试用例会确保答案是一个 32 位整数。
示例 1:
输入:arr = [1,15,7,9,2,5,10], k = 3
输出:84
解释:数组变为 [15,15,15,9,10,10,10]
示例 2:
输入:arr = [1,4,1,5,7,3,6,1,9,9,3], k = 4
输出:83
示例 3:
输入:arr = [1], k = 1
输出:1
提示:
1 <= arr.length <= 500
0 <= arr[i] <= 109
1 <= k <= arr.length
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/partition-array-for-maximum-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
首先要看样例来寻找灵感。
在推完前两个样例的时候,应该就会发现规律。当你从前往后开始进行的时候,每到一个位置都要进行判断,是不是要以当前位置为核心开始赋值,如果是最大值要向周围进行赋值的话,是先前还是先后,分别向前多少向后多少,这些都是你要考虑的。
就以第二个例子为例,i 从0到n-1开始进行判断:
i =0的时候那肯定是1 ;、
i =1的时候,发现4是向前k个数里最大的,因此此时的最大值是4 , 整体的和就是8 ;
i = 2的时候,发现k 个数内还是4是最大值,因此整体的和就是12 ;
i = 3 的时候,发现 k 个数内最大值是5 , 因此整体的和就是20;
i = 4 的时候,发现 k 个数内最大值是7 , 但是k=4,所以最多只能向前赋值4个数,和就是29;
…
好的,推到这里,应该就有感觉了吧?
没有!?那我让你有点感觉~
你会发现,i 从前向后走的时候,每走到一个新的值,那以i 结尾的整体的和的最大值其实就是可以得到的,也就是说当前位置的最终答案是可以根据之前得到的结果计算得到,都说到这了还没有感觉么?
这不就是状态转移方程嘛!这不就是DP的感觉嘛!
用dp【i】 来表示以 i 作为结尾元素的整体的最大和,最后的答案就是dp【n-1】。
那状态转移方程就可以是:
dp【i】 = max(dp【i】,( j >0 ? dp[j-1] : 0) + res*(i-j+1))
j 的含义是从 i 开始向前枚举 k 个位置 , 以为之前的每个位置的整体最大和是已经算过的,也就是dp【0】到dp【i-1】都是计算过的,那 j 从 i 开始向前枚举,用arr【j】来更新 j 到 i 内的最大值res,然后将res赋值到 j 到 i 的所有数,dp【i】就取赋值之前和赋值之后的较大值。
通过这样的状态转移方程,i 从 0 遍历到 n-1 , 最终的dp【n-1】就是要返回的答案!
代码:
class Solution {
public:int maxSumAfterPartitioning(vector<int>& arr, int k) {int n = arr.size();int dp[510] = {0};for(int i = 0 ; i < n ; i++){int res = arr[i];for(int j = i ; j >= max(i-k+1 , 0) ; j--){res = max(res , arr[j]);dp[i] = max(dp[i] , (j > 0 ? dp[j-1] : 0) + res*(i-j+1));// cout << i << " " << j << " " << res << endl;// cout << dp[i] << endl;}}return dp[n-1];}
};相关文章:

1043.分隔数组以得到最大和
题目: 给你一个整数数组 arr,请你将该数组分隔为长度 最多 为 k 的一些(连续)子数组。分隔完成后,每个子数组的中的所有值都会变为该子数组中的最大值。 返回将数组分隔变换后能够得到的元素最大和。本题所用到的测试…...
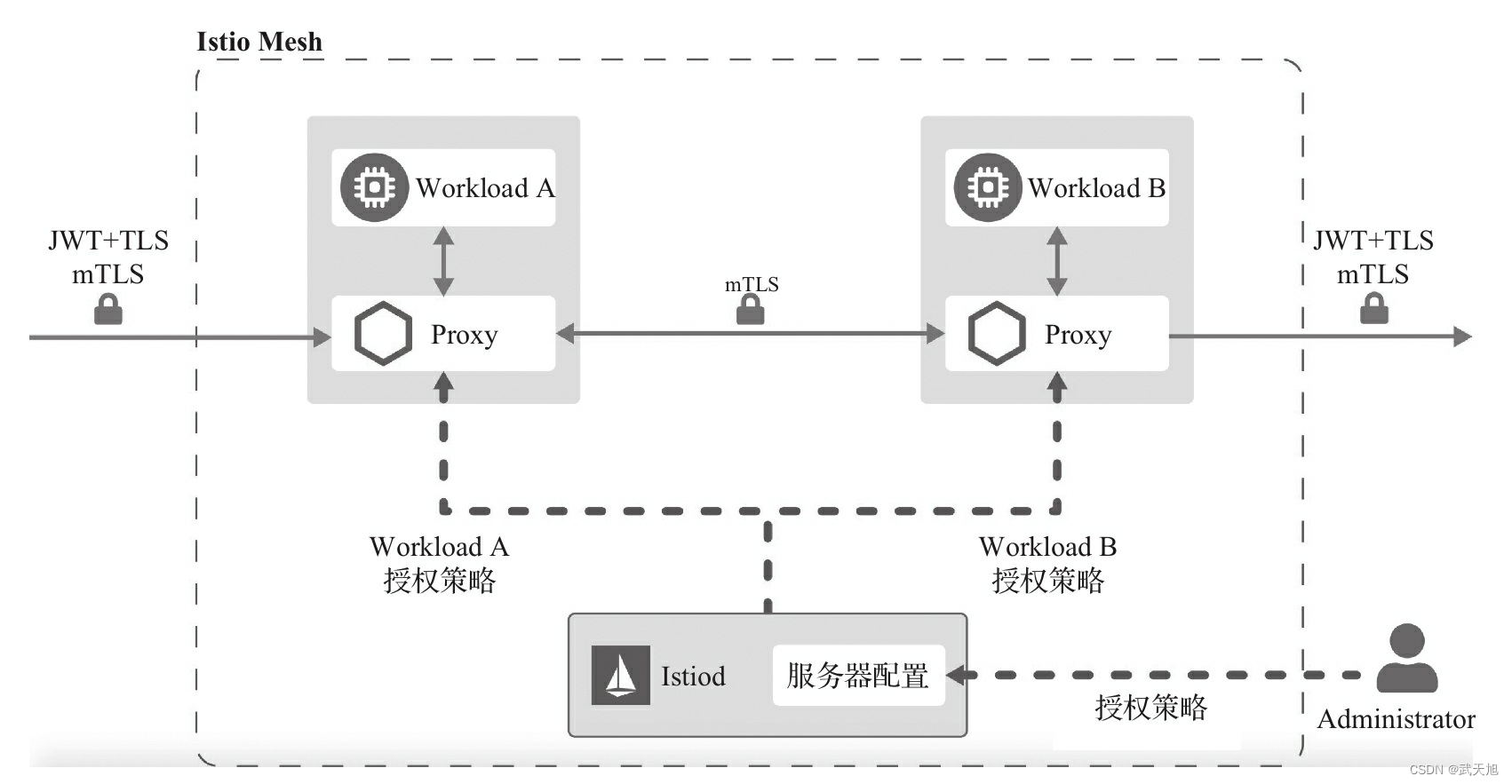
微服务治理框架(Istio)的认证服务与访问控制
本博客地址:https://security.blog.csdn.net/article/details/130152887 一、认证服务 1.1、基于JWT的认证 在微服务架构下,每个服务是无状态的,由于服务端需要存储客户端的登录状态,因此传统的session认证方式在微服务中不再适…...
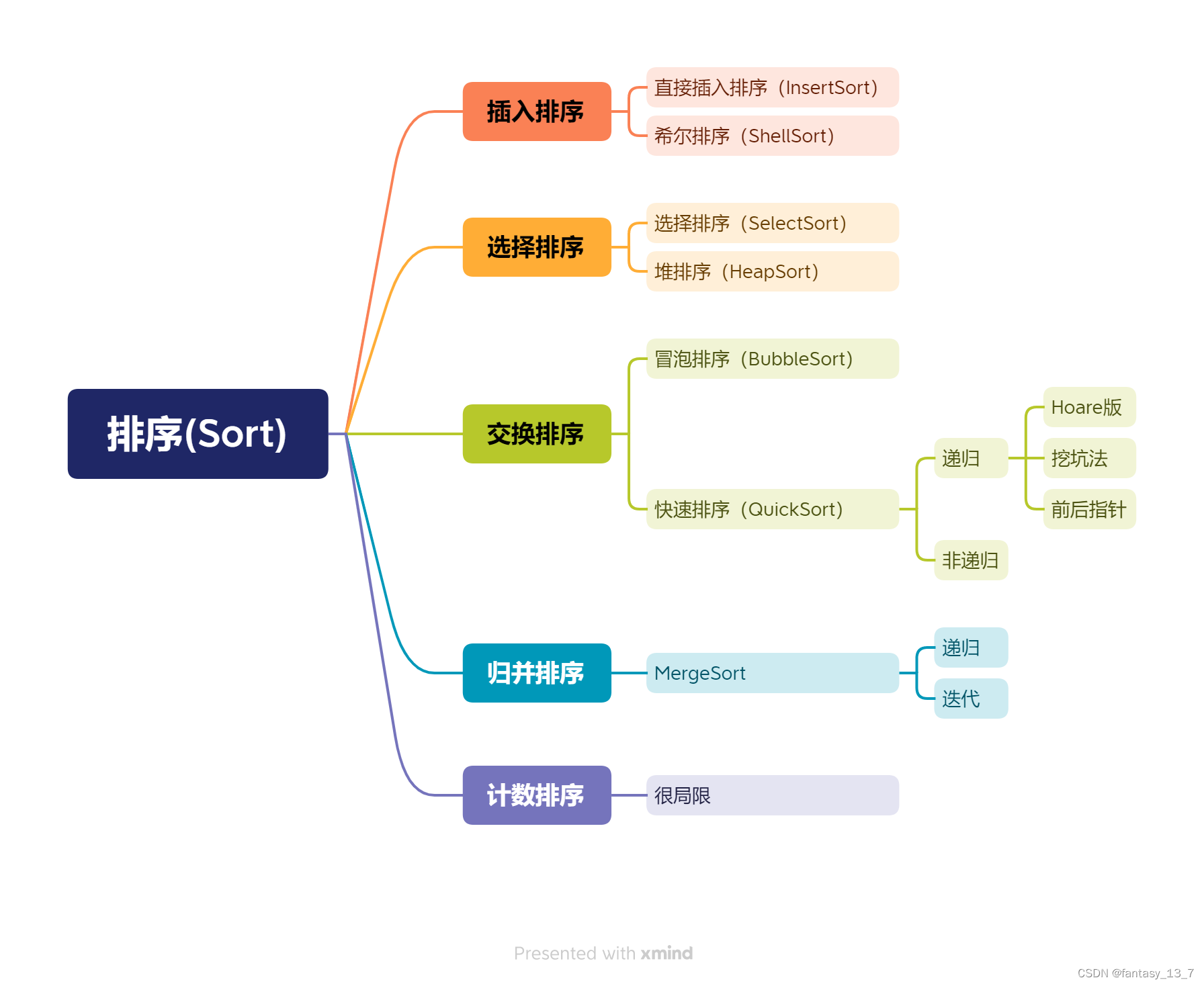
数据结构 | 排序 - 总结
排序的方式 排序的稳定性 什么是排序的稳定性? 不改变相同数据的相对顺序 排序的稳定性有什么意义? 假定一个场景: 一组成绩:100,88,98,98,78,100(按交卷顺序…...
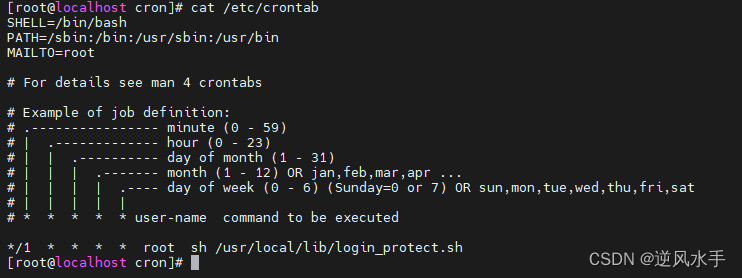
crontab -e 系统定时任务
crontab -e解释 crontab 是由 “cron” 和 “table” 两个单词组成的缩写。其中,“cron” 是一个在 Linux 和类 Unix 操作系统中用于定时执行任务的守护进程,而 “table” 则是指一个表格或者列表,因此 crontab 就是一个用于配置和管理定时任…...
前后端交互系列之Axios详解(包括拦截器)
目录 前言一,服务器的搭建二,Axios的基本使用2.1 Axios的介绍及页面配置2.2 如何安装2.3 Axios的前台代码2.4 Axios的基本使用2.5 axios请求响应结果的结构2.6 带参数的axios请求2.7 axios修改默认配置 三,axios拦截器3.1 什么是拦截器3.2 拦…...
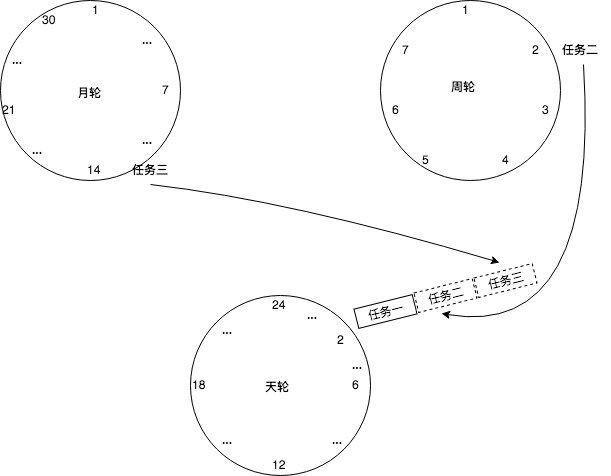
定时任务之时间轮算法
初识时间轮 我们先来考虑一个简单的情况,目前有三个任务A、B、C,分别需要在3点钟,4点钟和9点钟执行,可以把时间想象成一个钟表。 如上图中所示,我只需要把任务放到它需要被执行的时刻,然后等着时针转到这个…...
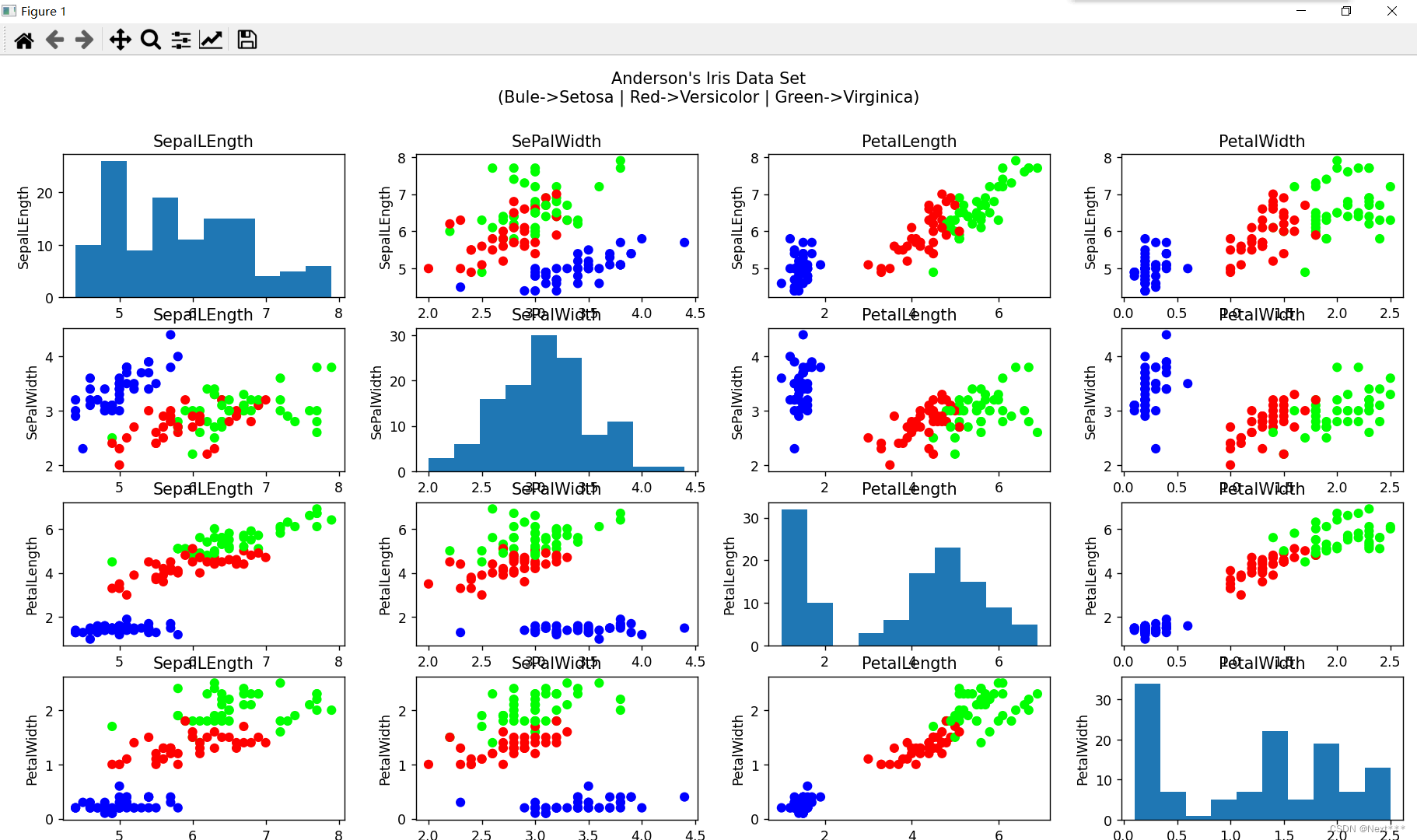
实验4 Matplotlib数据可视化
1. 实验目的 ①掌握Matplotlib绘图基础; ②运用Matplotlib,实现数据集的可视化; ③运用Pandas访问csv数据集。 2. 实验内容 ①绘制散点图、直方图和折线图,对数据进行可视化; ②下载波士顿数房价据集,并…...

【软件工程】为什么要选择软件工程专业?
个人主页:【😊个人主页】 文章目录 前言软件工程💻💻💻就业岗位👨💻👨💻👨💻就业前景🛩️🛩️🛩️工作环…...

5类“计算机”专业很吃香,人才缺口巨大,就业前景良好
说到目前最热门的专业,计算机绝对占有一席之地,是公认的发展前景好、人才缺口大的专业。有人称该专业人数如此众多,势必会导致人才饱和,但是从当前社会互联网发展的趋势来看,计算机专业在很长一段时间都是发展很好的专…...

数仓选型对比
1、数仓选型对比如下(先列举表格,后续逐个介绍) 数仓应用目标产品特点适用于 适用数据类型数据处理速度性能拓展 实施难度运维难度性能优化成本传统数仓(SQLServer、Oracle等关系型数据库)面向主题设计的,为 分析数据而设计基于Oracle、 SQLServer、MyS…...
Java详解与代码实现)
二叉树的遍历(前序、中序、后序)Java详解与代码实现
递归遍历 前序,中序,后序 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val val; }* TreeNode(int val, Tree…...

如何找出消耗CPU最多的线程?
如何找出消耗CPU最多的线程? 1.使用 top -c 找出所有当前进程的运行列表 top -c 2.按P(Shiftp)对所有进程按CPU使用率进行排序,找出消耗最高的线程PID 显示Java进程 PID 为 136 的java进程消耗最 3.使用 top -Hp PID,查出里面消…...

【论文笔记】Attention Augmented Convolutional Networks(ICCV 2019 入选文章)
目录 一、摘要 二、介绍 三、相关工作 卷积网络Convolutional networks: 网络中注意力机制Attention mechanisms in networks: 四、方法 1. 图像的自注意力Self-attention over images: 二维位置嵌入Two-dimensional Positional Enco…...

虚幻图文笔记:Character Creator 4角色通过AutoSetup For Unreal Engine插件导入UE5.1的过程笔记
在UE5端安装AutoSetup For Unreal Engine插件 AutoSetup For Unreal Engine是Reallusion官方提供的免费插件,官方下载地址,下载到的是一个可执行文件,点击安装,记住安装的位置⬇ 看装完毕后会打开一个文件夹,这里就是对…...
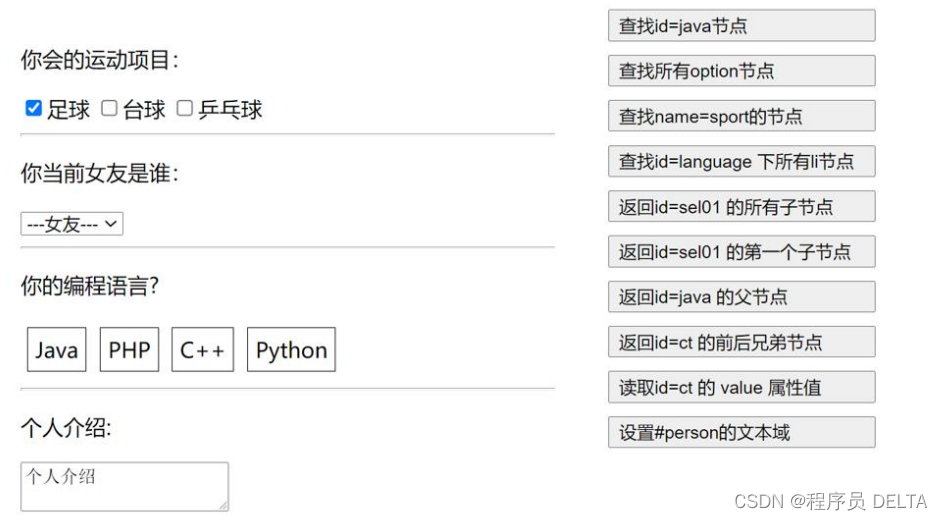
JAVAWeb04-DOM
1. DOM 1.1 概述 1.1.1 官方文档 地址: https://www.w3school.com.cn/js/js_htmldom.asp 1.1.2 DOM 介绍 DOM 全称是 Document Object Model 文档对象模型就是把文档中的标签,属性,文本,转换成为对象来管理 1.2 HTML DOM(文档…...

C++内存管理基础知识
C 内存管理 C内存管理是一个重要的主题,因为它涉及到程序运行时资源的分配和释放。它可以分为三种类型:静态内存、栈内存和堆内存。 静态内存 静态内存(Static Memory):静态内存用于存储全局变量、静态变量和常量。这…...
命令执行漏洞概述
命令执行漏洞概述 命令执行定义命令执行条件命令执行成因命令执行漏洞带来的危害远程命令执行漏洞相关函数assert()preg_replace()call_user_func() a ( a( a(b)可变函数远程命令执行漏洞的利用系统命令执行漏洞相关函数system()exec()shell_exec()passthru(&#x…...

【初试复试第一】脱产在家二战上岸——上交819考研经验
笔者来自通信考研小马哥23上交819全程班学员 先介绍一下自己,我今年初试426并列第一,加上复试之后总分600,电子系第一。 我本科上交,本科期间虽然没有挂科但是成绩排名处于中下游水平。参加过全国电子设计大赛,虽然拿…...
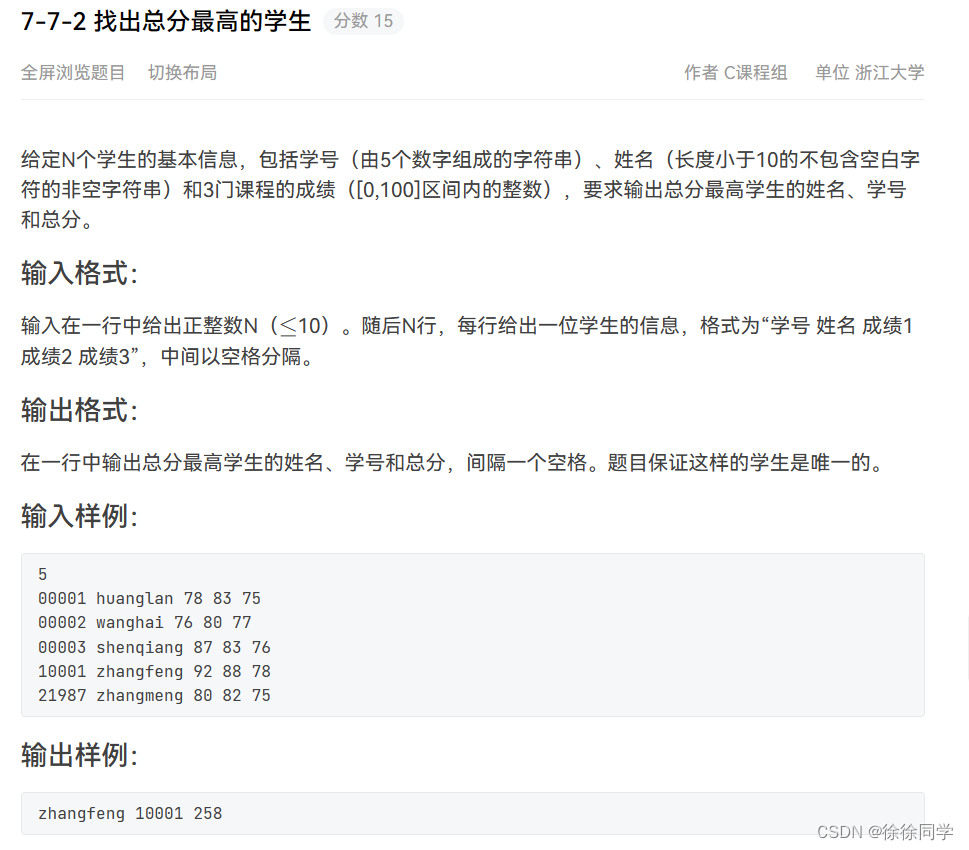
PTA:C课程设计(7)
山东大学(威海)2022级大一下C习题集(7) 函数题7-6-1 递增的整数序列链表的插入7-6-2 查找学生链表7-6-3 统计专业人数7-6-4 建立学生信息链表 编程题7-7-1 查找书籍7-7-2 找出总分最高的学生 函数题 7-6-1 递增的整数序列链表的插…...

POSTGRESQL LINUX 与 PG有关的内存参释义
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
