JsNode算法题acm模式输入
js分为jsNode和JsV8两种输入输出方式,一般的执行代码还是一样的
牛客是两种都支持
华为的题目大多只支持jsNode
本文主要介绍jsNode的输入
JsNode
首先他是逐行输入的,就和py差不多,一定是每行每行地输入,用字符串line(也可以换名字)来接收,用line.split(' ')来分割字符串,从而处理
jsNode最开始的几行代码,都是很麻烦的代码模板,具体作用我不清楚,下面是我尽量简化后的,可以根据自己的情况来改
一、单行单变量输入
比如:123
比如:abc
let cin = require('readline')
const RL = cin.createInterface({input: process.stdin,output: process.stdout
})
RL.on('line', line => {console.log(line) //要是想转化为整数可以(+line)
})
二、单行多变量输入
比如:123 435
比如:abcx asd asd
比如:asd,asd,erer
let cin = require('readline')
const RL = cin.createInterface({input: process.stdin,output: process.stdout
})
let str=""
RL.on('line', line => {str=line.split(' ')let len=str.length;for(let i=0;i<len;i++){console.log(str[i])}
})
三、多行多变量输入
比如:
2
123 234
bca asd
第一行的数2表示下面输入还有2行
let cin = require('readline')
const RL = cin.createInterface({input: process.stdin,output: process.stdout
})
let T = 1 //进入RL函数的次数
let str=""
RL.on('line', line => {str=line.split(' ')if(T==1){ //第一次进的时候,str[0]就是接下来输入的行数n=+str[0] mp=new Array(n) //开一个大小为n的数组}else{mp[T-2]=str //接下来每输入一行,T会+1,根据T来判断输入是第几行的数据if(T==n+1){ //要是T=n+1了(自己计算出的),表示是最后一行输入//这时要进行算法代码运行,因为全部数据输入完了for(let i=0;i<n;i++)console.log(mp[i])}}T++
})
通过代码可以看出,sjNode的输入,RL函数要不断进入,每次进入时line就是一行的输入
所以要用T这种全局变量来记录进入的次数,通过判断T,来存储数据
这个输入模板也算是最全的,即是是单行也建议用这个。
相关文章:

JsNode算法题acm模式输入
js分为jsNode和JsV8两种输入输出方式,一般的执行代码还是一样的 牛客是两种都支持 华为的题目大多只支持jsNode 本文主要介绍jsNode的输入 JsNode 首先他是逐行输入的,就和py差不多,一定是每行每行地输入,用字符串line&#x…...

Javaweb小练习---在JSP中使用Javabean访问数据库完成用户信息的简单添加
Javaweb小练习---在JSP中使用Javabean访问数据库完成用户信息的简单添加 目录 Javaweb小练习---在JSP中使用Javabean访问数据库完成用户信息的简单添加 0.创建数据库 1. 在resources目录下创建db.properties文件 2. /** * 获取链接与释放资源的工具类--JdbcUtil类 */ 3…...

(十七)排序算法-基数排序
1 基本介绍 1.1 概述 (1)基数排序(radix sort)属于“分配式排序”,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用。 (2&#x…...
详解)
JMM之先行发生原则(happens-before)详解
1、概述 在JMM规范下,如果一个操作执行的结果需要对另一个操作可见,那么这两个操作之间必须存在happers-before(先行发生)原则。 例如 int x 10 ; int y x; 这两行代码中第二个操作 yx ,因为需要将x值赋值给y,所以第一行代码的…...

含分布式电源的配电网可靠性评估研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

安全加固服务是什么?哪些行业需要做?
安全加固服务是什么?安全加固服务是一种针对企业信息系统、网络设备、应用程序等进行安全加固和优化的服务。安全加固服务的主要目的是保障企业信息系统的安全性和稳定性,有效防范各类网络攻击和安全威胁。 安全加固服务是什么?通常包括以下…...

好程序员:Java书籍推荐,程序员必看的5本Java书籍,赶紧收藏!
今天好程序员给大家推荐5本Java书籍,各大高校都在使用(具体名单如下),所有学习Java的程序员都不应该错过! 第一本Java书籍《Java EE(SSM框架)企业应用实战》 本书全面介绍了JavaEE中MyBatis、Sp…...
maven将jar包添加到本地仓库
第一步:下载需要添加的jar包 可以在maven库中查找下载,也可以在对应官网下载 maven库网址:https://mvnrepository.com/ 找到对应版本的jar包下载 第二步:将下载的jar包放到指定位置(位置自己指定)…...
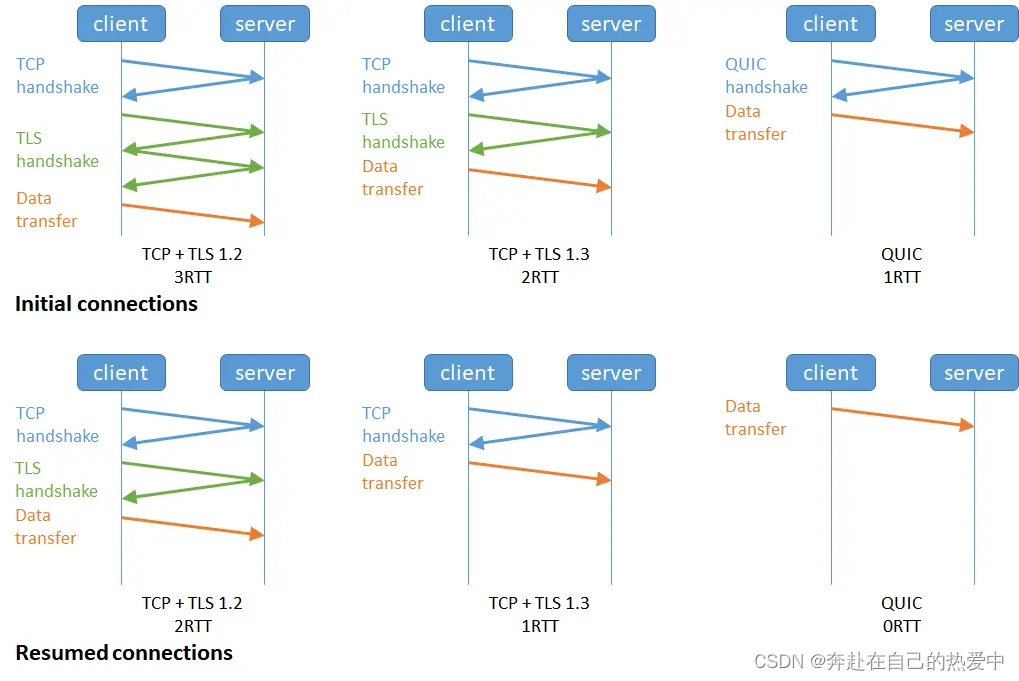
4.12--计算机网络之TCP篇之TCP 协议的缺陷+如何基于 UDP 协议实现可靠传输?--(复习+大总结)---沉下心来(加油呀)
TCP 协议四个方面的缺陷: 1.升级 TCP 的工作很困难; TCP 协议是在内核中实现的,应用程序只能使用不能修改,如果要想升级 TCP 协议,那么只能升级内核。 而升级内核这个工作是很麻烦的事情 2.TCP 建立连接的延迟&#x…...

数据库网络编程
数据库网络编程是一个重要的领域,它涉及到如何使用编程语言与数据库进行交互,以及如何设计和实现网络应用程序。在这篇文章中,我将探讨数据库网络编程的基础知识、常用技术和实践经验,以及一些应用案例和未来发展趋势。 一、基础…...

为什么现代企业都在使用ERP系统 它有哪些优势
随着科技的不断发展,企业管理方式也在不断地发生改变。在这个信息化的时代,企业要想取得成功,必须要善于利用先进的信息化技术工具。其中,ERP系统是企业管理中不可或缺的重要工具。本文将探讨现代企业为什么会使用ERP系统…...

别再用 BeanUtils 了,这款 PO VO DTO 转换神器不香么?
老铁们是不是经常为写一些实体转换的原始代码感到头疼,尤其是实体字段特别多的时候。介绍一个开源项目 mapstruct ,可以轻松优雅的进行转换,简化你的代码。当然有的人喜欢写get set,或者用BeanUtils 进行复制,代码只是…...
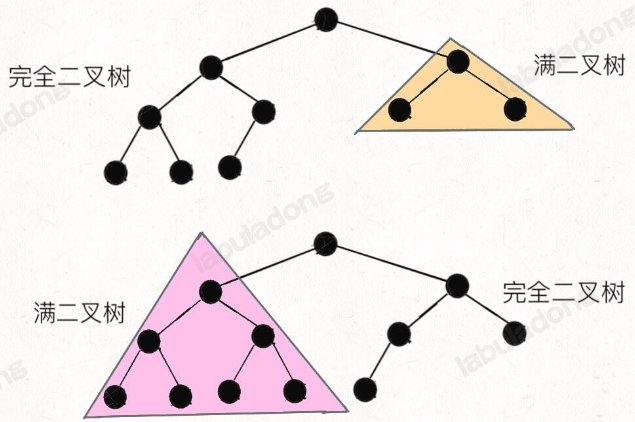
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数 最近公共祖先[236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)[235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-b…...
)
php、redis实现分布式锁的正确写法(原子操作 通用类 加讲解)
最终代码(通用类) 1 面试中、实际工作中,经常涉及到 redis 分布式锁,正确写法如下。先奉上代码,再讲解。 <?php namespace app\common\library; /*** 通用分布式锁(原子操作)*/ class Lock {/*** 获取redis实例* return \Redis* throws…...
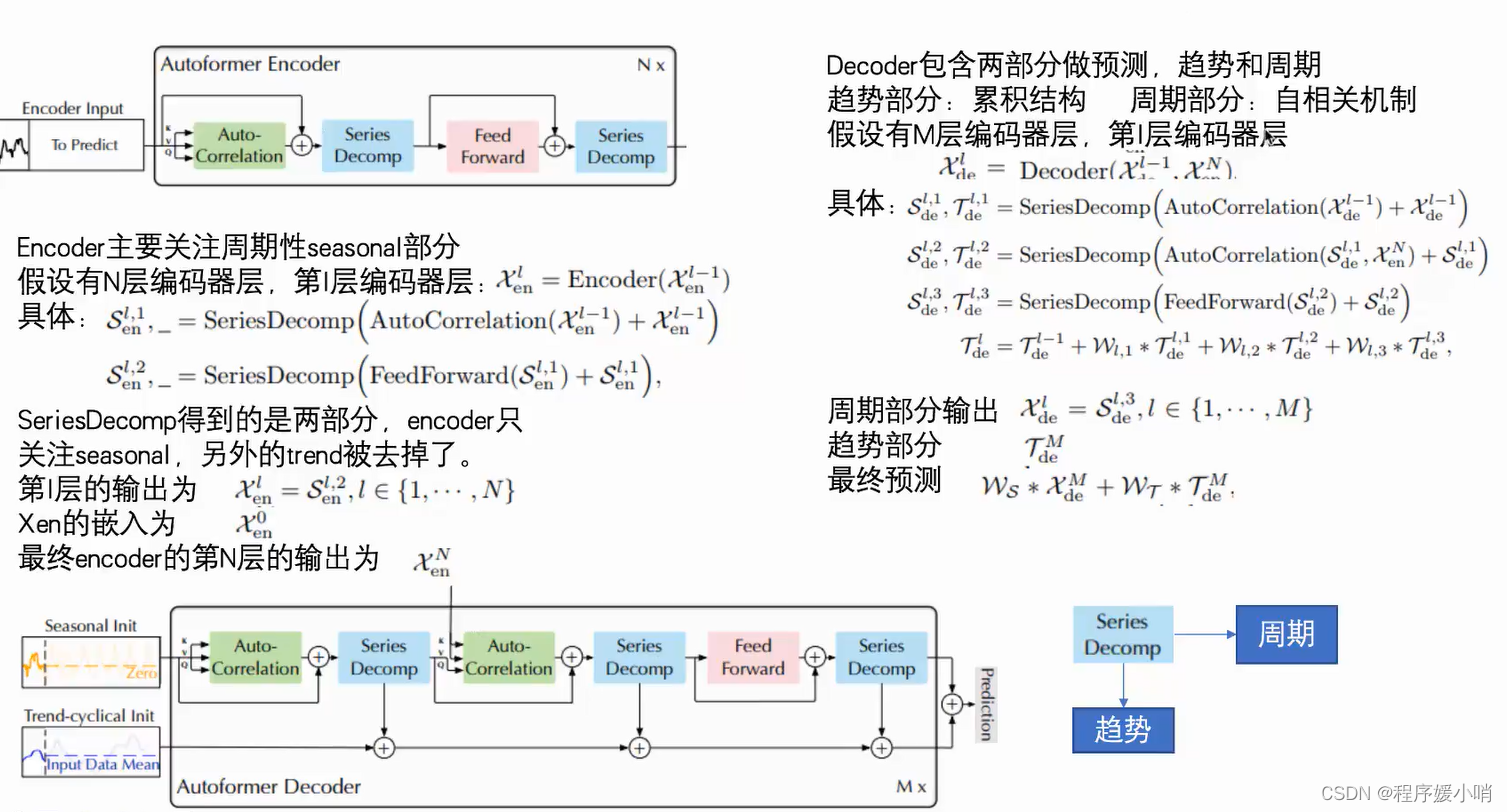
Transformer在时序预测的应⽤第一弹——Autoformer
Transformer在时序预测的应⽤第一弹——Autoformer 原文地址:Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting(NIPS 2021) 做长时间序列的预测 Decomposition把时间序列做拆分,…...
文章改写神器在线-AI续写文章生成器
AI续写生成器 AI续写生成器是一种利用人工智能技术的创意工具,能够提高写作效率,为营销推广带来全新的可能性。无论你是写手、广告人员还是市场营销人员,这个工具都能够有效地解决你在写作中遇到的难题。 在内容创作行业中,原创…...
一秒钟给硬盘文件做个树状结构目录
一秒钟给硬盘文件做个树状结构目录 一、背景 对于长时间坐在电脑前的打工人来说,若没有养成良好文件分类习惯的话,年终整理电脑文件绝对是件头疼的事情。 给磁盘文件做个目录,一目了然文件都在哪里?想想都是件头疼的事情。 对于…...
电脑重装系统后会怎样?
有小伙伴的电脑系统运行缓慢卡顿,现在想通过重装系统来解决问题。咨询电脑重装系统会怎么样对系统有影响吗,现在小编就带大家看看电脑重装系统后会怎样。 方法/步骤: 一、电脑重装系统会怎么样 1、我们的电脑重装系统后,电脑…...

100种思维模型之反熵增思维模型-47
查理芒格被誉为反熵增思维模型的倡导者。本文将介绍查理芒格的反熵增思维模型,并分析它的实用性。 一、什么是熵增? 在物理学中,熵是衡量系统无序程度的指标。系统的熵越高,其无序程度越高。这个概念也可以应用到其他领域。在金融…...
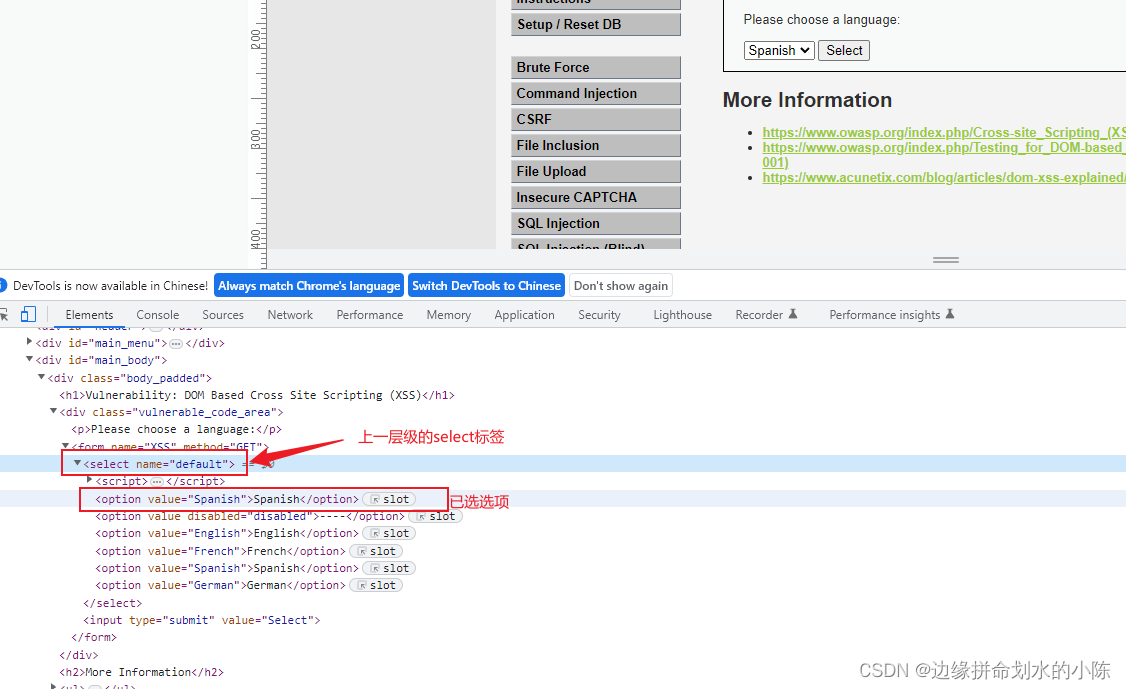
【网络安全】Xss漏洞
xss漏洞 xss漏洞介绍危害防御方法xss测试语句xss攻击语句1. 反射性xss2.存储型xss3.DOM型xssdvwa靶场各等级渗透方法xss反射型(存储型方法一致)LowMediumHightimpossible Dom型LowMediumHight xss漏洞介绍 定义:XSS 攻击全称跨站脚本攻击&am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
