LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数
- 最近公共祖先
- [236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
- [235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)
- [剑指 Offer 68 - I. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/)
- 完全二叉树的节点个数
- [222. 完全二叉树的节点个数](https://leetcode.cn/problems/count-complete-tree-nodes/)
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计4935字,阅读大概需要3分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
最近公共祖先
Git 是如何找到两条不同分支的最近公共祖先(Lowest Common Ancestor,简称 LCA)的呢?这是一个经典的算法问题
Git 是如何合并两条分支并检测冲突的呢?
以 rebase 命令为例,比如下图的情况,我站在 dev 分支执行 git rebase master,然后 dev 就会接到 master 分支之上:

这个过程中,Git 是这么做的:
首先,找到这两条分支的最近公共祖先LCA,然后从master节点开始,重演LCA到dev的commit的修改,如果这些修改和LCA到master的commit有冲突,就会提示你手动解决冲突,最后的结果就是把dev的分支完全接到master上面。
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
如果一个节点能够在它的左右子树中分别找到p和q,则该节点为LCA节点
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {return find(root, p.val, q.val);}// 在二叉树中寻找 val1 和 val2 的最近公共祖先节点 private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;// 前序位置if(root.val == val1 || root.val == val2){// 如果遇到目标值,直接返回return root;}TreeNode left = find(root.left, val1, val2);TreeNode right = find(root.right, val1, val2);// 后序位置,已经知道左右子树是否存在目标值if(left != null && right != null){return root;}return left != null ? left : right;}
}
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Mwos0c4s-1681899253749)(E:/typora/binarysearchtree_improved.png)]
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
但对于 BST 来说,根本不需要老老实实去遍历子树,由于 BST 左小右大的性质,将当前节点的值与val1和val2作对比即可判断当前节点是不是LCA:
假设val1 < val2,那么val1 <= root.val <= val2则说明当前节点就是LCA;若root.val比val1还小,则需要去值更大的右子树寻找LCA;若root.val比val2还大,则需要去值更小的左子树寻找LCA。
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 保证 val1 较小,val2 较大int val1 = Math.min(p.val, q.val);int val2 = Math.max(p.val, q.val);return find(root, val1, val2);}// 在 BST 中寻找 val1 和 val2 的最近公共祖先节点private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;if(root.val > val2){// 当前节点太大,去左子树找return find(root.left, val1, val2);}if(root.val < val1){// 当前节点太小,去右子树找return find(root.right, val1, val2);}// val1 <= root.val <= val2// 则当前节点就是最近公共祖先return root;}
}
这道题目跟👆一样
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5OrUzHc7-1681899253750)(E:/typora/binarysearchtree_improved.png)]
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 保证 val1 较小,val2 较大int val1 = Math.min(p.val, q.val);int val2 = Math.max(p.val, q.val);return find(root, val1, val2);}// 在 BST 中寻找 val1 和 val2 的最近公共祖先节点private TreeNode find(TreeNode root, int val1, int val2){if(root == null) return null;if(root.val > val2){// 当前节点太大,去左子树找return find(root.left, val1, val2);}if(root.val < val1){// 当前节点太小,去右子树找return find(root.right, val1, val2);}// val1 <= root.val <= val2// 则当前节点就是最近公共祖先return root;}
}
完全二叉树的节点个数
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
完全二叉树如下图,每一层都是紧凑靠左排列的:

满二叉树如下图,是一种特殊的完全二叉树,每层都是是满的,像一个稳定的三角形

一棵完全二叉树的两棵子树,至少有一棵是满二叉树:
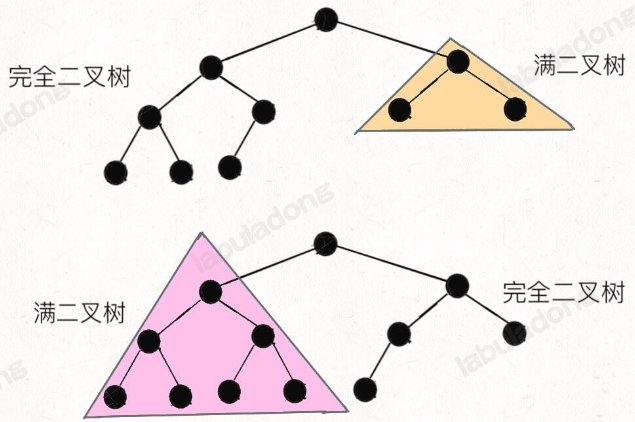
如何求一棵完全二叉树的节点个数呢?
如果是一个普通二叉树,显然只要向下面这样遍历一边即可,时间复杂度 O(N)
public int countNodes(TreeNode root) {if (root == null) return 0;return 1 + countNodes(root.left) + countNodes(root.right);
}
那如果是一棵满二叉树,节点总数就和树的高度呈指数关系
public int countNodes(TreeNode root) {int h = 0;// 计算树的高度while (root != null) {root = root.left;h++;}// 节点总数就是 2^h - 1return (int)Math.pow(2, h) - 1;
}
完全二叉树比普通二叉树特殊,但又没有满二叉树那么特殊,计算它的节点总数,可以说是普通二叉树和完全二叉树的结合版
public int countNodes(TreeNode root) {TreeNode l = root, r = root;// 沿最左侧和最右侧分别计算高度int hl = 0, hr = 0;while (l != null) {l = l.left;hl++;}while (r != null) {r = r.right;hr++;}// 如果左右侧计算的高度相同,则是一棵满二叉树if (hl == hr) {return (int)Math.pow(2, hl) - 1;}// 如果左右侧的高度不同,则按照普通二叉树的逻辑计算return 1 + countNodes(root.left) + countNodes(root.right);
}
算法的递归深度就是树的高度 O(logN),每次递归所花费的时间就是 while 循环,需要 O(logN),所以总体的时间复杂度是 O(logN*logN)
–end–
相关文章:

LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数 最近公共祖先[236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)[235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-b…...
)
php、redis实现分布式锁的正确写法(原子操作 通用类 加讲解)
最终代码(通用类) 1 面试中、实际工作中,经常涉及到 redis 分布式锁,正确写法如下。先奉上代码,再讲解。 <?php namespace app\common\library; /*** 通用分布式锁(原子操作)*/ class Lock {/*** 获取redis实例* return \Redis* throws…...
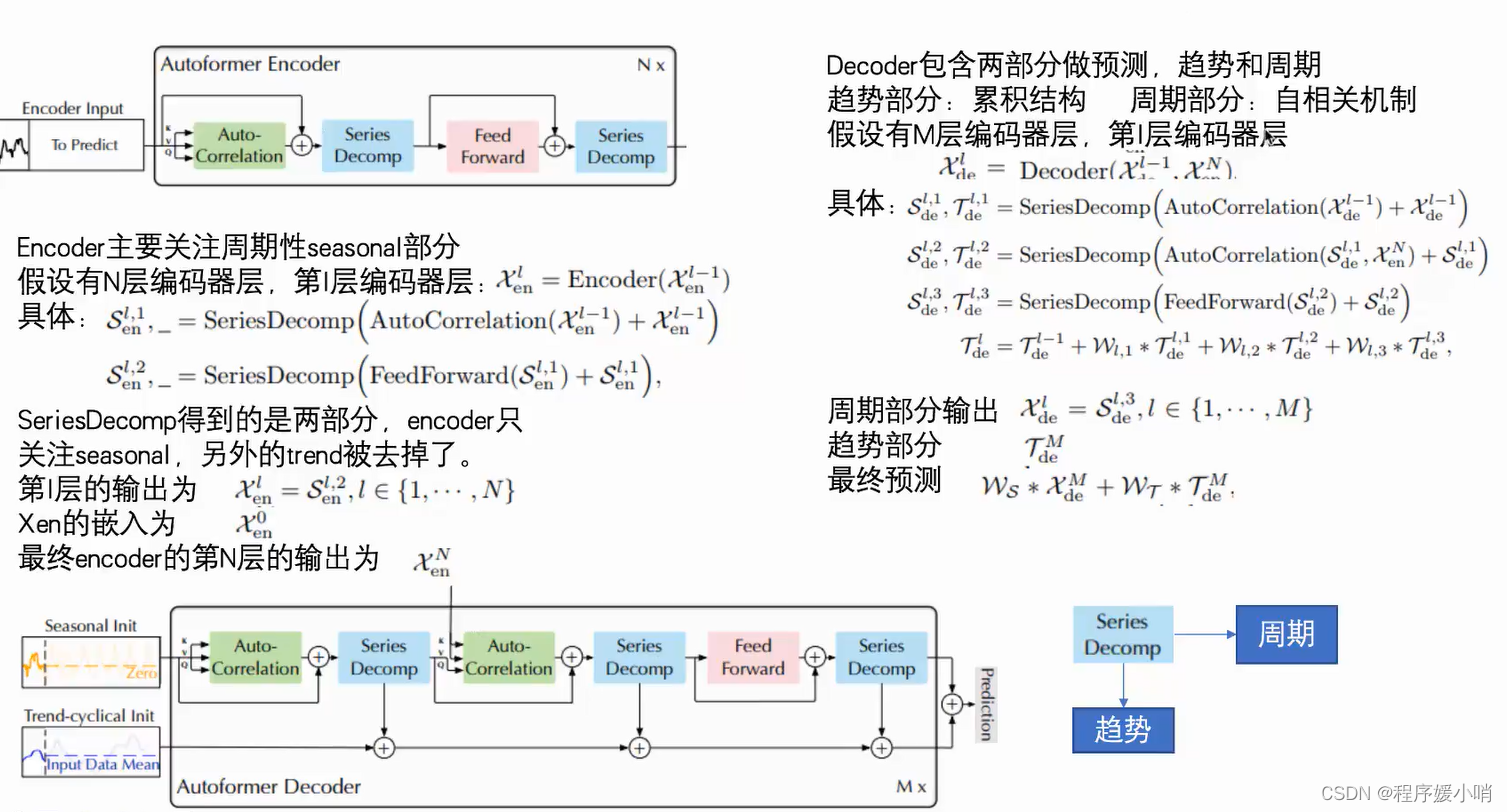
Transformer在时序预测的应⽤第一弹——Autoformer
Transformer在时序预测的应⽤第一弹——Autoformer 原文地址:Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting(NIPS 2021) 做长时间序列的预测 Decomposition把时间序列做拆分,…...
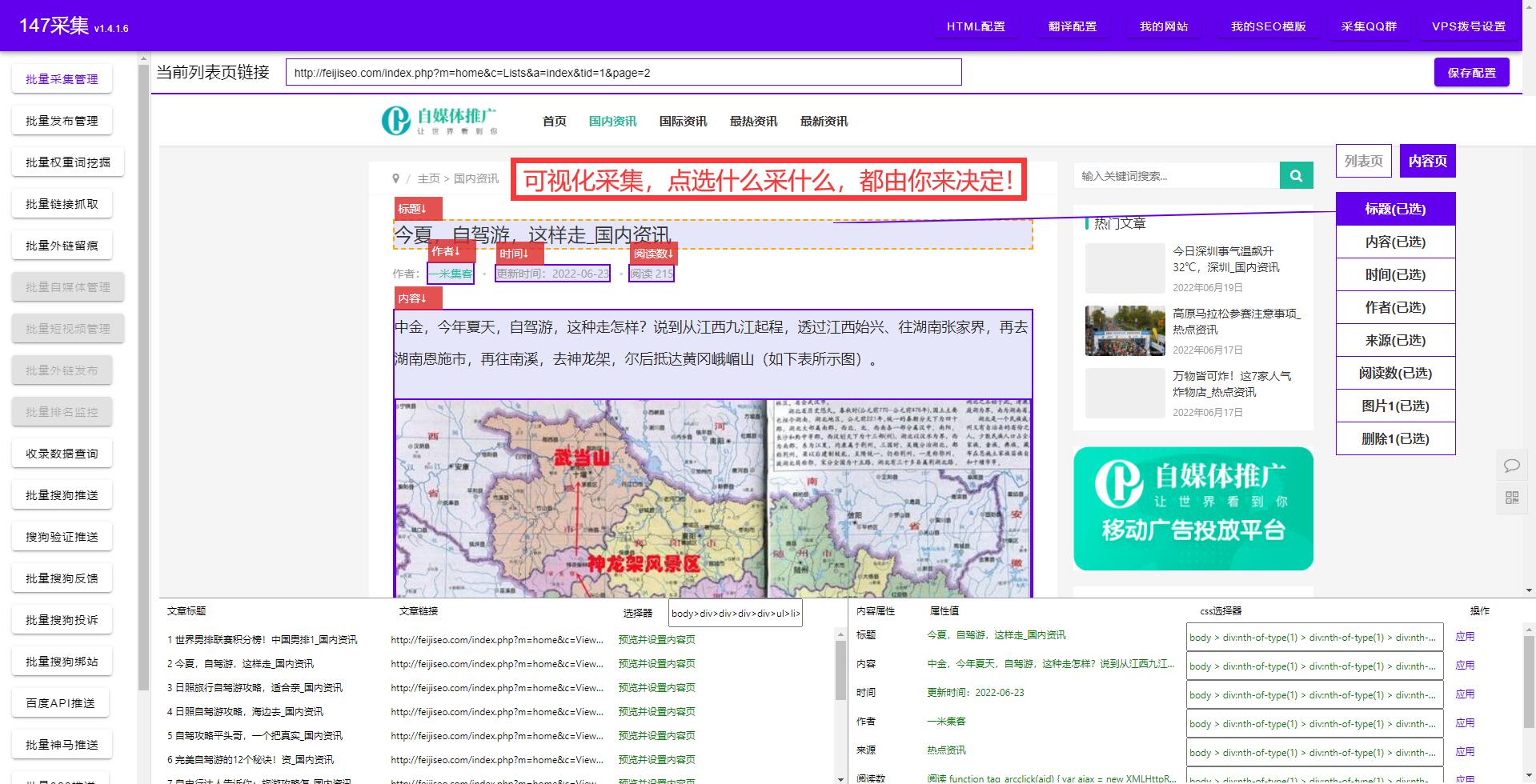
文章改写神器在线-AI续写文章生成器
AI续写生成器 AI续写生成器是一种利用人工智能技术的创意工具,能够提高写作效率,为营销推广带来全新的可能性。无论你是写手、广告人员还是市场营销人员,这个工具都能够有效地解决你在写作中遇到的难题。 在内容创作行业中,原创…...
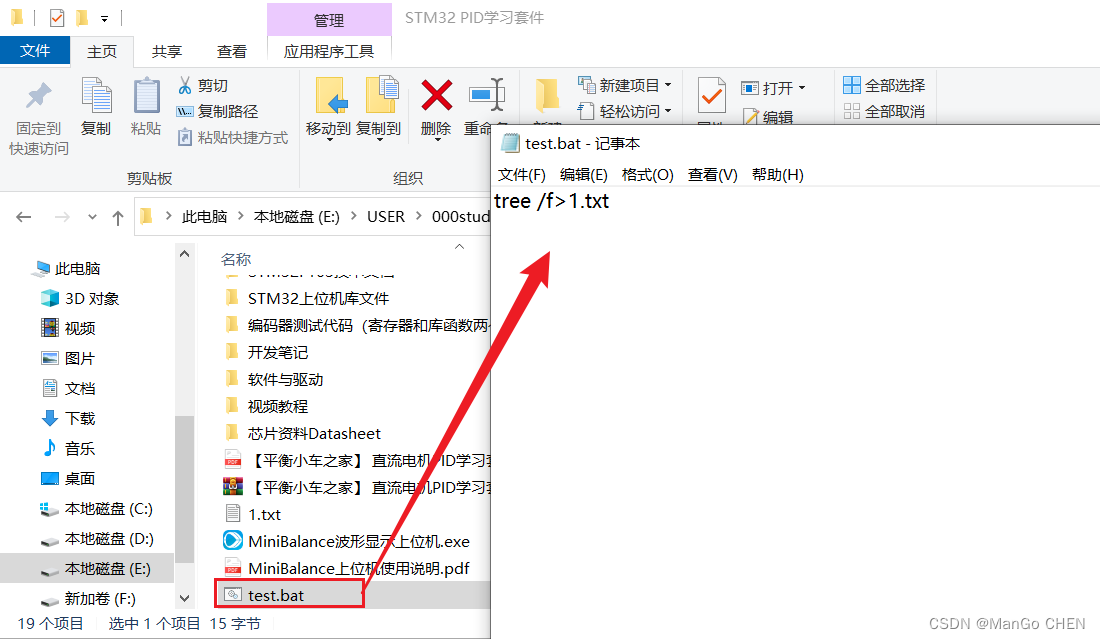
一秒钟给硬盘文件做个树状结构目录
一秒钟给硬盘文件做个树状结构目录 一、背景 对于长时间坐在电脑前的打工人来说,若没有养成良好文件分类习惯的话,年终整理电脑文件绝对是件头疼的事情。 给磁盘文件做个目录,一目了然文件都在哪里?想想都是件头疼的事情。 对于…...
电脑重装系统后会怎样?
有小伙伴的电脑系统运行缓慢卡顿,现在想通过重装系统来解决问题。咨询电脑重装系统会怎么样对系统有影响吗,现在小编就带大家看看电脑重装系统后会怎样。 方法/步骤: 一、电脑重装系统会怎么样 1、我们的电脑重装系统后,电脑…...

100种思维模型之反熵增思维模型-47
查理芒格被誉为反熵增思维模型的倡导者。本文将介绍查理芒格的反熵增思维模型,并分析它的实用性。 一、什么是熵增? 在物理学中,熵是衡量系统无序程度的指标。系统的熵越高,其无序程度越高。这个概念也可以应用到其他领域。在金融…...
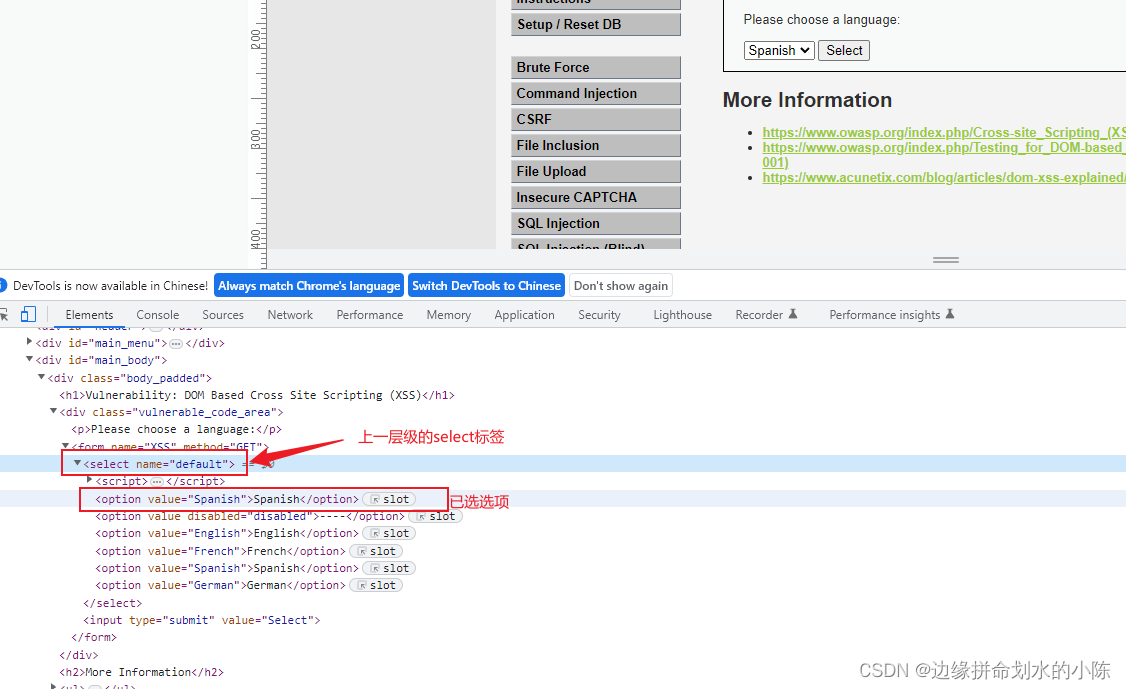
【网络安全】Xss漏洞
xss漏洞 xss漏洞介绍危害防御方法xss测试语句xss攻击语句1. 反射性xss2.存储型xss3.DOM型xssdvwa靶场各等级渗透方法xss反射型(存储型方法一致)LowMediumHightimpossible Dom型LowMediumHight xss漏洞介绍 定义:XSS 攻击全称跨站脚本攻击&am…...
17.网络爬虫—Scrapy入门与实战
这里写目录标题 Scrapy基础Scrapy运行流程原理Scrapy的工作流程Scrapy的优点 Scrapy基本使用(豆瓣网为例)创建项目创建爬虫配置爬虫运行爬虫如何用python执行cmd命令数据解析打包数据打开管道pipeline使用注意点 后记 前言: 🏘️🏘️个人简介…...

【面试题】JavaScript 中 try...catch 的使用技巧 ?
大厂面试题分享 面试题库 前后端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 web前端面试题库 VS java后端面试题库大全 作为一位 Web 前端工程师,JavaScript 中的 try...catch 是我们常用的特性之一。…...

Java 命名格式规范
Java 命名格式规范 概述 简洁清爽的代码风格应该是大多数开发工程师所期待的。在编码过程中笔者常常因为起名字而纠结,夸张点可以说是编程 5 分钟,命名两小时!究竟为什么命名成为了编码中的拦路虎。 每个公司都有不同的标准,目…...

【C++】STL中的容器适配器 stack queue 和 priority_queue 的模拟实现
STL中的容器适配器 一、容器适配器1、什么是容器适配器2、STL标准库中的容器适配器 二、stack的模拟实现1、stack的简单介绍2、栈的模拟实现 三、queue的模拟实现1、queue的简单介绍2、queue的模拟实现 四、priority_queue的模拟实现1、priority_queue的简单介绍2、priority_qu…...

MongoDB 聚合管道中使用算术表达式运算符
算术表达式运算符主要用于实现数字之间的算术运算,主要包含了对加、减、乘、除、余数、截取、舍入等算术操作。 下面我们进行详细介绍: 一、准备数据 初始化商品数据 db.goods.insertMany([{ "_id": 1, name: "薯片", size: &q…...

代码随想录算法训练营第四十三天-动态规划5|1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,…...

《淘宝网店》:计算总收益
目录 一、题目 二、思路 1、当两个年份不一样的时候 (1)from年剩余之后的收益 (2)中间年份的全部收益 (3)to年有的收益 2、同一个年份 三、代码 详细注释版本: 简化注释版本ÿ…...

2023年03月青少年软件编程C语言一级真题答案——持续更新.....
1.字符长方形 给定一个字符,用它构造一个长为4个字符,宽为3个字符的长方形,可以参考样例输出。 时间限制:1000 内存限制:65536 输入 输入只有一行, 包含一个字符。 输出 该字符构成的长方形,长4个字符,宽3个字符。 样例输入 * 样例输出 **** **** ****#include<bi…...

家用洗地机好用吗?好用的洗地机分享
洗地机是一种高效、节能、环保的清洁设备,广泛应用于各种场所的地面清洁工作。它不仅可以快速清洁地面,还可以有效去除污渍、油渍等难以清洁的污染物,让地面恢复光洁如新的状态。同时,洗地机还可以减少清洁人员的劳动强度…...
《分解因数》:质因数分解
目录 一、题目: 二、思路: 三、代码: 一、题目: 分解因数 《分解因数》题目链接 所谓因子分解,就是把给定的正整数a,分解成若干个素数的乘积,即 a a1 a2 a3 ... an,并且 1 < a1…...
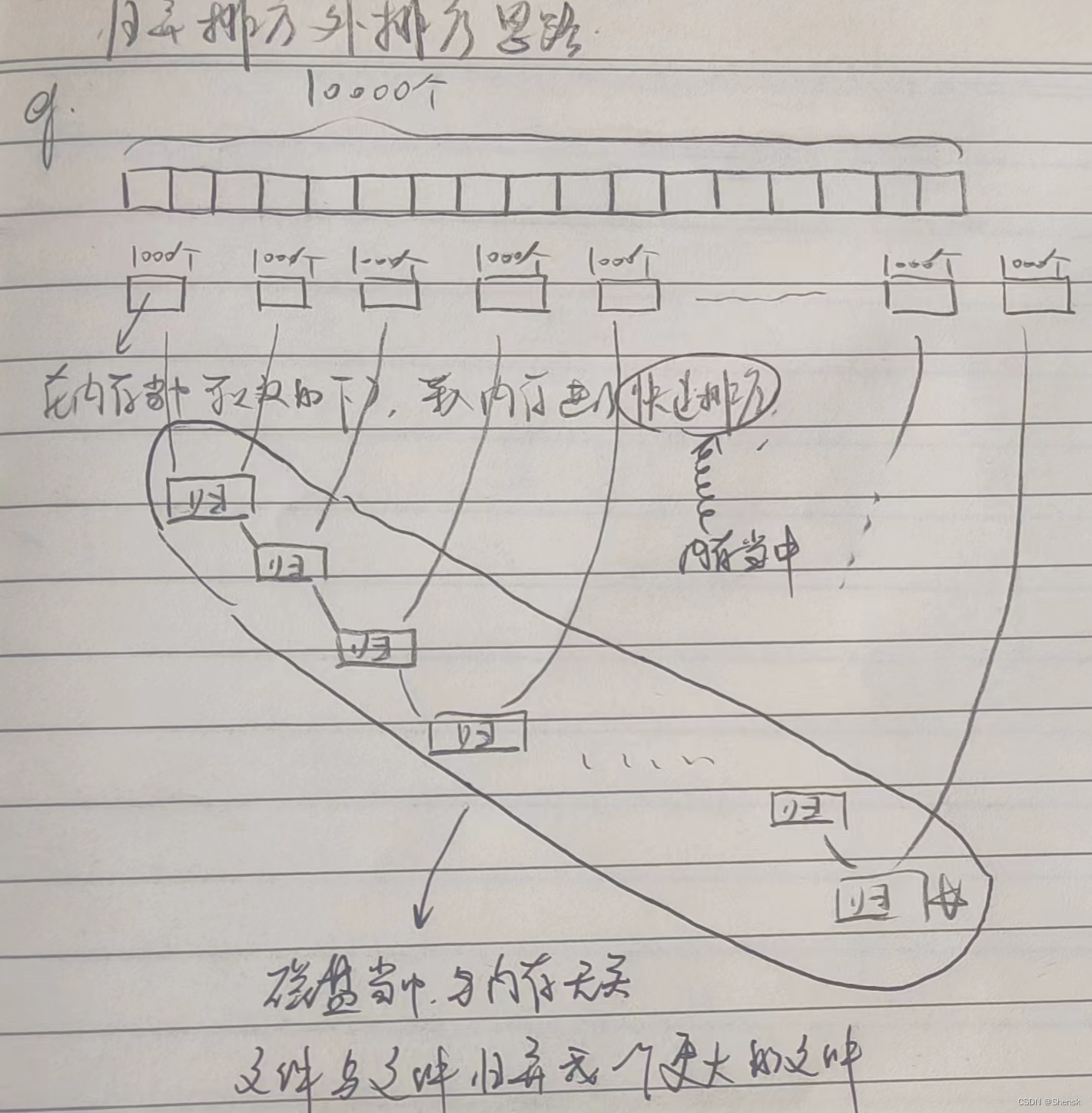
(排序10)归并排序的外排序应用(文件排序)
TIPS 在一些文件操作函数当中,fputc与fgetc这两个函数都是针对字符的,如果说你需要往文件里面去放入整形啊等等,不是字符的类型,这时候就用fprintf,fscanf在参数里面数据类型控制一下就可以。但是话说回来,…...
浅谈根号分治与分块
文章目录 1. 根号分治哈希冲突 2. 线性分块引入教主的魔法[CQOI2011] 动态逆序对[国家集训队] 排队[HNOI2010] 弹飞绵羊蒲公英 1. 根号分治 哈希冲突 题目1 n n n 个数, m m m 次操作。操作 1 为修改某一个数的值,操作 2 为查询所有满足下标模 x x x …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
