100种思维模型之反熵增思维模型-47
查理芒格被誉为反熵增思维模型的倡导者。本文将介绍查理芒格的反熵增思维模型,并分析它的实用性。
一、什么是熵增?
在物理学中,熵是衡量系统无序程度的指标。系统的熵越高,其无序程度越高。这个概念也可以应用到其他领域。在金融投资中,熵增可以理解为市场中信息的无序性增加,使得投资者难以找到有价值的信息。
二、什么是反熵增思维模型?
反熵增思维模型是一种通过积极寻找、筛选和利用有价值的信息,以最小的代价获得最大的收益的思维方式。这种思维方式与传统的随波逐流、被动跟从的思维方式相反。反熵增思维模型强调在市场中寻找那些被其他投资者忽视或低估的信息,通过更好地理解市场和企业的基本面,实现长期稳健的投资回报。
三、如何实践反熵增思维模型?
-
系统化思考 反熵增思维模型的核心是系统化思考。在分析一个问题时,要将它拆分成几个可管理的部分,以便更好地理解和解决它。这种系统化思考可以采用树状图、思维导图等工具来辅助。通过将问题分解成各个部分并逐一分析,可以更好地理解整个问题,更快地找到解决方案。
-
专注于重要细节 Munger提倡专注于重要细节。这意味着要有能力辨别哪些是最重要的因素,哪些是次要的或无关紧要的。只有掌握了最重要的细节,才能做出明智的决策。因此,在面对问题时,要着眼于问题的核心,避免被琐碎的细节所迷惑。
-
跨学科学习 Munger认为,要成为一名成功的投资者,需要具备广泛的知识和跨学科的能力。因此,建议花时间学习与自己领域相关的其他领域,掌握不同学科的知识,这有助于提高自己的综合素质,更好地理解问题和做出决策。
-
不断反思和总结 反熵增思维模型要求人们不断反思和总结。在解决问题后,要总结经验,找出问题和错误,以避免再次犯错。反思和总结是不断进步的关键,也是不断学习和提高的重要手段。
四、反熵增思维模型在投资领域应用
在股票投资中,反熵增思维模型可以帮助投资者更好地分析公司的竞争力和长期价值,从而做出明智的投资决策。下面以伯克希尔·哈撒韦公司(Berkshire Hathaway)在收购可口可乐公司(Coca-Cola)时的案例来说明。
可口可乐是世界上最知名的品牌之一,也是世界上最大的非酒精饮料公司之一。在20世纪80年代末,可口可乐公司的股票价格相对较低,吸引了伯克希尔·哈撒韦公司的注意。查理·芒格和沃伦·巴菲特是伯克希尔·哈撒韦公司的两位著名投资者,他们采用反熵增思维模型来分析可口可乐公司的长期价值和竞争力。
首先,他们使用系统化思考,将可口可乐公司拆分成多个部分,并逐一分析。他们发现,可口可乐公司在全球范围内有着强大的品牌影响力,可以在各个国家和地区的市场上占据领先地位。同时,可口可乐公司拥有先进的生产工艺和广泛的销售渠道,能够保持其在饮料市场的竞争力。
其次,他们专注于重要细节。他们发现,可口可乐公司的主要收入来自于碳酸饮料,而可口可乐是这个市场的领导者。此外,他们发现可口可乐公司的市值相对较低,而公司的股票价格已经稳定了几年,说明可口可乐公司的财务稳健。这些因素都显示出可口可乐公司长期价值的潜力。
最后,他们不断反思和总结。伯克希尔·哈撒韦公司最终决定收购可口可乐公司,成为其最大的股东之一。事实证明,这项投资是成功的,可口可乐公司的股票价格逐渐上涨,公司的市值也随之增加。
这个案例说明了反熵增思维模型在投资领域的应用。通过系统化思考、专注于重要细节和不断反思总结,芒格和巴菲特成功地分析了可口可乐公司的竞争力和长期价值,
总之,反熵增思维模型可以帮助人们更好地处理复杂问题,理清思路,找出关键因素,做出更明智的决策。实践这种思维模型需要不断努力和训练,但只要坚持下去,就能在自己的领域内取得成功。
相关文章:

100种思维模型之反熵增思维模型-47
查理芒格被誉为反熵增思维模型的倡导者。本文将介绍查理芒格的反熵增思维模型,并分析它的实用性。 一、什么是熵增? 在物理学中,熵是衡量系统无序程度的指标。系统的熵越高,其无序程度越高。这个概念也可以应用到其他领域。在金融…...
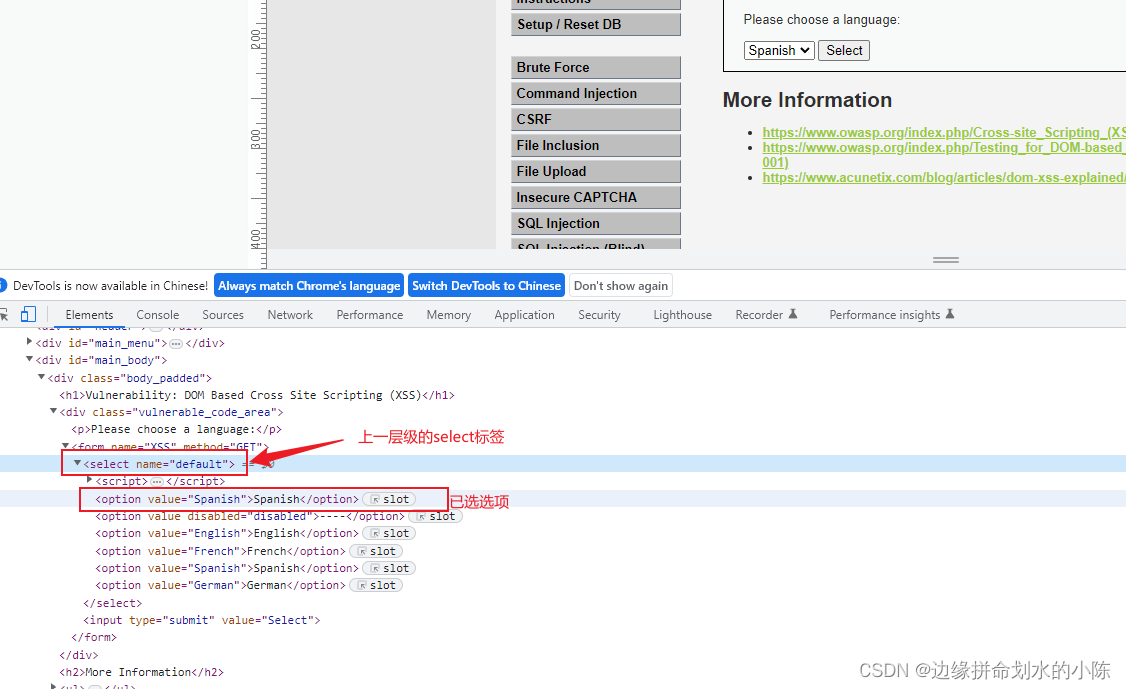
【网络安全】Xss漏洞
xss漏洞 xss漏洞介绍危害防御方法xss测试语句xss攻击语句1. 反射性xss2.存储型xss3.DOM型xssdvwa靶场各等级渗透方法xss反射型(存储型方法一致)LowMediumHightimpossible Dom型LowMediumHight xss漏洞介绍 定义:XSS 攻击全称跨站脚本攻击&am…...
17.网络爬虫—Scrapy入门与实战
这里写目录标题 Scrapy基础Scrapy运行流程原理Scrapy的工作流程Scrapy的优点 Scrapy基本使用(豆瓣网为例)创建项目创建爬虫配置爬虫运行爬虫如何用python执行cmd命令数据解析打包数据打开管道pipeline使用注意点 后记 前言: 🏘️🏘️个人简介…...

【面试题】JavaScript 中 try...catch 的使用技巧 ?
大厂面试题分享 面试题库 前后端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 web前端面试题库 VS java后端面试题库大全 作为一位 Web 前端工程师,JavaScript 中的 try...catch 是我们常用的特性之一。…...

Java 命名格式规范
Java 命名格式规范 概述 简洁清爽的代码风格应该是大多数开发工程师所期待的。在编码过程中笔者常常因为起名字而纠结,夸张点可以说是编程 5 分钟,命名两小时!究竟为什么命名成为了编码中的拦路虎。 每个公司都有不同的标准,目…...

【C++】STL中的容器适配器 stack queue 和 priority_queue 的模拟实现
STL中的容器适配器 一、容器适配器1、什么是容器适配器2、STL标准库中的容器适配器 二、stack的模拟实现1、stack的简单介绍2、栈的模拟实现 三、queue的模拟实现1、queue的简单介绍2、queue的模拟实现 四、priority_queue的模拟实现1、priority_queue的简单介绍2、priority_qu…...

MongoDB 聚合管道中使用算术表达式运算符
算术表达式运算符主要用于实现数字之间的算术运算,主要包含了对加、减、乘、除、余数、截取、舍入等算术操作。 下面我们进行详细介绍: 一、准备数据 初始化商品数据 db.goods.insertMany([{ "_id": 1, name: "薯片", size: &q…...

代码随想录算法训练营第四十三天-动态规划5|1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,…...

《淘宝网店》:计算总收益
目录 一、题目 二、思路 1、当两个年份不一样的时候 (1)from年剩余之后的收益 (2)中间年份的全部收益 (3)to年有的收益 2、同一个年份 三、代码 详细注释版本: 简化注释版本ÿ…...

2023年03月青少年软件编程C语言一级真题答案——持续更新.....
1.字符长方形 给定一个字符,用它构造一个长为4个字符,宽为3个字符的长方形,可以参考样例输出。 时间限制:1000 内存限制:65536 输入 输入只有一行, 包含一个字符。 输出 该字符构成的长方形,长4个字符,宽3个字符。 样例输入 * 样例输出 **** **** ****#include<bi…...

家用洗地机好用吗?好用的洗地机分享
洗地机是一种高效、节能、环保的清洁设备,广泛应用于各种场所的地面清洁工作。它不仅可以快速清洁地面,还可以有效去除污渍、油渍等难以清洁的污染物,让地面恢复光洁如新的状态。同时,洗地机还可以减少清洁人员的劳动强度…...
《分解因数》:质因数分解
目录 一、题目: 二、思路: 三、代码: 一、题目: 分解因数 《分解因数》题目链接 所谓因子分解,就是把给定的正整数a,分解成若干个素数的乘积,即 a a1 a2 a3 ... an,并且 1 < a1…...
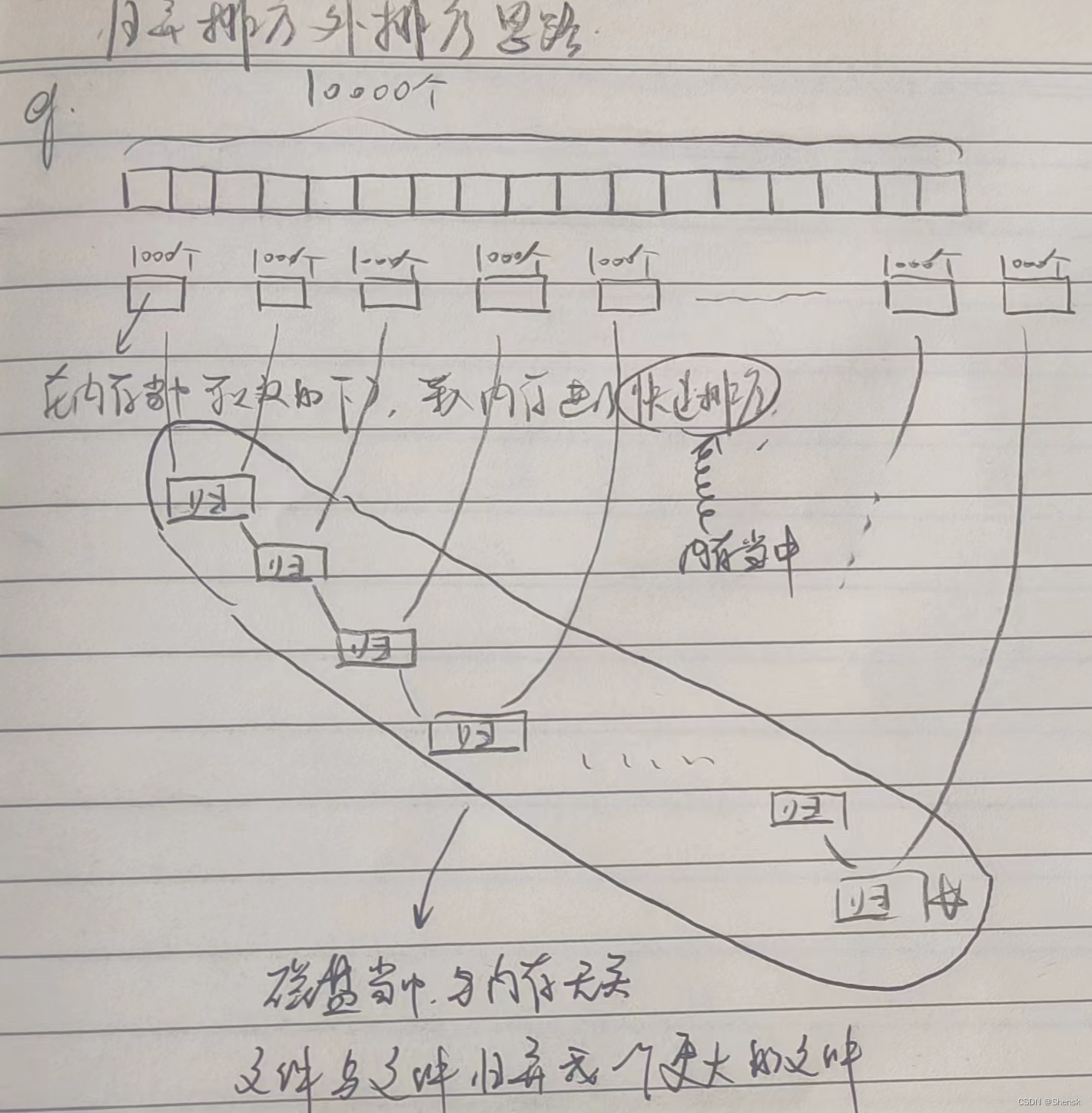
(排序10)归并排序的外排序应用(文件排序)
TIPS 在一些文件操作函数当中,fputc与fgetc这两个函数都是针对字符的,如果说你需要往文件里面去放入整形啊等等,不是字符的类型,这时候就用fprintf,fscanf在参数里面数据类型控制一下就可以。但是话说回来,…...
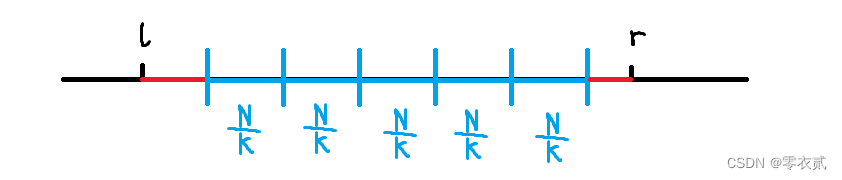
浅谈根号分治与分块
文章目录 1. 根号分治哈希冲突 2. 线性分块引入教主的魔法[CQOI2011] 动态逆序对[国家集训队] 排队[HNOI2010] 弹飞绵羊蒲公英 1. 根号分治 哈希冲突 题目1 n n n 个数, m m m 次操作。操作 1 为修改某一个数的值,操作 2 为查询所有满足下标模 x x x …...
(OpenAI)ChatGPT注册登录常见问题错误代码及其解决方法
在使用 ChatGPT 的时候我们可能会碰到一些错误的代码,本文统一来介绍一下每一种错误以及解决方法。 错误代码1. 不能在当前国家使用 出现场景:一般在注册或登录的时候会出现。 原因:主要是ChatGPT检测到当前访问所在的地区不允许访问导致。 …...
MySQL主从复制、读写分离(MayCat2)实现数据同步
文章目录 1.MySQL主从复制原理。2.实现MySQL主从复制(一主两从)。3.基于MySQL一主两从配置,完成MySQL读写分离配置。(MyCat2) 1.MySQL主从复制原理。 MySQL主从复制是一个异步的复制过程,底层是基于Mysql数…...

Linux 云服务器好用吗?(解读Linux云服务器的特点优势)
如今,云计算越来越受欢迎,许多公司正在将业务转移到那里。企业向云过渡的主要原因是它提供的众多服务,包括安全和充足的存储、数据库、服务器和其他关键元素。 作为相对前|沿的技术之一,云建立在虚拟服务器上。Linux 服务器…...
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理)
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理) matchother和占位符_区别 easy matchenum matchno valuematch inner Option matchmore better way if-let整洁控制包管理模块(mod)拆分声明modpub公开use展开引用拆解模块结…...

G8期刊《全体育》期刊简介及投稿要求
G8期刊《全体育》期刊简介及投稿要求 《全体育》是由湖南体育产业集团有限公司主管、体坛传媒集团股份有限公司主办、中教体育 出版发行的体育综合性期刊。 主管:湖南体育产业集团有限公司 主办:体坛传媒集团股份有限公司 国内刊号:CN4…...
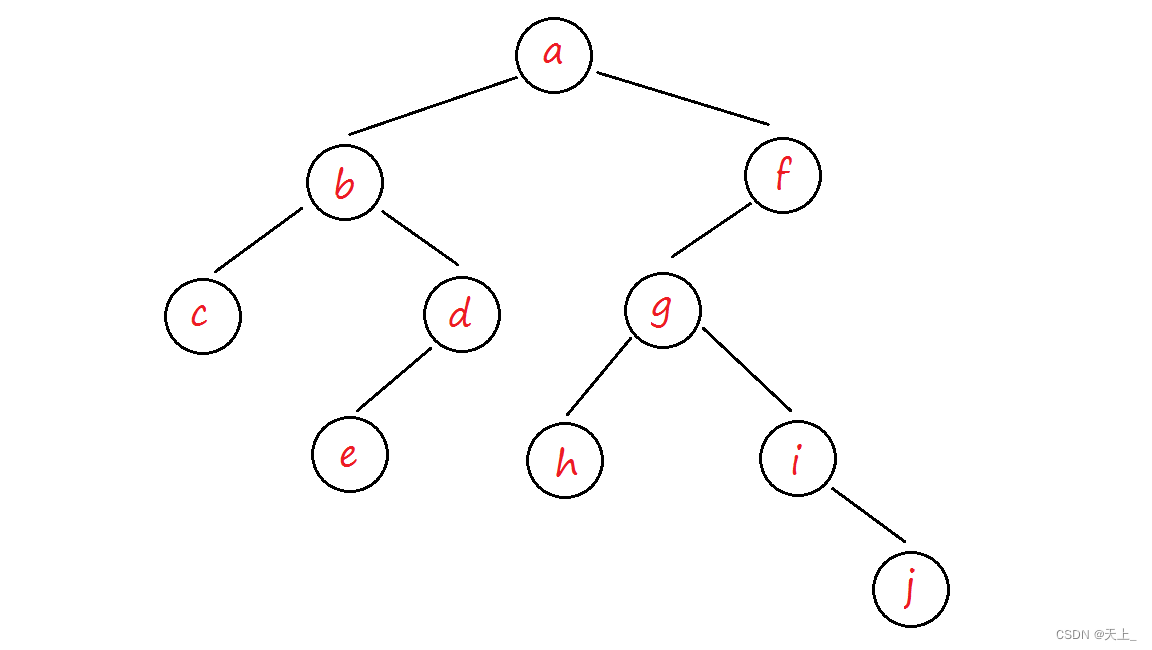
数据结构和算法学习记录——层序遍历(层次遍历)、二叉树遍历的应用(输出二叉树中的叶节点、求二叉树的高度、二元运算表达式树及其遍历、由两种遍历序列确定二叉树)
目录 层序遍历 思路图解 代码实现 二叉树遍历的应用 输出二叉树中的叶节点 代码实现 求二叉树的高度 思路图解 代码实现 二元运算表达式树及其遍历 由两种遍历序列确定二叉树 层序遍历 层序遍历可以通过一个队列来实现,其基本过程为: 先根…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
