(十七)排序算法-基数排序
1 基本介绍
1.1 概述
(1)基数排序(radix sort)属于“分配式排序”,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用。
(2)基数排序是属于稳定性的排序,基数排序法是效率高的稳定性排序法。
(3)基数排序是桶排序的扩展。
(4)基数排序是1887年赫尔曼.何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
1.2 算法详解
首先基数排序是根据数位来进行排序的。它是从个位开始,然后按照每一位的数进行排序,如下图所示:

排完序之后就往前进一位,然后再将所有的数按照这一位所在的数进行排序,如下图所示:

重复这个过程直到所有的位数都已经被排过序了。如下图所示:

并且如果这个过程中碰到某个数在这个为上没有数的话就进行补零操作,将该位看成是0。就比方下图用红框圈出来的部分:

等到所有的位数都已经排序完毕之后,就可以看到已经排序好的序列了。
这个过程很好理解,但是如果是第一次看这个算法的肯定会有一个的困惑,那就是为什么基数排序选择的是从低位到高位来进行排序的,而不是像平常比较数据的大小一样,从高位到低位来比较呢?
这里先不讲为什么,先看下面这两个案例:
- 从高位到低位进行比较
| 原序列 | 百位排好序后 | 十位排好序后 | 个位排好序后 |
|---|---|---|---|
| 329 | 839 | 657 | 839 |
| 457 | 720 | 457 | 329 |
| 657 | 657 | 355 | 657 |
| 839 | 457 | 839 | 457 |
| 436 | 436 | 436 | 436 |
| 720 | 329 | 720 | 355 |
| 355 | 355 | 329 | 720 |
- 从低位到高位进行比较
| 原序列 | 个位排好序后 | 十位排好序后 | 百位排好序后 |
|---|---|---|---|
| 329 | 720 | 720 | 329 |
| 457 | 355 | 329 | 355 |
| 657 | 436 | 436 | 436 |
| 839 | 457 | 839 | 457 |
| 436 | 657 | 355 | 657 |
| 720 | 329 | 457 | 720 |
| 355 | 839 | 655 | 839 |
对比看了上面两个例子之后相信大家就知道了,很明显,如果是从高到低位来进行比较的话,会发现比较到最后之后序列仍然是无序的,但是从低位到高位进行比较的话,就会发现序列到最后已经排好序了。
是不是很奇怪,同样的执行过程,只不过执行的顺序发生了改变,为什么结果就回产生这样的结果呢?产生这个差异的重点就是在我们忽略了一个问题,那就是在进行高位到低位比较的时候,高位的权重是高于低位的。就比方下图所示:

正是因为这个原因,所以采取的是从低位到高位比较的过程.
说完基本思想之后,来说一下算法的实现步骤:
- 第一次遍历序列.找出序列中的最大值MAX,找到MAX之后,可以确定,需要比较多少数位了。
- 这时候,就需要按照元素在该位数对应的数字将元素存入到相应的容器之中。如下图所示:

- 之后再按照容器的顺序将元素重新弹出,构成接下来需要排序的序列,如下图所示:

- 最后只需要重复2,3步骤,直到最高位也比较完毕,那么整个基数排序就已经完成了。
算法图解:

2 代码实现
/*** 基数排序*/
public class RadixSort {public static void main(String[] args) {int[] arr = {53, 3, 542, 478, 14, 241, 2, 23};radixSort(arr);System.out.println(Arrays.toString(arr));}// 基数排序方法public static void radixSort(int[] arr) {// 得到数组中最大的数的位数int max = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}// 得到最大数的位数,决定循环几轮int maxLength = (max + "").length();// 定义一个二维数组,表示10个桶,每个桶就是一个一维数组// 说明// 1. 二维数组包含10个一维数组// 2. 为了防止在放入数的时候,数据溢出,则每一个一维数组(桶),大小定为 arr.length// 3. 明确,基数排序是使用空间换时间的经典算法int[][] bucket = new int[10][arr.length];// 为了记录每个桶中,实际存放了多少个数据,定义一个一维数组来记录各个桶的每次放入的数据个数int[] bucketElementCounts = new int[10];// 循环 maxLength 轮for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {// 针对每个元素的对应位进行排序for (int j = 0; j < arr.length; j++) {// 取出每个元素的对应位的值int digitOfElement = arr[j] / n % 10;// 放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++;}// 按照这个桶的顺序,依次取出数据,放入到原来数组int index = 0;for (int k = 0; k < bucketElementCounts.length; k++) {// 如果桶中有数据,放入到原数组if(bucketElementCounts[k] != 0){// 循环该桶,即第k个桶,放入for (int l = 0; l < bucketElementCounts[k]; l++) {arr[index++] = bucket[k][l];}}// 第 i+1 轮处理后,需要将每个 bucketElementCounts[k]=0bucketElementCounts[k] = 0;}System.out.println("第" + (i+1) + "轮,对位数的排序处理 arr=" + Arrays.toString(arr));}}
}3 复杂度分析
- 时间复杂度
基数排序只需要根据最大元素的位数,遍历相应次数的序列即可,所以可以确定基数排序的时间复杂度一定是线性级别的,虽然是线性级别的,但是有一个系数的,这个系数就是最大元素的位数K,所以时间复杂度应该是O(n*k)。 - 空间复杂度
空间复杂度主要取决于链表的数量以及序列元素的数量,所以空间复杂度为O(n+k)。
相关文章:

(十七)排序算法-基数排序
1 基本介绍 1.1 概述 (1)基数排序(radix sort)属于“分配式排序”,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用。 (2&#x…...
详解)
JMM之先行发生原则(happens-before)详解
1、概述 在JMM规范下,如果一个操作执行的结果需要对另一个操作可见,那么这两个操作之间必须存在happers-before(先行发生)原则。 例如 int x 10 ; int y x; 这两行代码中第二个操作 yx ,因为需要将x值赋值给y,所以第一行代码的…...

含分布式电源的配电网可靠性评估研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

安全加固服务是什么?哪些行业需要做?
安全加固服务是什么?安全加固服务是一种针对企业信息系统、网络设备、应用程序等进行安全加固和优化的服务。安全加固服务的主要目的是保障企业信息系统的安全性和稳定性,有效防范各类网络攻击和安全威胁。 安全加固服务是什么?通常包括以下…...

好程序员:Java书籍推荐,程序员必看的5本Java书籍,赶紧收藏!
今天好程序员给大家推荐5本Java书籍,各大高校都在使用(具体名单如下),所有学习Java的程序员都不应该错过! 第一本Java书籍《Java EE(SSM框架)企业应用实战》 本书全面介绍了JavaEE中MyBatis、Sp…...
maven将jar包添加到本地仓库
第一步:下载需要添加的jar包 可以在maven库中查找下载,也可以在对应官网下载 maven库网址:https://mvnrepository.com/ 找到对应版本的jar包下载 第二步:将下载的jar包放到指定位置(位置自己指定)…...
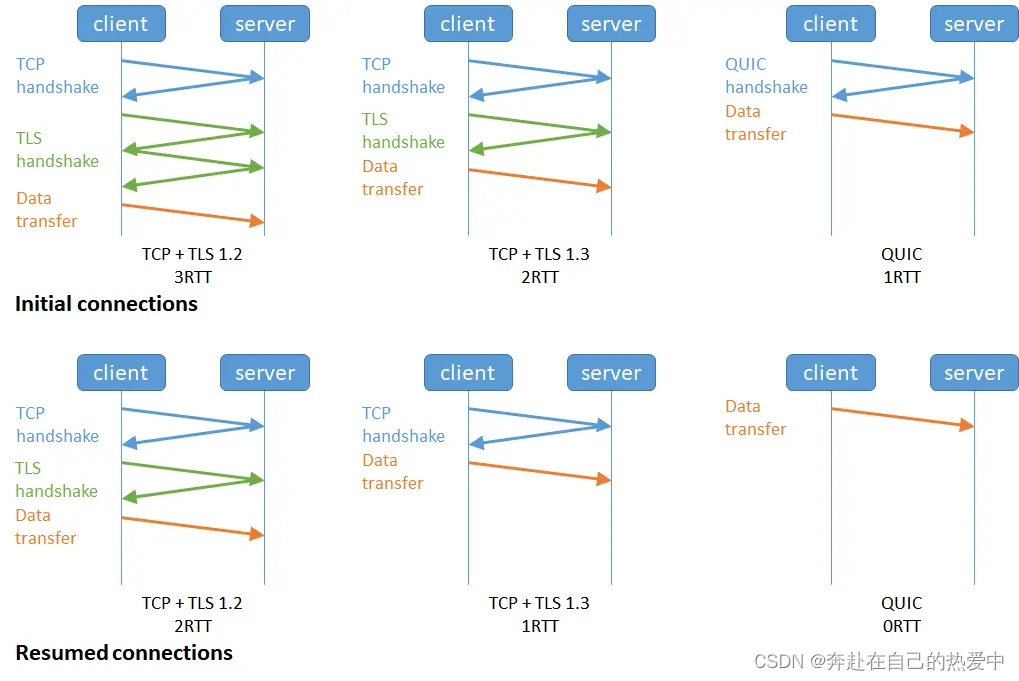
4.12--计算机网络之TCP篇之TCP 协议的缺陷+如何基于 UDP 协议实现可靠传输?--(复习+大总结)---沉下心来(加油呀)
TCP 协议四个方面的缺陷: 1.升级 TCP 的工作很困难; TCP 协议是在内核中实现的,应用程序只能使用不能修改,如果要想升级 TCP 协议,那么只能升级内核。 而升级内核这个工作是很麻烦的事情 2.TCP 建立连接的延迟&#x…...

数据库网络编程
数据库网络编程是一个重要的领域,它涉及到如何使用编程语言与数据库进行交互,以及如何设计和实现网络应用程序。在这篇文章中,我将探讨数据库网络编程的基础知识、常用技术和实践经验,以及一些应用案例和未来发展趋势。 一、基础…...

为什么现代企业都在使用ERP系统 它有哪些优势
随着科技的不断发展,企业管理方式也在不断地发生改变。在这个信息化的时代,企业要想取得成功,必须要善于利用先进的信息化技术工具。其中,ERP系统是企业管理中不可或缺的重要工具。本文将探讨现代企业为什么会使用ERP系统…...

别再用 BeanUtils 了,这款 PO VO DTO 转换神器不香么?
老铁们是不是经常为写一些实体转换的原始代码感到头疼,尤其是实体字段特别多的时候。介绍一个开源项目 mapstruct ,可以轻松优雅的进行转换,简化你的代码。当然有的人喜欢写get set,或者用BeanUtils 进行复制,代码只是…...
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数
LeetCode算法小抄-- 最近公共祖先 和 完全二叉树的节点个数 最近公共祖先[236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)[235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-b…...
)
php、redis实现分布式锁的正确写法(原子操作 通用类 加讲解)
最终代码(通用类) 1 面试中、实际工作中,经常涉及到 redis 分布式锁,正确写法如下。先奉上代码,再讲解。 <?php namespace app\common\library; /*** 通用分布式锁(原子操作)*/ class Lock {/*** 获取redis实例* return \Redis* throws…...
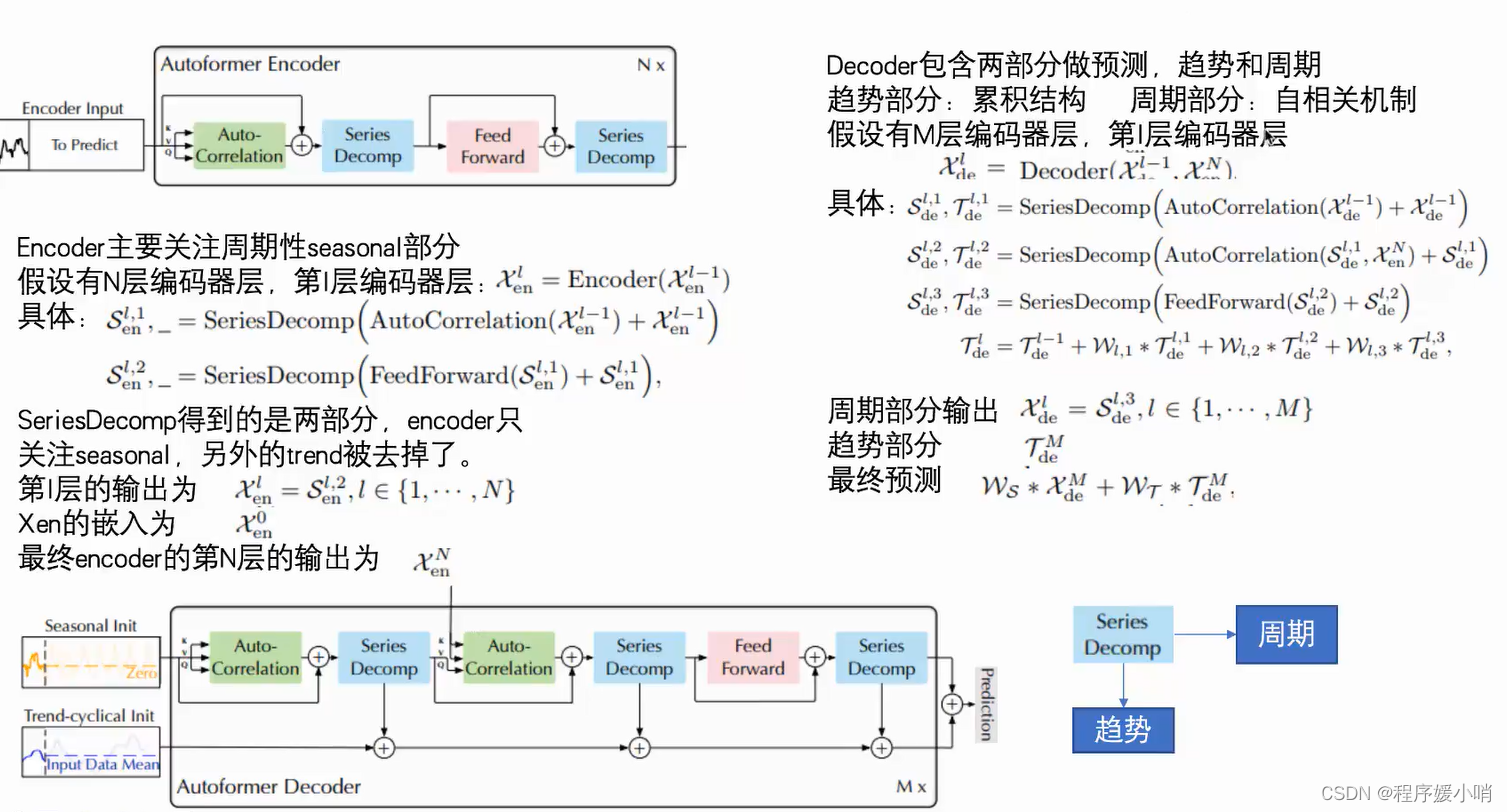
Transformer在时序预测的应⽤第一弹——Autoformer
Transformer在时序预测的应⽤第一弹——Autoformer 原文地址:Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting(NIPS 2021) 做长时间序列的预测 Decomposition把时间序列做拆分,…...
文章改写神器在线-AI续写文章生成器
AI续写生成器 AI续写生成器是一种利用人工智能技术的创意工具,能够提高写作效率,为营销推广带来全新的可能性。无论你是写手、广告人员还是市场营销人员,这个工具都能够有效地解决你在写作中遇到的难题。 在内容创作行业中,原创…...
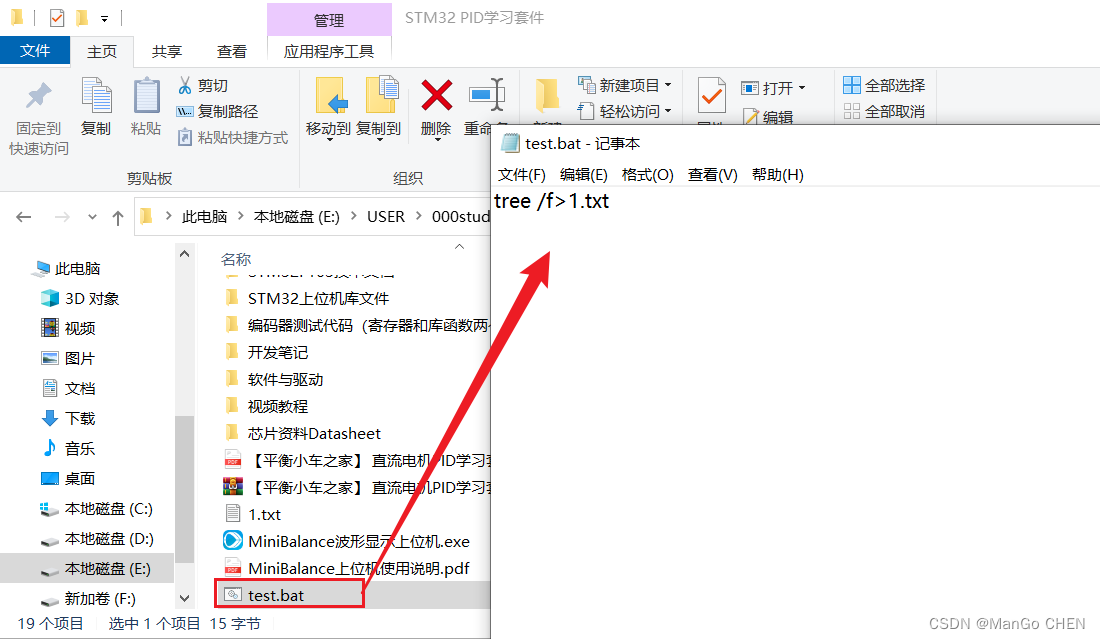
一秒钟给硬盘文件做个树状结构目录
一秒钟给硬盘文件做个树状结构目录 一、背景 对于长时间坐在电脑前的打工人来说,若没有养成良好文件分类习惯的话,年终整理电脑文件绝对是件头疼的事情。 给磁盘文件做个目录,一目了然文件都在哪里?想想都是件头疼的事情。 对于…...
电脑重装系统后会怎样?
有小伙伴的电脑系统运行缓慢卡顿,现在想通过重装系统来解决问题。咨询电脑重装系统会怎么样对系统有影响吗,现在小编就带大家看看电脑重装系统后会怎样。 方法/步骤: 一、电脑重装系统会怎么样 1、我们的电脑重装系统后,电脑…...

100种思维模型之反熵增思维模型-47
查理芒格被誉为反熵增思维模型的倡导者。本文将介绍查理芒格的反熵增思维模型,并分析它的实用性。 一、什么是熵增? 在物理学中,熵是衡量系统无序程度的指标。系统的熵越高,其无序程度越高。这个概念也可以应用到其他领域。在金融…...
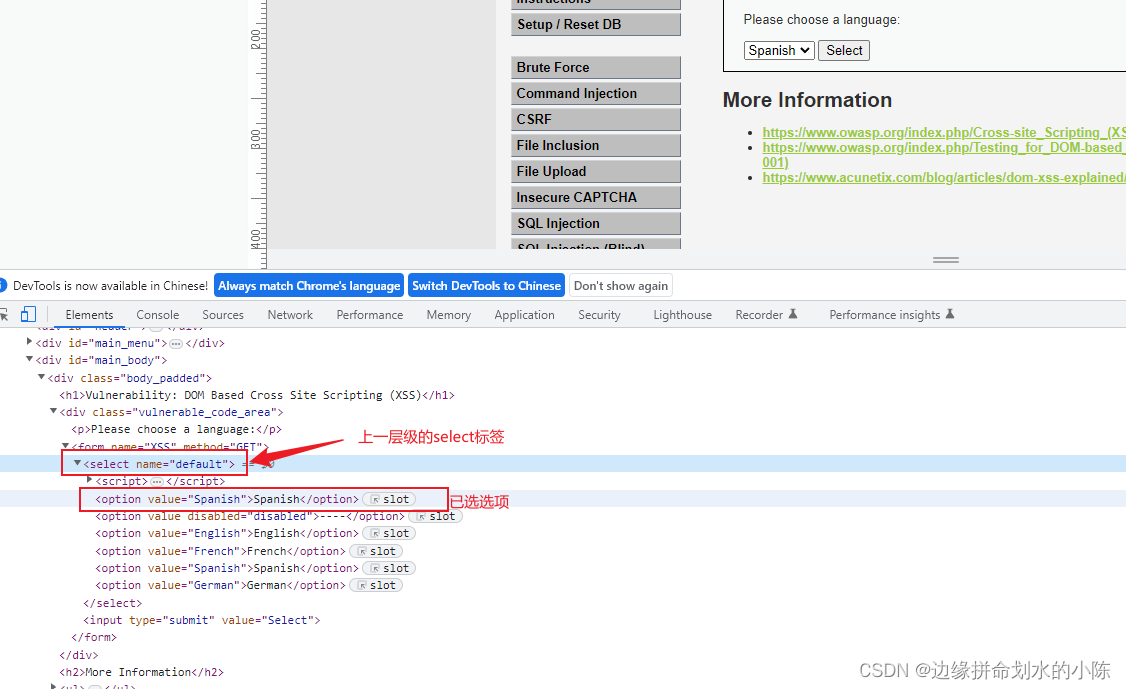
【网络安全】Xss漏洞
xss漏洞 xss漏洞介绍危害防御方法xss测试语句xss攻击语句1. 反射性xss2.存储型xss3.DOM型xssdvwa靶场各等级渗透方法xss反射型(存储型方法一致)LowMediumHightimpossible Dom型LowMediumHight xss漏洞介绍 定义:XSS 攻击全称跨站脚本攻击&am…...
17.网络爬虫—Scrapy入门与实战
这里写目录标题 Scrapy基础Scrapy运行流程原理Scrapy的工作流程Scrapy的优点 Scrapy基本使用(豆瓣网为例)创建项目创建爬虫配置爬虫运行爬虫如何用python执行cmd命令数据解析打包数据打开管道pipeline使用注意点 后记 前言: 🏘️🏘️个人简介…...

【面试题】JavaScript 中 try...catch 的使用技巧 ?
大厂面试题分享 面试题库 前后端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 web前端面试题库 VS java后端面试题库大全 作为一位 Web 前端工程师,JavaScript 中的 try...catch 是我们常用的特性之一。…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
