【LeetCode 图论 一】初探有向图Directed Graph
今天主要介绍DAG (Directed acyclic graph),有向无环图。
无向图的问题相对有向图比较简单,比如岛屿问题,迷宫问题等。
在有向图中,我们通常只关注环是否存在,因为有向图中环的存在会让我们的程序陷入死循环。
举个例子,有向图中的方向通常指代一些事情的执行顺序,比如说[a, b], [b, c]
我们假设a,b,c是三门课程,要学左边的课程之后才能学右边的课程,所以这里我们如果要学c,就要先学a,再学b,最后才能学c。
那如果有环,【a,b】,【b,a】,显然这是矛盾的。
同样。对于一些列复杂的课程
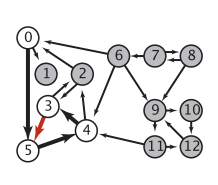
若我们想学5,则要先学3,要学3则要先学4,而要学4则要先学5…这无解
这会让我们DFS的搜索陷入循环。
所以一般我们进行搜索的时候,需要判断环是否存在。
另外我们还要提一下【拓扑排序】
刚刚的课程选择问题中,是一种优先级限制下的调度问题,在有向图中它的定义是
在满足限制条件的情况下如何安排并完成所有任务。
我们可以画出一张有向图,顶点对应任务(通过数组索引来表示课程),有向边对应优先级顺序。
而有向图中的优先级限制下的调度问题,等价于【拓扑排序】,它的定义是:
给定一副有向图,将所有的顶点排序,使得所有的有向边均从排在前面的顶点指向排在后面的顶点。 如下图
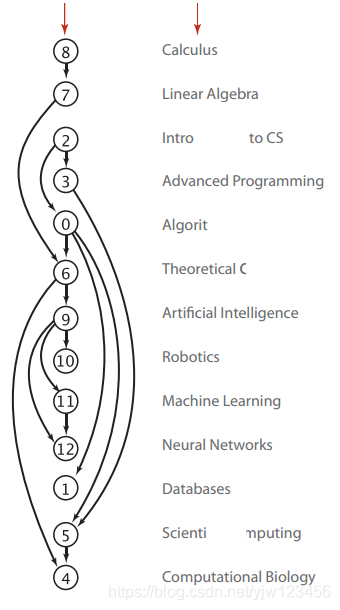
同学可以按照上面排序之后的有向图修完所有课程。
我们利用DFS寻找环:
维护一个递归调用期间已访问的顶点的栈Stack,若(在递归调用期间,通过判断onStack标记数组)两次访问了某个顶点,则说明有环;若DFS递归调用完毕,说明无环。
上面说的还是比较抽象。但是已经大致有一个印象了,就是,有向无环图因为它的顺序限制原因,已经搜索完的点,是不可能再次回到它这里的。
具体的,我们参考上面拓扑排序的图,当搜索到某个点,它没有相邻节点,它就入栈。
所以最终结果是,我们将 最后的课程4放在了栈底,最初的课程8放在栈的最顶部。
由于搜索是从随机的点开始的,我们将没有相邻节点的点入栈之后,再回溯到初始节点,将它入栈,但是后面的搜索也可能会碰到它。所以要给已经搜索的节点打上标签。
另外要注意一点,有些情况下会提示图中无环,但是有些题目不会提示,所以我们考虑一下再搜索过程中判断是否有环,具体的,对于某些节点X,我们搜索过,但是因为我们还没找到那个没有相邻节点的点end,或者我们还没有从end回溯到X,那么此时X节点的状态就是【搜索中】,如果我们搜索的过程中,两次搜索到X,那说明到X节点的图不是单向的,而是存在一个环。
所以,我们将节点分类为【搜索中】【已搜索】【未搜索】
假设有一对相邻节点(u,v),方向是u到 v 。
我们从u开始搜索,此时需要判断v的状态
【v是未搜索】:那我们可以搜索v,搜索完成之后,回溯到u 。
【v是搜索中】:那表示有一个环经过了v节点,这种情况下不存在拓扑排序。
【v是已搜索】:那v已经入栈了,而u不在栈中,那么u入栈就和v没关系,只看u自己的其他相邻节点来决定它的入栈时间即可。
下面用题目演示更直白
LeetCode 210 课程表II
https://leetcode.cn/problems/course-schedule-ii/
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。
给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,
表示在选修课程 ai 前 必须 先选修 bi 。例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。实例1
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。实例2
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。实例3
输入:numCourses = 1, prerequisites = []
输出:[0]
import collections
class Solution:def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]: edges = collections.defaultdict(list) # 有向图的表达方式for x in prerequisites:edges[x[1]].append(x[0]) # 每个点 和 它能到的相邻节点has_circle = False #是否包含环res = [] # 栈底是没有相邻节点的点,栈顶是源点,返回res[::-1]state = [0]*numCourses# 0 1 2 代表未搜索 搜索中,已搜索def dfs(current):nonlocal has_circle # nonlocal:函数之外定义,函数之内改变值state[current]=1for v in edges[current]:if state[v] ==1:has_circle=Truereturnelif state[v] ==0:dfs(v)if has_circle:returnelse:continue state[current]=2 # 每次的dfs会添加一个节点到栈底,这个节点没有指向任何节点res.append(current)for i in range(numCourses):if not has_circle and not state[i]:dfs(i)if has_circle:return []return res[::-1]
LeetCode 207 课程表
https://leetcode.cn/problems/course-schedule/
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。示例 1:输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。解答方法就是判断这个有向图中有没有环。比上一题更简单。
class Solution:def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:# 不能完成的几个情况 # 图中有环,自相矛盾import collectionsedges = collections.defaultdict(list)for x in prerequisites:edges[x[1]].append(x[0])state = [0]*numCourses # 0 1 2 未搜索 搜索中 已搜索has_circle = False# res_stack = []def dfs(u):nonlocal has_circlestate[u]=1for v in edges[u]:# print(v, state)if state[v]==0:dfs(v)if has_circle:return elif state[v] ==1:has_circle=Truereturnelse:continuestate[u]=2# res_stack.append()for i in range(numCourses):if not has_circle and not state[i]:dfs(i)if has_circle:return Falsereturn True相关文章:

【LeetCode 图论 一】初探有向图Directed Graph
今天主要介绍DAG (Directed acyclic graph),有向无环图。 无向图的问题相对有向图比较简单,比如岛屿问题,迷宫问题等。 在有向图中,我们通常只关注环是否存在,因为有向图中环的存在会让我们的…...

计算机视觉:图片数据的预处理
本文重点 图片数据是计算机视觉处理的核心,一般的图片数据并不能直接放到神经网络中,而是应该使用一些数据与处理的方式来解决,这个操作我们称为图片数据的预处理。 图像缩放 图像缩放是指将图像的尺寸调整为所需的大小。在AI中,图像缩放通常用于将图像调整为模型所需的…...

探秘C++中的神奇组合:std--pair的魅力之旅
探秘C中的神奇组合:std::pair的魅力之旅 引言std::pair简介及基本概念(An Overview and Basic Concepts of std::pair)std::pair的结构及构造方法(Structure and Construction Methods of std::pair)std::pair的常用成…...
Win10搭建我的世界Minecraft服务器「内网穿透远程联机」
文章目录 1. Java环境搭建2.安装我的世界Minecraft服务3. 启动我的世界服务4.局域网测试连接我的世界服务器5. 安装cpolar内网穿透6. 创建隧道映射内网端口7. 测试公网远程联机8. 配置固定TCP端口地址8.1 保留一个固定tcp地址8.2 配置固定tcp地址 9. 使用固定公网地址远程联机 …...

基于springboot和ajax的简单项目 02 代码部分实现,xml文件sql语句优化 (中)
上次说到了log/log_list.html的doGetObjects(),其中有doFindPageObjects()方法。 找到全部的日志对象,并且输出到div上。这里是后台的代码。 01.pojo对象,这里需要序列化保存。序列化的作用是保存对象到内存缓存中&am…...

LNMP架构部署
L:Linux A:Apache M:Mysql P:PHP 各组件的主要作用如下: (平台)Linux:作为LAMP架构的基础,提供用于支撑Web站点的操作系统,能够与其他三个组件提供更好的稳定性,兼容性(AMP组件也支持Windows、UNIX等平…...
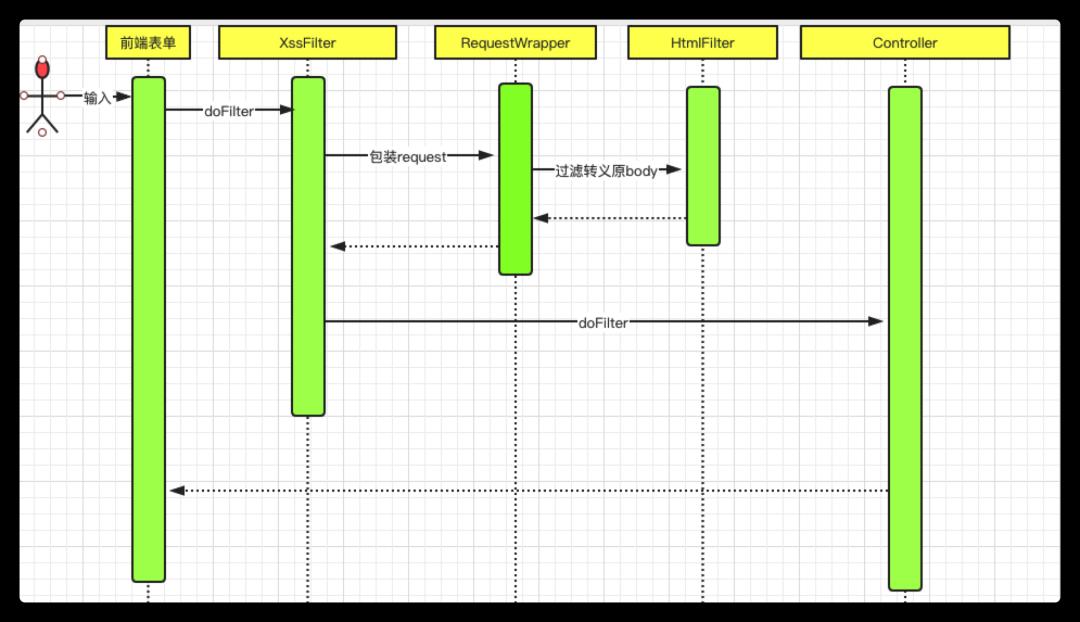
SpringBoot 防护XSS攻击
目录 一、前言 1.1、XSS攻击流程 1.2、XSS攻击分类 1.3、攻击方式 二、解决方案 2.1、SPRINGBOOT XSS过滤插件(MICA-XSS) 2.2、MICA-XSS 配置 三、项目实战 3.1、项目环境 3.2、测试 3.2.1、测试GET请求 3.2.2、测试POST请求 3.2.3、测试POS…...

iOS 吸顶效果
项目中,在列表向上滚动时,有时需要将某个控件置顶,这就是我们常见的吸顶效果。 1. UITableView 吸顶效果 UITableView是自带吸顶效果,我们把需要置顶的控件设置为SectionHeaderView,这样在滚动时,该控件会…...

文本翻译免费软件-word免费翻译软件
好用的翻译文件软件应该具备以下几个方面的特点:支持多种文件格式,翻译结果准确可靠,界面操作简便易用,价格实惠,用户体验舒适。以下是几个好用的翻译文件软件: 1.147cgpt翻译软件 翻译软件特点࿱…...
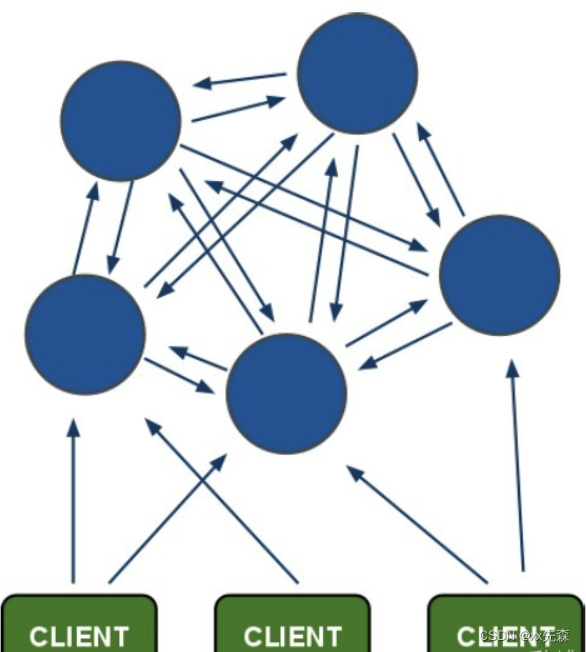
redis 主从模式、哨兵模式、cluster模式的区别
参考: https://blog.csdn.net/qq_41071876/category_11284995.html https://blog.csdn.net/weixin_45821811/article/details/119421774 https://blog.csdn.net/weixin_43001336/article/details/122816402 Redis有三种模式,分别是:主…...
SDL(2)-加载图片
加载BMP 1.使用SDL_init初始化SDL库 2.使用SDL_CreateWindow创建一个窗口 3.使用SDL_GetWindowSurface获取创建窗口的surface 4.使用SDL_LoadBMP加载一张BMP图片 5.使用SDL_BlitSurface将加载的bmp surface拷贝到窗口的surface 6.使用SDL_UpdateWindowSurface更新到窗口 …...

指针数组和数组指针
指针和数组都是C语言中非常重要的概念。它们各自有其用途和应用场景。本文将介绍指针数组和数组指针,两者的区别和用法。 指针数组 指针数组是指一个数组,其中的每个元素都是一个指针类型。例如,下面这个定义了3个字符型指针的数组…...

程序员最常见的谎言
小伙伴们大家好,我是阿秀。 上周看到知乎上有位网友总结了自己的10年程序员生涯中最常说的一些谎言,一共有15条,看完我直呼内行!! 全中!每一枪都中了!每一条我都说过。 我基本都说过他说过的那些…...

hypothesis testing假设检验
假设检验是什么 比如一家巧克力工厂生产的巧克力每个1g,一个工人说,机器在维修之后生产的巧克力不是1g,为了验证工人说的是否正确,需进行假设检验。 随机挑选50个巧克力,计算平均重量。 H0:每个巧克力1g H…...
ChatGPT扩展系列之解决ChatGPT 被大面积封号的终极方案
ChatGPT扩展系列之解决ChatGPT 被大面积封号的终极方案 本节介绍了一个解决ChatGPT在中国大陆无法使用和担心被封号的问题的方法。近期有很多亚洲用户被封号,原因是有人滥用API接口或者批量注册账号,不符合官方规定。对于这个问题,提出了一个解决方法,可以在中国大陆无需翻…...
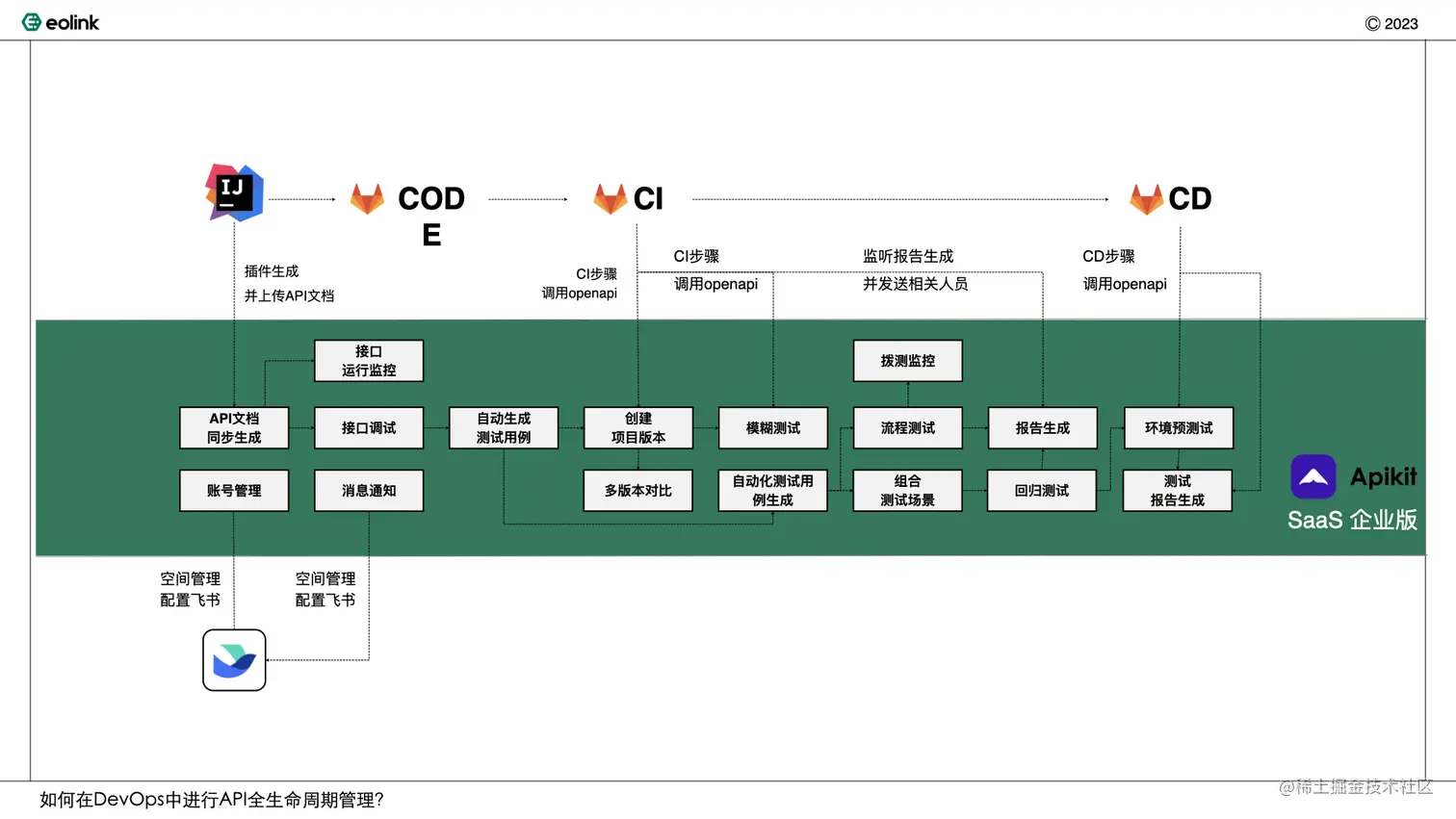
如何在DevOps中进行API生命周期管理?
引言 随着DevOps理念在中国企业当中的普及和发展,中国企业DevOps落地成熟度不断提升,根据中国信通院的数据已有近6成企业向全生命周期管理迈进。而在研发全生命周期管理之中,API管理的地位愈发显得重要。随着API数量的大幅增长,也…...
嵌套列表,与摩尔投票进阶
title: “Python fishC 22” author: “hou wei” date: “2023-04-16” output: html_document knitr::opts_chunk$set(echo TRUE)问答题 0.请问 运算符和 is 运算符有什么区别呢? 在Python中运算符用于比较两个变量的值是否相等,而is运算符用于判断…...
ChatGPT原理解释
写了一本介绍ChatGPT原理的课程 结构如下 01、介绍ChatGPT及其原理 1.1 ChatGPT的概述 1.2 什么是自然语言处理(NLP) 1.3 深度学习与NLP的关系 1.4 GPT模型的介绍 02、GPT原理探讨 2.1 GPT模型的输入与输出 2.2 GPT模型的结构 2.3 GPT模型的预训练方法…...
【配电网故障重构SOP】基于二阶锥松弛的加光伏风机储能进行的配电网故障处理和重构【考虑最优潮流】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

ajax 的入门案例
一、ajax ajax,Asynchronous JavaScript And XML,异步的JavaScript和XML 同步:伴随着页面的刷新或跳转,即全局刷新;同步请求会阻塞代码的执行,即同步请求会一个一个的执行 异步:在不刷新页面…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
