牛顿法、梯度下降法与拟牛顿法
牛顿法、梯度下降法与拟牛顿法
- 0 引言
- 1 关于泰勒展开式
- 1.1 原理
- 1.2 例子
- 2 牛顿法
- 2.1 x 为一维
- 2.2 x 为多维
- 3 梯度下降法
- 4 拟牛顿法
- 4.1 拟牛顿条件
- 4.2 DFP 算法
- 4.3 BFGS 算法
- 4.4 L-BFGS 算法
0 引言
机器学习中在求解非线性优化问题时,常用的是梯度下降法和拟牛顿法,梯度下降法和拟牛顿法都是牛顿法的一种简化
牛顿法是在一个初始极小值点做二阶泰勒展开,然后对二阶泰勒展开式求极值点,通过迭代的方式逼近原函数极值点
在牛顿法迭代公式中,需要求二阶导数,而梯度下降法将二阶导数简化为一个固定正数方便求解
拟牛顿法也是在求解过程中做了一些简化,不用直接求二阶导数矩阵和它的逆
1 关于泰勒展开式
1.1 原理
如果我们有一个复杂函数 f ( x ) f(x) f(x), 对这个复杂函数我们想使用 n 次多项式(多项式具有好计算,易求导,且好积分等一系列的优良性质)去拟合这个函数,这时就可以对 f ( x ) f(x) f(x)进行泰勒展开,求某一点 x 0 x_0 x0附近的 n 次多项式:
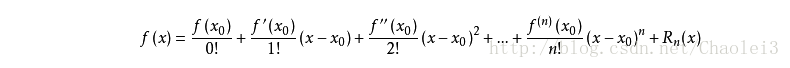
注意:
n 次多项式只是在 x 0 x_0 x0 较小的邻域内能较好拟合 f ( x ) f(x) f(x),也就是说,泰勒展开式其实是一种局部近似的方法,只近似 x = x 0 x=x_0 x=x0那一点的函数性
1.2 例子
现在要求 f ( x ) = c o s ( x ) f(x)=cos(x) f(x)=cos(x) 在 x 0 = 0 x_0=0 x0=0 处的二阶泰勒展开,因为我们去掉了高阶项,所以只是近似
直接套用公式
f ( x 0 ) = f ( 0 ) = c o s ( 0 ) = 1 f(x_0)=f(0)=cos(0)=1 f(x0)=f(0)=cos(0)=1
f ′ ( x 0 ) = f ′ ( 0 ) = − s i n ( 0 ) = 0 f'(x_0)=f'(0)=-sin(0)=0 f′(x0)=f′(0)=−sin(0)=0
f ′ ′ ( x 0 ) = f ′ ′ ( 0 ) = − c o s ( 0 ) = − 1 f''(x_0)=f''(0)=-cos(0)=-1 f′′(x0)=f′′(0)=−cos(0)=−1
所以展开后的公式为
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ∗ x + f ′ ′ ( x 0 ) ∗ x 2 / 2 = 1 − 0.5 ∗ x 2 f(x)≈f(x_0)+f'(x_0)*x+f''(x_0)*x^2/2=1-0.5*x^2 f(x)≈f(x0)+f′(x0)∗x+f′′(x0)∗x2/2=1−0.5∗x2
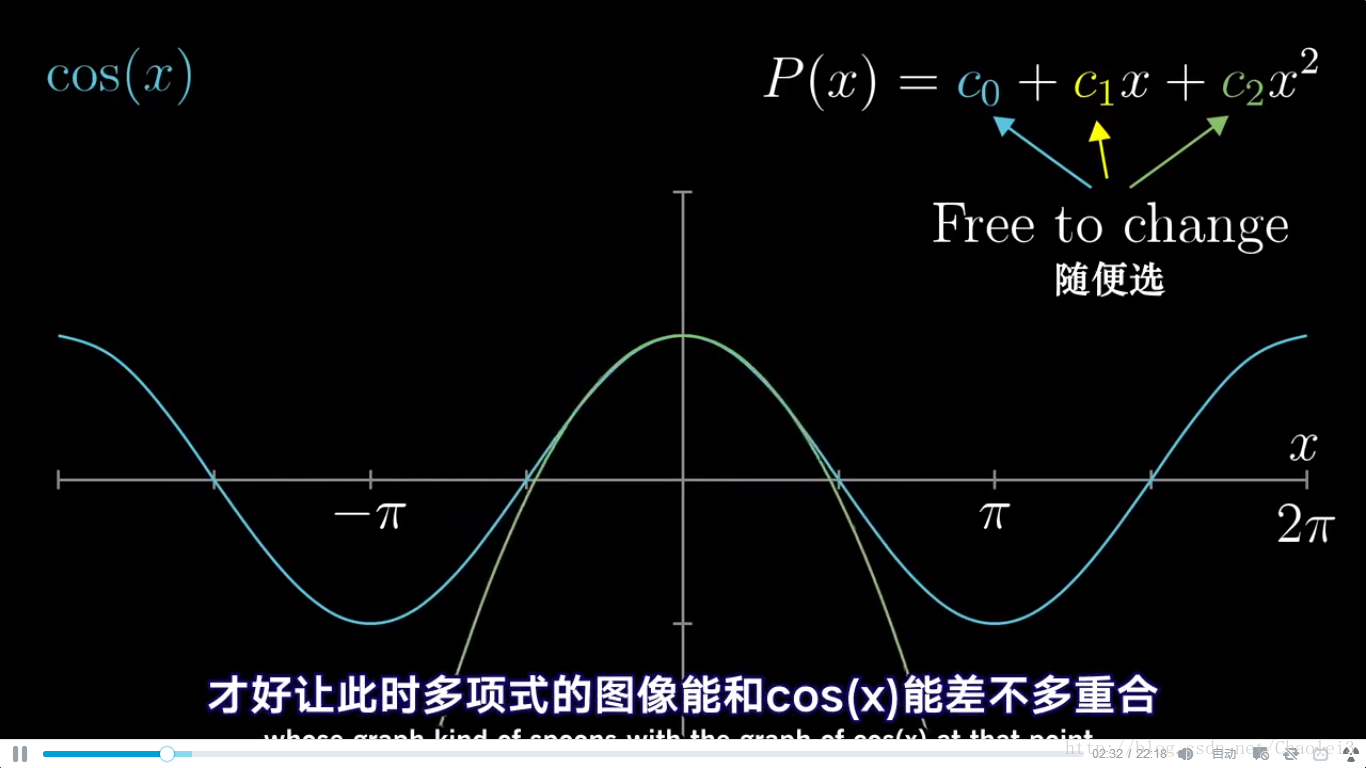
从下方运行程序可以看出,离展开点越近的点,拟合程度越高,越远的点,越离谱
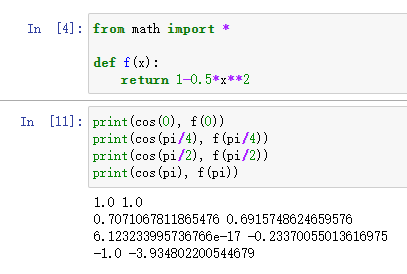
2 牛顿法
2.1 x 为一维
现在假设我们有目标函数 f ( x ) f(x) f(x),我们希望求此函数的极小值,牛顿法的基本思想是:随机找到一个点设为当前极值点 x k x_k xk,在这个点对 f ( x ) f(x) f(x) 做二次泰勒展开,进而找到极小点的下一个估计值。在 x k x_k xk 附近的二阶泰勒展开为:
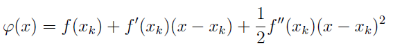
现在想求 φ ( x ) \varphi(x) φ(x) 的极值点,由极值的必要条件可知, φ ( x ) \varphi(x) φ(x) 应满足导数为 0,即:
φ ′ ( x ) = 0 \varphi'(x)=0 φ′(x)=0
即
φ ′ ( x ) = f ′ ( x k ) + f ′ ′ ( x k ) ( x − x k ) = 0 \varphi'(x)=f'(x_k)+f''(x_k)(x-x_k)=0 φ′(x)=f′(xk)+f′′(xk)(x−xk)=0
这样就可以求得 x 的值
x = x k − f ′ ( x k ) f ′ ′ ( x k ) x=x_k-\frac{f'(x_k)}{f''(x_k)} x=xk−f′′(xk)f′(xk)
于是给定初始值 x 0 x_0 x0,就可以通过迭代的方式逼近 f ( x ) f(x) f(x)的极值点:
x k + 1 = x k − f ′ ( x k ) f ′ ′ ( x k ) x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)} xk+1=xk−f′′(xk)f′(xk)
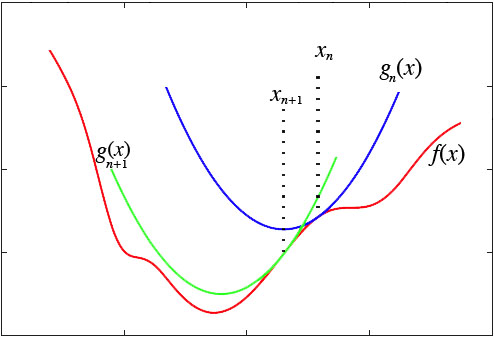
如下图,首先在 x n x_n xn 处泰勒展开,得到 f ( x ) f(x) f(x) 的近似函数 g n ( x ) g_n(x) gn(x) ,求得 g n ( x ) g_n(x) gn(x) 的极值点 x n + 1 x_{n+1} xn+1
随后在 x n + 1 x_{n+1} xn+1 出泰勒展开,得到 g n + 1 ( x ) g_{n+1}(x) gn+1(x) 函数,继续求 g n + 1 ( x ) g_{n+1}(x) gn+1(x) 的极值点
一直迭代最后就会逼近 f ( x ) f(x) f(x) 的极值点
2.2 x 为多维
上面讨论的是参数 x 为一维的情况,当 x 有多维时,二阶泰勒展开式可以做推广,此时:
φ ( x ) = f ( x k ) + ∇ f ( x k ) ∗ ( x − x k ) + 1 2 ∗ ( x − x k ) T ∗ ∇ 2 f ( x k ) ∗ ( x − x k ) \varphi(x)=f(x_k)+\nabla{f(x_k)}*(x-x_k)+ \frac{1}{2}*(x-x_k)^T*\nabla^2{f(x_k)}*(x-x_k) φ(x)=f(xk)+∇f(xk)∗(x−xk)+21∗(x−xk)T∗∇2f(xk)∗(x−xk)
其中 ∇ f \nabla{f} ∇f为 f f f 的梯度向量, ∇ 2 f \nabla^2{f} ∇2f为 f f f的海森矩阵(Hessian matrix),其定义为:
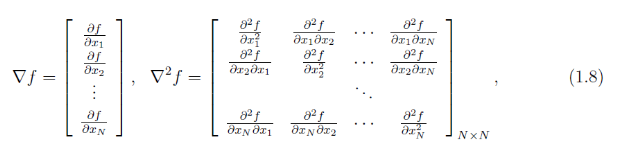
φ ( x ) \varphi(x) φ(x)对 x 向量求导并令其为 0 有:
∇ f ( x k ) + ∇ 2 f ( x k ) ∗ ( x − x k ) = 0 \nabla{f(x_k)}+\nabla^2{f(x_k)}*(x-x_k)=0 ∇f(xk)+∇2f(xk)∗(x−xk)=0
于是有:
x = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) x=x_k-[\nabla^2{f(x_k)}]^{-1}\nabla{f(x_k)} x=xk−[∇2f(xk)]−1∇f(xk)
通过迭代的方式能找到函数的极值点
牛顿法缺点:
- 函数必须具有一二阶偏导数,海森矩阵必须正定
- 计算相当复杂,除梯度外还需要计算二阶偏导数和逆矩阵
3 梯度下降法
在一维牛顿法中,迭代公式为:
x k + 1 = x k − f ′ ( x k ) f ′ ′ ( x k ) x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)} xk+1=xk−f′′(xk)f′(xk)
这个公式缺点:
- 需要求二阶导数,有些函数求二阶导数之后就相当复杂了;
- 因为 f ′ ′ ( x n ) f''(x_n) f′′(xn)的大小不定,所以 g ( x ) g(x) g(x)开口方向不定,我们无法确定最后得到的结果究竟是极大值还是极小值
为了解决这两个问题,我们放弃二阶精度,即去掉 f ′ ′ ( x n ) f''(x_n) f′′(xn),改为一个固定的正数1/h:
φ ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + 1 2 h ( x − x k ) 2 \varphi(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2h}(x-x_k)^2 φ(x)=f(xk)+f′(xk)(x−xk)+2h1(x−xk)2
该抛物线是一条开口向上的抛物线,通过求它的极值可以保证得到的是极小值。 φ ( x ) \varphi(x) φ(x) 的极小值点为
x k − h f ′ ( x k ) x_k-hf'(x_k) xk−hf′(xk)
迭代公式为
x k + 1 = x k − h f ′ ( x k ) x_{k+1} = x_k-hf'(x_k) xk+1=xk−hf′(xk)
对于高维空间就是
x k + 1 = x k − h ∇ ( x k ) x_{k+1} = x_k-h\nabla(x_k) xk+1=xk−h∇(xk)
4 拟牛顿法
拟牛顿法的基本思想是:不用二阶偏导数而构造出可以近似海森矩阵的正定对称阵,在“拟牛顿”的条件下优化目标函数。不同的构造方法就产生了不同的拟牛顿法。
一些记号:
∇ f \nabla{f} ∇f 记为 g 表示梯度, g k g_k gk表示 ∇ f ( x k ) \nabla{f(x_k)} ∇f(xk)
∇ 2 f \nabla^2{f} ∇2f 海森矩阵,记为 H, K k K_k Kk表示 ∇ 2 f ( x k ) \nabla^2{f(x_k)} ∇2f(xk)
用 B 表示对海森矩阵 H 本身的近似,D表示对海森矩阵的逆 H − 1 H^{-1} H−1的近似, 即 B ≈ H , D ≈ H − 1 B≈H, D≈H^{-1} B≈H,D≈H−1
4.1 拟牛顿条件
在经过 k+1 次迭代后得到 x k + 1 x_{k+1} xk+1,此时目标函数 f ( x ) f(x) f(x)在 x k + 1 x_{k+1} xk+1处作泰勒二阶展开,得到:
f ( x ) ≈ f ( x k + 1 ) + ∇ f ( x k + 1 ) ∗ ( x − x k + 1 ) + 1 2 ∗ ( x − x k + 1 ) T ∗ ∇ 2 f ( x k + 1 ) ∗ ( x − x k + 1 ) f(x)≈f(x_{k+1})+\nabla{f(x_{k+1})}*(x-x_{k+1})+ \frac{1}{2}*(x-x_{k+1})^T*\nabla^2{f(x_{k+1})}*(x-x_{k+1}) f(x)≈f(xk+1)+∇f(xk+1)∗(x−xk+1)+21∗(x−xk+1)T∗∇2f(xk+1)∗(x−xk+1)
两边对 x 求梯度有:
∇ f ( x ) ≈ ∇ f ( x k + 1 ) + H k + 1 ∗ ( x − x k + 1 ) (1) \nabla{f(x)} ≈ \nabla{f(x_{k+1})}+H_{k+1}*(x-x_{k+1}) \tag{1} ∇f(x)≈∇f(xk+1)+Hk+1∗(x−xk+1)(1)
在式(1)中取 x = x k x=x_k x=xk ,整理可得:
g k + 1 − g k ≈ H k + 1 ∗ ( x k + 1 − x k ) (2) g_{k+1}-g_{k}≈H_{k+1}*(x_{k+1}-x_k)\tag{2} gk+1−gk≈Hk+1∗(xk+1−xk)(2)
引入记号:
s k = x k + 1 − x k , y k = g k + 1 − g k s_k=x_{k+1}-x_k,y_k=g_{k+1}-g_{k} sk=xk+1−xk,yk=gk+1−gk
式 (2) 可以写为:
y k ≈ H k + 1 ∗ s k = > 简记为: y k ≈ B k + 1 ∗ s k y_k≈H_{k+1}*s_k =>简记为:y_k≈B_{k+1}*s_k yk≈Hk+1∗sk=>简记为:yk≈Bk+1∗sk
或者
s k ≈ H k + 1 − 1 ∗ g k = > 简记为: s k ≈ D k + 1 ∗ y k s_k≈H^{-1}_{k+1}*g_k=>简记为:s_k≈D_{k+1}*y_k sk≈Hk+1−1∗gk=>简记为:sk≈Dk+1∗yk
这就是所谓的拟牛顿条件,它对迭代过程中的海森矩阵做约束。
4.2 DFP 算法
参考:牛顿法与拟牛顿法学习笔记(三)DFP 算法
4.3 BFGS 算法
参考:牛顿法与拟牛顿法学习笔记(四)BFGS 算法
4.4 L-BFGS 算法
牛顿法与拟牛顿法学习笔记(五)L-BFGS 算法
参考:
泰勒展开式的理解
牛顿法与拟牛顿法学习笔记(一)牛顿法
梯度下降和EM算法:系出同源,一脉相承
Markdown公式、特殊字符、上下标、求和/积分、分式/根式、字体
相关文章:
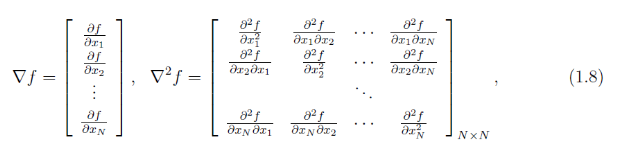
牛顿法、梯度下降法与拟牛顿法
牛顿法、梯度下降法与拟牛顿法 0 引言1 关于泰勒展开式1.1 原理1.2 例子 2 牛顿法2.1 x 为一维2.2 x 为多维 3 梯度下降法4 拟牛顿法4.1 拟牛顿条件4.2 DFP 算法4.3 BFGS 算法4.4 L-BFGS 算法 0 引言 机器学习中在求解非线性优化问题时,常用的是梯度下降法和拟牛顿…...
带你浅谈下Quartz的简单使用
Scheduler 每次执行,都会根据JobDetail创建一个新的Job实例,这样就可以规避并发访问的问题(jobDetail的实例也是新的) Quzrtz 定时任务默认都是并发执行,不会等待上一次任务执行完毕,只要间隔时间到就会执…...

C++ cout格式化输出
称为“流操纵算子”),使用更加方便。 C cout成员方法格式化输出 《C输入流和输出流》一节中,已经针对 cout 讲解了一些常用成员方法的用法。除此之外,ostream 类中还包含一些可实现格式化输出的成员方法,这些成员方法…...

查询练习:复制表的数据作为条件查询
查询某课程成绩比该课程平均成绩低的 score 表。 -- 查询平均分 SELECT c_no, AVG(degree) FROM score GROUP BY c_no; -------------------- | c_no | AVG(degree) | -------------------- | 3-105 | 87.6667 | | 3-245 | 76.3333 | | 6-166 | 81.6667 | ------…...
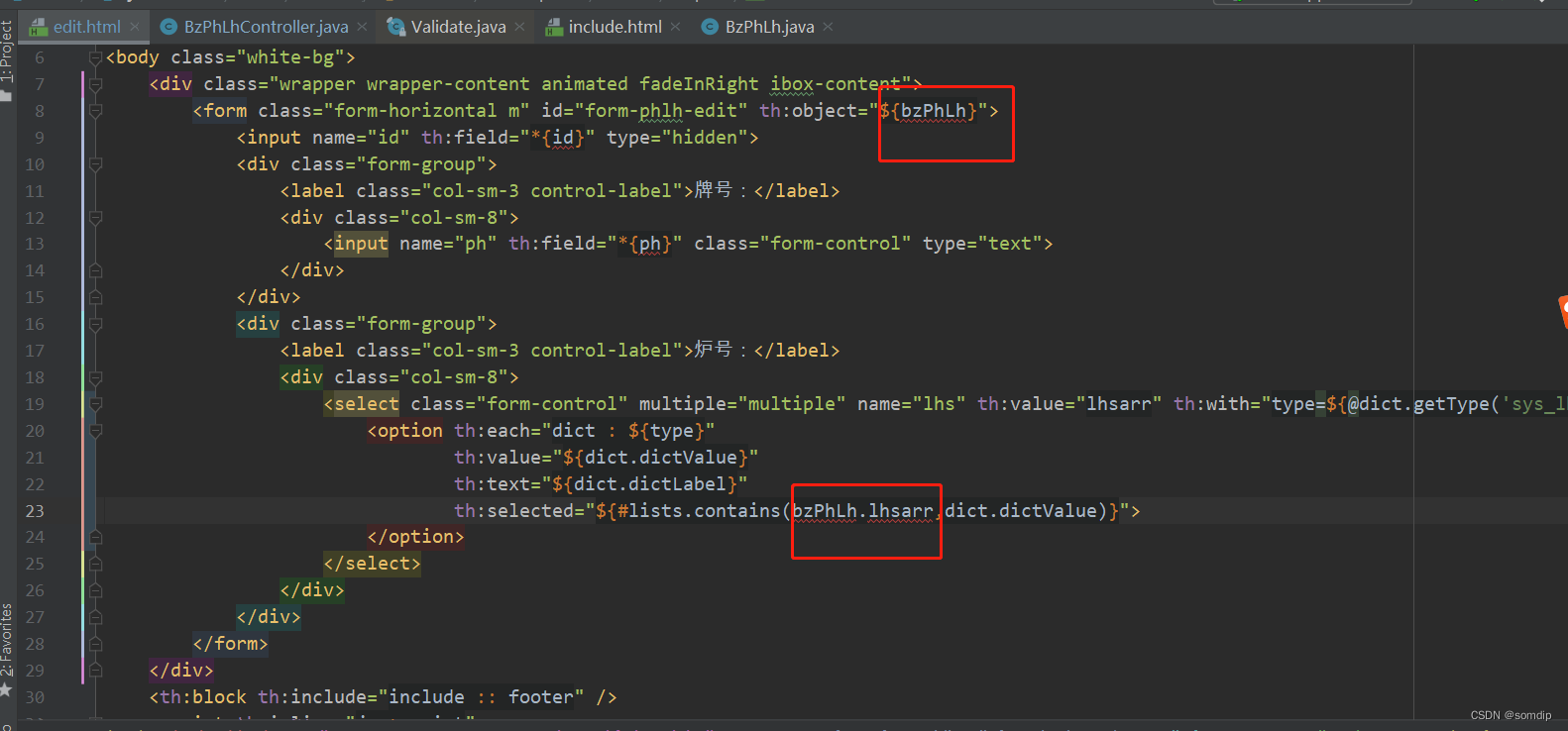
Thymeleaf select回显并选中多个
语法: selected"selected" 或 selectedtrue ${#strings.indexOf(name,frag)} 或者 ${#lists.contains(list, element)} 或者 ${#strings.contains(name,ez)} 或者 ${#strings.containsIgnoreCase(name,ez)} 都可以实现。 多选示例 : &…...

【Go 基础】变量
1. 变量 Go 语言是静态类型语言,由于编译时,编译器会检查变量的类型,所以要求所有的变量都要有明确的类型 。 变量在使用前,需要先声明。声明类型,就约定了你这个变量只能赋该类型的值。 1.1 变量声明 格式&#x…...

国网B接口语音对讲和广播技术探究及与GB28181差别
接口描述 在谈国网B接口的语音广播和语音对讲的时候,大家会觉得,国网B接口是不是和GB28181大同小异?实际上确实信令有差别,但是因为要GB28181设备接入测的对接,再次做国网B接口就简单多了。 语音对讲和广播包括信令接…...

非计算机专业如何转行成为程序员?我用亲身经历教你用这三种方法
哈喽大家好啊!我想分享一下,非计算机专业的学生如何转行成为程序员。首先,我先介绍一下我的情况。我是18年毕业的,大学学的专业是土木工程,与计算机一点关系都没有。但是在大学时,我对程序员比较感兴趣。本…...

2023年最新网络安全渗透工程师面试题汇总!不看亏大了!
技术面试问题 CTF 说一个印象深刻的CTF的题目 Padding Oracle->CBC->密码学(RSA/AES/DSA/SM) CRC32 反序列化漏洞 sql二次注入 第一次进行数据库插入数据的时候,仅仅只是使用了 addslashes 或者是借助get_magic_quotes_gpc 对其中的特殊字符进行了转义&…...
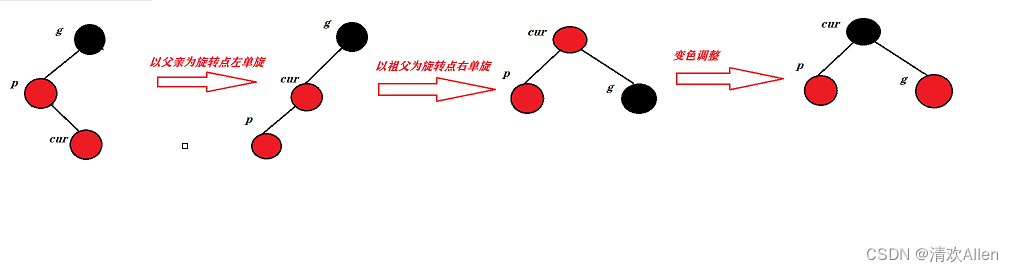
红黑树(C++实现)
文章目录 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的查找红黑树的验证检测是否满足二叉搜索树检测是否满足红黑树的性质 红黑树与AVL树的比较包含上述功能的红黑树代码 红黑树的概念 红黑树,是一棵二叉搜索树,但在每一个结点上增加一个存储位表示结点的颜色…...

leetcode尊享面试 100 题 - 1427. 字符串的左右移
尊享面试 100 题是Leetcode会员专享题单 1427. 字符串的左右移 力扣题目链接 给定一个包含小写英文字母的字符串 s 以及一个矩阵 shift,其中 shift[i] [direction, amount]: direction 可以为 0 (表示左移)或 1 (表…...

进来看看!跨境电商要这样选品才能做出爆款
今天要聊的是跨境电商怎么做系列的第三期,前面两期聊完平台和货源之后,就到了选品。目前网络上很多都是告诉你不同平台要怎么选品。龙哥这期有些不同,不会和你说哪个品类最受欢迎,而是告诉你你要怎么去选择出适合自己、适合市场的…...
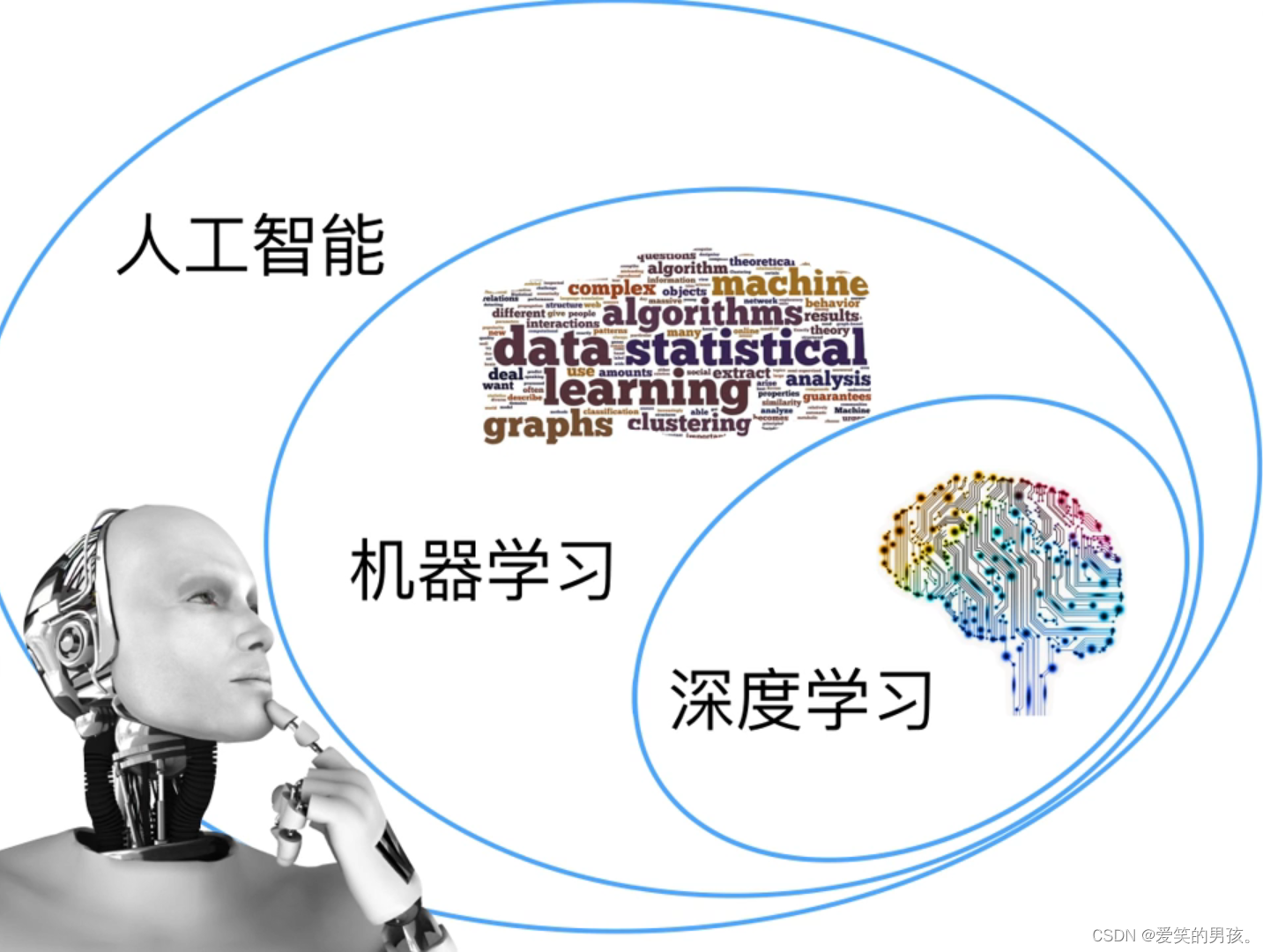
什么是深度学习?
目录 简介 深度学习的由来 深度学习未来的趋势 总结 简介 深度学习是在20世纪80年代被提出来的,主要是由加拿大的计算机科学家Geoffrey Hinton、Yoshua Bengio、Yann LeCun等人发起的。Geoffrey Hinton等人在经过多年的研究和实践之后,…...

追梦之旅【数据结构篇】——看看小白试如何利用C语言“痛”撕堆排序
追梦之旅【数据结构篇】——看看小白试如何利用C语言“痛”撕堆排序 ~😎 前言🙌堆的应用 —— 堆排序算法:堆排序算法源代码分享运行结果测试截图: 总结撒花💞 😎博客昵称:博客小梦 ὠ…...
python版pytorch模型转openvino及调用
一、openvino安装 参看官方文档https://www.intel.com/content/www/us/en/developer/tools/openvino-toolkit/download.html 安装命令是根据上面的选择生成。这里安装了pytorch和onnx依赖。 二、pytorch模型转opnvino模型推理 import os import time import cv2 import nu…...

TensorFlow 机器学习秘籍第二版:9~11
原文:TensorFlow Machine Learning Cookbook 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何…...

【苏州数字力量】面经 base上海
文章目录 【苏州数字力量】面经 base上海Java基础面1.说一下常见的数据类型、大小、以及他们的封装类2.重载和重写的区别3.谈谈Java的引用方式4.String有些什么方法5.String、StringBuffer、StringBuilder的区别是什么6.谈一下static有哪些用法7.谈一下常见的访问修饰符有哪些&…...

FVM链的Themis Pro(0x,f4) 5日IDO超百万美元,或让Filecoin逆风翻盘
交易一直是DeFi乃至web3领域最经久不衰的话题,也因此催生了众多优秀的去中心化协议,如Uniswap和Curve。这些协议逐渐成为了整个系统的基石。 在永续合约方面,DYDX的出现将WEB2时代的订单簿带回了web3。其链下交易的设计,仿佛回到了…...
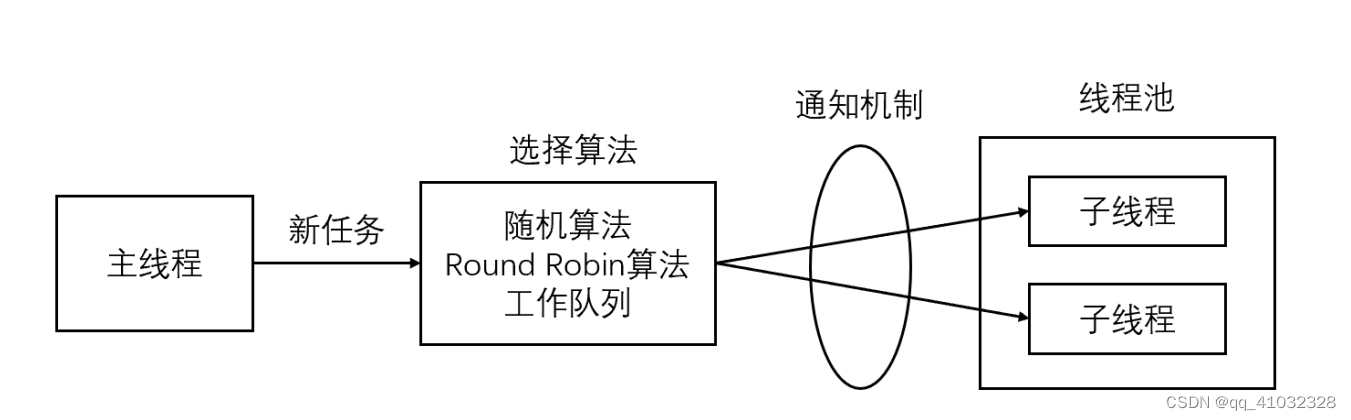
webserve简介
目录 I/O分类I/O模型阻塞blocking非阻塞 non-blocking(NIO)IO复用信号驱动异步 webServerHTTP简介概述工作原理HTTP请求头格式HTTP请求方法HTTP状态码 服务器编程基本框架两种高效的事件处理模式Reactor模式Proactor模拟 Proactor 模式 线程池 I/O分类 …...
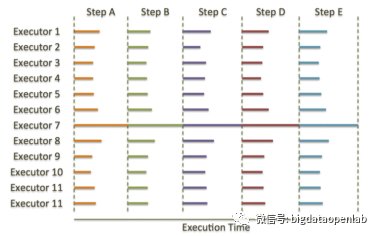
分析型数据库:MPP 数据库的概念、技术架构与未来发展方向
随着企业数据量的增多,为了配合企业的业务分析、商业智能等应用场景,从而驱动数据化的商业决策,分析型数据库诞生了。由于数据分析一般涉及的数据量大,计算复杂,分析型数据库一般都是采用大规模并行计算或者分布式计算…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
