红黑树(C++实现)
文章目录
- 红黑树的概念
- 红黑树的性质
- 红黑树结点的定义
- 红黑树的插入
- 红黑树的查找
- 红黑树的验证
- 检测是否满足二叉搜索树
- 检测是否满足红黑树的性质
- 红黑树与AVL树的比较
- 包含上述功能的红黑树代码
红黑树的概念
红黑树,是一棵二叉搜索树,但在每一个结点上增加一个存储位表示结点的颜色,可以是Red或Black.通过任何一条从根到叶子上的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的.
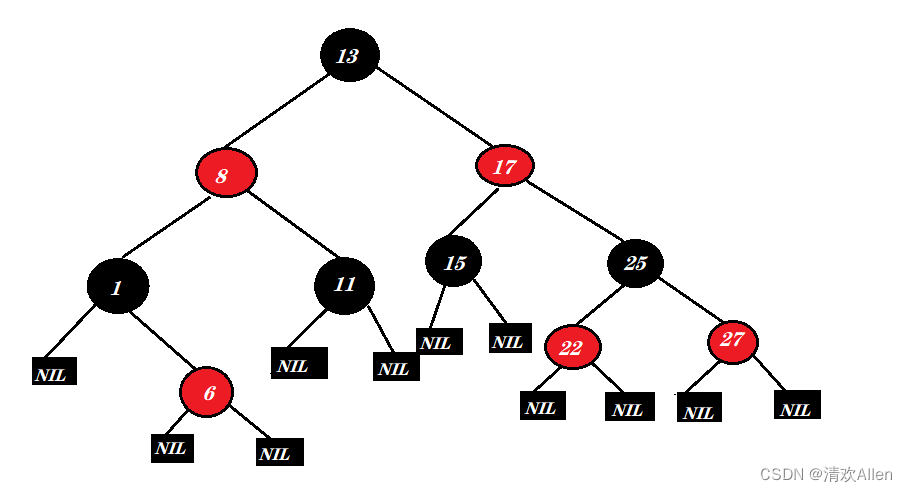
红黑树的性质
1: 每个结点不是红色就是黑色.
2: 根节点是黑色的
3: 如果一个结点是红色的,则它的两个孩子结点是黑色的.
4: 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点.
5: 每个叶子结点都是黑色的(此处的叶子结点指的是NIL结点,也就是空结点).
依据以上5个性质,怎么保证红黑树的最长路径不会超过最短路径的两倍呢?
我们可以假设,在红黑树中,如果每个路径的黑色结点都是N个,那么在棵红黑树中最短路径长度就为N.(假设N为2)
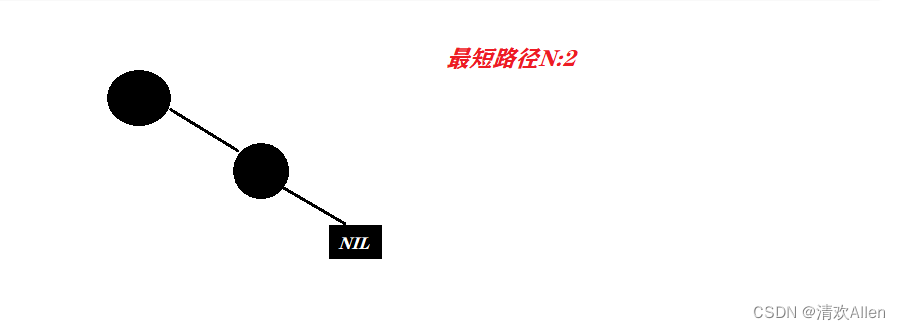
根据性质3,性质4,那么最长路径也是N个黑色结点,并且由多对一黑一红结点组成,此时,最长路径的长度即为2N.(假设N为2)
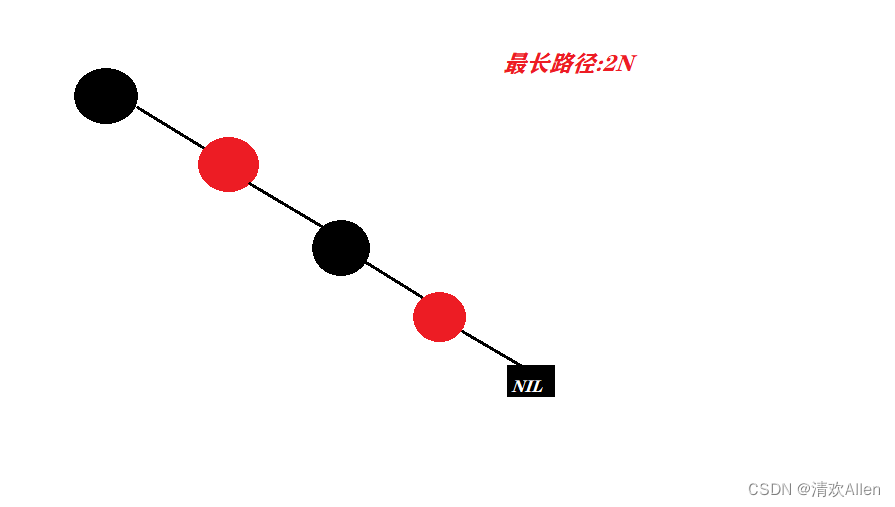
所以,在红黑树中,最长路径长度等于最短路径长度的两倍,不可能超过最短路径的两倍.
红黑树结点的定义
我们实现的是KV模型结构的红黑树,由于红黑树需要旋转,我们将红黑树的结点定义为三叉链结构,并且添加一个新成员_col,代表结点的颜色,方便后续的变色平衡.
enum Colour
{RED,BLACK
};
template <class K, class V>
struct RBTreeNode //三叉链
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv; //存储的键值对Colour _col; //标志着红黑树的颜色.RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED) //将结点默认定义为红色.{}
};
思考: 在结点的定义中,为什么要将结点的默认颜色给成红色的?
1:如果我们在红黑树的一条路径中插入一个黑色结点,由于性质4,那么便会影响红黑树的其它路径,为了保持平衡,其他路径都可能需要变色+旋转.
2: 如果我们在红黑树的一条路径中插入一个红色结点,由于性质三,最多只会影响插入的那一条路径,我们只需要对该条路径变色+旋转来保持平衡就行.
所以,为了将红黑树的插入影响降到最低,我们选择将红黑树的结点默认定义为红色.
红黑树的插入
红黑树的插入主要分为三个步骤:
1: 找到红黑树的插入位置.
2: 将插入结点插入到寻找的插入位置.
3: 检测新结点插入后,红黑树的性质是否发生改变,并对其进行相应调整.
其中步骤1和步骤2和AVL树的插入相同,但是步骤三相较AVL树的插入有了较大改变.
那么查看红黑树性质的依据是什么?
在红黑树的插入中:
1: 如果插入结点的父亲结点是黑色的,那么该次插入并没有破坏红黑树的性质,则该次插入并不需要调整平衡.
2: 如果插入结点的父亲结点是红色的,那么根据红黑树的性质2,父亲结点一定有grandfater结点且为黑色结点.
3: 如果插入结点为父亲结点是红色的,那么根据插入结点的叔叔结点(即parent的兄弟结点)的情况,进行调整平衡.
此时有三种情况:
情况一: 插入结点的叔叔存在,并且叔叔结点的颜色为红色.
为了防止出现连续的红结点,我们需要将父亲结点变黑,又为了保持每条路径的黑色结点的个数相同,我们将祖父结点变红,将叔叔结点变黑.因此,我们既可以解决连续出现红色结点的问题,又可以保持每条路径的黑色结点相同.
变色调整抽象图如下:
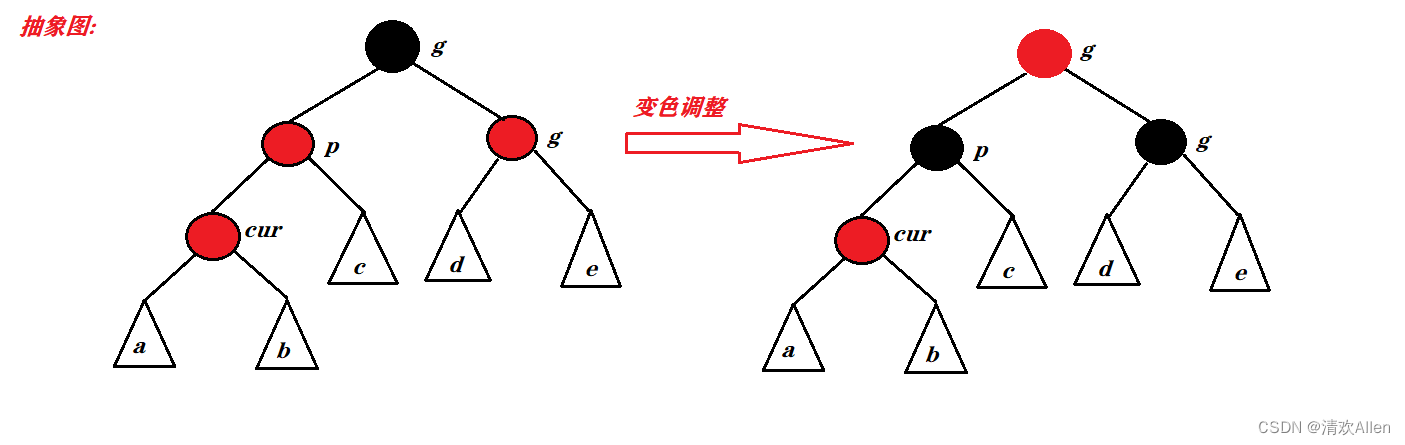
注意:
1:如果此时的祖父结点即为整棵树的根结点,:那么为了保持根节点为黑结点的性质,我们需要将祖父变为黑色结点后,退出循环.
2: 如果此时的祖父结点为整棵树的子树,那么我们需要将cur指向祖父节点,parent指向cur的父亲结点后,根据叔叔的情况继续平衡.
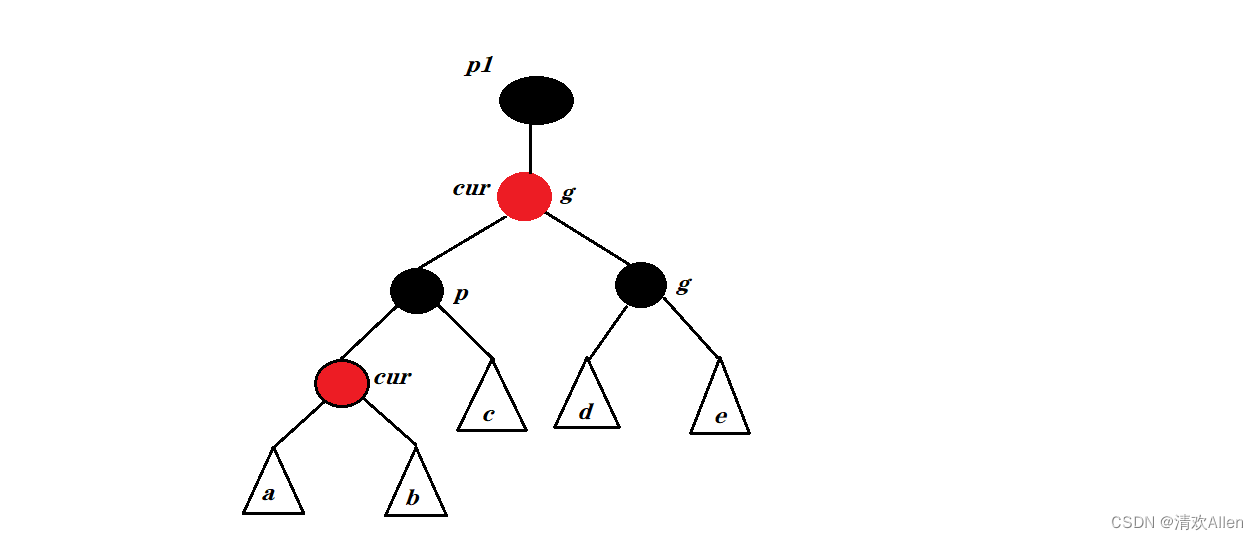
3: 当叔叔存在且为红色结点时,cur是parent的左孩子还是右孩不影响变色平衡.
情况二: 插入结点的叔叔存在,并且叔叔结点的颜色为黑色.
插入前:
1: d,e 可以是空树或者是一个红色结点.
2: c可以是根是黑节点的子树,为例图右侧四种子树的任意一种.
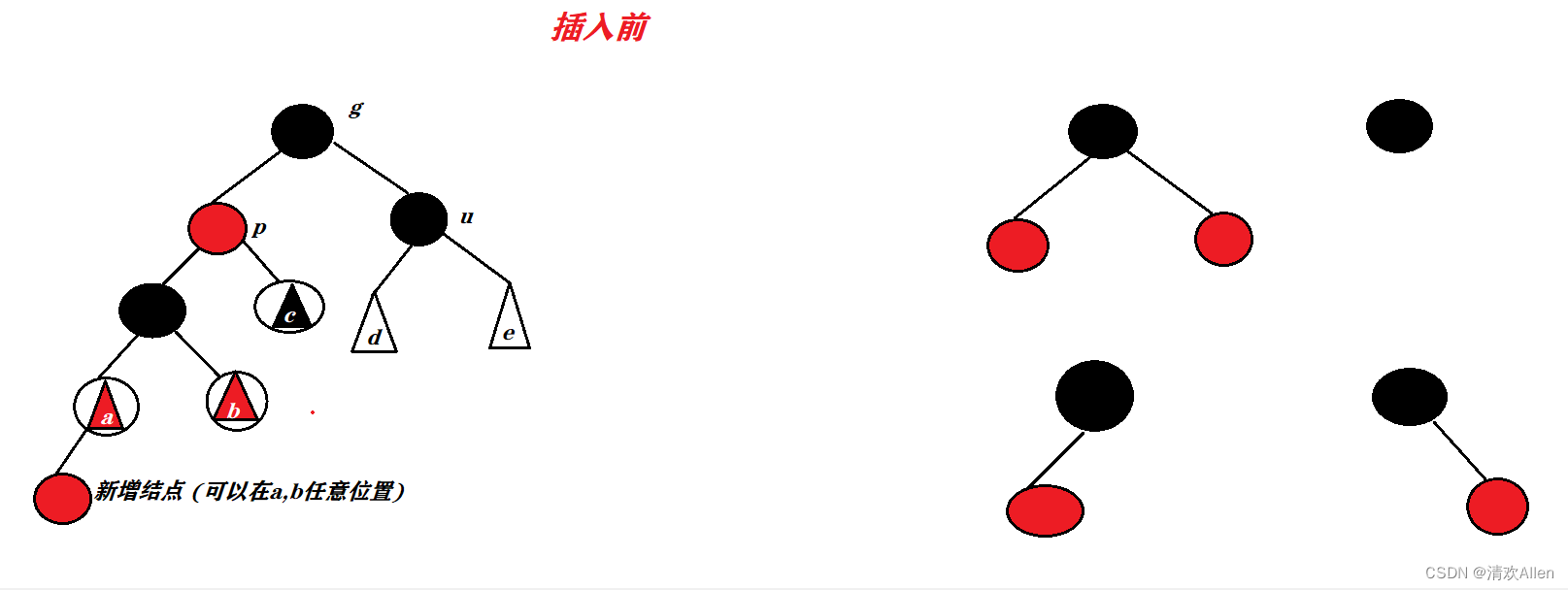
插入后
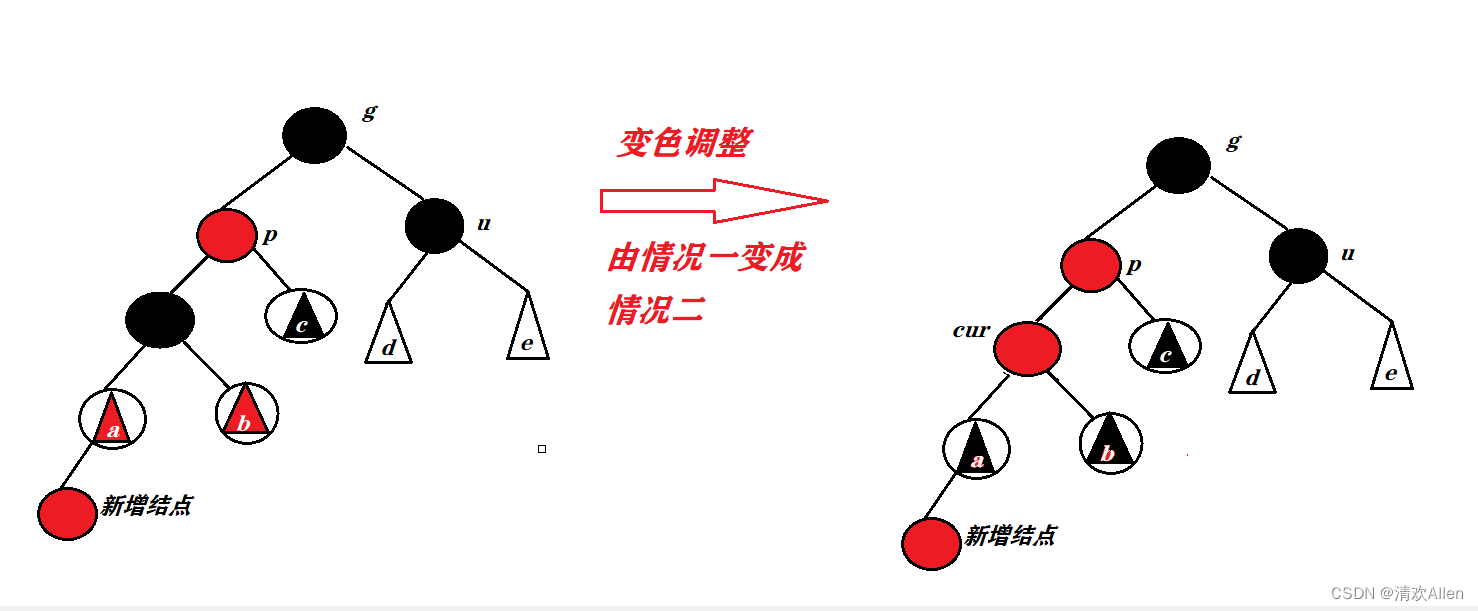
由插入前后例图可见,情况二的出现主要由情况一插入时变色调整导致的.
当叔叔存在且为黑色结点时,此时需要旋转+变色调整平衡,但是旋转时打又有两种情况:
(1):如果祖先,父亲,儿子三个结点的路径为一条直线,首先,于祖父所在的红黑树来说,左子树的路径的长度已经大于最短路径的两倍了,此时需要以祖先为旋转点右单旋(降左子树的高度),为了保持红黑树的每条路径的黑色结点个数相等,我们需要将父亲结点调整为黑色结点,再将祖父结点调整为红色结点.
旋转+变色抽象图如下:
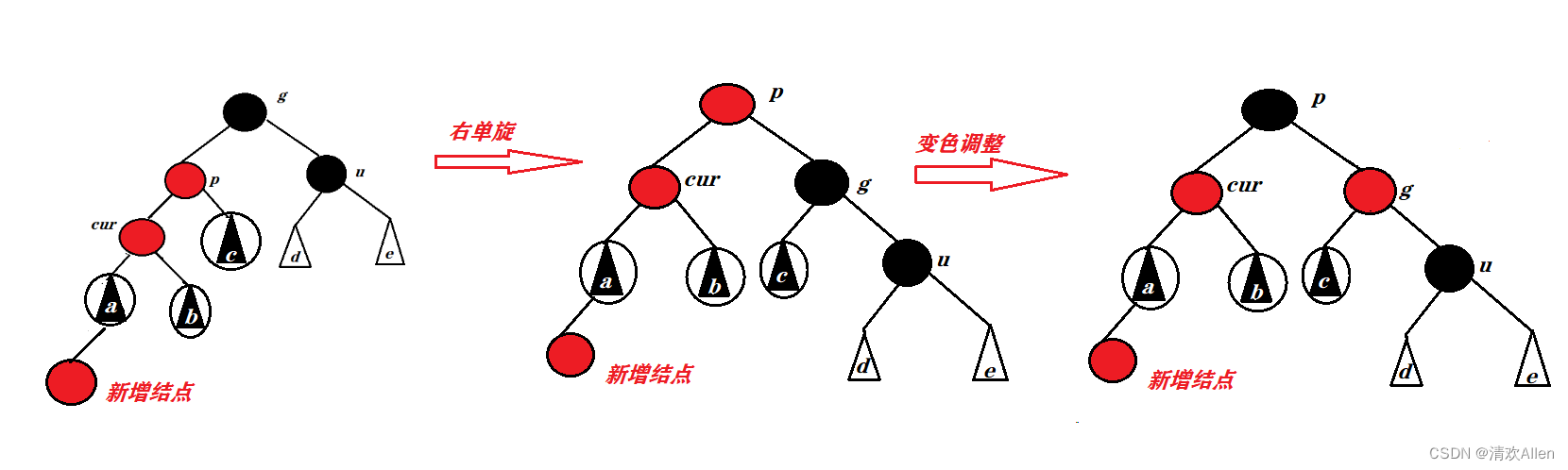
(2)如果祖先,父亲,儿子三个结点的路径为一条折线,我们需要先以父亲为旋转点左单旋,然后再以祖父为旋转点右单旋,将祖父调整为红色结点,将孩子结点调整为黑色结点,进而保持了每条路径的的的黑色结点个数相同.
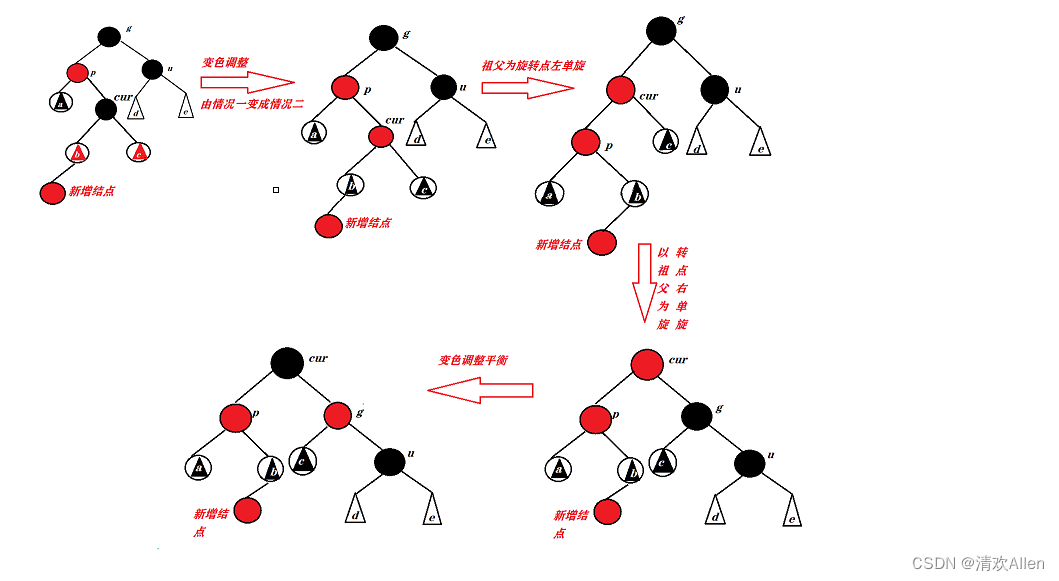
注意:
颜色调整后,无论这棵树是整棵树还是子树,根节点是黑色的,且已经保持平衡,所以无需继续往上处理.
情况三: 插入结点的叔叔不存在,且a/b/c/d/e为空树
情况三又分为两种情况:
1:如果祖父,父亲,孩子结点组成的路径为一条直线:
首先祖父结点左子树的路径长度大于最短路径的两倍,此时需要以祖父右单旋降左子树高度,然后将父亲结点调整为黑色结点,将祖父结点调整为红色结点.
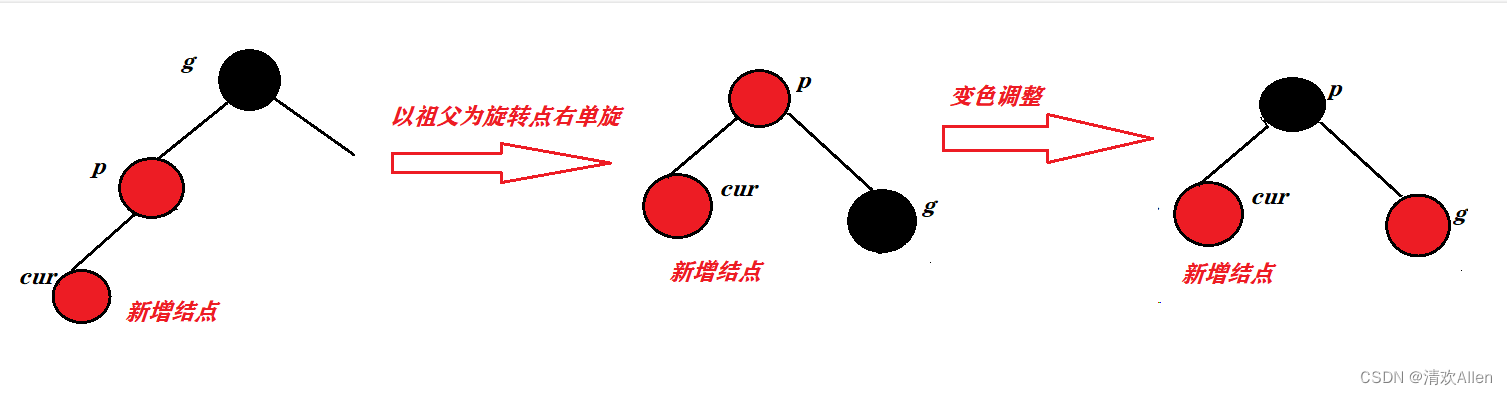
2:如果祖父,父亲,孩子结点组成的路径为一条折线.
同理,首先,我们先以父亲结点为旋转点左单旋,然后再以祖父为旋转点右单旋,最后,再将孩子结点调整为黑色结点,祖父结点调整为红色结点.
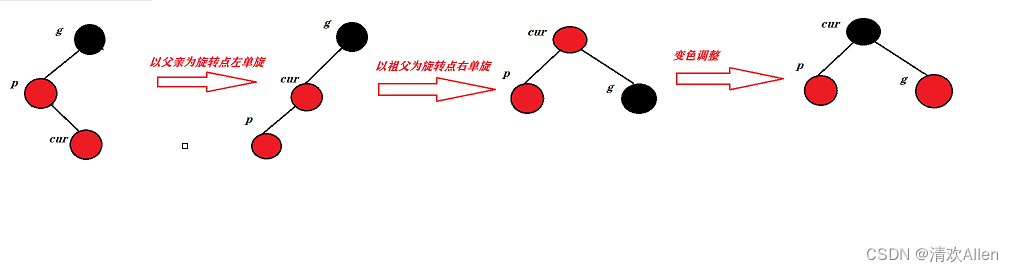
红黑树的插入函数代码如下:
bool Insert(const pair<K, V>& kv) //插入函数{if (_root == nullptr) //如果为空树,直接插入结点就可以了.{_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur) //寻找插入位置{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv); //找到插入位置并插入.cur->_col = RED; //新插入结点的颜色为红色.if (parent->_kv.first < kv.first) //与父亲结点建立联系{parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while ( parent && parent->_col == RED ) //达到平衡条件,需要调整平衡.{Node* grandfater = parent->_parent;assert(grandfater);assert(grandfater->_col == BLACK);if ( parent == grandfater->_left ) //判断父亲在祖父的位置,如果父亲在祖父的左边{Node* uncle = grandfater->_right;if ( uncle && uncle->_col == RED ) //将父亲和叔叔的颜色变黑,祖父的颜色变红.{ parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater; //继续向上寻找parent = grandfater->_parent;}else //uncle不存在或者存在且为黑{ // g // p//curif (cur == parent->_left) //如果祖父,父亲,孩子路径为一条直线{RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}// g// p// curelse //如果祖父,父亲,孩子路径为一条折线.{ RotateL(parent);RotateR(grandfater);cur->_col = BLACK; grandfater->_col = RED; }//走到这里大该子树的根已经变成黑色结点了,不用再往上循环了.break;}}else //如果父亲在祖父的右边.{// g// u p // c//Node* uncle = grandfater->_left;if (uncle && uncle->_col == RED) //如果叔叔存在且为红色结点.{parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater; //继续向上变色循环.parent = grandfater->_parent;}else //如果父亲不存在,或者存在且为黑色结点.{// g // p// c if (parent->_right == cur) //如果父亲,祖父,孩子路径为一条直线{RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}// g// p// celse //如果父亲,祖父,孩子路径为一条折线{RotateR(parent);RotateL(grandfater);grandfater->_col = RED;cur->_col = BLACK;}break;}}}_root->_col = BLACK; //走到这说明这棵树没有的祖先没有parent,或者有parent但是父亲是黑色的,不需要处理.return true;}void RotateL(Node* parent) //左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent) //右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
红黑树的查找
查找步骤:
1: 如果所给值大于cur所指结点first,那么从左边遍历查找.
2: 如果所给值大于cur所指结点first,那么从右边遍历查找.
3: 找到了就返回.
4: 但退出循环还没找到,就说明找不到了,返回nullptr.
Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key ) //如果key大于当前结点的first{cur = cur->_right;}else if (cur->_kv.first > key) //如果key小于当前结点的first{cur = cur->_left;}else //寻找到了{return cur;}}return nullptr;}
红黑树的验证
检测是否满足二叉搜索树
红黑树也是一棵接近平衡的二叉搜索树,因此,我们可以通过中序遍历,进而查看是否满足二叉搜索树的性质.
void InOrder() //中序遍历{_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":"<< root->_kv.second << endl;_InOrder(root->_right);}
检测是否满足红黑树的性质
我们可以检测红黑树的四个性质进而推出红黑树的最长路径长度不超过最短路径的两倍.最后可以判断是否平衡.
1: 性质一可以通过代码的颜色枚举中证明.
2: 性质二和性质三可以在递归中进行判断.
3: 性质四,我们可以设计一个基准值,先求出第一条路径的黑色结点个数为基准值,然后当其他的路径走完时,将其他路径黑色结点个数与该基准值分别比较.
bool PreCheck(Node* root,int& benchMark, int blackNum) //判断性质四{if (root == nullptr){if (benchMark == 0){benchMark = blackNum;;return true;}if (blackNum != benchMark){cout << "某条黑色结点数量不相等." << endl;return false;}else {return true;}}if ( root->_col == RED && root->_parent->_col == RED )//判断性质三{return false;}if (root->_col == BLACK){++blackNum;}return PreCheck(root->_left,benchMark ,blackNum) && PreCheck(root->_right,benchMark, blackNum);}bool _IsBalance( Node* root ) //要从红黑树的四个性质分别判断{if (root == nullptr ){return true;}if (root->_col == RED) //判断性质一{cout << "根节点不是黑色结点" << endl;return false;}int benchMark = 0; //黑色结点数量基准值.return PreCheck(root,benchMark,0);}
红黑树与AVL树的比较
1:红黑树和AVL树都是高效的平衡二叉树,增删查改的时间复杂度都为O(log2N),红黑树不追求绝对平衡,只需要保证最长路径的长度不超过最短路径的两倍.
2:在插入或者删除中,红黑树降低了旋转的次数,所以需要多次增删操作中,红黑树的性能比AVL树的性能更加高效,而且红黑树的实现相对AVL树来说比较简单,在实践中使用红黑树更多.
包含上述功能的红黑树代码
#include <iostream>
#include <assert.h>
#include <map>
using namespace std;
enum Colour
{RED,BLACK
};
template <class K, class V>
struct RBTreeNode //三叉链
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv; //存储的键值对Colour _col; //标志着红黑树的颜色.RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv){}
};
template <class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key ) //如果key大于当前结点的first{cur = cur->_right;}else if (cur->_kv.first > key) //如果key小于当前结点的first{cur = cur->_left;}else //寻找到了{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);}bool Insert(const pair<K, V>& kv) //插入函数{if (_root == nullptr) //如果为空树,直接插入结点就可以了.{_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur) //寻找插入位置{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv); //找到插入位置并插入.cur->_col = RED; //新插入结点的颜色为红色.if (parent->_kv.first < kv.first) //与父亲结点建立联系{parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while ( parent && parent->_col == RED ) //达到平衡条件,需要调整平衡.{Node* grandfater = parent->_parent;assert(grandfater);assert(grandfater->_col == BLACK);if ( parent == grandfater->_left ) //判断父亲在祖父的位置,如果父亲在祖父的左边{Node* uncle = grandfater->_right;if ( uncle && uncle->_col == RED ) //将父亲和叔叔的颜色变黑,祖父的颜色变红.{ parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater; //继续向上寻找parent = grandfater->_parent;}else //uncle不存在或者存在且为黑{ // g // p//curif (cur == parent->_left) //如果祖父,父亲,孩子路径为一条直线{RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}// g// p// curelse //如果祖父,父亲,孩子路径为一条折线.{ RotateL(parent);RotateR(grandfater);cur->_col = BLACK; grandfater->_col = RED; }//走到这里大该子树的根已经变成黑色结点了,不用再往上循环了.break;}}else //如果父亲在祖父的右边.{// g// u p // c//Node* uncle = grandfater->_left;if (uncle && uncle->_col == RED) //如果叔叔存在且为红色结点.{parent->_col = uncle->_col = BLACK;grandfater->_col = RED;cur = grandfater; //继续向上变色循环.parent = grandfater->_parent;}else //如果父亲不存在,或者存在且为黑色结点.{// g // p// c if (parent->_right == cur) //如果父亲,祖父,孩子路径为一条直线{RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}// g// p// celse //如果父亲,祖父,孩子路径为一条折线{RotateR(parent);RotateL(grandfater);grandfater->_col = RED;cur->_col = BLACK;}break;}}}_root->_col = BLACK; //走到这说明这棵树没有的祖先没有parent,或者有parent但是父亲是黑色的,不需要处理.return true;}bool IsBalance(){return _IsBalance(_root);}
private:bool PreCheck(Node* root,int& benchMark, int blackNum) //判断性质四{if (root == nullptr){if (benchMark == 0){benchMark = blackNum;;return true;}if (blackNum != benchMark){cout << "某条黑色结点数量不相等." << endl;return false;}else {return true;}}if ( root->_col == RED && root->_parent->_col == RED )//判断性质三{return false;}if (root->_col == BLACK){++blackNum;}return PreCheck(root->_left,benchMark ,blackNum) && PreCheck(root->_right,benchMark, blackNum);}bool _IsBalance( Node* root ) //要从红黑树的四个性质分别判断{if (root == nullptr ){return true;}if (root->_col == RED) //判断性质一{cout << "根节点不是黑色结点" << endl;return false;}int benchMark = 0; //黑色结点数量基准值.return PreCheck(root,benchMark,0);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":"<< root->_kv.second << endl;_InOrder(root->_right);}void RotateL(Node* parent) //左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent) //右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}Node* _root = nullptr;};
//测试1
void TestRBTree1()
{int a[] = { 16,3,7,11,9,26,18,14,15,0,1 };RBTree<int, int> t1;for (auto e : a){
t1.Insert(make_pair(e, e));}t1.InOrder();cout << "IsBalance:" << t1.IsBalance() << endl;
}//测试2
//随机数测试,使用10000个随机数测试
void TestRBTree2()
{size_t N = 10000;srand(time(0));RBTree<int, int> t1;for (size_t i = 0; i < N; ++i){int x = rand(); //x接收产生的随机数.t1.Insert(make_pair(x, i)); //在树中插入随机数.}t1.InOrder();cout << t1.Find(1)->_kv.first << endl;cout << "IsBanlance:" << t1.IsBalance() << endl;
}
相关文章:

红黑树(C++实现)
文章目录 红黑树的概念红黑树的性质红黑树结点的定义红黑树的插入红黑树的查找红黑树的验证检测是否满足二叉搜索树检测是否满足红黑树的性质 红黑树与AVL树的比较包含上述功能的红黑树代码 红黑树的概念 红黑树,是一棵二叉搜索树,但在每一个结点上增加一个存储位表示结点的颜色…...

leetcode尊享面试 100 题 - 1427. 字符串的左右移
尊享面试 100 题是Leetcode会员专享题单 1427. 字符串的左右移 力扣题目链接 给定一个包含小写英文字母的字符串 s 以及一个矩阵 shift,其中 shift[i] [direction, amount]: direction 可以为 0 (表示左移)或 1 (表…...

进来看看!跨境电商要这样选品才能做出爆款
今天要聊的是跨境电商怎么做系列的第三期,前面两期聊完平台和货源之后,就到了选品。目前网络上很多都是告诉你不同平台要怎么选品。龙哥这期有些不同,不会和你说哪个品类最受欢迎,而是告诉你你要怎么去选择出适合自己、适合市场的…...
什么是深度学习?
目录 简介 深度学习的由来 深度学习未来的趋势 总结 简介 深度学习是在20世纪80年代被提出来的,主要是由加拿大的计算机科学家Geoffrey Hinton、Yoshua Bengio、Yann LeCun等人发起的。Geoffrey Hinton等人在经过多年的研究和实践之后,…...

追梦之旅【数据结构篇】——看看小白试如何利用C语言“痛”撕堆排序
追梦之旅【数据结构篇】——看看小白试如何利用C语言“痛”撕堆排序 ~😎 前言🙌堆的应用 —— 堆排序算法:堆排序算法源代码分享运行结果测试截图: 总结撒花💞 😎博客昵称:博客小梦 ὠ…...
python版pytorch模型转openvino及调用
一、openvino安装 参看官方文档https://www.intel.com/content/www/us/en/developer/tools/openvino-toolkit/download.html 安装命令是根据上面的选择生成。这里安装了pytorch和onnx依赖。 二、pytorch模型转opnvino模型推理 import os import time import cv2 import nu…...

TensorFlow 机器学习秘籍第二版:9~11
原文:TensorFlow Machine Learning Cookbook 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何…...

【苏州数字力量】面经 base上海
文章目录 【苏州数字力量】面经 base上海Java基础面1.说一下常见的数据类型、大小、以及他们的封装类2.重载和重写的区别3.谈谈Java的引用方式4.String有些什么方法5.String、StringBuffer、StringBuilder的区别是什么6.谈一下static有哪些用法7.谈一下常见的访问修饰符有哪些&…...

FVM链的Themis Pro(0x,f4) 5日IDO超百万美元,或让Filecoin逆风翻盘
交易一直是DeFi乃至web3领域最经久不衰的话题,也因此催生了众多优秀的去中心化协议,如Uniswap和Curve。这些协议逐渐成为了整个系统的基石。 在永续合约方面,DYDX的出现将WEB2时代的订单簿带回了web3。其链下交易的设计,仿佛回到了…...
webserve简介
目录 I/O分类I/O模型阻塞blocking非阻塞 non-blocking(NIO)IO复用信号驱动异步 webServerHTTP简介概述工作原理HTTP请求头格式HTTP请求方法HTTP状态码 服务器编程基本框架两种高效的事件处理模式Reactor模式Proactor模拟 Proactor 模式 线程池 I/O分类 …...
分析型数据库:MPP 数据库的概念、技术架构与未来发展方向
随着企业数据量的增多,为了配合企业的业务分析、商业智能等应用场景,从而驱动数据化的商业决策,分析型数据库诞生了。由于数据分析一般涉及的数据量大,计算复杂,分析型数据库一般都是采用大规模并行计算或者分布式计算…...
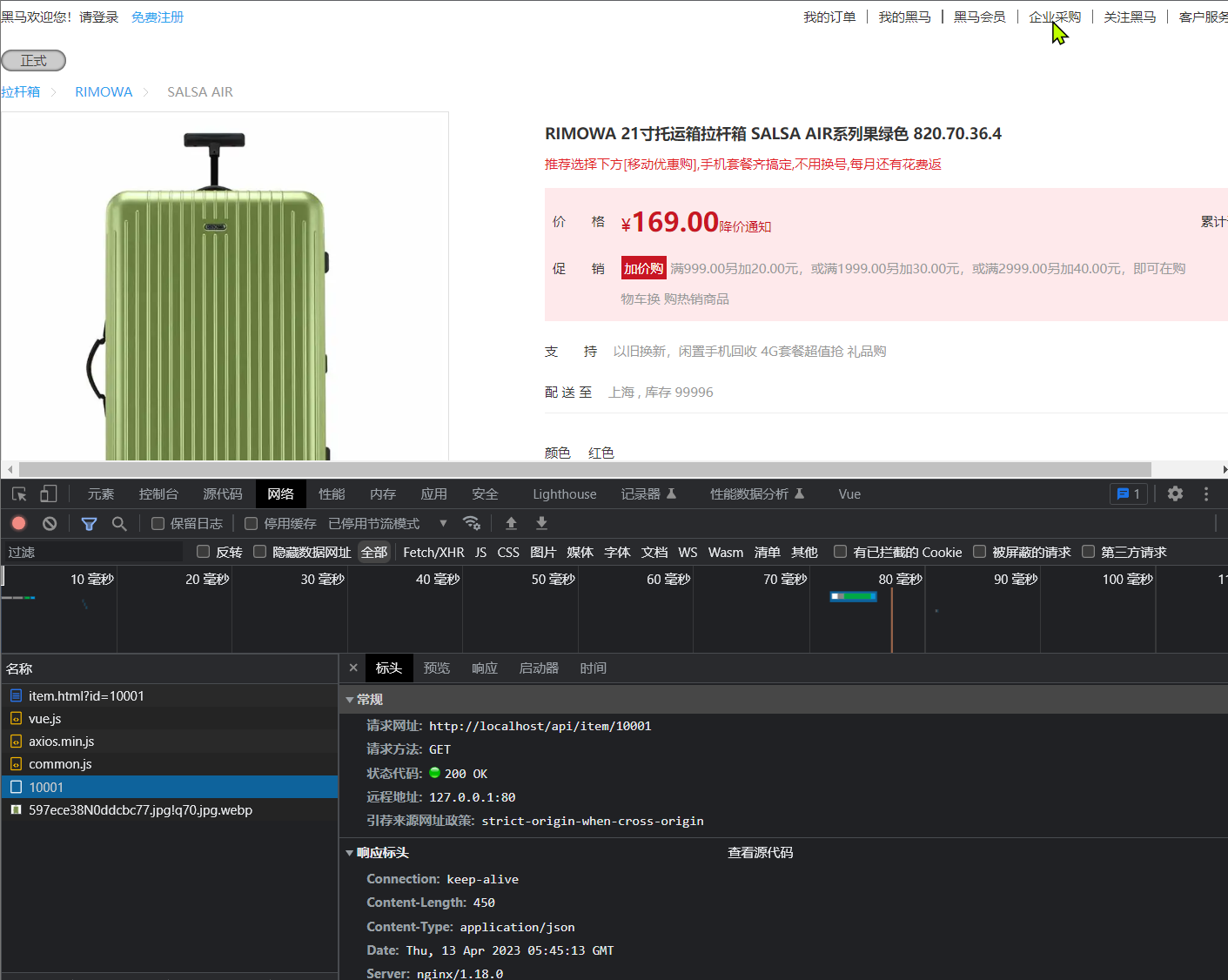
微服务高级篇学习【4】之多级缓存
文章目录 前言一 多级缓存二 JVM进程缓存2.1 案例导入2.1.1 使用docker安装mysql2.1.2 修改配置2.1.3 导入项目工程2.1.4 导入商品查询页面2.1.5 反向代理 2.2 初识Caffeine2.3 实现JVM进程缓存 三 Lua脚本入门3.1 安装Lua3.2 Lua语法学习 四 实现多级缓存4.1 OpenResty简介4.2…...

知乎版ChatGPT「知海图AI」加入国产大模型乱斗,称效果与GPT-4持平
“2023知乎发现大会”上,知乎创始人、董事长兼CEO周源和知乎合作人、CTO李大海共同宣布了知乎与面壁智能联合发布“知海图AI”中文大模型。 周源据介绍,知乎与面壁智能达成深度合作,共同开发中文大模型产品并推进应用落地。目前,知…...

邮件发送配置
QQ邮箱发送和接收配置: POP3/SMTP协议 接收邮件服务器:pop.exmail.qq.com ,使用SSL,端口号995 发送邮件服务器:smtp.exmail.qq.com ,使用SSL,端口号465 海外用户可使用以下服务器 接收邮件服务器…...
【Open CASCADE -生成MFC和QT事例方式】
源代码目录 adm目录:包含编译OCCT的相关工程; adm/cmake目录:包含使用CMake构建OCCT的相关处理脚本; adm/msvc目录:包含window平台 Visual C 2010, 2012, 2013, 2015, 2017 and 2019等版本的32/64平台solutinon文件; data目录: 包…...
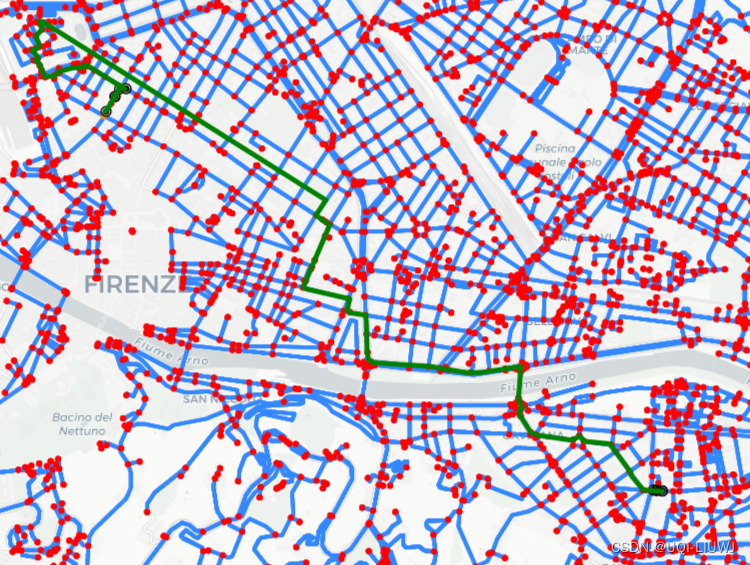
python 笔记:PyTrack(将GPS数据和OpenStreetMap数据进行整合)【官网例子解读】
论文笔记:PyTrack: A Map-Matching-Based Python Toolbox for Vehicle Trajectory Reconstruction_UQI-LIUWJ的博客-CSDN博客4 0 包的安装 官网的两种方式我都试过,装是能装成功,但是python import PyTrack包的时候还是显示找不到Pytrack …...
)
苦中作乐 ---竞赛刷题31-40(15-20)
(一)目录 L1-032 Left-pad L1-033 出生年 L1-034 点赞 L1-035 情人节 L1-039 古风排版 (二)题目 L1-032 Left-pad 根据新浪微博上的消息,有一位开发者不满NPM(Node Package Manager)的做法…...

100种思维模型之人类误判心理思维模型-49
“我们老得太快,聪明得太迟”——查理芒格。 2005年,81岁的查理芒格认为81岁的他能够比10年前做得更好。他决定对1992年2月2日、1994年10月6日和1995年4月24日的三次演讲稿进行修改,于是就有了这个人类误判心理思维模型——25条人类误判心理学…...
【从零开始学Skynet】实战篇《球球大作战》(十三):场景代码设计(下)
1、主循环 《球球大作战》是一款服务端运算的游戏,一般会使用主循环程序结构,让服务端处理战斗逻辑。如下图所示,图中的 balls 和 foods代表服务端的状态,在循环中执行“ 食物生成”“位置更新”和“碰撞检 测” 等功能࿰…...
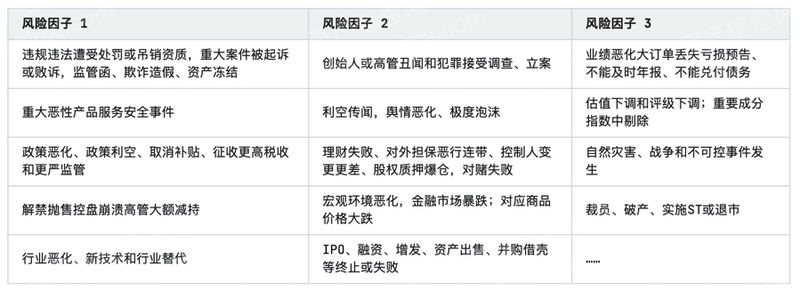
2023年虚拟数字人行业研究报告
第一章 行业概况 虚拟数字人指存在于非物理世界中,由计算机图形学、图形渲染、动作捕捉、深度学习、语音合成等计算机手段创造及使用,并具有多种人类特征(外貌特征、人类表演能力、人类交互能力等)的综合产物。虚拟人可分为服务型…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
