哈希表题目:在系统中查找重复文件
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 解法
- 思路和算法
- 代码
- 复杂度分析
- 进阶问题答案
- 后记
题目
标题和出处
标题:在系统中查找重复文件
出处:609. 在系统中查找重复文件
难度
6 级
题目描述
要求
给定一个目录信息列表 paths \texttt{paths} paths,包括目录路径和该目录中的所有包含内容的文件,返回文件系统中的所有重复文件组的路径。你可以按任意顺序返回结果。
一组重复的文件至少包括两个具有完全相同内容的文件。
输入列表中的单个目录信息字符串的格式如下:
- "root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content)" \texttt{"root/d1/d2/.../dm f1.txt(f1\_content) f2.txt(f2\_content) ... fn.txt(fn\_content)"} "root/d1/d2/.../dm f1.txt(f1_content) f2.txt(f2_content) ... fn.txt(fn_content)"
这意味着在目录 root/d1/d2/.../dm \texttt{root/d1/d2/.../dm} root/d1/d2/.../dm 下有 n \texttt{n} n 个文件 (f1.txt, f2.txt ... fn.txt) \texttt{(f1.txt, f2.txt ... fn.txt)} (f1.txt, f2.txt ... fn.txt),内容分别是 (f1_content, f2_content ... fn_content) \texttt{(f1\_content, f2\_content ... fn\_content)} (f1_content, f2_content ... fn_content)。注意: n ≥ 1 \texttt{n} \ge \texttt{1} n≥1 且 m ≥ 0 \texttt{m} \ge \texttt{0} m≥0。如果 m = 0 \texttt{m} = \texttt{0} m=0,则表示该目录是根目录。
输出是重复文件路径组的列表。对于每个组,它包含具有相同内容的文件的所有文件路径。文件路径是具有下列格式的字符串:
- "directory_path/file_name.txt" \texttt{"directory\_path/file\_name.txt"} "directory_path/file_name.txt"
示例
示例 1:
输入: paths = ["root/a 1.txt(abcd) 2.txt(efgh)", "root/c 3.txt(abcd)", "root/c/d 4.txt(efgh)", "root 4.txt(efgh)"] \texttt{paths = ["root/a 1.txt(abcd) 2.txt(efgh)", "root/c 3.txt(abcd)", "root/c/d 4.txt(efgh)", "root 4.txt(efgh)"]} paths = ["root/a 1.txt(abcd) 2.txt(efgh)", "root/c 3.txt(abcd)", "root/c/d 4.txt(efgh)", "root 4.txt(efgh)"]
输出: [["root/a/2.txt","root/c/d/4.txt","root/4.txt"],["root/a/1.txt","root/c/3.txt"]] \texttt{[["root/a/2.txt","root/c/d/4.txt","root/4.txt"],["root/a/1.txt","root/c/3.txt"]]} [["root/a/2.txt","root/c/d/4.txt","root/4.txt"],["root/a/1.txt","root/c/3.txt"]]
示例 2:
输入: paths = ["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"] \texttt{paths = ["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"]} paths = ["root/a 1.txt(abcd) 2.txt(efgh)","root/c 3.txt(abcd)","root/c/d 4.txt(efgh)"]
输出: [["root/a/2.txt","root/c/d/4.txt"],["root/a/1.txt","root/c/3.txt"]] \texttt{[["root/a/2.txt","root/c/d/4.txt"],["root/a/1.txt","root/c/3.txt"]]} [["root/a/2.txt","root/c/d/4.txt"],["root/a/1.txt","root/c/3.txt"]]
数据范围
- 1 ≤ paths.length ≤ 2 × 10 4 \texttt{1} \le \texttt{paths.length} \le \texttt{2} \times \texttt{10}^\texttt{4} 1≤paths.length≤2×104
- 1 ≤ paths[i].length ≤ 3000 \texttt{1} \le \texttt{paths[i].length} \le \texttt{3000} 1≤paths[i].length≤3000
- 1 ≤ sum(paths[i].length) ≤ 5 × 10 5 \texttt{1} \le \texttt{sum(paths[i].length)} \le \texttt{5} \times \texttt{10}^\texttt{5} 1≤sum(paths[i].length)≤5×105
- paths[i] \texttt{paths[i]} paths[i] 由英语字母、数字、 ‘/’ \texttt{`/'} ‘/’、 ‘.’ \texttt{`.'} ‘.’、 ‘(’ \texttt{`('} ‘(’、 ‘)’ \texttt{`)'} ‘)’ 和 ‘ ’ \texttt{` '} ‘ ’ 组成
- 你可以假设在同一目录中没有任何文件或目录共享相同的名称
- 你可以假设每个给定的目录信息代表一个唯一的目录,目录路径和文件信息用一个空格分隔
进阶
- 假设给你一个真正的文件系统,你将如何搜索文件?深度优先搜索还是广度优先搜索?
- 如果文件内容非常大(GB 级别),你将如何修改你的解决方案?
- 如果每次只能读取 1 KB 的文件,你将如何修改你的解决方案?
- 修改后的解决方案的时间复杂度是多少?其中最消耗时间的部分和最消耗内存的部分是什么?如何优化?
- 如何确保你发现的重复文件不是误报?
解法
思路和算法
给定的数组 paths \textit{paths} paths 中的每个元素表示一个目录的路径以及该目录中的所有文件的文件名和文件内容。如果一个元素包含用空格分隔的 m m m 项,则可以将该元素使用空格作为分隔符创建长度为 m m m 的数组,数组中的第 0 0 0 项为目录路径,其余 m − 1 m - 1 m−1 项分别为该目录中的每个文件的文件信息,包括文件名和文件内容,可以根据数组中的每个元素得到每个文件的绝对路径和文件内容。
为了找到重复文件,需要找到每种文件内容对应的文件列表,并判断文件列表中的文件个数,如果文件个数大于 1 1 1 则该文件列表为一组重复文件。可以使用哈希表记录每种文件内容对应的文件列表。
由于文件系统中的任意两个目录的路径都不同,任意两个文件的绝对路径都不同,因此不需要对目录的路径和文件的绝对路径做排重操作,使用列表表示每种文件内容的文件列表即可。
对于数组 paths \textit{paths} paths 中的每个元素,首先将该元素使用空格作为分隔符创建文件数组,然后对文件数组中的除了第 0 0 0 项以外的每一项得到文件的绝对路径和文件内容,在哈希表中将文件的绝对路径添加到文件内容的文件列表中。
遍历结束数组 paths \textit{paths} paths 之后,遍历哈希表,对于哈希表中的每种文件内容,如果对应的文件列表中的文件个数大于 1 1 1,则将该文件列表添加到结果中。
代码
class Solution {public List<List<String>> findDuplicate(String[] paths) {Map<String, List<String>> map = new HashMap<String, List<String>>();for (String path : paths) {String[] array = path.split(" ");StringBuffer directoryBuffer = new StringBuffer(array[0]);if (directoryBuffer.charAt(directoryBuffer.length() - 1) != '/') {directoryBuffer.append('/');}String directory = directoryBuffer.toString();int length = array.length;for (int i = 1; i < length; i++) {String fileNameContent = array[i];int fileNameContentLength = fileNameContent.length();int leftParenthesisIndex = -1;StringBuffer fileNameBuffer = new StringBuffer();for (int j = 0; j < fileNameContentLength && leftParenthesisIndex < 0; j++) {char c = fileNameContent.charAt(j);if (c == '(') {leftParenthesisIndex = j;} else {fileNameBuffer.append(c);}}String fileName = fileNameBuffer.toString();String content = fileNameContent.substring(leftParenthesisIndex + 1, fileNameContentLength - 1);String completeFileName = directory + fileName;map.putIfAbsent(content, new ArrayList<String>());map.get(content).add(completeFileName);}}List<List<String>> duplicates = new ArrayList<List<String>>();Set<Map.Entry<String, List<String>>> entries = map.entrySet();for (Map.Entry<String, List<String>> entry : entries) {String content = entry.getKey();List<String> files = entry.getValue();if (files.size() > 1) {duplicates.add(files);}}return duplicates;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是文件系统中的文件总数。遍历文件系统中的全部文件并将每种文件内容和对应的文件列表存入哈希表,需要 O ( n ) O(n) O(n) 的时间,遍历哈希表得到结果也需要 O ( n ) O(n) O(n) 的时间。这里将字符串操作的时间视为 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是文件系统中的文件总数。空间复杂度主要取决于哈希表,哈希表中需要存储每种文件内容对应的文件列表,空间是 O ( n ) O(n) O(n)。这里将字符串占用的空间视为 O ( 1 ) O(1) O(1)。
进阶问题答案
-
假设给你一个真正的文件系统,你将如何搜索文件?深度优先搜索还是广度优先搜索?
深度优先搜索和广度优先搜索的时间复杂度相同,因此应该根据空间复杂度决定使用哪种搜索方法。
如果文件系统树结构的深度是 d d d,平均分支数是 f f f(即树结构中的每个目录结点平均有 f f f 个子结点),则深度优先搜索的空间复杂度是 O ( d ) O(d) O(d),广度优先搜索的空间复杂度是 O ( f d ) O(f^d) O(fd)。大多数情况下, O ( d ) O(d) O(d) 优于 O ( f d ) O(f^d) O(fd),因此大多数情况下应该使用深度优先搜索。 -
如果文件内容非常大(GB 级别),你将如何修改你的解决方案?
如果文件内容非常大,则不能一次性存储文件的完整内容,因此需要将文件内容分块存储,并存储元数据,元数据包括文件名、文件大小、各分块的偏移量、各分块的哈希值等。
其中,一个分块的哈希值等于该分块的内容使用特定哈希函数计算得到的结果,每个文件的所有分块的哈希值计算都使用同一个哈希函数。
如果两个文件的内容相同,则这两个文件的大小一定也相同。因此,比较两个文件的内容是否相同时,首先比较两个文件的大小是否相同,如果大小不同则内容一定不同,如果大小相同再依次比较每个分块的哈希值是否相同,只要有一个分块的哈希值不同,则两个文件的内容不同,只有当每个分块的哈希值都相同时,才能认为两个文件的内容可能相同。使用哈希值进行比较虽然可以降低内存空间(只需要将哈希值存入内存,不需要将文件内容直接存入内存),但是可能存在误报的情况,问题 5 将提供解决方案。 -
如果每次只能读取 1 KB 的文件,你将如何修改你的解决方案?
每次只能读取 1 KB 的文件,则每个分块的大小最多为 1 KB,因此使用问题 2 的解决方案,将每个分块的大小设为 1 KB。
-
修改后的解决方案的时间复杂度是多少?其中最消耗时间的部分和最消耗内存的部分是什么?如何优化?
如果文件系统中的文件个数是 n n n,每个文件的平均大小是 k k k,则时间复杂度是 O ( k n 2 ) O(kn^2) O(kn2)。对于每个文件需要 O ( k ) O(k) O(k) 的时间计算元数据,其中计算每个分块哈希值的时间复杂度最高,共需要 O ( k n ) O(kn) O(kn) 的时间计算元数据。每两个文件之间都需要比较,比较次数是 n ( n − 1 ) 2 \dfrac{n(n - 1)}{2} 2n(n−1),每次比较首先比较文件大小,然后比较每个分块的哈希值,因此最坏情况下每次比较的时间复杂度是 O ( k ) O(k) O(k),总时间复杂度是 O ( k n 2 ) O(kn^2) O(kn2)。
最消耗时间和内存的部分是哈希值的计算和存储。
由于文件个数 n n n 和比较次数 n ( n − 1 ) 2 \dfrac{n(n - 1)}{2} 2n(n−1) 无法减少,因此可以优化的方面只有哈希值的计算。在条件允许的情况下,将每个分块的大小增加,即可减少分块个数。 -
如何确保你发现的重复文件不是误报?
误报的情况为两个文件的内容不同但是两个文件中的每个分块的哈希值对应相同。为了避免误报,当两个文件中的每个分块的哈希值都对应相同时,需要比较两个文件的内容,只有当内容相同时才能认为是重复文件。
后记
这道题的进阶问题涉及到搜索,搜索是在树和图中常用的算法。由于文件系统是一个树的结构,因此搜索文件需要使用到搜索算法。常见的搜索算法有深度优先搜索和广度优先搜索。
深度优先搜索的做法是从起点出发,沿着一条路搜索到底,然后依次回退到之前遍历的每一个位置,寻找其他尚未遍历的路并继续搜索,直到搜索完所有的位置。
广度优先搜索的做法是从起点出发,按照距离从近到远的顺序依次搜索每个位置。
关于树的搜索,将在树结构部分具体讲解。关于其他场景下的搜索,将在搜索算法部分具体讲解。
相关文章:

哈希表题目:在系统中查找重复文件
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 解法思路和算法代码复杂度分析 进阶问题答案后记 题目 标题和出处 标题:在系统中查找重复文件 出处:609. 在系统中查找重复文件 难度 6 级 题目描述 要求 给定一个目录信息列表 paths…...
机器人感知与控制关键技术及其智能制造应用
源自:自动化学报 作者:王耀南 江一鸣 姜娇 张辉 谭浩然 彭伟星 吴昊天 曾凯 摘 要 智能机器人在服务国家重大需求, 引领国民经济发展和保障国防安全中起到重要作用, 被誉为“制造业皇冠顶端的明珠”. 随着新一轮工业革命的到来, 世界主要工业国…...

精通线程池,看这一篇就够了
一:什么是线程池 当我们运用多线程技术处理任务时,需要不断通过new的方式创建线程,这样频繁创建和销毁线程,会造成cpu消耗过多。那么有没有什么办法避免频繁创建线程呢? 当然有,和我们以前学习过多连接池技术类似&…...

解决图片、视频地址加密问题
const getImgUrl async () > {const imgUrl 远程链接地址const response await fetch(imgUrl)//取出blob二进制const blob await response.blob()//url转为类似blob:http://localhost:9587/cf3265b9-75eb-4722-8e11-5048dec2564d//赋值给需要展示的地方const url URL.c…...

GPT引领学习之旅:一篇让程序员轻松掌握Elasticsearch的攻略
一、引言 随着大数据技术的飞速发展,程序员们面临着越来越多的挑战。Elasticsearch作为一款流行的开源搜索和分析引擎,已成为许多项目的重要组成部分。那么如何高效地学习并掌握Elasticsearch呢?在这篇文章中,我们将探讨如何运用…...
)
23种设计模式-仲裁者模式(Android应用场景介绍)
仲裁者模式是一种行为设计模式,它允许将对象间的通信集中到一个中介对象中,以减少对象之间的耦合度。本文将通过Java语言实现仲裁者模式,并介绍如何在安卓开发中使用该模式。 实现仲裁者模式 我们将使用一个简单的例子来说明仲裁者模式的实…...
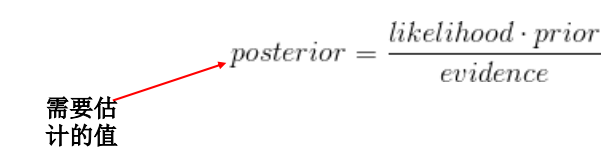
【数据统计】— 极大似然估计 MLE、最大后验估计 MAP、贝叶斯估计
【数据统计】— 极大似然估计 MLE、最大后验估计 MAP、贝叶斯估计 极大似然估计、最大后验概率估计(MAP),贝叶斯估计极大似然估计(Maximum Likelihood Estimate,MLE)MLE目标例子: 扔硬币极大似然估计—高斯分布的参数 矩估计 vs LSE vs MLE贝叶斯公式&am…...

Zookeeper学习笔记
Zookeeper入门 Zookeeper 是一个开源的分布式的,为分布式框架提供协调服务的Apache 项目。 Zookeeper工作机制 Zookeeper从设计模式角度来理解:是一个基于观察者模式设计的分布式服务管理框架,它负责存储和管理大家都关心的数据,…...
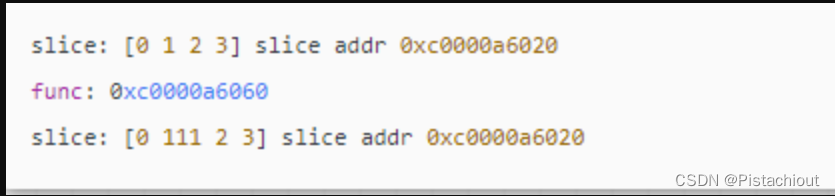
go语言切片做函数参数传递+append()函数扩容
go语言切片函数参数传递append()函数扩容 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 二叉树递归go代码: var ans [][]int func pathSum(root *TreeNode, targetSum int) ( [][…...
2023.04.16 学习周报
文章目录 摘要文献阅读1.题目2.摘要3.简介4.Dual-Stage Attention-Based RNN4.1 问题定义4.2 模型4.2.1 Encoder with input attention4.2.2 Decoder with temporal attention4.2.3 Training procedure 5.实验5.1 数据集5.2 参数设置和评价指标5.3 实验结果 6.结论 MDS降维算法…...
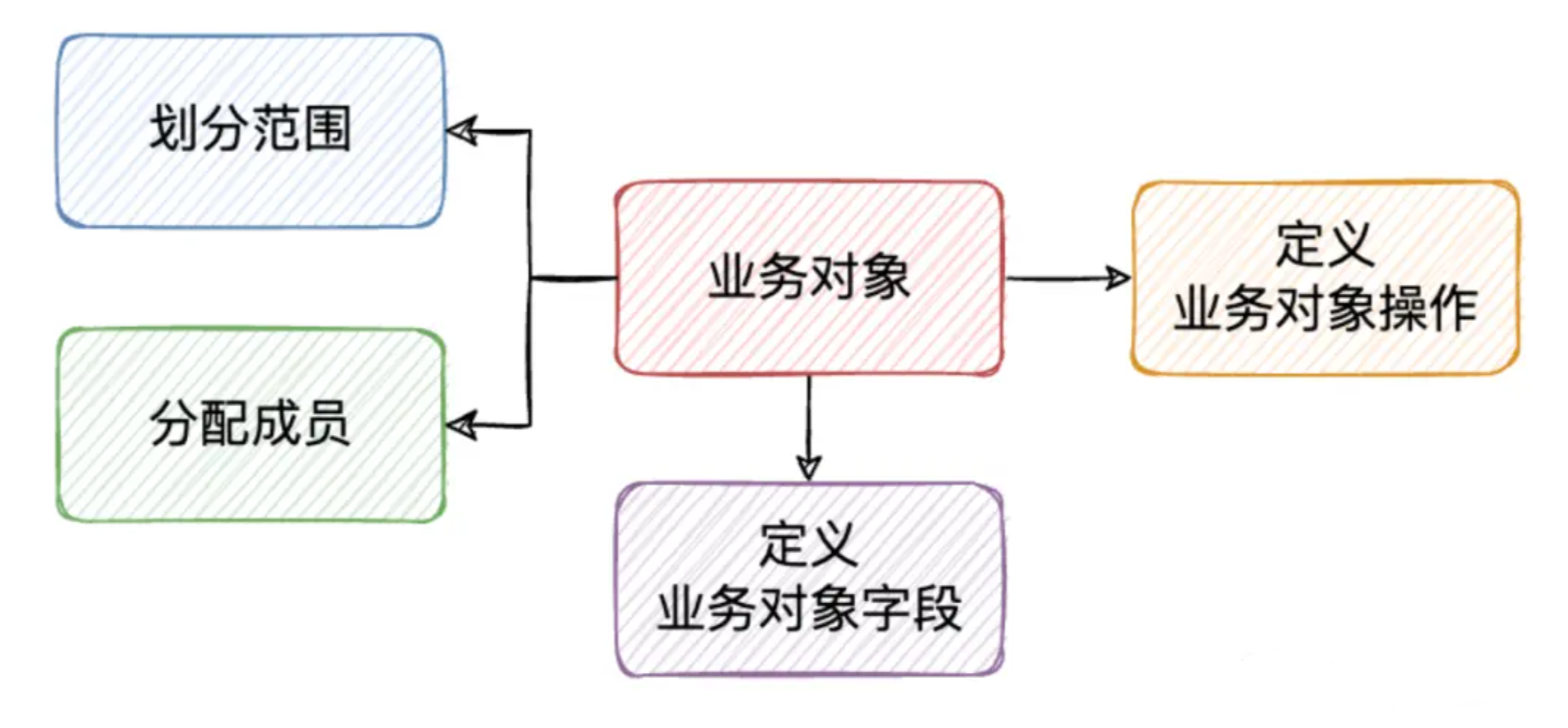
【面试】如何设计SaaS产品的数据权限?
文章目录 前言数据权限是什么?设计原则整体方案RBAC模型怎么控制数据权限?1. 数据范围权限控制2. 业务对象操作权限控制3. 业务对象字段权限控制 总结 前言 一套系统的权限可以分为两类,数据权限和功能权限,今天我们从以下几个点…...

ansible管理变量
ansible变量简介 变量用于存储值,便于重复使用,可以简化项目的创建和维护。 变量命令规则 ansible变量的名称必须以字母开头,平且只能包含字母、数字和下划线,不允许有其他特殊字符。 变量范围 全局范围:从命令行…...

一种轻量级日志采集解决方案
前言 目前各大公司生产部署很多都是采用的集群微服务的部署方式,如果让日志散落在各个主机上,查询起来会非常的困难,所以目前我了解到的都是采用的日志中心来统一收集管控日志,日志中心的实现方案大多基于ELK(即Elasticsearch、L…...
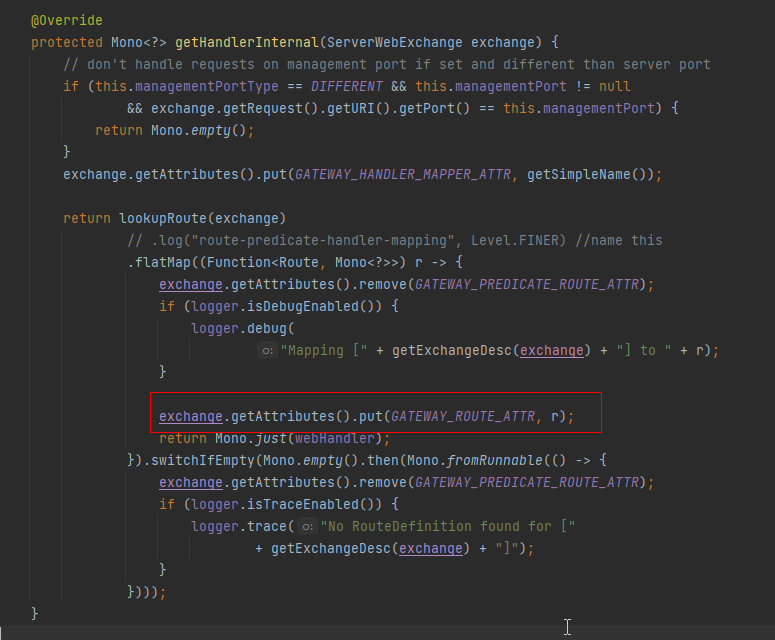
【源码】Spring Cloud Gateway 是在哪里匹配路由的?
我们知道,经过网关的业务请求会被路由到后端真实的业务服务上去,假如我们使用的是Spring Cloud Gateway,那么你知道Spring Cloud Gateway是在哪一步去匹配路由的吗? 源码之下无秘密,让我们一起从源码中寻找答案。 入…...

BAT批处理基本命令
什么是 BAT 批处理脚本语言? BAT 批处理脚本语言是 Windows 系统自带的一种脚本语言,主要用于批量处理文件、目录、注册表、系统设置等任务。使用 BAT 批处理脚本语言可以节省大量手动操作的时间和精力。 如何编写 BAT 批处理脚本? 使用记事本…...
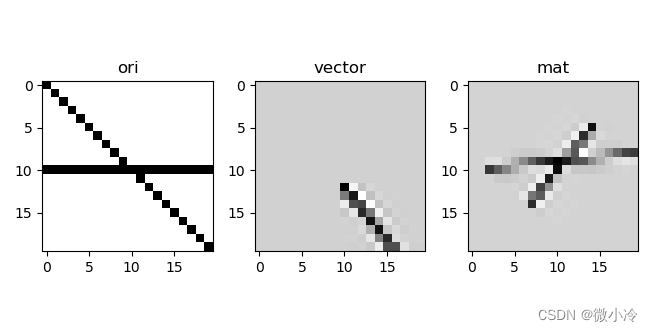
Python数组仿射变换
文章目录 仿射变换坐标变换的逻辑scipy实现 仿射变换 前面提到的平移、旋转以及缩放,都可以通过一个变换矩阵来实现,以二维空间中的变换矩阵为例,记点的坐标向量为 ( x , y , 1 ) (x,y,1) (x,y,1),则平移矩阵可表示为 [ 1 0 T x …...

“==“和equals方法究竟有什么区别?
操作符专门用来比较两个变量的值是否相等,也就是用于比较变量所对应的内存中所存储的数值是否相同,要比较两个基本类型的数据或两个引用变量是否相等,只能用操作符。 如果一个变量指向的数据是对象类型的,那么,这时候…...
蓝桥杯15单片机--超声波模块
目录 一、超声波工作原理 二、超声波电路图 三、程序设计 1-设计思路 2-具体实现 四、程序源码 一、超声波工作原理 超声波时间差测距原理超声波发射器向某一方向发射超声波,在发射时刻的同时开始计时,超声波在空气中传播,途中碰到障碍…...

【学习笔记】ARC159
D - LIS 2 因为没有让你求方案数,所以还是比较好做的。 如果每一个连续段都退化成一个点,那么答案就是直接求 L I S LIS LIS。 否则,假设我们选了一些连续段把它们拼起来形成答案,显然我们有 r i 1 ≥ l i r_{i1}\ge l_i ri1…...

2023/4/16总结
图的存储 链式前向星 链式前向星和邻接表很相似,只是存储方式变成了数组。 链式前向星一般要用到一个结构体数组和一个一维数组,结构体数组edges中包括三个变量。结构体数组的大小一般由边的大小决定。 edges数组中的to代表的是某条边的终点v。w代表的是这条边的…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
