【题解】P4055 [JSOI2009] 游戏
link
题目大意
题目说得比较清楚。
题解
前置知识:二分图最大匹配、基础博弈论。
每个点只能走一次的四联通点阵,可以想到二分图匹配。
将其套路地奇偶分点,相邻两点连边(显然不能为 #)。
先求一个最大匹配。
如果是完美匹配,那么 LOSE. 因为小 AA 将棋子放到任意一点,小 YY 都能走匹配边走到另一部,小 AA 就只能走非匹配边。每一点都有一条匹配边,最后小 YY 会走最后一条匹配边,这时所有点都走完了。小 AA 败。
现在考虑 WIN. 首先,若小 AA 选择非匹配点,那么小 AA 必胜。显然,非匹配点的邻接点都为匹配点,否则就不是最大匹配。当小 AA 放下棋子后,小 YY 走到匹配点上。然后,小 AA 走匹配边。则小 YY 此时只能走非匹配边。以非匹配点为开始的一条路径,路径的结尾只能是匹配点。这个点只有一条边连出,为匹配边。最后,小 AA 会通过这条匹配边走到结尾,小 AA 胜。
所以小 AA 选非匹配点时胜利。
再来观察下图。黑点为匹配点,边权为 1 1 1 的是匹配边。

我们还有另一种方案:
 那么点 1 1 1 和 5 5 5 都是必胜点。
那么点 1 1 1 和 5 5 5 都是必胜点。
由此断言:答案为非最大匹配必须点。
如果一个点 p p p 是非最大匹配必须点,那么存在一个最大匹配,使点 p p p 不是匹配点。在这个最大匹配上实行上述方案,小 AA 必胜。
我们发现,只需要对一个点尝试增广,如果增广出一条路径,长度与当前最大匹配的路径长度相等,那这个点就是一个非最大匹配必须点。
由于一个点可能在 X X X 部,也可能在 Y Y Y 部,分类讨论的话要写两个增广函数。可以将两部记录匹配点的数组 c x cx cx 和 c y cy cy 合并,统一为 c x y cxy cxy, c x y i cxy_i cxyi 记录点 i i i 对应的匹配点编号。这样的话需要建双向边,所以其实是用增大常数的代价换来较小的编程复杂度。
时间复杂度 O ( n 4 ) O(n^4) O(n4).
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 40005;//不能开太大,否则 memset 时会 TLE
int n, m, cnt = 0, fir[N], nxt[N], to[N], vis[N], cxy[N], p[105][105], tot = 0, xt, cans = 0;
char a[105][105];
int dx[5] = {0, 1, 0, -1};
int dy[5] = {1, 0, -1, 0};
struct node {int x, y;
} ans[N];
void ade(int u, int v) {cnt++, nxt[cnt] = fir[u], fir[u] = cnt, to[cnt] = v;cnt++, nxt[cnt] = fir[v], fir[v] = cnt, to[cnt] = u;
}
void getp() {//重标号for (int i = 1; i <= n; i++)for (int j = ((i & 1) ? 1 : 2); j <= m; j += 2)if (a[i][j] == '.')p[i][j] = ++tot;xt = tot;for (int i = 1; i <= n; i++)for (int j = ((i & 1) ? 2 : 1); j <= m; j += 2)if (a[i][j] == '.')p[i][j] = ++tot;
}
void ADE(int x, int y) {//将 (x,y) 与邻接点连边for (int i = 0; i < 4; i++) {int xx = x + dx[i], yy = y + dy[i];if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && a[xx][yy] == '.') ade(p[x][y], p[xx][yy]);}
}
int dfs(int r) {//找增广路径vis[r] = 1;for (int i = fir[r]; i; i = nxt[i])if (!vis[to[i]]) {vis[to[i]] = 1;if (!cxy[to[i]] || dfs(cxy[to[i]])) {cxy[cxy[r]] = 0, cxy[r] = to[i], cxy[to[i]] = r;return 1;}}return 0;
}
void match() {for (int i = 1; i <= xt; i++)if (!cxy[i])memset(vis, 0, sizeof(vis)), dfs(i);
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) scanf("%s", a[i] + 1);getp();for (int i = 1; i <= n; i++)for (int j = ((i & 1) ? 1 : 2); j <= m; j += 2)//只枚举偶点if (a[i][j] == '.')ADE(i, j);match();//先求一种最大匹配方案for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)if (a[i][j] == '.') {memset(vis, 0, sizeof(vis));if (!cxy[p[i][j]] || dfs(cxy[p[i][j]])) ans[++cans].x = i, ans[cans].y = j;}if (!cans) { printf("LOSE"); return 0; }//没有非匹配点printf("WIN\n");for (int i = 1; i <= cans; i++) printf("%d %d\n", ans[i].x, ans[i].y);return 0;
}
END
相关文章:

【题解】P4055 [JSOI2009] 游戏
link 题目大意 题目说得比较清楚。 题解 前置知识:二分图最大匹配、基础博弈论。 每个点只能走一次的四联通点阵,可以想到二分图匹配。 将其套路地奇偶分点,相邻两点连边(显然不能为 #)。 先求一个最大匹配。 …...

P1020 [NOIP1999 普及组] 导弹拦截
题目描述 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统…...

Makefile学习
什么是Makefile 使用 GCC 编译器在 Linux 进行 C 语言编译,通过在终端执行 gcc 命 令来完成 C 文件的编译,如果我们的工程只有一两个 C 文件还好,需要输入的命令不多,当文件有几十、上百甚至上万个的时候用终端输入 GCC 命令的方…...

2.4 随机变量函数的分布
学习目标: 学习随机变量函数的分布,我会采取以下步骤: 熟悉随机变量的基本概念和分布:在学习随机变量函数的分布之前,需要先掌握随机变量的基本概念和分布,包括离散型随机变量和连续性随机变量的概率密度…...

数据结构【一】:前缀表达式与后缀表达式的区别
在早期计息机系统中,由于没有括号规定运算顺序,因此,依靠出栈和入栈两种方式,限定元素和符号之间的关系确定了前缀表达式和后缀表达式两种运算方式,中缀表达式即为普通的运算表达式;注意,在栈结…...

搭建 PostgreSQL
端口:5432 代理备份端口:6432 下载 postgresql-15.0-1-windows-x64 乱码显示 配置环境变量 PGDATA数据目录位置 找到postgresql.conf文件, 修改参数 lc_messagesUTF8 max_connections 1000 shared_buffers4GB work_mem8MB 问题:…...

Nmap入门到高级【第四章】
预计更新Nmap基础知识 1.1 Nmap简介和历史 1.2 Nmap安装和使用方法 1.3 Nmap扫描技术和扫描选项 Nmap扫描技术 2.1 端口扫描技术 2.2 操作系统检测技术 2.3 服务和应用程序检测技术 2.4 漏洞检测技术 Nmap扫描选项 3.1 扫描类型选项 3.2 过滤器选项 3.3 探测选项 3.4 输出选项…...

c++正则表达式及其使用,超级详细
文章目录 概述正则表达式语法正则表达式操作std::regex_matchstd::regex_replacestd::regex_search 实例匹配邮箱替换 HTML 标签搜索 URL 总结 概述 正则表达式是一种用于匹配字符串的工具,可以在文本中查找特定的模式,并且可以快速地对字符串进行搜索和…...

【LeetCode: 剑指 Offer II 099. 最小路径之和 | 暴力递归 | DFS =>记忆化搜索=>动态规划】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...

Python OpenCV 计算机视觉:6~7
原文:OpenCV Computer Vision with Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,你最…...

LabView中数组的使用2-1
在LabView中,数组用来管理相同类型的数据。 1 在前面板中创建数组 1.1 创建空数组 在前面板中创建数组时,首先在前面板中点击鼠标右键,弹出“控件”对话框,之后选择“新式->数组、矩阵与簇->数组”,在前面板中…...

Android 10.0 系统systemui下拉通知栏的通知布局相关源码分析
1.前言 在android10.0的系统rom开发中,在进行systemui中的下拉通知栏的布局自定义的时候,对于原生systemui的 系统的下拉通知栏的通知布局的了解也是非常重要的,接下来就来分析下相关的下拉通知栏的通知布局的相关 源码流程,了解这些才方便对通知栏的布局做修改 2.系统…...
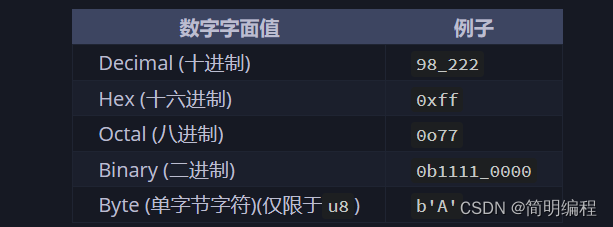
研读Rust圣经解析——Rust learn-3(变量与可变性,数据类型)
研读Rust圣经解析——Rust learn-3(变量与可变性,数据类型) 变量|常量与可变性变量声明案例为什么不可变变量可变(mut关键字)变量可变(覆盖) 常量声明 数据类型标量类型整型整型字面值整型溢出问…...

接口的多继承多实现
接口的多继承多实现 目录 接口的多继承多实现多继承(接口1 extends 接口2,接口3)多实现(实现类 实现 接口1,接口2)总结1.类与类的关系2.类和接口的关系3.接口与接口的关系 多继承(接口1 extends 接口2,接口…...

腾讯-iOS面试题-答案
一面 1、介绍一下实习的项目,任务分工,做了哪些工作?介绍实习内容 2、网络相关的:项目里面使用到什么网络库,用过ASIHTTP库吗 在iOS开发中,常用的网络库包括: URLSession:苹果官方提供的网络…...

SQL Server内存架构
2. 内存架构 所谓内存架构,这里是指SQL Server实例内存管理、使用与相关逻辑设计及实现等方面内容。更具体一点,就是讲SQL Server实例分配、管理和使用其内存空间的内部机制。本书1.1节中我们已经讲过,SQL Server实例包括多个内部机制各不相同的内存区域,在此,我们将讲解…...

有哪些功能强大,但是很小众的Python库呢?
Python生态系统中有很多小众但非常强大的库,一般,通俗的规律就是,越是高端,越小众,但是,高端不代表难学,只要理论到了,用起来照样嗖嗖的,以下是一些参考的高端小众库&…...

SpringBoot设计了哪些可拓展的机制?
SpringBoot核心源码 public SpringApplication(ResourceLoader resourceLoader, Class<?>... primarySources) { ...this.primarySources new LinkedHashSet(Arrays.asList(primarySources));// Servletthis.webApplicationType WebApplicationType.deduceFromClass…...
Layer组件多个iframe弹出层打开与关闭及参数传递
Layer官网地址:http://layer.layui.com/ 1、多个iframe弹出层(非嵌套) 1.打开iframe弹出层js代码 (1)示例一: content参数可传入要打开的页面,type参数传2,即可打开iframe类型的弹层…...
BearPi环境搭建及基本使用
这是一篇总结,一些坑的记录 具体教程请访问: BearPi-HM_Nano: 小熊派BearPi-HM Nano开发板基于HarmonyOS的源码 - Gitee.com 第一步:安装虚拟机 不做赘述 第二步:下载资源 这里要用到ubuntu的一些基础知识,不会的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
