【LeetCode: 剑指 Offer II 099. 最小路径之和 | 暴力递归 | DFS =>记忆化搜索=>动态规划】

🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🍎座右铭:人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯🎯

目录
- 题目链接
- 题目描述
- 求解思路&实现代码&运行结果
- 暴力递归 | DFS
- 求解思路
- 实现代码1
- 实现代码2
- 运行结果
- 记忆化搜索
- 求解思路
- 实现代码
- 运行结果
- 动态规划
- 求解思路
- 实现代码
- 运行结果
- 共勉
题目链接
剑指 Offer II 099. 最小路径之和
64. 最小路径和
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:一个机器人每次只能向下或者向右移动一步。
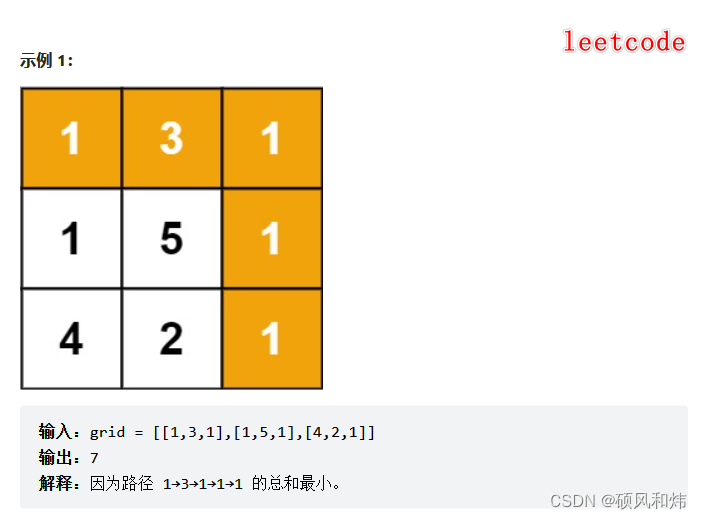
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
求解思路&实现代码&运行结果
暴力递归 | DFS
求解思路
- 通过读取题目的意思我们可以知道,从左上角位置开始,每次可以向下走,或者向右走,求最后到达右下角位置路径的最小值。
- 我们可以对题目进行一个简单的分析,如果此时我们是处于最后一行的,那么下次我们只能继续向右走,同理,如果我们此时是处理最后一列的,那么下次我们只能向下走。
- 上面是俩种特殊情况,然后是任意一个位置,任意一个位置的值可能来自左侧,也可能来自上侧,我们需要取得它们的最小值,然后加上当前位置的值,不断重复这个过程,直到目标节点。
实现代码1
注意,代码的实现方式可以有很多,大家根据自己的习惯来就好
class Solution {public int minPathSum(int[][] grid) {int m=grid.length,n=grid[0].length;return process(0,0,m,n,grid);}public int process(int x,int y,int m,int n,int[][] grid){if(x>=m||y>=n) return Integer.MAX_VALUE;if(x==m-1&&y==n-1) return grid[x][y];return Math.min(process(x,y+1,m,n,grid),process(x+1,y,m,n,grid))+grid[x][y];}
}
实现代码2
class Solution {int min=Integer.MAX_VALUE;public int minPathSum(int[][] grid) {int m=grid.length,n=grid[0].length;process(0,0,m,n,grid,0);return min;}public void process(int x,int y,int m,int n,int[][] grid,int sum){if(x>=m||y>=n) return;if(x==m-1&&y==n-1){min=Math.min(min,sum+grid[x][y]); return;}process(x,y+1,m,n,grid,sum+grid[x][y]);process(x+1,y,m,n,grid,sum+grid[x][y]);}
}
运行结果
大家不要看到时间超限就害怕,相反,看到这个我们更应该放心,这个是我们期待的结果。
记忆化搜索
求解思路
- 核心思路就是我们上面的求解过程,如果没有理解可以继续看上面的图解过程。
- 在原来的基础上加缓存表,将结果进行记录,避免重复计算。
实现代码
class Solution {public int minPathSum(int[][] grid) {int m=grid.length,n=grid[0].length;int[][] dp=new int[m][n];for(int i=0;i<m;i++) Arrays.fill(dp[i],-1);return process(0,0,m,n,grid,dp);}public int process(int x,int y,int m,int n,int[][] grid,int[][] dp){if(x>=m||y>=n) return Integer.MAX_VALUE;if(dp[x][y]!=-1) return dp[x][y];if(x==m-1&&y==n-1) return dp[x][y]=grid[x][y];return dp[x][y]=Math.min(process(x,y+1,m,n,grid,dp),process(x+1,y,m,n,grid,dp))+grid[x][y];}
}
运行结果
加个缓存表就是香,通过!
动态规划
求解思路
- 同理,核心求解思路我们上面已经讲过了,此处不同的是原来通过递归,此时我们通过dp数组和循环即可完成。
实现代码
继续改进!
class Solution {public int minPathSum(int[][] grid) {int m=grid.length,n=grid[0].length;int[][] dp=new int[m][n];dp[m-1][n-1]=grid[m-1][n-1];for(int i=m-2;i>=0;i--){dp[i][n-1]=dp[i+1][n-1]+grid[i][n-1];}for(int i=n-2;i>=0;i--){dp[m-1][i]=dp[m-1][i+1]+grid[m-1][i];}for(int x=m-2;x>=0;x--){for(int y=n-2;y>=0;y--){dp[x][y]=Math.min(dp[x][y+1],dp[x+1][y])+grid[x][y];}}return dp[0][0];}
}
运行结果
共勉
最后,我想送给大家一句一直激励我的座右铭,希望可以与大家共勉!


相关文章:

【LeetCode: 剑指 Offer II 099. 最小路径之和 | 暴力递归 | DFS =>记忆化搜索=>动态规划】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...

Python OpenCV 计算机视觉:6~7
原文:OpenCV Computer Vision with Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,你最…...

LabView中数组的使用2-1
在LabView中,数组用来管理相同类型的数据。 1 在前面板中创建数组 1.1 创建空数组 在前面板中创建数组时,首先在前面板中点击鼠标右键,弹出“控件”对话框,之后选择“新式->数组、矩阵与簇->数组”,在前面板中…...

Android 10.0 系统systemui下拉通知栏的通知布局相关源码分析
1.前言 在android10.0的系统rom开发中,在进行systemui中的下拉通知栏的布局自定义的时候,对于原生systemui的 系统的下拉通知栏的通知布局的了解也是非常重要的,接下来就来分析下相关的下拉通知栏的通知布局的相关 源码流程,了解这些才方便对通知栏的布局做修改 2.系统…...
研读Rust圣经解析——Rust learn-3(变量与可变性,数据类型)
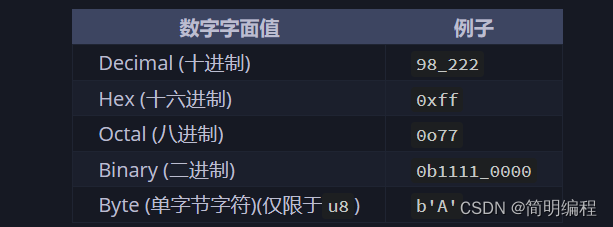
研读Rust圣经解析——Rust learn-3(变量与可变性,数据类型) 变量|常量与可变性变量声明案例为什么不可变变量可变(mut关键字)变量可变(覆盖) 常量声明 数据类型标量类型整型整型字面值整型溢出问…...

接口的多继承多实现
接口的多继承多实现 目录 接口的多继承多实现多继承(接口1 extends 接口2,接口3)多实现(实现类 实现 接口1,接口2)总结1.类与类的关系2.类和接口的关系3.接口与接口的关系 多继承(接口1 extends 接口2,接口…...

腾讯-iOS面试题-答案
一面 1、介绍一下实习的项目,任务分工,做了哪些工作?介绍实习内容 2、网络相关的:项目里面使用到什么网络库,用过ASIHTTP库吗 在iOS开发中,常用的网络库包括: URLSession:苹果官方提供的网络…...

SQL Server内存架构
2. 内存架构 所谓内存架构,这里是指SQL Server实例内存管理、使用与相关逻辑设计及实现等方面内容。更具体一点,就是讲SQL Server实例分配、管理和使用其内存空间的内部机制。本书1.1节中我们已经讲过,SQL Server实例包括多个内部机制各不相同的内存区域,在此,我们将讲解…...

有哪些功能强大,但是很小众的Python库呢?
Python生态系统中有很多小众但非常强大的库,一般,通俗的规律就是,越是高端,越小众,但是,高端不代表难学,只要理论到了,用起来照样嗖嗖的,以下是一些参考的高端小众库&…...

SpringBoot设计了哪些可拓展的机制?
SpringBoot核心源码 public SpringApplication(ResourceLoader resourceLoader, Class<?>... primarySources) { ...this.primarySources new LinkedHashSet(Arrays.asList(primarySources));// Servletthis.webApplicationType WebApplicationType.deduceFromClass…...
Layer组件多个iframe弹出层打开与关闭及参数传递
Layer官网地址:http://layer.layui.com/ 1、多个iframe弹出层(非嵌套) 1.打开iframe弹出层js代码 (1)示例一: content参数可传入要打开的页面,type参数传2,即可打开iframe类型的弹层…...
BearPi环境搭建及基本使用
这是一篇总结,一些坑的记录 具体教程请访问: BearPi-HM_Nano: 小熊派BearPi-HM Nano开发板基于HarmonyOS的源码 - Gitee.com 第一步:安装虚拟机 不做赘述 第二步:下载资源 这里要用到ubuntu的一些基础知识,不会的…...

算法笔记-换根DP
换根DP 一般是给定一棵不定根树,求以每个节点为根的一些信息。可以通过二次扫描: 第一次扫描,任选一点为根,在有根树上,自底向上转移第二次扫描,从上一次扫描的根开始,自顶向下计算 P3478 [P…...
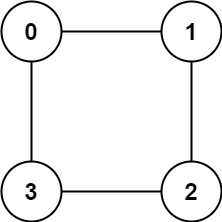
LeetCode 785. Is Graph Bipartite【DFS,二分图】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【微信小程序】-- 分包 - 独立分包 分包预下载(四十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

2.3 连续性随机变量
思维导图: 学习目标: 我会按照以下步骤学习连续型随机变量: 复习概率论的基础知识,包括概率、期望、方差等概念和公式,以及离散型随机变量的概率分布函数和概率质量函数的概念和性质。 学习连续型随机变量的概念和性…...
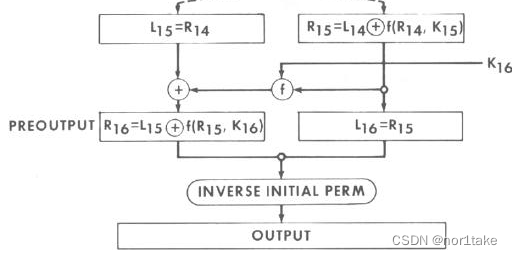
【DES详解】(一)处理input block(64 bits)
一、DES 加密算法总览 0-1、初识置换 IP(Initial Permutation) 输入:明文(64 bits) 过程:初识置换 输出:处理后的明文permuted input(64 bits) 首先,对需要解…...

redis笔记——三种特殊的数据结构
三种特殊数据类型 geospatial(地理位置) 用于定位,附近的人,距离计算 添加元素 geoadd key 经度 纬度 描述名称,可一次添加多个元素 127.0.0.1:6379> geoadd china:city 113.28 23.12 guangzhou (integer) 1 1…...

网络安全之编码加密算法
网络安全之编码加密算法 一、ROT5/13/18/47编码转换二、MD5加密 一、ROT5/13/18/47编码转换 ROT5、ROT13、ROT18、ROT47 编码是一种简单的码元位置顺序替换暗码,属于凯撒密码的一种。此类编码具有可逆性,可以自我解密,主要用于应对快速浏览&…...

mp4视频无法播放的解决方法
mp4视频是我们日常工作生活中经常会遇到的视频格式,但如果遇到重要的mp4视频无法播放了,该怎么办呢?有mp4视频无法播放的解决方法吗?下面小编为大家整理了这个问题产生的原因以及相应的解决方法,让我们看一看。 什么情况下会导致mp4视频无法…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
