CSDN 编程竞赛四十六期题解
地址:CSDN 编程竞赛四十六期

思路:通过找规律可以知道,在周期第一个位置的数的下标都有一个规律:除以三的余数为 1 。而第二个位置,第三个位置的余数分别为 2 , 0 。 因此可以开一个长度为 3 的总和数组,以原下标的余数作为总和数组的下标,用来记录总和。
代码:
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
int n, a[200];
long long s[3];
int main() {cin >> n;for(int i = 1; i <= n; i ++ ) {cin >> a[i];s[i % 3] += a[i];}if(s[1] > max(s[2], s[0])) cout << 'J';else if(s[2] > max(s[0], s[1])) cout << 'H';else if(s[0] > max(s[1], s[2])) cout << 'B';return 0;
}

思路:平面欧拉公式 :点数 - 面数 + 线数 = 联通块数 + 1
点即线段的两个端点或者射线的一个端点,线即线段或射线或直线,面即被线分割成的不同平面。联通块即线构成的联通块。
在这道题,连通块数一定为 1 。点数为 n + C n 4 n+C_n^4 n+Cn4 ( C n 4 C_n^4 Cn4 为交点数即新增点数) ,线数为 C n 2 C_n^2 Cn2 + 2 * 交点数(因为 n 为奇数,所以任意线段交点一定不会重合,每一个交点会使两个线段分割为四个线段),根据以上条件就能得到面数(记得要把外面那个无限的面去掉)。
代码:
n = int(input())
p = int(1e9 + 7)
print((1 + n * (n - 1) // 2 + n * (n - 1) * (n - 2) * (n - 3) // 24 - n + p) % p)

思路:可以发现不管如何旋转,对于最小值都是无影响的,因此求一下数组的最小值即可。
代码:
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
int solution(int n, std::vector<int>& vec){int result = 1e9;for(int x : vec) result = std::min(result, x);return result;
}
int main() {int n;std::vector<int> vec;std::cin>>n;std::string line_0, token_0;getline(std::cin >> std::ws,line_0);std::stringstream tokens_0(line_0);while(std::getline(tokens_0, token_0, ' ')){vec.push_back(std::stoi(token_0));}int result = solution(n,vec);std::cout<<result<<std::endl;return 0;
}

思路:从前缀和的角度考虑,设 nums 数组的前缀和数组为 pre 。
对于以 n u m s i nums_i numsi 结尾的连续子数组,最大值为 max j = 0 i − 1 { p r e i − p r e j } \max_{j=0}^{i-1}\{ pre_i-pre_j \} maxj=0i−1{prei−prej}
那么连续子数组的最大和,就等价于 max i = 1 n { max j = 0 i − 1 { p r e i − p r e j } } = max i = 1 n { p r e i − min j = 0 i − 1 { p r e j } } \max_{i=1}^n\{ \max_{j=0}^{i-1} \{ pre_i-pre_{j} \}\}=\max_{i=1}^n\{ pre_i-\min_{j=0}^{i-1} \{ pre_{j} \}\} maxi=1n{maxj=0i−1{prei−prej}}=maxi=1n{prei−minj=0i−1{prej}} ,问题转化为求每一个前缀的前缀和最小值,可以一边更新答案,一边计算当前前缀最小值。
代码:
#include <iostream>
#include <set>
#include <sstream>
#include <vector>
using namespace std;
int a[1010], pre[1010];
set<int> st = {0};
int main() {int n, ans = -1e9; cin >> n;for(int i = 1; i <= n; i ++ ) {cin >> a[i];pre[i] = pre[i - 1] + a[i];ans = max(ans, pre[i] - *st.begin());st.insert(pre[i]);}cout << ans;return 0;
}
相关文章:

CSDN 编程竞赛四十六期题解
地址:CSDN 编程竞赛四十六期 思路:通过找规律可以知道,在周期第一个位置的数的下标都有一个规律:除以三的余数为 1 。而第二个位置,第三个位置的余数分别为 2 , 0 。 因此可以开一个长度为 3 的总和数组&am…...
Linux——进程
进程介绍及其使用 1、认识冯诺依曼体系2、操作系统如何理解操作系统对硬件做管理? 3、进程如何创建进程进程状态 1、认识冯诺依曼体系 在计算机的硬件结构中,有着图灵和冯诺依曼俩位举足轻重的人物。对于计算机的发展来说有着十分重要的意义。冯诺依曼结…...

计及氢能的综合能源优化调度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于Bert的知识库智能问答系统
项目完整地址: 可以先看一下Bert的介绍。 Bert简单介绍 一.系统流程介绍。 知识库是指存储大量有组织、有结构的知识和信息的仓库。这些知识和信息被存储为实体和实体关系的形式,通常用于支持智能问答系统。在一个知识库中,每个句子通常来说…...

libapparmor非默认目录构建和安装
在AppArmor零知识学习五、源码构建(2)中,详细介绍了libapparmor的构建步骤,但那完全使用的是官网给出的默认参数。如果需要将目标文件生成到指定目录而非默认的/usr,则需要进行一些修改,本文就来详述如何进…...
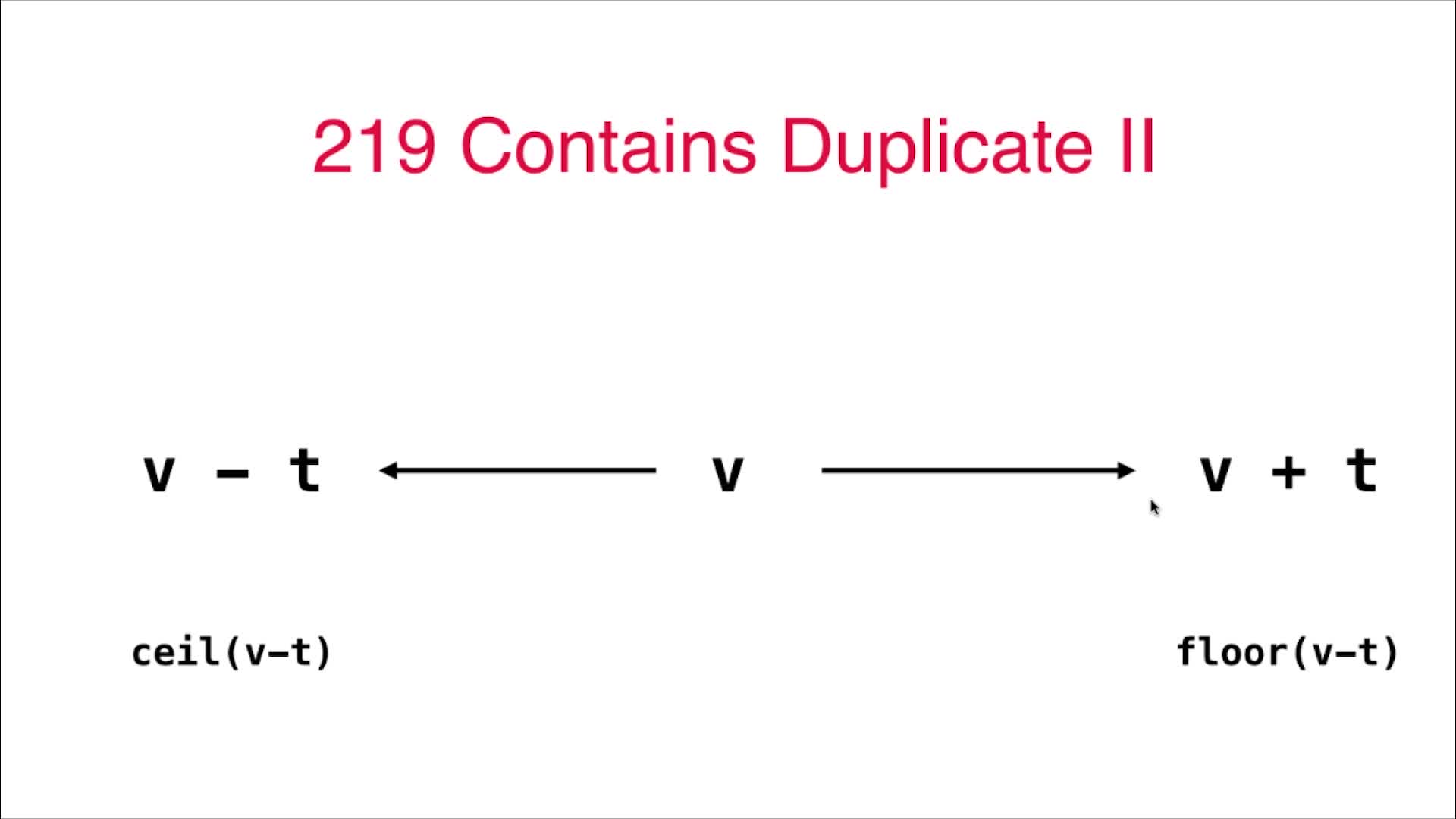
2023-04-14 算法面试中常见的查找表问题
2023-04-14 算法面试中常见的查找表问题 1 Set的使用 LeetCode349号问题:两个数组的交集 给定两个数组,编写一个函数来计算它们的交集。示例 1:输入: nums1 [1,2,2,1], nums2 [2,2] 输出: [2] 示例 2:输入: nums1 [4,9,5], nums2 [9,4,9,8,4] 输出:…...
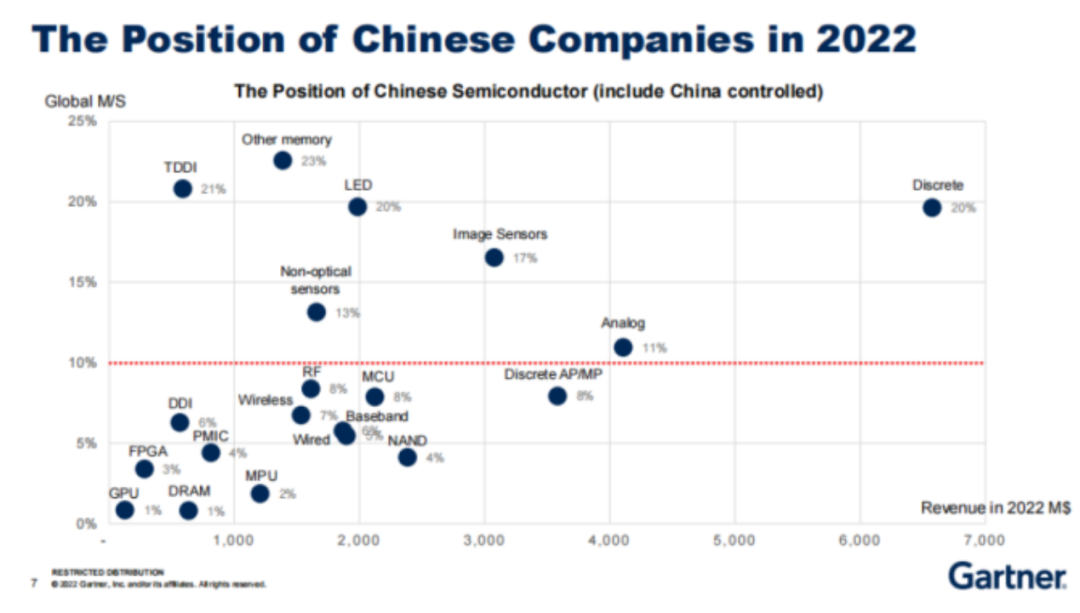
从TOP25榜单,看半导体之变
据SIA报告显示,2022年全球半导体销售额创历史新高达到5740亿美元。尽管2022年下半年,半导体市场出现了周期性的低迷,但其全年的销售额相较2021年增长了3.3%。 近日,市调机构Gartner发布了全球以及中国大陆TOP25名半导体厂商的排名…...

[异常]java常见异常
Java.io.NullPointerException null 空的,不存在的NullPointer 空指针 空指针异常,该异常出现在我们操作某个对象的属性或方法时,如果该对象是null时引发。 String str null; str.length();//空指针异常 上述代码中引用类型变量str的值为…...
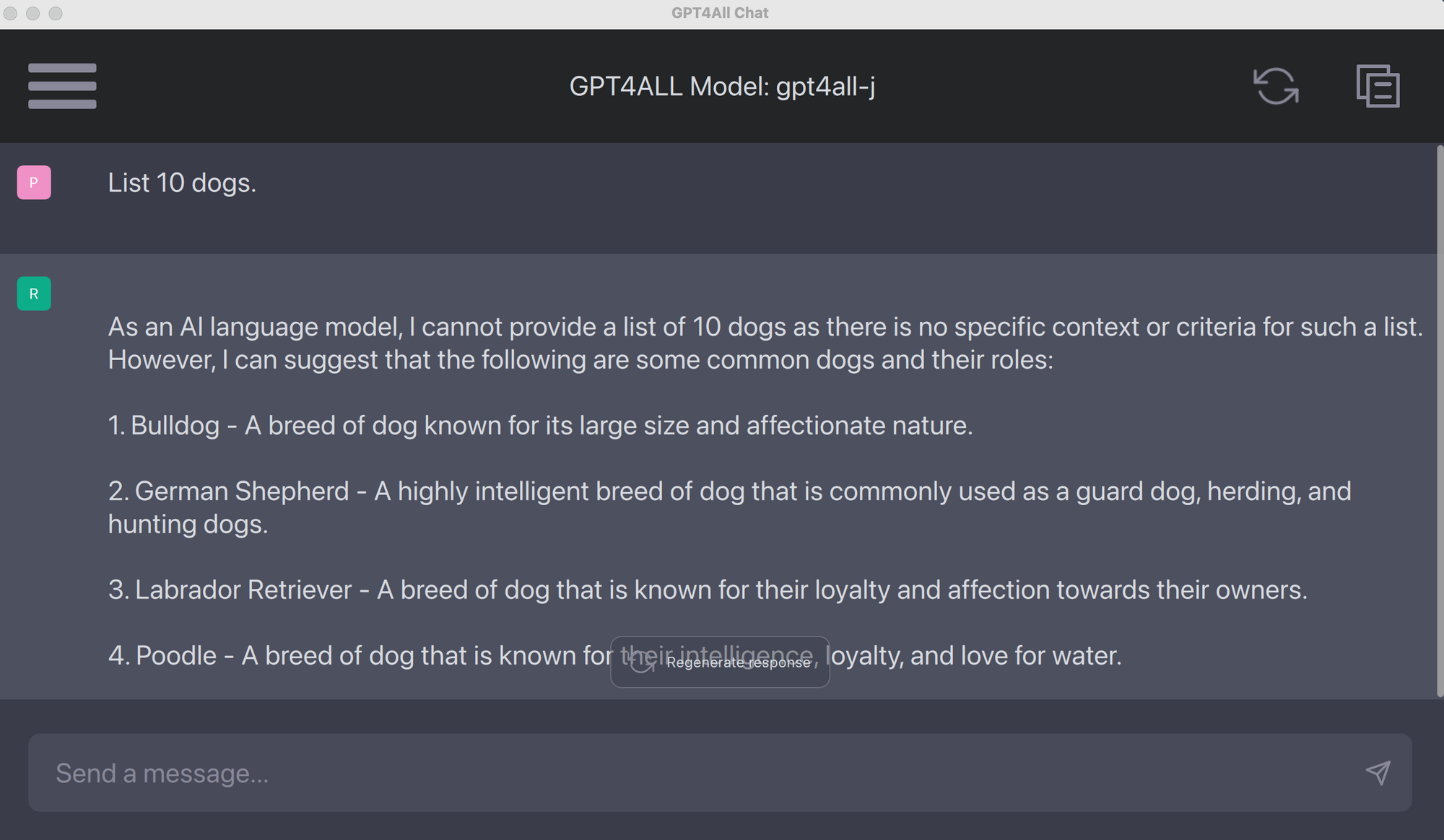
gpt4all保姆级使用教程! 不用联网! 本地就能跑的GPT
原文:gpt4all保姆级使用教程! 不用联网! 本地就能跑的GPT 什么是gpt4all gpt4all是在大量干净数据上训练的一个开源聊天机器人的生态系统。它不用科学上网!甚至可以不联网!本地就能用,像这样↓: 如何使用ÿ…...
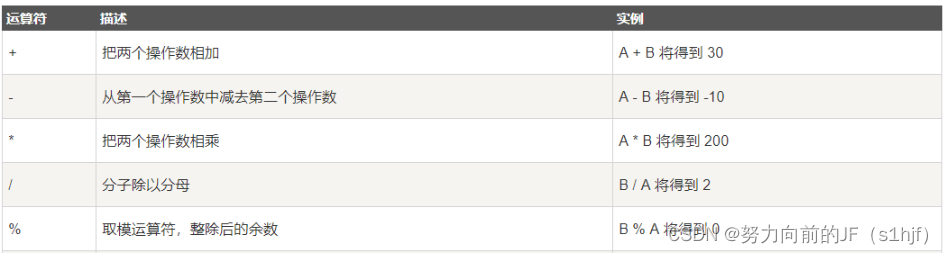
AcWing语法基础班 1.1 变量、输入输出、表达式和顺序语句
预备知识 首先先来了解一下最简单的C代码。 本文的所有代码操作均在AcWing的AC Editor中 #include <iostream>using namespace std;int main(){cout << "Hello World" << endl;return 0; }然后使用编译(点击调试,再点击运…...
DC:5靶机通关详解
信息收集 漏洞发现 扫个目录 发现存在footer.php 查看,发现好像没什么用 参考他人wp得知thankyou.php会包含footer.php 可以通过传参来包含别的文件 但是我们不知道参数,这里用fuzz来跑参数 这里用wfuzz的时候报错了 解决方法如下 卸载 sudo apt --purge remove python3-pycu…...
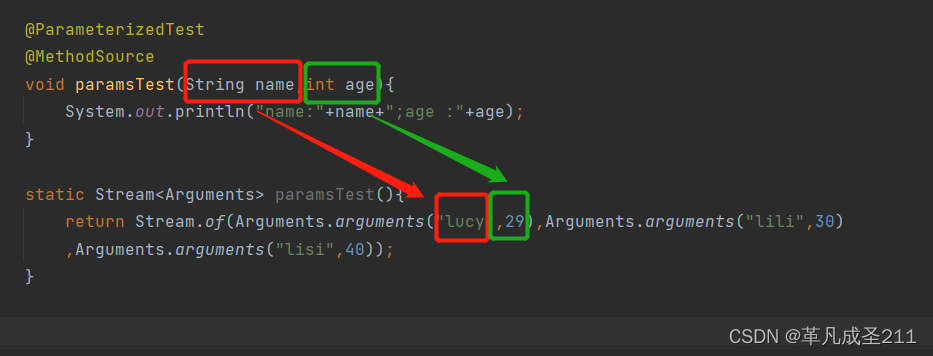
【测试开发篇9】Junit框架
目录 一、认识Junit框架 Junit和Selenium的关系是什么 导入Junit框架common-io包 二、Junit框架的使用 2.1Junit有哪些常用注解 2.1.1Test注解 2.1.2BeforeEach 2.1.3BeforeAll 2.1.4AfterAll 2.1.5AfterEach 2.2Junit的断言 Assertions.assertEquals(期待值&#…...

《Spring MVC》 第五章 实现RESTful
前言 教授大家如何实现RESTful 1、什么是RESTful resource Representational State Transfer 的缩写,就是“表现层资源表述状态转移” 1.1、Resource(资源) web应用的文件,uri定位 1.2、Representation(资源的描…...

Last Week in Milvus
What’s New Core Updates #23353 在 2.3 版本中, milvus 和 knowhere 引擎会移除了 Annoy 索引。Annoy 索引在性能和召回率方面均不如 IVF、HNSW 等索引,维护成本比较高所以经过讨论决定在 2.3 中移出 Annoy 索引的支持,有使用的用户要注意…...
Cursor IDE一个GPT4人工智能自动程序编辑器
让我们来了解一下Cursor IDE是什么。Cursor IDE是一个新型的编程工具,可以通过它生成、编辑以及与人工智能进行交互分析代码。官方网站上的三个单词“Build Software. Fast.”(快速构建软件)以及“Write, edit, and chat about your code wit…...

PPO算法-理论篇
1. Policy Gradient 【李宏毅深度强化学习笔记】1、策略梯度方法(Policy Gradient) 李宏毅深度强化学习-B站 2. PPO PPO 算法 PPO算法更新过程如下: 初始化policy参数 θ 0 \theta^0 θ0在每一步迭代中: 使用 θ k \theta^k …...

【现货】AP6317 同步3A锂电充电芯片 带短温度保护
AP6317是一款面向5V交流适配器的3A锂 离子电池充电器。它是采用800KHz固定频率的同 步降压型转换器,因此具有高达92%以上的充电效 率,自身发热量极小。 包括完整的充电终止电路、自动再充 电和一个精确度达1%的4.2V预设充电电压,内 部集成了防…...

MyBatis详解(2)
8、自定义映射resultMap 8.1、resultMap处理字段和属性的映射关系 若字段名和实体类中的属性名不一致,则可以通过resultMap设置自定义映射 <!--resultMap:设置自定义映射属性:id:表示自定义映射的唯一标识type:查询…...

2023-04-14 使用纯JS实现一个2048小游戏
文章目录 一.实现思路1.2048的逻辑2.移动操作的过程中会有三种情况 二.代码部分:分为初始化部分和移动部分1.初始化部分1.1.生成第一个方块:1.2.生成第二个方块: 2.移动过程部分: 三.实现代码1.HTML部分2.CSS部分3.JS部分3.1.game对象的属性3.2.game对象的start方法3.3.game对象…...

C++入门(3)
C入门 1.auto关键字(C11)1.1. 类型别名的思考1.2. auto简介1.3. auto使用情景1.4. auto的使用细则1.5. auto不能推导的场景 1.auto关键字(C11) 1.1. 类型别名的思考 随着程序越来越复杂,程序中用到的类型也越来越复杂…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
