时序分析 49 -- 贝叶斯时序预测(一)
贝叶斯时序预测(一)
时序预测在统计分析和机器学习领域一直都是一个比较重要的话题。在本系列前面的文章中我们介绍了诸如ARIMA系列方法,Holt-Winter指数平滑模型等多种常用方法,实际上这些看似不同的模型和方法之间都具有千丝万缕的联系,包括我们一直没有涉及的最复杂的模型LSTM(Long Short Term Memory)。在实际的时序数据分析工作中,你会发现在通常境况下简单模型都比复杂模型更为有效。本文开始讨论另一套时序预测体系:Bayes 时序预测方法。这套方法的背后原理可以很简单,但也可以很深,我们不如从一个例子开始,先积累一些直觉和经验,后续系列会展开理论部分的讨论。
贝叶斯时序预测通常不会预测时序点,而是给出时序点的分布,但如果希望预测时序点,你可以简单取该分布的均值或者中位数。
贝叶斯定理回顾
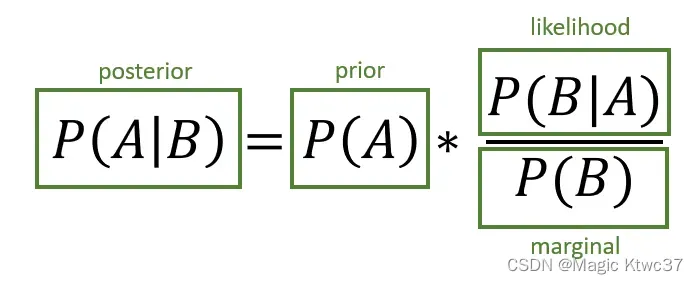
上图展示了贝叶斯定理的基本结构,这个定理可以认为是机器学习领域最重要的定理了,个人认为没有之一。
让我们来简单回顾一下这个定理的核心内容,
-
P ( A ) P(A) P(A) ,是事件 A A A的先验概率,可以理解为在没有任何具体的数据支持下,我们对事件 A A A发生的概率的直觉,也可称为prior belief(先验信念)。先验信念表示了我们对事件 A A A发生概率的主观理解。
-
P ( B ) P(B) P(B),是事件 B B B的概率,在贝叶斯定理中一般称为边缘概率(marginal)。
-
P ( A ∣ B ) P(A|B) P(A∣B),是当事件 B B B发生时事件 A A A发生的条件概率,在贝叶斯定理中称为后验概率(posterior)。
-
P ( B ∣ A ) P(B|A) P(B∣A),适当事件 A A A发生时事件 B B B发生的条件概率,在贝叶斯定理中称为似然性(likelihood)。
我们可以这样理解贝叶斯公式:首先定义一个我们对某个事件的主观理解的先验分布,然后通过数据和事实我们得到似然性,条件于边缘概率后得到后延概率。 通俗来说,我们对一个事情有一个信念,当我们看到与这个事情有关的数据和事实后,我们会更新这个信念。举个例子来说,例如我们有一个硬币,我们相信随机抛这个硬币,落地时正面朝上的概率时1/2。但事实上这个硬币由于制造工艺的随机性导致其正面朝上的概率为2/3,当我们做抛硬币实验时,随着我们观察到正面朝上的概率大于1/2,我们对这件事情的信念会随着事实而变化。
关于贝叶斯定理,日后我们还会做进一步讨论,尝试从其他维度更深一步理解这个重要定理。
贝叶斯时序预测
贝叶斯时序预测模型的一种最常用的方法称为:DGLM(Dynamic Generalized Linear Model),既动态泛化线性模型,这里
-
动态,模型系数会随时间变化而变化。
-
泛化,过观察的分布可以是多种分布,例如正态分布、泊松分布、伯努利分布、二项式分布等。
-
线性,预测值既系数与预测变量的乘积的线性组合。
此模型的关键要素为:
λ t = F t θ t \lambda_t=F_t \theta_t λt=Ftθt
-
λ t \lambda_t λt是线性预测变量
-
θ r \theta_r θr是状态向量,DGLM的系数融入到状态向量中,实际建模中此向量由一些组件组成,例如趋势、回归性、季节、节假日和特殊事件等。
-
F t F_t Ft是回归向量
这些变量都会有对应的折现因子,折现因子是在构建模型中由我们设定的,它表示我们给当先信息和历史信息所分配的权重。
Python 简单例子
读入数据和所需包
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as dt
from pybats.analysis import analysis
from pybats.point_forecast import mediandf = pd.read_csv('airpassengers.csv')# Changing the datatype
df["Month"] = pd.to_datetime(df['Month'], format='%Y-%m')# Setting the Date as index
df = df.set_index('Month')Y = df['#Passengers'].values
pybats为贝叶斯时许预测提供了很多参数,我们先来简单看一下
k = 1 # 向前预测一步
forecast_start = 0 # 预测从时间零点开始
forecast_end = len(df)-1 # 预测在数据最后结束mod, samples = analysis(Y,family="poisson", # 使用泊松分布forecast_start=forecast_start,forecast_end=forecast_end,k=k,nsamps=100, # 每个月取一百个样本prior_length=6, # 取6个点来定义先验分布rho=.9, # 随机效用扩展deltrend=0.5, # 趋势折现因子delregn=0.9 # 回归折现因子
)forecast = median(samples) # 预测
参数解释:
- family=”possion“: 我们可尝试使用泊松分布对正整数建模;使用normal对连续实数;使用bernoulli对0-1;使用binomial对bernoulli的加总和。
- nsamps=100:定义样本的数量,通过此样本可得到信任区间(credibale interval)和点估计(point estimate)
- prior_length=6:构造先验分布的点的数量,这个数值越大说明使用时序开始数据来建模先验分布的观测值越多
- rho=.9:随机效用扩展,这个参数增加了预测的波动
# Plotting
fig, ax = plt.subplots(1,1, figsize=(8, 6))
ax = plot_data_forecast(fig, ax, Y, forecast, samples,dates=df.index)
ax = ax_style(ax, ylabel='Sales', xlabel='Time',legend=['Forecast', 'Passengers', 'Credible Interval'])
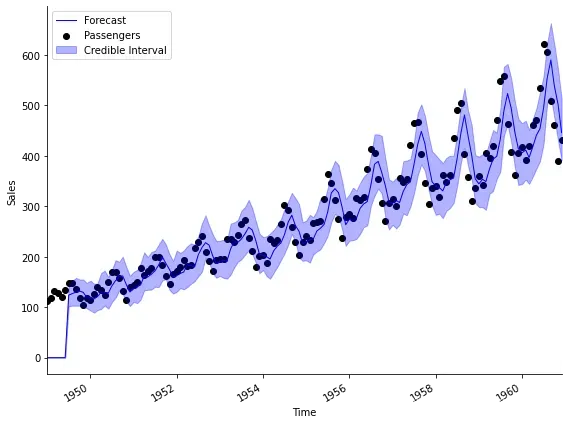
注意,上图中开始的水平线表明了建立先验分布所使用的月数,所以这里没有开始预测。 可以使用analysis函数来评估预测效果和对数据的拟合程度。
就这份数据而言,看上去拟合得不错,但我们需要知道
-
这个例子实际上不是预测,只能算是”事后诸葛亮“
-
这个数据集实际上非常好,有比较强的趋势和季节成分
PyBATS还有很多其他功能我们没有在这里演示,例如: -
增加节假日和特殊事件
-
深一步使用DGLM
-
使用隐含因子(latent factors),例如增加机票的平均价格来优化乘客人数的预测过程。
这只是个非常简单且不太完整的例子,如开头所言,这个例子只能给我们一些感性认识,后续笔者会分享更多关于这个主题的深层次的讨论和实践。
相关文章:

时序分析 49 -- 贝叶斯时序预测(一)
贝叶斯时序预测(一) 时序预测在统计分析和机器学习领域一直都是一个比较重要的话题。在本系列前面的文章中我们介绍了诸如ARIMA系列方法,Holt-Winter指数平滑模型等多种常用方法,实际上这些看似不同的模型和方法之间都具有千丝万缕…...

从传统管理到智慧水务:数字化转型的挑战与机遇
概念 智慧水务是指利用互联网、物联网、大数据、人工智能等技术手段,将智能化、信息化、互联网等技术与水务领域相结合,通过感知、传输、处理水质、水量、水价等数据信息,对水资源进行全面监测、综合管理、智能调度和优化配置的智能化水务系…...
ROS学习第十八节——launch文件(详细介绍)
1.概述 关于 launch 文件的使用已经不陌生了,之前就曾经介绍到: 一个程序中可能需要启动多个节点,比如:ROS 内置的小乌龟案例,如果要控制乌龟运动,要启动多个窗口,分别启动 roscore、乌龟界面节点、键盘控制节点。如果…...
javaweb在校大学生贷款管理系统ns08a9
1系统主要实现:学生注册、填写详细资料、申请贷款、学校审核、银行审核、贷后管理等功能, (1) 学生注册:学生通过注册用户,提交自己的详细个人资料,考虑现实应用中的安全性,资料提交后不可修改;…...
分布式之搜索解决方案es
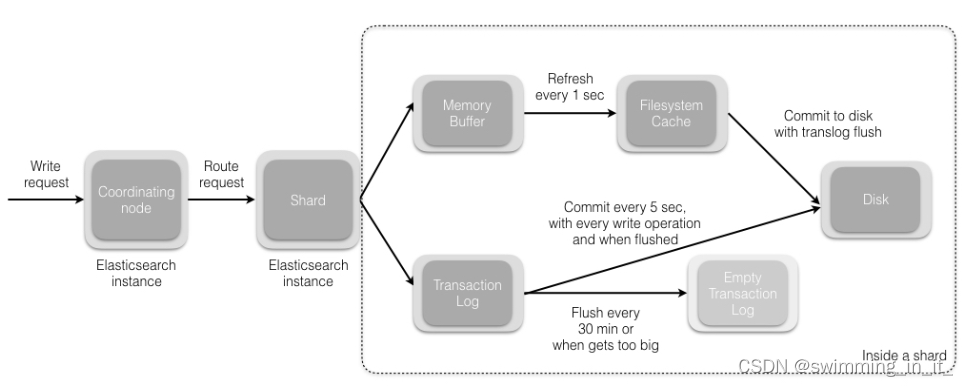
一 ES初识 1.1 概述 ElasticSearch:是基于 Lucene 的 Restful 的分布式实时全文搜索引擎,每个字段都被索引并可被搜索,可以快速存储、搜索、分析海量的数据。是ELK的一个组成,是一个产品,而且是非常完善的产品,ELK代表…...

CSDN 编程竞赛四十六期题解
地址:CSDN 编程竞赛四十六期 思路:通过找规律可以知道,在周期第一个位置的数的下标都有一个规律:除以三的余数为 1 。而第二个位置,第三个位置的余数分别为 2 , 0 。 因此可以开一个长度为 3 的总和数组&am…...
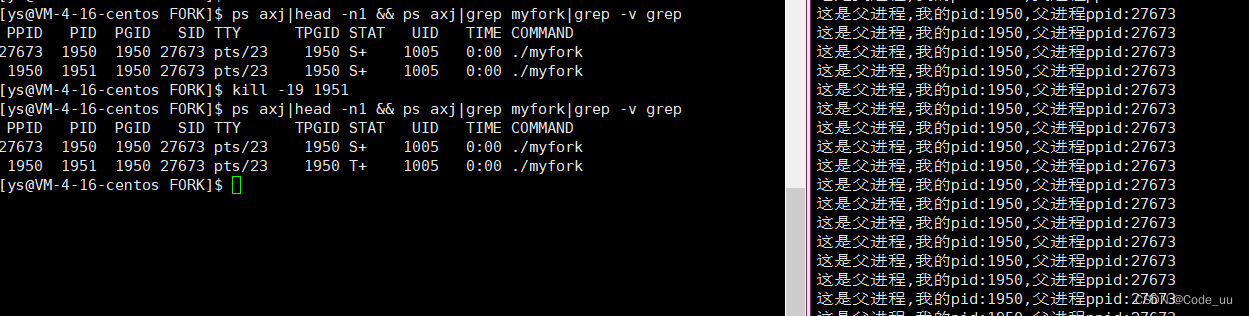
Linux——进程
进程介绍及其使用 1、认识冯诺依曼体系2、操作系统如何理解操作系统对硬件做管理? 3、进程如何创建进程进程状态 1、认识冯诺依曼体系 在计算机的硬件结构中,有着图灵和冯诺依曼俩位举足轻重的人物。对于计算机的发展来说有着十分重要的意义。冯诺依曼结…...

计及氢能的综合能源优化调度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于Bert的知识库智能问答系统
项目完整地址: 可以先看一下Bert的介绍。 Bert简单介绍 一.系统流程介绍。 知识库是指存储大量有组织、有结构的知识和信息的仓库。这些知识和信息被存储为实体和实体关系的形式,通常用于支持智能问答系统。在一个知识库中,每个句子通常来说…...

libapparmor非默认目录构建和安装
在AppArmor零知识学习五、源码构建(2)中,详细介绍了libapparmor的构建步骤,但那完全使用的是官网给出的默认参数。如果需要将目标文件生成到指定目录而非默认的/usr,则需要进行一些修改,本文就来详述如何进…...
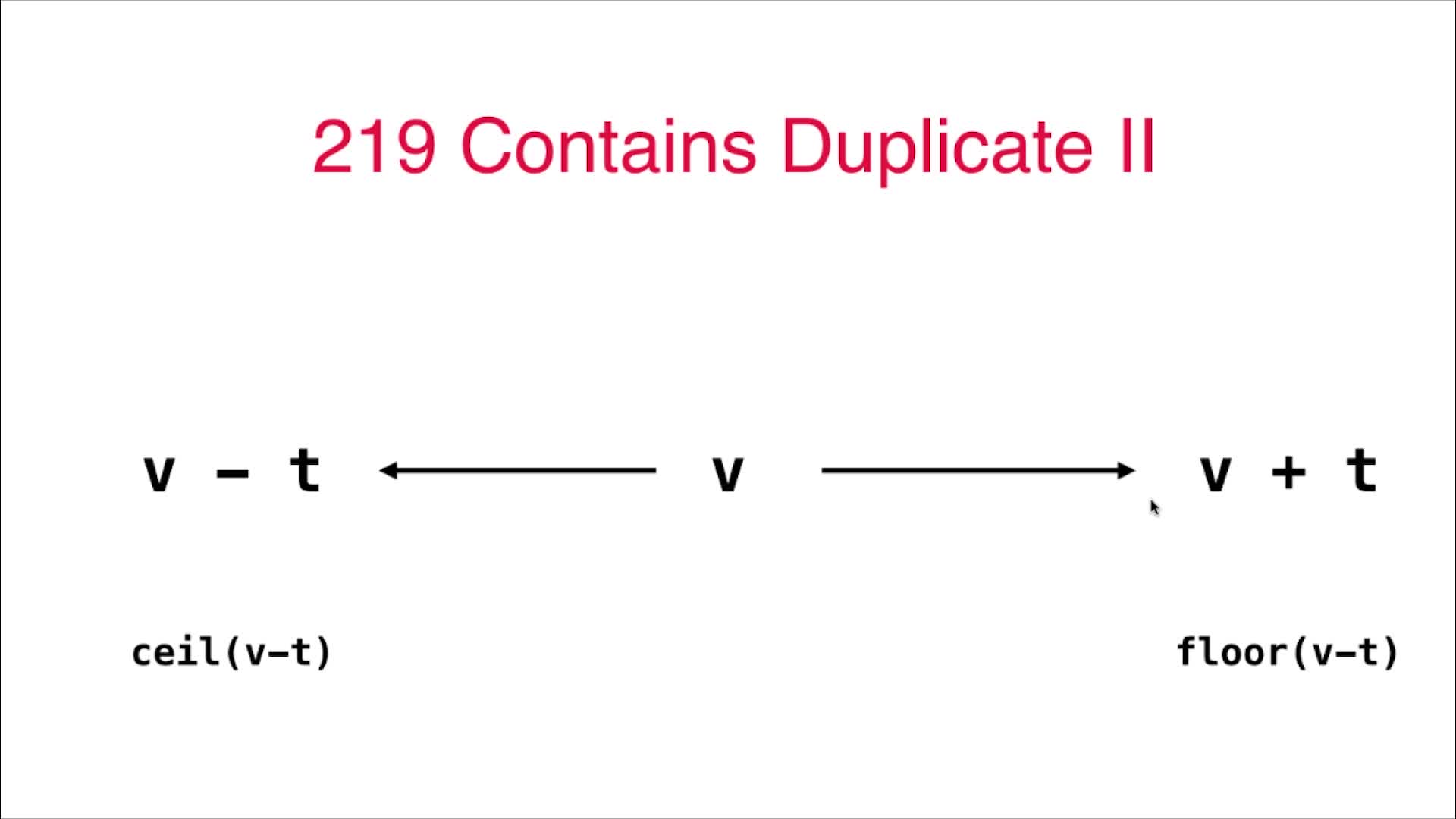
2023-04-14 算法面试中常见的查找表问题
2023-04-14 算法面试中常见的查找表问题 1 Set的使用 LeetCode349号问题:两个数组的交集 给定两个数组,编写一个函数来计算它们的交集。示例 1:输入: nums1 [1,2,2,1], nums2 [2,2] 输出: [2] 示例 2:输入: nums1 [4,9,5], nums2 [9,4,9,8,4] 输出:…...
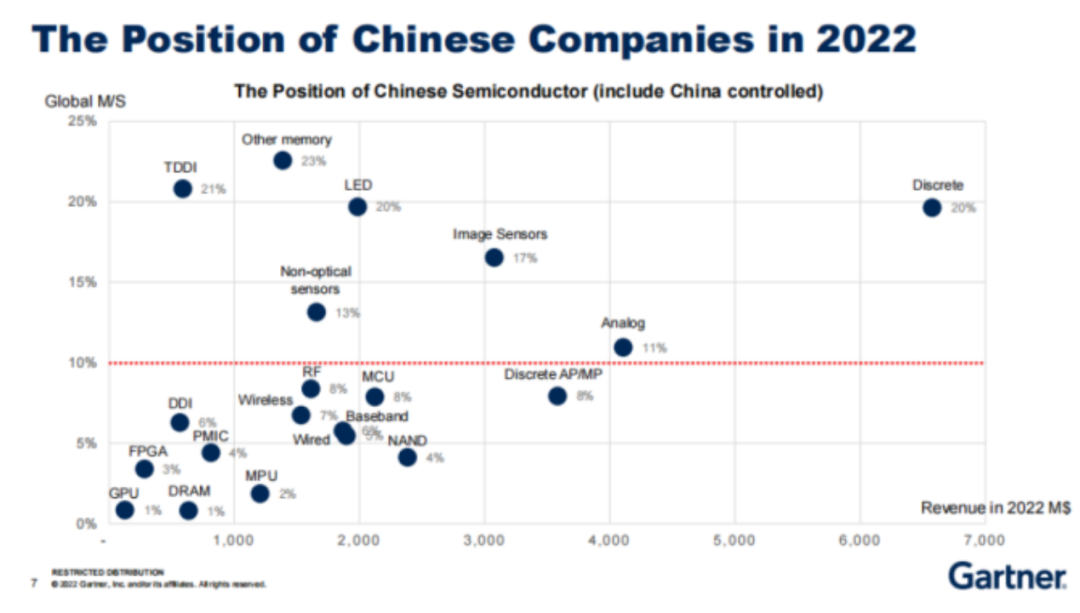
从TOP25榜单,看半导体之变
据SIA报告显示,2022年全球半导体销售额创历史新高达到5740亿美元。尽管2022年下半年,半导体市场出现了周期性的低迷,但其全年的销售额相较2021年增长了3.3%。 近日,市调机构Gartner发布了全球以及中国大陆TOP25名半导体厂商的排名…...

[异常]java常见异常
Java.io.NullPointerException null 空的,不存在的NullPointer 空指针 空指针异常,该异常出现在我们操作某个对象的属性或方法时,如果该对象是null时引发。 String str null; str.length();//空指针异常 上述代码中引用类型变量str的值为…...
gpt4all保姆级使用教程! 不用联网! 本地就能跑的GPT
原文:gpt4all保姆级使用教程! 不用联网! 本地就能跑的GPT 什么是gpt4all gpt4all是在大量干净数据上训练的一个开源聊天机器人的生态系统。它不用科学上网!甚至可以不联网!本地就能用,像这样↓: 如何使用ÿ…...
AcWing语法基础班 1.1 变量、输入输出、表达式和顺序语句
预备知识 首先先来了解一下最简单的C代码。 本文的所有代码操作均在AcWing的AC Editor中 #include <iostream>using namespace std;int main(){cout << "Hello World" << endl;return 0; }然后使用编译(点击调试,再点击运…...
DC:5靶机通关详解
信息收集 漏洞发现 扫个目录 发现存在footer.php 查看,发现好像没什么用 参考他人wp得知thankyou.php会包含footer.php 可以通过传参来包含别的文件 但是我们不知道参数,这里用fuzz来跑参数 这里用wfuzz的时候报错了 解决方法如下 卸载 sudo apt --purge remove python3-pycu…...
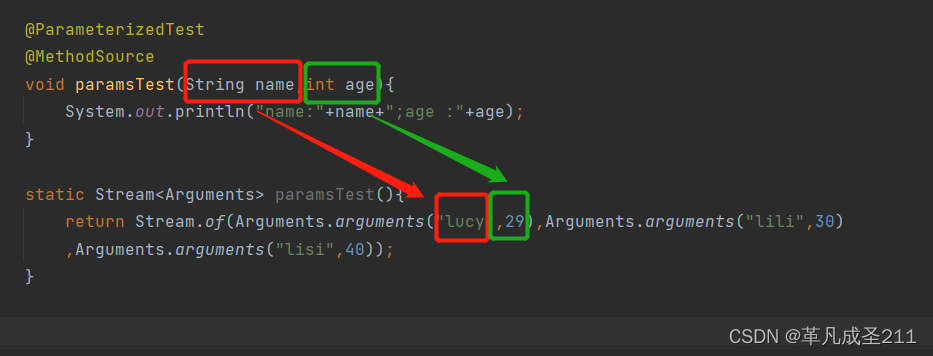
【测试开发篇9】Junit框架
目录 一、认识Junit框架 Junit和Selenium的关系是什么 导入Junit框架common-io包 二、Junit框架的使用 2.1Junit有哪些常用注解 2.1.1Test注解 2.1.2BeforeEach 2.1.3BeforeAll 2.1.4AfterAll 2.1.5AfterEach 2.2Junit的断言 Assertions.assertEquals(期待值&#…...

《Spring MVC》 第五章 实现RESTful
前言 教授大家如何实现RESTful 1、什么是RESTful resource Representational State Transfer 的缩写,就是“表现层资源表述状态转移” 1.1、Resource(资源) web应用的文件,uri定位 1.2、Representation(资源的描…...

Last Week in Milvus
What’s New Core Updates #23353 在 2.3 版本中, milvus 和 knowhere 引擎会移除了 Annoy 索引。Annoy 索引在性能和召回率方面均不如 IVF、HNSW 等索引,维护成本比较高所以经过讨论决定在 2.3 中移出 Annoy 索引的支持,有使用的用户要注意…...
Cursor IDE一个GPT4人工智能自动程序编辑器
让我们来了解一下Cursor IDE是什么。Cursor IDE是一个新型的编程工具,可以通过它生成、编辑以及与人工智能进行交互分析代码。官方网站上的三个单词“Build Software. Fast.”(快速构建软件)以及“Write, edit, and chat about your code wit…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
