辉煌优配|军工板块逆市上涨,16只概念股已披露一季度业绩预喜
 今日,军工股逆市上涨。
今日,军工股逆市上涨。
4月21日,A股三大股指低开低走,半导体、AI使用、信创工业、软件等科技属性概念领跌,国防军工、食品饮料和电力设备等板块上涨。
工业互联网中心工业规模超1.2万亿元
据央视新闻报道,本年是《工业互联网创新发展行动方案(2021-2023年)》(以下简称《方案》)实施最后一年。《方案》提出,这3年要完成工业互联网全体发展阶段跃升。工信部透露,我国工业互联网中心工业规模超过1.2万亿元,较上年增加15.5%。
目前,工业互联网掩盖45个国民经济大类,掩盖工业大类的85%以上。一季度,工业和信息化部发布了5G工厂、工业互联网园区、公共服务渠道等218个工业互联网试点示范项目,打造一批使用实践样板,加快数字化转型。
国内工业软件的发展以海外高端工业软件厂商做实施交给起步,当前自研工业软件开端逐渐对海外形成替代,同时工业互联网发展开端追逐国际步伐。大局来看,全球工业的数字化转型尚处于部分中心运营环节之间的协同互通阶段,未来仍大有可为。
早盘,工业互联网概念股以回调为主,概念指数跌落4.18%,鼎捷软件和赛意信息均跌超10%。板块中,仅有华中数控、*ST日海和美的集团3股上涨,其间华中数控涨4.27%。
军工职业逆市上涨
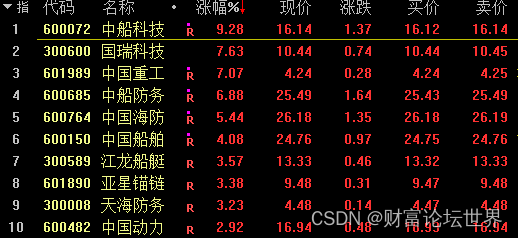
4月21日,军工股逆市上涨,职业指数盘中一度涨接近2.5%,午间收盘涨0.81%,全职业指数涨幅最高。其间,中船科技盘中涨停,午间收盘涨9.28%,理工导航涨13.5%,华如科技涨11.68%,另外中国卫通、中国重工和国瑞科技均涨超7%。
3月以来,军工职业震荡回调,职业指数一度跌落超8%,商场情绪较为悲观,板块估值处于低位。计算显示,到昨日收盘,约四分之一军工股达到年内最低翻滚市盈率。
组织看好军工板块估值修正前景。东北证券以为,随着“十四五”期间装备放量以及军演强度提升,军品的消耗进一步加快,在全军加快武器装备现代化建设的大背景下,军工工业链需求继续增加,板块有望继续获益,职业需求增加加快职业景气度继续兑现,进一步带动板块估值修正。
中信建投证券以为,虽然2022年有不利因素影响,军工职业仍保持了较高水平的业绩增加。随着“十四五”规划进入后半阶段,军工职业或许迎来新一轮景气周期。
16只军工股一季度业绩预喜
A股中,22家军工职业上市公司发布一季度业绩预告或定期陈述,以预告净利润同比增幅下限来看,16家预喜。
星网宇达一季度归母净利润1700万元至2000万元,同比扭亏为盈。2023年一季度,随着商场需求的增加以及项目检验康复正常,公司的经营收入及利润同步增加。
安达维尔一季度归母净利润50万元至100万元,同比扭亏为盈。公司称,民航事务方面,航班数量正逐渐康复到2019年同期水平,民航维修事务收入同比完成增加,厨房插件系列产品的科研及取证作业发展顺畅。防务事务方面,重大项目采办流程发展顺畅,机载设备相关项目的落地促进了事务的放量。同时,陈述期内,公司全面展开了智能及软件事务的商场开拓作业。
相关文章:

辉煌优配|军工板块逆市上涨,16只概念股已披露一季度业绩预喜
今日,军工股逆市上涨。 4月21日,A股三大股指低开低走,半导体、AI使用、信创工业、软件等科技属性概念领跌,国防军工、食品饮料和电力设备等板块上涨。 工业互联网中心工业规模超1.2万亿元 据央视新闻报道,本年是《工业…...
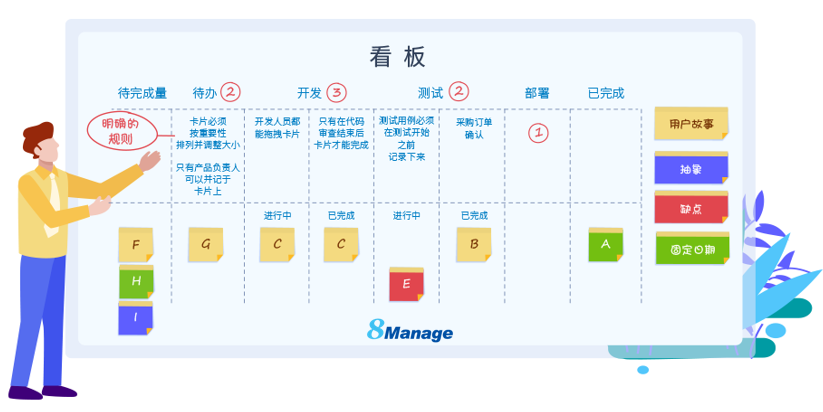
看板与 Scrum:有什么区别?
看板和Scrum是项目管理方法论,以小增量完成项目任务并强调持续改进。但是他们用来实现这些目标的过程是不同的。看板以可视化任务和连续流程为中心,而Scrum更多是关于为每个交付周期实施时间表和分配设定角色。 在看板和Scrum之间做出选择并不总是必要…...

零代码是什么?零代码平台适合谁用?
随着信息技术的发展,软件开发领域也不断发生变革,零代码(No-Code)开发模式越来越受到关注。 零代码到底是什么,能不能用通俗的话来说?这就来给大家讲一讲! 01 零代码为什么出现? 随…...

CNStack 云服务云组件:打造丰富的云原生技术中台生态
作者:刘裕惺 CNStack 相关阅读: CNStack 多集群服务:基于OCM 打造完善的集群管理能力 CNStack 虚拟化服务:实现虚拟机和容器资源的共池管理 CNStack 云边协同平台:实现原生边缘竟能如此简单 01 前言 CNStack 2.0…...

#PythonPytorch 1.如何入门深度学习模型
我之前也写过一篇关于Keras的深度学习入门blog,#Python&Keras 1.如何从无到有在自己的数据集上实现深度学习模型(入门),里面也有介绍了一下一点点机器学习的概念和理解深度学习的输入,如果对这方面有疑惑的朋友可以…...
)
[API]节点流和处理流字节流和字符流(七)
java将流分为节点流和处理流两类: 节点流:也称为低级流,是真实连接程序和另一端的"管道",负责实际读写数据的流,读写一定是建立在节点流的基础之上进行的。节点流好比家里的"自来水管",…...

开心档之C++ 模板
C 模板 目录 C 模板 函数模板 实例 类模板 实例 模板是泛型编程的基础,泛型编程即以一种独立于任何特定类型的方式编写代码。 模板是创建泛型类或函数的蓝图或公式。库容器,比如迭代器和算法,都是泛型编程的例子,它们都使用…...

拥抱还是革命,ChatGPT时代 AI专家给出15条科研生存之道
来源:专知 微信号:Quan_Zhuanzhi 你是学术机构的人工智能研究员吗?你是否担心自己无法应对当前人工智能的发展步伐?您是否觉得您没有(或非常有限)访问人工智能研究突破所需的计算和人力资源?你并不孤单; 我们有同样的感觉。越来越多的人工智能学者不…...
)
python算法中的数学算法(详解下)
目录 一. 学习目标: 二. 学习内容: Ⅰ. 数值优化 ①、均值 ②、方差 ③、协方差...
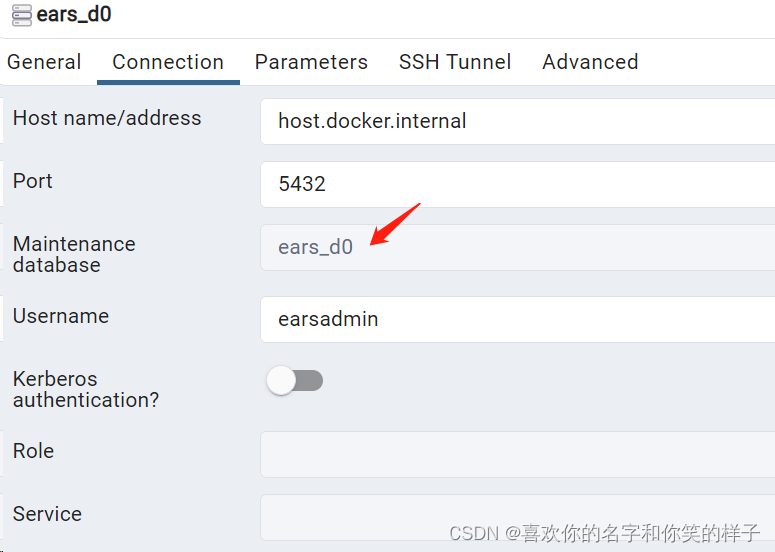
Docker Desktop使用PostgreSql配合PGAdmin的使用
在看此教程之前,请先下载安装Docker Desktop 安装成功可以查看版本 然后拉取postgresql的镜像:docker pull postgres:14.2 版本可以网上找一个版本,我的不是最新的 发现会报一个问题 no matching manifest for windows/amd64 10.0.19045 i…...
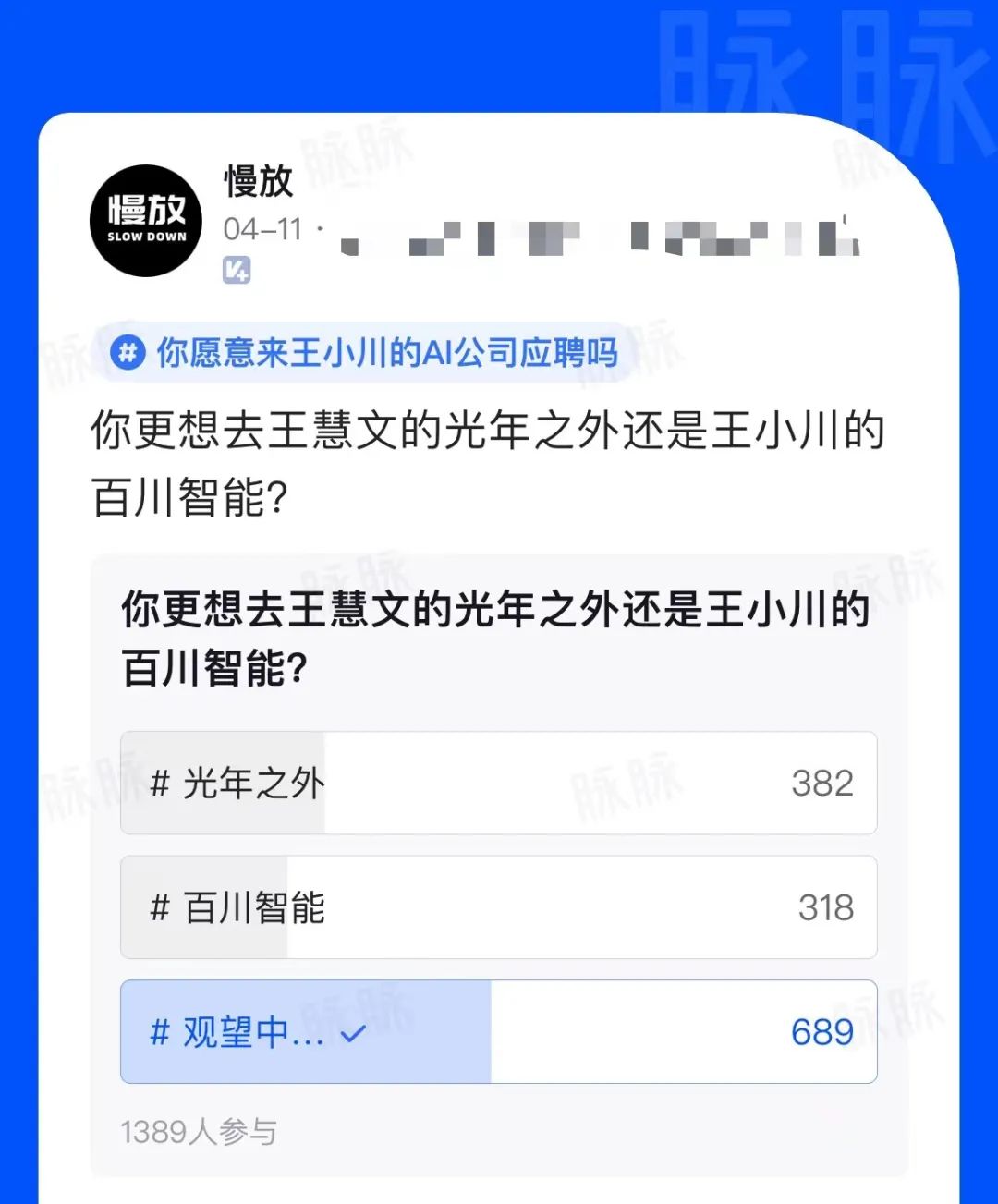
大佬入局AI,职场人有新机会了?
卸任搜狗CEO一年半后,王小川宣布在AI大模型领域创业,与前搜狗COO茹立云联合成立人工智能公司百川智能,打造中国版的OpenAI,并对媒体表示:“追上ChatGPT水平,我觉得今年内可能就能够实现,但对于G…...
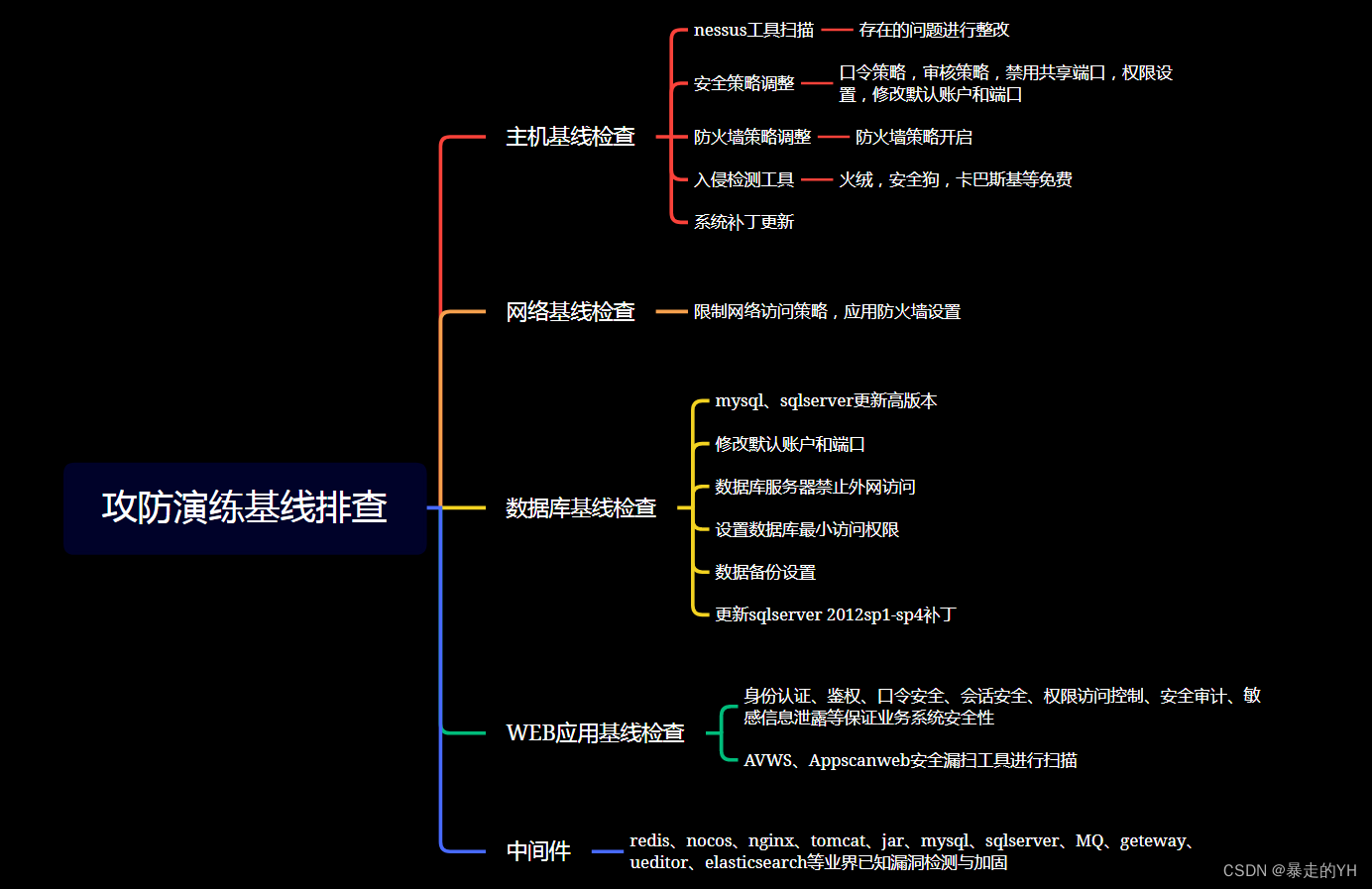
《攻防演练》在没有基础安全能力的情况下如何做好蓝队防守
目的: 1、净化企业或机构的网络环境、强化网络安全意识; 2、防攻击、防破坏、防泄密、防重大网络安全故障; 3、检验企业关键基础设施的安全防护能力; 4、提升关键基础设施的网络安全防范能力和水平。 现状: 那么问…...
疑难排查)
SLAM 十四讲(第一版)疑难排查
SLAM 十四讲(第一版)疑难排查 记录《SLAM 十四讲(第一版)》学习过程遇到的疑难杂症和排查结果,包括数学上的和编程环境上的,欢迎补充。 0. 使用软件环境 WSL:windows 下的 linux 子系统&…...
JavaScript的基础语法学习
文章目录 一、JavaScript let 和 const二、JavaScript JSON三、javascript:void(0) 含义四、JavaScript 异步编程总结 一、JavaScript let 和 const let 声明的变量只在 let 命令所在的代码块内有效。 const 声明一个只读的常量,一旦声明,常量的值就不…...

大语言模型Prompt工程之使用GPT4生成图数据库Cypher
大语言模型Prompt工程之使用GPT4生成图数据库Cypher 大语言模型Prompt工程之使用GPT4生成图数据库Cypher Here’s the table of contents: 大语言模型Prompt工程之使用GPT4生成图数据库Cypher 使用GPT4测试了生成Cypher的能力,没想到大型语言模型(LLM,La…...

ChatGPT已死?AutoGPT太强?
今天聊聊 AutoGPT。 OpenAI 的 Andrej Karpathy 都大力宣传,认为 AutoGPT 是 prompt 工程的下一个前沿。 近日,AI 界貌似出现了一种新的趋势:自主人工智能。 这不是空穴来风,最近一个名为 AutoGPT 的研究开始走进大众视野。特斯拉…...
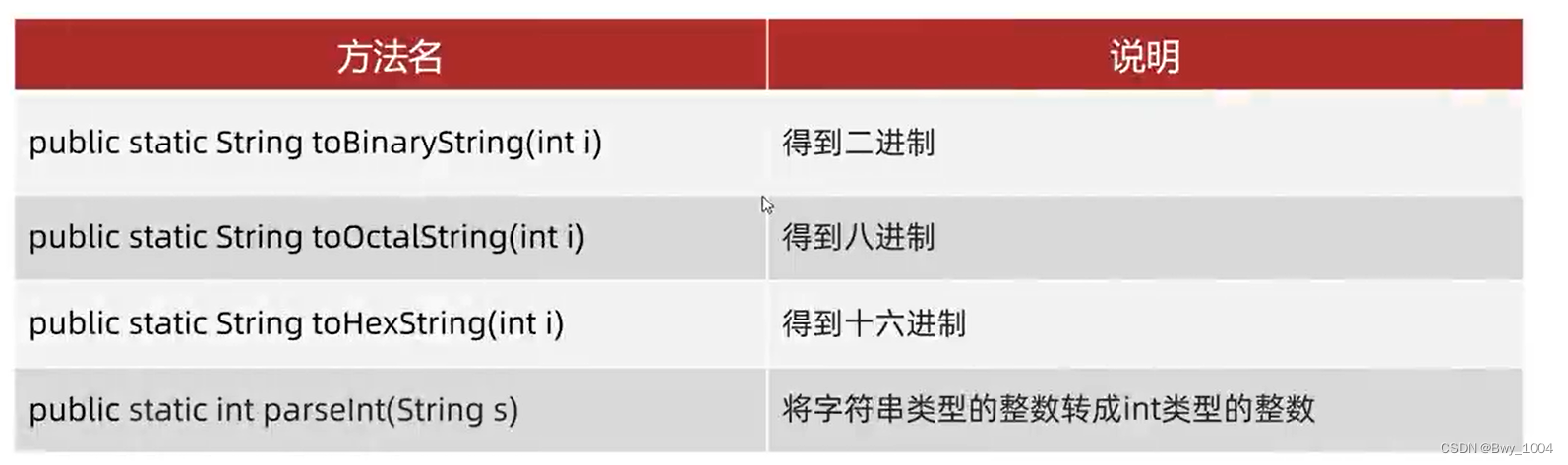
Java基础总结(二)
文章目录 一、ObjectObject中的成员方法(11个)toStringequalsclone 二、Objects三、BigInteger和BigDecimaBigIntegerBigDecima 四、正则表达式五、DateJDK7前时间相关类SimpleDateFormat类Calendar类 JDK8新增时间相关类 六、包装类异常 一、Object 没…...

大数据-玩转数据-oracle创建dblink及应用
一、创建DBLINK的应用场景 oracle在进行跨库访问时,可以通过创建dblink实现。 二、创建DBLINK应用场景 在tnsnames.ora中配置两个数据库别名:orcl(用户名:wangyong 密码:1988)、orcl2(用户名:wangyong 密码…...
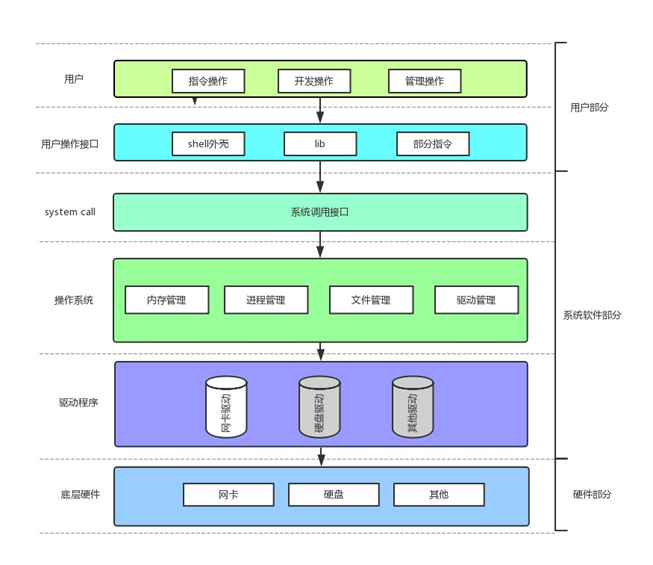
冯诺依曼体系结构
冯诺依曼体系结构 目录 冯诺依曼体系结构引入1、冯诺依曼体系结构1.1 内存1.2 操作系统预加载 2、操作系统2.1 理解管理2.2 系统调用接口2.3 操作系统四大基本功能 引入 冯诺依曼体系结构(von Neumann architecture)是现代计算机体系结构的基础…...

Axios请求(对ajax的二次封装)——Axios API、Axios实例、请求配置、Axios响应结构
axios起步——介绍和使用基本用例post请求 场景复现核心干货axios APIaxios(config)axios(url[,config])请求方式别名 axios实例创建一个axios实例axios.create([config])实例方法 axios请求配置axios响应结构 场景复现 最近学习与前端相关的小程序时,接触了异步请…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
