编译原理个人作业--第四章
构造FIRST和FOLLOW的大白话网站
第四章
1
考虑文法 G 1 G_1 G1:
S → a ∣ ∧ ∣ ( T ) T → T , S ∣ S S \rightarrow a|\land|(T) \\ T\rightarrow T,S|S S→a∣∧∣(T)T→T,S∣S
先复习左递归如何消除 原书p69页
- 类似于 P → P a ∣ b P\rightarrow Pa|b P→Pa∣b的形式,可以改写成
- P → b P ′ P\rightarrow bP^{'} P→bP′
- P ′ → a P ′ ∣ ϵ P^{'}\rightarrow aP^{'}|\epsilon P′→aP′∣ϵ
- 提公因子 P → P a 1 ∣ . . . ∣ P a m ∣ b 1 ∣ . . . b n ∣ P\rightarrow Pa_1|...|Pa_m|b_1|...b_n| P→Pa1∣...∣Pam∣b1∣...bn∣ 转换为
- P → b 1 P ′ ∣ . . . ∣ b n P ′ ∣ P\rightarrow b_1P^{'}|...|b_nP^{'}| P→b1P′∣...∣bnP′∣
- P ′ → a 1 P ′ ∣ . . . ∣ a m P ′ ∣ ϵ P^{'}\rightarrow a_1P^{'}|...|a_mP^{'}|\epsilon P′→a1P′∣...∣amP′∣ϵ
(1) 消除 G 1 G_1 G1左递归。并对每个非终结符,写出不带回溯的递归子程序
1. 消除左递归
分析:不难发现,左递归只在第二条地推中出现,应修改第二条
- 将b后面塞上一个新非终结符,删去原有的左递归部分
- 新非终结符可以递推出
左递归右半部分 + 新非终结符
S → a ∣ ∧ ∣ ( T ) T → S A A → , S A ∣ ϵ S \rightarrow a|\land|(T) \\ T\rightarrow SA\\ A\rightarrow ,SA|\epsilon S→a∣∧∣(T)T→SAA→,SA∣ϵ
2.递归下降子程序
详见原书 p74
procedure S;
beginif (sym = 'a') or (sym = '^')then advancce;else if sym = '('then beginadvance; Tif sym = ')'then advanceelse errorendelse error;
endprocedure T;
beginS;A
endprocedure A;
beginif sym = ','then beginadvance;S;Aendelse error
end
根据74页的定义
advance : 输入串指示器IP 指向下一个输入符号
sym : IP当前所指的输入符号
error : 出错程序
根据原文
(2) 改写后的文法是否为LL(1)的,给出预测分析表
知识点
证明文法为LL(1)
预测分析表 M 不含多重定义入口 ⇔ 文法为 L L ( 1 ) 预测分析表M不含多重定义入口 \Leftrightarrow 文法为LL(1) 预测分析表M不含多重定义入口⇔文法为LL(1)
构造分析表M算法
首先需要构造FISRT集
- 若 X ∈ V T X\in V_T X∈VT,则 F I R S T ( X ) = { X } FIRST(X) = \{X\} FIRST(X)={X}
- 若 X ∈ V N ∧ X → a . . . X\in V_N \land X\rightarrow a... X∈VN∧X→a..., 把a放入 F I R S T ( X ) FIRST(X) FIRST(X)中
- 若 X → ϵ X\rightarrow \epsilon X→ϵ, ϵ \epsilon ϵ也放入 F I R S T ( X ) FIRST(X) FIRST(X)中
- 若 X → Y . . . ∧ Y ∈ V N X\rightarrow Y... \land Y\in V_N X→Y...∧Y∈VN, 将 F I R S T ( Y ) − ϵ FIRST(Y) - \epsilon FIRST(Y)−ϵ 的元素加入 F I R S T ( X ) FIRST(X) FIRST(X)中
- 若 X → Y 1 Y 2 . . . Y k . . . ∧ Y 1 , . . . , Y i − 1 非终结符 ∧ 对于任何 j ( 1 ≤ j ≤ i − 1 ) , F I R S T ( Y j ) 含有 ϵ X\rightarrow Y_1Y_2...Y_k... \land Y_1,...,Y_{i-1}非终结符\land 对于任何j(1\le j \le i - 1), FIRST(Y_j)含有\epsilon X→Y1Y2...Yk...∧Y1,...,Yi−1非终结符∧对于任何j(1≤j≤i−1),FIRST(Yj)含有ϵ, 则把 F I R S T ( Y i ) − ϵ FIRST(Y_i)-\epsilon FIRST(Yi)−ϵ加入 F I R S T ( X ) 中 FIRST(X)中 FIRST(X)中
- 特别的,若所有的 F I R S T ( Y j ) 都含有 ϵ , j = 1 , 2 , . . . , k FIRST(Y_j)都含有\epsilon, j = 1,2,..., k FIRST(Yj)都含有ϵ,j=1,2,...,k, 把 ϵ \epsilon ϵ 加入 F I R S T ( X ) FIRST(X) FIRST(X)中
省流:在生成式右边,在最开头的终结符直接计入FIRST 然后开头的终结符除了epsilon也全计入, 如果右边整个串可以推导出空串,epsilon也计入
然后构造FOLLOW集
- 对于文法开始符号 S S S,放置
#到 F O L L O W ( S ) FOLLOW(S) FOLLOW(S) 中- 下面这个处理的是first,在B后面FIRST 放入 前一个非终结符的FOLLOW
- 若 A → α B β A\rightarrow \alpha B\beta A→αBβ, 把 F I R S T ( β ) − ϵ FIRST(\beta) - \epsilon FIRST(β)−ϵ 放入 F O L L O W ( B ) FOLLOW(B) FOLLOW(B)
- 后两种本质是同一种,将生成式左半部分的FOLLOW 给 末尾的非终结符FOLLOW
- A → α B A\rightarrow \alpha B A→αB, 把 F O L L O W ( A ) FOLLOW(A) FOLLOW(A)放入 F O L L O W ( B ) FOLLOW(B) FOLLOW(B)
- A → α B β ∧ β ⇒ ϵ A\rightarrow \alpha B\beta \land \beta \Rightarrow\epsilon A→αBβ∧β⇒ϵ (也就是说 ϵ ∈ F I R S T ( β ) \epsilon \in FIRST(\beta) ϵ∈FIRST(β)), 把 F O L L O W ( A ) FOLLOW(A) FOLLOW(A)放入 F O L L O W ( B ) FOLLOW(B) FOLLOW(B)
最后构造M
- 对文法 G G G 产生式 A → α A\rightarrow \alpha A→α 进行(2)(3)操作
- 终结符 a ∈ F I R S T ( α ) a\in FIRST(\alpha) a∈FIRST(α) 加入 M [ A , a ] M[A, a] M[A,a]中
- 若 ϵ ∈ F I R S T ( α ) \epsilon \in FIRST(\alpha) ϵ∈FIRST(α),则对任何 b ∈ F O L L O W ( A ) b \in FOLLOW(A) b∈FOLLOW(A),把 A → α A\rightarrow \alpha A→α 放入 M [ A , b ] M[A, b] M[A,b]中
- 没有定义则出错
解题过程
① 构造FIRST
首先考虑
S → a ∣ ∧ ∣ ( T ) S \rightarrow a|\land|(T) S→a∣∧∣(T)
不难发现,a,^,(都出现在了产生式右端的最左端,
所以有
F I R S T ( S ) = { a , ∧ , ( } FIRST(S) = \{a,\land, (\} FIRST(S)={a,∧,(}
考虑
T → S A T\rightarrow SA T→SA
根据构造FOLLOW集的第四种情况,需要将 F I R S T ( S ) − ϵ 所有元素放入 F I R S T ( T ) 中 FIRST(S) - \epsilon所有元素放入 FIRST(T)中 FIRST(S)−ϵ所有元素放入FIRST(T)中
F I R S T ( T ) = { a , ∧ , ( } FIRST(T) = \{a,\land, (\} FIRST(T)={a,∧,(}
考虑
A → , S A ∣ ϵ A\rightarrow ,SA|\epsilon A→,SA∣ϵ
F I R S T ( A ) = { , , ϵ } FIRST(A) = \{, , \epsilon\} FIRST(A)={,,ϵ}
② 构造FOLLOW
我们已经有了
F I R S T ( S ) = { a , ∧ , ( } FIRST(S) = \{a,\land, (\} FIRST(S)={a,∧,(}
F I R S T ( T ) = { a , ∧ , ( } FIRST(T) = \{a,\land, (\} FIRST(T)={a,∧,(}
F I R S T ( A ) = { , , ϵ } FIRST(A) = \{, , \epsilon\} FIRST(A)={,,ϵ}
首先考虑
S → a ∣ ∧ ∣ ( T ) S \rightarrow a|\land|(T) S→a∣∧∣(T)
- 根据规则1,需要存
#进 F O L L O W ( S ) FOLLOW(S) FOLLOW(S) - 根据规则2,需要将 F I R S T ( ) ) − ϵ FIRST())-\epsilon FIRST())−ϵ的元素放进去 F O L L O W ( T ) FOLLOW(T) FOLLOW(T)
于是第一步我们有
F O L L O W ( S ) = { # } F O L L O W ( T ) = { ) } FOLLOW(S) = \{\#\}\\ FOLLOW(T) = \{)\} FOLLOW(S)={#}FOLLOW(T)={)}
考虑
T → S A T\rightarrow SA T→SA
- 根据规则3,需要将 F O L L O W ( T ) FOLLOW(T) FOLLOW(T)的元素放进去 F O L L O W ( A ) FOLLOW(A) FOLLOW(A)
得到
F O L L O W ( S ) = { # } F O L L O W ( T ) = { ) } F O L L O W ( A ) = { ) } FOLLOW(S) = \{\#\}\\ FOLLOW(T) = \{)\}\\ FOLLOW(A) = \{)\} FOLLOW(S)={#}FOLLOW(T)={)}FOLLOW(A)={)}
考虑
A → , S A ∣ ϵ A\rightarrow ,SA|\epsilon A→,SA∣ϵ
- 根据规则2,需要将 F I R S T ( A ) − ϵ FIRST(A) - \epsilon FIRST(A)−ϵ的元素放进去 F O L L O W ( S ) FOLLOW(S) FOLLOW(S)
- 根据规则4(A可以推导出 ϵ \epsilon ϵ),需要将 F O L L O W ( A ) FOLLOW(A) FOLLOW(A)的元素放进去 F O L L O W ( S ) FOLLOW(S) FOLLOW(S)
得到
F O L L O W ( S ) = { , , ) , # } F O L L O W ( T ) = { ) } F O L L O W ( A ) = { ) } FOLLOW(S) = \{,, ),\#\}\\ FOLLOW(T) = \{)\}\\ FOLLOW(A) = \{)\} FOLLOW(S)={,,),#}FOLLOW(T)={)}FOLLOW(A)={)}
③ 构造M
S → a ∣ ∧ ∣ ( T ) T → S A A → , S A ∣ ϵ S \rightarrow a|\land|(T) \\ T\rightarrow SA\\ A\rightarrow ,SA|\epsilon S→a∣∧∣(T)T→SAA→,SA∣ϵ
F I R S T ( S ) = { a , ∧ , ( } F I R S T ( T ) = { a , ∧ , ( } F I R S T ( A ) = { , , ϵ } F O L L O W ( S ) = { , , ) , # } F O L L O W ( T ) = { ) } F O L L O W ( A ) = { ) } FIRST(S) = \{a,\land, (\}\quad FIRST(T) = \{a,\land, (\} \quad FIRST(A) = \{, , \epsilon\} \\ FOLLOW(S) = \{,, ),\#\}\quad FOLLOW(T) = \{)\}\quad FOLLOW(A) = \{)\} FIRST(S)={a,∧,(}FIRST(T)={a,∧,(}FIRST(A)={,,ϵ}FOLLOW(S)={,,),#}FOLLOW(T)={)}FOLLOW(A)={)}
对这三个生成式套用步骤2
首先按照 F I R S T ( S ) FIRST(S) FIRST(S) 我们有
| a a a | ∧ \land ∧ | ( ( ( | ) ) ) | , , , | # \# # | |
|---|---|---|---|---|---|---|
| S S S | S → a S\rightarrow a S→a | S → ∧ S\rightarrow \land S→∧ | S → ( T ) S\rightarrow (T) S→(T) |
然后按照 F I R S T ( T ) FIRST(T) FIRST(T) 我们有
| a a a | ∧ \land ∧ | ( ( ( | ) ) ) | , , , | # \# # | |
|---|---|---|---|---|---|---|
| S S S | S → a S\rightarrow a S→a | S → ∧ S\rightarrow \land S→∧ | S → ( T ) S\rightarrow (T) S→(T) | |||
| T T T | T → S A T\rightarrow SA T→SA | T → S A T\rightarrow SA T→SA | T → S A T\rightarrow SA T→SA |
根据 F I R S T ( A ) FIRST(A) FIRST(A)
| a a a | ∧ \land ∧ | ( ( ( | ) ) ) | , , , | # \# # | |
|---|---|---|---|---|---|---|
| S S S | S → a S\rightarrow a S→a | S → ∧ S\rightarrow \land S→∧ | S → ( T ) S\rightarrow (T) S→(T) | |||
| T T T | T → S A T\rightarrow SA T→SA | T → S A T\rightarrow SA T→SA | T → S A T\rightarrow SA T→SA | |||
| A A A | A → ϵ A\rightarrow \epsilon A→ϵ | A → , S A A\rightarrow ,SA A→,SA |
对这三个生成式套用步骤3,发现满足步骤3的只有 A → ϵ A\rightarrow \epsilon A→ϵ ( A → , S A A\rightarrow ,SA A→,SA这个生成式中, , S A ,SA ,SA无法变成 ϵ \epsilon ϵ)
- ϵ ∈ F I R S T ( A ) \epsilon \in FIRST(A) ϵ∈FIRST(A),对 ∀ b ∈ F O L L O W ( A ) \forall b\in FOLLOW(A) ∀b∈FOLLOW(A)将 A → α A\rightarrow\alpha A→α 放入M[A,b]中
不难发现FOLLOW(A)只有右括号 }, 然后重复填入 A → ϵ A\rightarrow \epsilon A→ϵ
最终的M没有多重定义入口
所以满足LL(1)
2
考虑文法G:
E → T E ′ E ′ → + E ∣ ϵ T → F T ′ T ′ → T ∣ ϵ F → P F ′ F ′ → ∗ F ′ ∣ ϵ P → ( E ) ∣ a ∣ b ∣ ∧ E\rightarrow TE^{'}\\E^{'}\rightarrow +E|\epsilon\\T\rightarrow FT^{'}\\ T^{'}\rightarrow T|\epsilon\\F\rightarrow PF^{'}\\F^{'}\rightarrow *F^{'}|\epsilon\\P\rightarrow (E)|a|b|\land E→TE′E′→+E∣ϵT→FT′T′→T∣ϵF→PF′F′→∗F′∣ϵP→(E)∣a∣b∣∧
(1) 计算文法G非终结符的FIRST和FOLLOW
计算FIRST
① 首先根据规则1: 若右边第一个符号是终结符或 ε ,则直接将其加入 FIRST(X)构造出最初始的FIRST
F I R S T ( E ) F I R S T ( E ′ ) = { + , ϵ } F I R S T ( T ) F I R S T ( T ′ ) = { ϵ } F I R S T ( F ) F I R S T ( F ′ ) = { ∗ , ϵ } F I R S T ( P ) = { ( , a , b , ∧ } FIRST(E)\quad FIRST(E^{'}) = \{+,\epsilon\} \quad FIRST(T) \quad FIRST(T^{'}) = \{\epsilon\} \\ FIRST(F) \quad FIRST(F^{'}) = \{*,\epsilon\} \quad FIRST(P) = \{ (, a, b, \land \} FIRST(E)FIRST(E′)={+,ϵ}FIRST(T)FIRST(T′)={ϵ}FIRST(F)FIRST(F′)={∗,ϵ}FIRST(P)={(,a,b,∧}
② 考虑规则2,右边第一个符号是非终结符,则将其 FIRST 集的的非 ε 元素加入 FIRST(X)
F I R S T ( E ) = { ( , a , b , ∧ } F I R S T ( E ′ ) = { + , ϵ } F I R S T ( T ) = { ( , a , b , ∧ } F I R S T ( T ′ ) = { ( , a , b , ∧ , ϵ } F I R S T ( F ) = { ( , a , b , ∧ } F I R S T ( F ′ ) = { ∗ , ϵ } F I R S T ( P ) = { ( , a , b , ∧ } FIRST(E) = \{ (, a, b, \land \}\quad FIRST(E^{'}) = \{+,\epsilon\} \quad \\ FIRST(T) = \{ (, a, b, \land \} \quad FIRST(T^{'}) = \{(, a, b, \land, \epsilon\} \\ FIRST(F) = \{ (, a, b, \land \} \quad FIRST(F^{'}) = \{*,\epsilon\} \quad FIRST(P) = \{ (, a, b, \land \} FIRST(E)={(,a,b,∧}FIRST(E′)={+,ϵ}FIRST(T)={(,a,b,∧}FIRST(T′)={(,a,b,∧,ϵ}FIRST(F)={(,a,b,∧}FIRST(F′)={∗,ϵ}FIRST(P)={(,a,b,∧}
再次检查规则1,2,3发现无法再使任意一个FIRST集合产生变化,故构造FOLLOW集合
FOLLOW集
首先使用规则1 若A->aBb是一条规则,则把FIRST(b)中的非ε元素加到FOLLOW(B)中,其中#为终止符,默认放在起始符的FOLLOW集合中
$$FOLLOW(E) = {#,)}\quad
FOLLOW(E^{‘}) = {} \quad
FOLLOW(T) ={+} \quad
FOLLOW(T^{’}) = {} \
FOLLOW(F) = {(, a, b, \land} \quad
FOLLOW(F^{'}) = {} \quad
FOLLOW§ = { * }
$$
使用规则2 若A->aB或A->aBb是一条规则且b=>ε,则把FOLLOW(A)加到FOLLOW(B)中;
F O L L O W ( E ) = { # , ) } F O L L O W ( E ′ ) = { # , ) } F O L L O W ( T ) = { # , ) , + } F O L L O W ( T ′ ) = { # , ) , + } F O L L O W ( F ) = { ( , a , b , ∧ , # , ) , + } F O L L O W ( F ′ ) = { ( , a , b , ∧ , # , ) , + } F O L L O W ( P ) = { ( , a , b , ∧ , # , ) , + , ∗ } FOLLOW(E) = \{\#,)\}\quad FOLLOW(E^{'}) = \{\#,)\} \quad FOLLOW(T) =\{\#,),+\} \quad FOLLOW(T^{'}) = \{\#,),+\} \\ FOLLOW(F) = \{(, a, b, \land, \#,),+\} \quad FOLLOW(F^{'}) = \{(, a, b, \land, \#,),+\} \quad FOLLOW(P) = \{ (, a, b, \land, \#,),+, * \} FOLLOW(E)={#,)}FOLLOW(E′)={#,)}FOLLOW(T)={#,),+}FOLLOW(T′)={#,),+}FOLLOW(F)={(,a,b,∧,#,),+}FOLLOW(F′)={(,a,b,∧,#,),+}FOLLOW(P)={(,a,b,∧,#,),+,∗}
(2) 证明文法为LL(1)
除了直接构造矩阵M看是否有多重入口,还可以使用p73的证明
- 文法无左递归
- 对文法非终结符A产生的候选符集合两两不相交 对于 A → a 1 ∣ . . . ∣ a n F i r s t ( a i ) ∩ F i r s t ( a j ) = ∅ 对于A\rightarrow a_1|...|a_n\quad First(a_i)\cap First(a_j) = \empty 对于A→a1∣...∣anFirst(ai)∩First(aj)=∅
- 文法非终结符A,若他候选符集包含 ϵ \epsilon ϵ 则 F I R S T ( A ) ∩ F O L L O W ( A ) = ∅ FIRST(A)\cap FOLLOW(A) = \empty FIRST(A)∩FOLLOW(A)=∅
① 不难发现,该文法无左递归
② 有多个候选符的产生式为 第二,第四,第六,第七行
不难发现
注意,你要求的是一整个串,比如+E,就得求FIRST(+E),而 +E的首字符只有+
F I R S T ( + E ) = { + } ∩ F I R S T ( ϵ ) = ∅ F I R S T ( T ) = { ( , a , b , ∧ } ∩ F I R S T ( ϵ ) = ∅ F I R S T ( ∗ F ′ ) = { ∗ } ∩ F I R S T ( ϵ ) = ∅ F I R S T ( ( E ) ) = { ( } , 与 a , b , ∧ 构成的 F I R S T 集两两不相交 FIRST(+E) = \{+\} \cap FIRST(\epsilon) = \empty\\ FIRST(T) = \{ (, a, b, \land\}\cap FIRST(\epsilon) = \empty\\ FIRST(*F^{'}) = \{*\} \cap FIRST(\epsilon) = \empty \\ FIRST((E)) = \{ (\},与a,b,\land构成的FIRST集两两不相交 FIRST(+E)={+}∩FIRST(ϵ)=∅FIRST(T)={(,a,b,∧}∩FIRST(ϵ)=∅FIRST(∗F′)={∗}∩FIRST(ϵ)=∅FIRST((E))={(},与a,b,∧构成的FIRST集两两不相交
③
产生式含 ϵ \epsilon ϵ的为第二,第四,第六行。显然
F I R S T ( E ′ ) ∩ F O L L O W ( E ′ ) = ∅ F I R S T ( T ′ ) ∩ F O L L O W ( T ′ ) = ∅ F I R S T ( F ′ ) ∩ F O L L O W ( F ′ ) = ∅ FIRST(E^{'}) \cap FOLLOW (E^{'}) = \empty \\ FIRST(T^{'}) \cap FOLLOW (T^{'}) = \empty \\ FIRST(F^{'}) \cap FOLLOW (F^{'}) = \empty FIRST(E′)∩FOLLOW(E′)=∅FIRST(T′)∩FOLLOW(T′)=∅FIRST(F′)∩FOLLOW(F′)=∅
综上,其为LL(1)文法
(3) 构造它的预测分析表
构造M
- 对文法 G G G 产生式 A → α A\rightarrow \alpha A→α 进行(2)(3)操作
- 终结符 a ∈ F I R S T ( α ) a\in FIRST(\alpha) a∈FIRST(α) 加入 M [ A , a ] M[A, a] M[A,a]中
- 若 ϵ ∈ F I R S T ( α ) \epsilon \in FIRST(\alpha) ϵ∈FIRST(α),则对任何 b ∈ F O L L O W ( A ) b \in FOLLOW(A) b∈FOLLOW(A),把 A → α A\rightarrow \alpha A→α 放入 M [ A , b ] M[A, b] M[A,b]中
- 没有定义则出错
对 E → T E ′ E\rightarrow TE^{'} E→TE′ , 我们根据规则2
| + | * | ( | ) | a | b | ⋀ | # | |
|---|---|---|---|---|---|---|---|---|
| E | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ |
对 E ′ → + E ∣ ϵ E^{'}\rightarrow +E|\epsilon E′→+E∣ϵ , 我们根据规则2
| + | * | ( | ) | a | b | ⋀ | # | |
|---|---|---|---|---|---|---|---|---|
| E | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | ||||
| E’ | E ′ → + E E^{'}\rightarrow +E E′→+E |
根据规则3
| + | * | ( | ) | a | b | ⋀ | # | |
|---|---|---|---|---|---|---|---|---|
| E | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | ||||
| E’ | E ′ → + E E^{'}\rightarrow +E E′→+E | E ′ → ϵ E^{'}\rightarrow \epsilon E′→ϵ | E ′ → ϵ E^{'}\rightarrow \epsilon E′→ϵ |
最终得到如下分析表
| + | * | ( | ) | a | b | ⋀ | # | |
|---|---|---|---|---|---|---|---|---|
| E | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | E → T E ′ E\rightarrow TE^{'} E→TE′ | ||||
| E’ | E ′ → + E E^{'}\rightarrow +E E′→+E | E ′ → ϵ E^{'}\rightarrow \epsilon E′→ϵ | E ′ → ϵ E^{'}\rightarrow \epsilon E′→ϵ | |||||
| T | T → F T ′ T\rightarrow FT^{'} T→FT′ | T → F T ′ T\rightarrow FT^{'} T→FT′ | T → F T ′ T\rightarrow FT^{'} T→FT′ | T → F T ′ T\rightarrow FT^{'} T→FT′ | ||||
| T’ | T ′ → ϵ T^{'}\rightarrow \epsilon T′→ϵ | T ′ → T T^{'}\rightarrow T T′→T | T ′ → ϵ T^{'}\rightarrow \epsilon T′→ϵ | T ′ → T T^{'}\rightarrow T T′→T | T ′ → T T^{'}\rightarrow T T′→T | T ′ → T T^{'}\rightarrow T T′→T | T ′ → ϵ T^{'}\rightarrow \epsilon T′→ϵ | |
| F | F → P F ′ F\rightarrow PF^{'} F→PF′ | F → P F ′ F\rightarrow PF^{'} F→PF′ | F → P F ′ F\rightarrow PF^{'} F→PF′ | F → P F ′ F\rightarrow PF^{'} F→PF′ | ||||
| F’ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ∗ F ′ F^{'}\rightarrow *F^{'} F′→∗F′ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ | F ′ → ϵ F^{'}\rightarrow \epsilon F′→ϵ |
| P | P → ( E ) P\rightarrow (E) P→(E) | P → a P\rightarrow a P→a | P → b P\rightarrow b P→b | P → ∧ P\rightarrow \land P→∧ |
(4) 构造它的递归下降分析程序
procedure E:
beginif sym = '(' or sym = 'a'or sym = 'B'or sym = '^'then beginT;E’endelseerror
endprocedure E’:
beginif sym = '+'then beginadvance;Eendelse if sym <> ')' and sym <> '#'then error
endprocedure T:
beginif sym = '(' or sym = 'a'or sym = 'B'or sym = '^'then beginF;T’endelseerror
endprocedure T’:
beginif sym = '(' or sym = 'a'or sym = 'B'or sym = '^'then beginT;endelse if sym = '*'error
endprocedure F:
beginif sym = '(' or sym = 'a'or sym = 'B'or sym = '^'then beginP;F’endelseerror
endprocedure F’:
beginif sym = '*' then beginadvance;F’end
endprocedure P:
beginif sym = 'a'or sym = 'B'or sym = '^'then advanceelse if sym = '(' then beginadvance;E;if sym = ')'then advanceelseerrorendelseerror
end
3
下面文法中那些是LL(1)文法?
一个文法G的预测分析表M不含多重定义入口,当且仅当该文法为LL(1)的。什么时候没有多重入口?从M的构造入手
- 生成时左部如果相同的话,他们各自的右部FIRST两两不相交(不然会有多重入口
- 其次,右边若存在epsilon属于某一个FIRST——并且最多只有一个能生成epsilon串(不然根据条件①也是会重复的),需要保证左部的FOLLOW和其余的右部FIRST两两不相交
(要是不会写这个那直接构造M也是可以的,但是都能构造M了,上面这个其实也应该懂。
(1)
S → A B c A → a ∣ ϵ B → b ∣ ϵ S\rightarrow ABc\\ A\rightarrow a|\epsilon\\ B\rightarrow b|\epsilon\\ S→ABcA→a∣ϵB→b∣ϵ
① 不含左递归
② 显然第二第三行的候选终结首符集两两不相交
③ 由于第二第三行推导式右边含 ϵ \epsilon ϵ
先求出相关的FIRST和FOLLOW集合
F I R S T ( S ) = { a , b , c } F O L L O W ( S ) = { # } F I R S T ( A ) = { a , ϵ } F O L L O W ( A ) = { b , c } F I R S T ( B ) = { b , ϵ } F O L L O W ( B ) = { c } FIRST(S) = \{a,b,c\} \quad FOLLOW(S) =\{\# \}\\ FIRST(A) = \{a, \epsilon\}\quad FOLLOW(A) =\{b,c\}\\ FIRST(B) = \{b, \epsilon\}\quad FOLLOW(B) =\{c \}\\ FIRST(S)={a,b,c}FOLLOW(S)={#}FIRST(A)={a,ϵ}FOLLOW(A)={b,c}FIRST(B)={b,ϵ}FOLLOW(B)={c}
不难发现A,B对应的FIRST集与FOLLOW集合相交为空集
满足LL(1)
(2)
S → A b A → a ∣ B ∣ ϵ B → b ∣ ϵ S\rightarrow Ab\\ A\rightarrow a|B|\epsilon\\ B\rightarrow b|\epsilon S→AbA→a∣B∣ϵB→b∣ϵ
① 不含左递归
F I R S T ( S ) = { a , b } F O L L O W ( S ) = { # } F I R S T ( A ) = { a , b , ϵ } F O L L O W ( A ) = { b } F I R S T ( B ) = { b , ϵ } F O L L O W ( B ) = { b } FIRST(S) = \{a,b\} \quad FOLLOW(S) =\{\# \}\\ FIRST(A) = \{a, b,\epsilon\}\quad FOLLOW(A) =\{b\}\\ FIRST(B) = \{b, \epsilon\}\quad FOLLOW(B) =\{ b\}\\ FIRST(S)={a,b}FOLLOW(S)={#}FIRST(A)={a,b,ϵ}FOLLOW(A)={b}FIRST(B)={b,ϵ}FOLLOW(B)={b}
由于A->B,参考规则2(因为B后面没字符串了,为空船),需要将follow(A)传递给follow(B)
② 对于第二行导出式子,有 F I R S T ( B ) ∩ F I R S T ( ϵ ) = { ϵ } FIRST(B)\cap FIRST(\epsilon) = \{\epsilon\} FIRST(B)∩FIRST(ϵ)={ϵ}
不符合LL(1)
(3)
S → A B B A A → a ∣ ϵ B → b ∣ ϵ S\rightarrow ABBA\\ A\rightarrow a|\epsilon\\ B\rightarrow b|\epsilon S→ABBAA→a∣ϵB→b∣ϵ
① 不含左递归
F I R S T ( S ) = { a , b , ϵ } F O L L O W ( S ) = { # } F I R S T ( A ) = { a , ϵ } F O L L O W ( A ) = { b , # } F I R S T ( B ) = { a , b , ϵ } F O L L O W ( B ) = { a , b , # } FIRST(S) = \{a,b,\epsilon\} \quad FOLLOW(S) =\{\# \}\\ FIRST(A) = \{a,\epsilon\}\quad FOLLOW(A) =\{b,\#\}\\ FIRST(B) = \{a, b,\epsilon\}\quad FOLLOW(B) =\{a, b, \#\}\\ FIRST(S)={a,b,ϵ}FOLLOW(S)={#}FIRST(A)={a,ϵ}FOLLOW(A)={b,#}FIRST(B)={a,b,ϵ}FOLLOW(B)={a,b,#}
② 对于第二行和第三行,他们的候选终结首符集两两不相交
③: F I R S T ( B ) ∩ F O L L O W ( B ) = { a , b } ≠ ∅ FIRST(B)\cap FOLLOW(B) = \{a,b\} \neq \empty FIRST(B)∩FOLLOW(B)={a,b}=∅
不满足LL(1)
(4)
S → a S e ∣ B B → b B e ∣ C C → c C e ∣ d S\rightarrow aSe|B\\ B\rightarrow bBe|C\\ C\rightarrow cCe|d S→aSe∣BB→bBe∣CC→cCe∣d
① 不含左递归
F I R S T ( S ) = { a , b , c , d } F O L L O W ( S ) = { e , # } F I R S T ( B ) = { b , c , d } F O L L O W ( B ) = { e , # } F I R S T ( C ) = { c , d } F O L L O W ( C ) = { e , # } FIRST(S) = \{a,b,c,d\} \quad FOLLOW(S) =\{e,\#\}\\ FIRST(B) = \{b,c,d\}\quad FOLLOW(B) =\{e,\#\}\\ FIRST(C) = \{c,d\}\quad FOLLOW(C) =\{e,\#\}\\ FIRST(S)={a,b,c,d}FOLLOW(S)={e,#}FIRST(B)={b,c,d}FOLLOW(B)={e,#}FIRST(C)={c,d}FOLLOW(C)={e,#}
不难发现,均满足条件②和条件③
符合LL(1)文法
4
对下面的文法
E x p r → − E x p r E x p r → ( E x p r ) ∣ V a r E x p r T a i l E x p r T a i l → − E x p r ∣ ϵ V a r → i d V a r T a i l V a r T a i l → ( E x p r ) ∣ ϵ Expr\rightarrow -Expr\\ Expr \rightarrow (Expr)| Var\ ExprTail\\ ExprTail \rightarrow -Expr|\epsilon\\ Var\rightarrow id\ VarTail\\ VarTail \rightarrow (Expr)|\epsilon Expr→−ExprExpr→(Expr)∣Var ExprTailExprTail→−Expr∣ϵVar→id VarTailVarTail→(Expr)∣ϵ
构造LL(1)分析表
重命名一下,太花里胡哨了
E → − E E → ( E ) ∣ V D D → − E ∣ ϵ V → i d C C → ( E ) ∣ ϵ E\rightarrow -E\\ E \rightarrow (E)|\ VD\\ D \rightarrow -E|\epsilon\\ V\rightarrow id\ C\\ C \rightarrow (E)|\epsilon E→−EE→(E)∣ VDD→−E∣ϵV→id CC→(E)∣ϵ
构造FIRST和FOLLOW
F I R S T ( E ) = { − , ( , i d } F O L L O W ( E ) = { # , ) } F I R S T ( V ) = { i d } F O L L O W ( V ) = { − , # , ) } F I R S T ( D ) = { − , ϵ } F O L L O W ( D ) = { # , ) } F I R S T ( C ) = { ( , ϵ } F O L L O W ( C ) = { − , # , ) } FIRST(E) = \{-,(,id\} \quad FOLLOW(E) = \{\# ,)\}\\ FIRST(V) = \{id\} \quad FOLLOW(V) = \{-,\# ,)\}\\ FIRST(D) = \{-,\epsilon\} \quad FOLLOW(D) = \{\# ,)\}\\ FIRST(C) = \{(,\epsilon\} \quad FOLLOW(C) = \{-,\# ,)\}\\ FIRST(E)={−,(,id}FOLLOW(E)={#,)}FIRST(V)={id}FOLLOW(V)={−,#,)}FIRST(D)={−,ϵ}FOLLOW(D)={#,)}FIRST(C)={(,ϵ}FOLLOW(C)={−,#,)}
| - | id | ( | ) | # | |
|---|---|---|---|---|---|
| E | E → − E E\rightarrow -E E→−E | E → V D E\rightarrow VD E→VD | E → ( E ) E\rightarrow (E) E→(E) | ||
| D | D → − E D\rightarrow -E D→−E | D → ϵ D\rightarrow \epsilon D→ϵ | D → ϵ D\rightarrow \epsilon D→ϵ | ||
| V | V → i d C V\rightarrow id\ C V→id C | ||||
| C | C → ϵ C\rightarrow \epsilon C→ϵ | C → ( E ) C\rightarrow (E) C→(E) | C → ϵ C\rightarrow \epsilon C→ϵ | C → ϵ C\rightarrow \epsilon C→ϵ |
给出句子 id--id((id))的分析过程
| 分析栈 | 输入 | 产生式 |
|---|---|---|
| #E | id–id((id)) # | |
| #DV | id–id((id)) # | E→VD |
| #DCid | id–id((id)) # | V→idC |
| #DC | –id((id)) # | |
| #D | –id((id)) # | C→ε |
| #E- | –id((id)) # | D→-E |
| #E | -id((id)) # | |
| #E- | -id((id)) # | E→-E |
| #E | id((id)) # | |
| #DV | id((id)) # | E→VD |
| #DCid | id((id)) # | V→idC |
| #DC | ((id)) # | |
| #D)E( | ((id)) # | C→(E) |
| #D)E | (id)) # | |
| #D))E( | (id)) # | E→(E) |
| #D))E | id)) # | |
| #D))DV | id)) # | E→VD |
| #D))DCid | id)) # | V→idC |
| #D))DC | )) # | |
| #D))D | )) # | C→ϵ |
| #D)) | )) # | D→ϵ |
| #D) | ) # | |
| #D | # | |
| # | # | D→ϵ |
ps:麻了,这作业花了我六七个小时
相关文章:

编译原理个人作业--第四章
构造FIRST和FOLLOW的大白话网站 第四章 1 考虑文法 G 1 G_1 G1: S → a ∣ ∧ ∣ ( T ) T → T , S ∣ S S \rightarrow a|\land|(T) \\ T\rightarrow T,S|S S→a∣∧∣(T)T→T,S∣S 先复习左递归如何消除 原书p69页 类似于 P → P a ∣ b P\rightarrow Pa|b P→Pa∣b的…...

学习笔记:数据库简介
数据库是一系列可以方便的访问和修改的数据的集合。 所有数据库管理系统的主要工作都是可靠的存储数据并使其对用户可用。 目前最常见的数据库模型主要是两种,即关系型数据库和非关系型数据库。 一、按数据的组织方式 数据从组织的角度上,主要分为结…...
day18_集合
今日内容 零、 复习昨日 一、集合框架体系 二、Collection 三、泛型 四、迭代 五、List 六、ArrayList 七、LinkedList 零、 复习昨日 晨考 一、集合框架体系 数组: 是一个容器,用来存放数据的 定长只能存储同一种数据类型的数据int[] 可以存储int值,Student[] 可以存储引用类型…...

Go面试必会基础题
文章目录 1.下面代码有什么错误?2.下面代码有什么问题?3.下面代码输出什么?4.下面这段代码输出什么? 1.下面代码有什么错误? func main() {one : 0one : 1 }参考答案及解析:变量重复声明。不能在单独的声…...
发送封包协议实现XXZ批量秒分解装备
通过发送封包,我们可以让一些反复的枯燥的行为变的简单,高效。 比如XXZ的萃取装备,我们可以一瞬间萃取大量的装备,而省去读条的过程。 我们来萃取一下看看效果 手动萃取是有读条的,那么如果很多装备的话,…...

Spring学习——Nginx
Nginx概述 Nginx介绍 Nginx是一款轻量级的web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器。其特点是占有内存少,并发能力强,事实上nginx的并发能力在同类型的网页服务器中表现较好,中国大陆使用nginx的网…...

记录 vue-cli 安装过程
1. VueCli CLI 是 Commond-Line Interface 的缩写 如果开发大型项目,肯定需要考虑代码目录结构、项目结构和部署、热加载、代码单元测试等事情,那么你必然需要使用 VueCLI,使用 VueCLI 可以快速搭建 vue 开发环境以及对应的 webpack 配置。 …...
含氢微网优化调度模型matlab
目录 1 主要内容 模型示意图 目标函数 2 部分程序 3 程序结果 4 下载链接 1 主要内容 最近咨询含氢微网优化调度模型的同学较多,本次就分享一个高质量的源码资源。该程序方法复现《Simulation of design and operation of hydrogen energy utilization syste…...

【springcloud开发教程】路由网关——zuul
官方资料:https://github.com/Netflix/zuul/ 什么是Zuul? Zuul包含了两个主要的功能:路由和过滤 路由功能将外部请求转发到具体的微服务实例上,是实现外部访问统一入口的基础,而过滤器功能则负责对请求的处理过程进行干预&#…...

DF竞赛平台携手嬴彻科技与清华大学智能产业研究院,助力自动驾驶挑战赛圆满落幕!
由DataFountain竞赛平台(简称DF平台)提供办赛支持的「首届“嬴彻-清华AIR杯”自动驾驶挑战赛:决策规划算法」已圆满落幕。作为一场前沿性自动驾驶类比赛,本次大赛立足“高速道路”和“城市道路”两大真实场景,选择“半…...
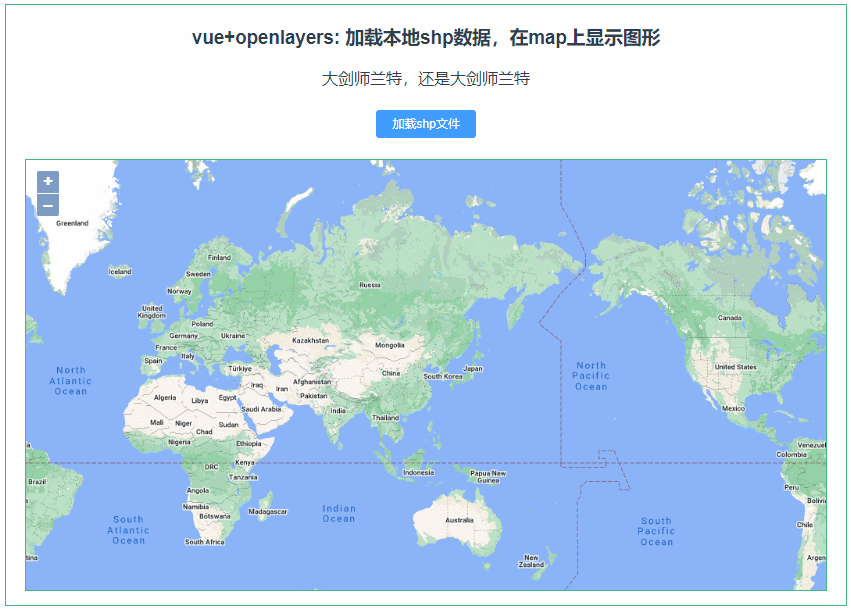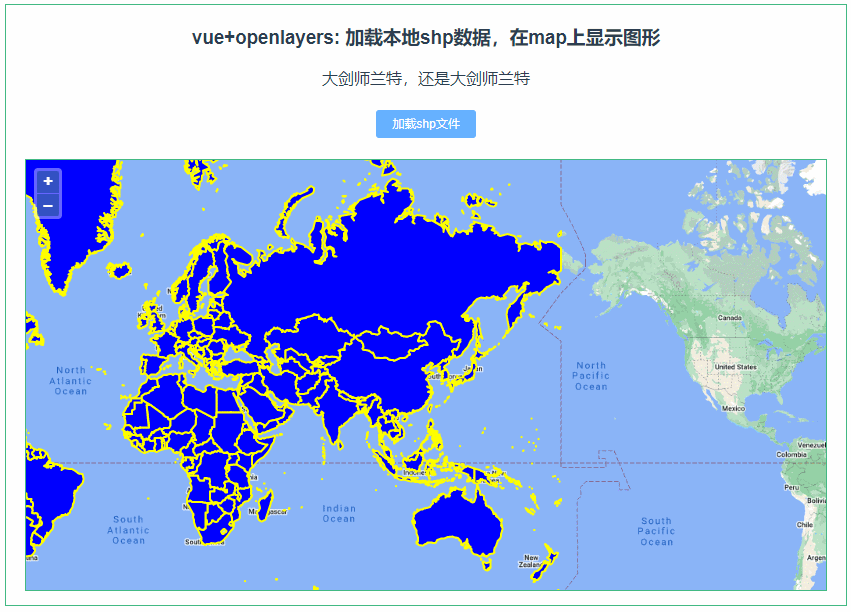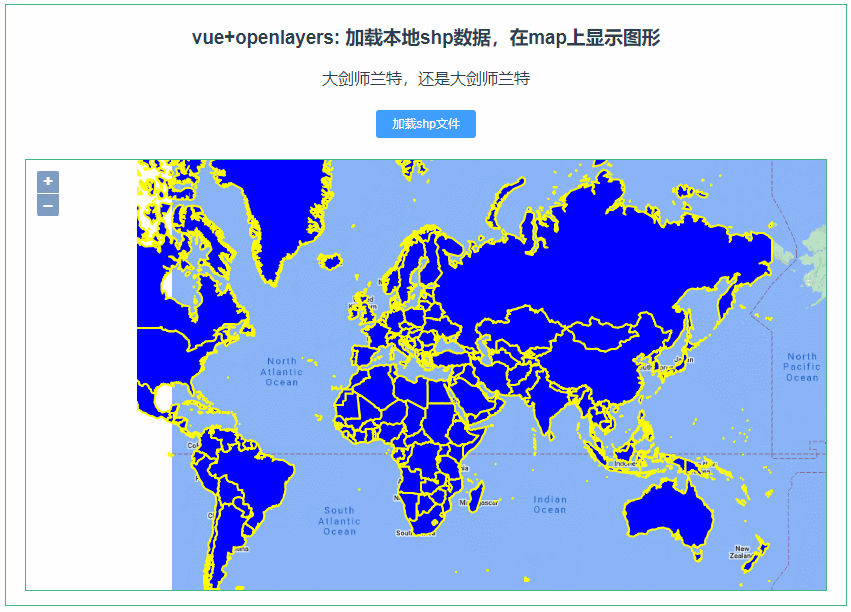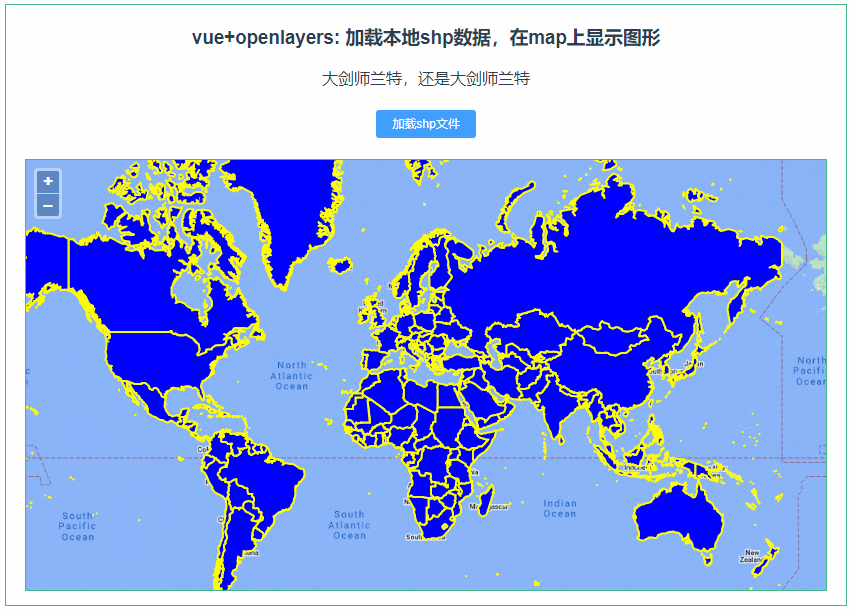
234:vue+openlayers 加载本地shp数据,在map上显示图形
第234个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+openlayers中利用shapefile读取本地的shp数据,并在地图上显示图形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果 文章目录 示例效果安装引用配置方式示例源代码(共143行)相关API参考:专栏…...
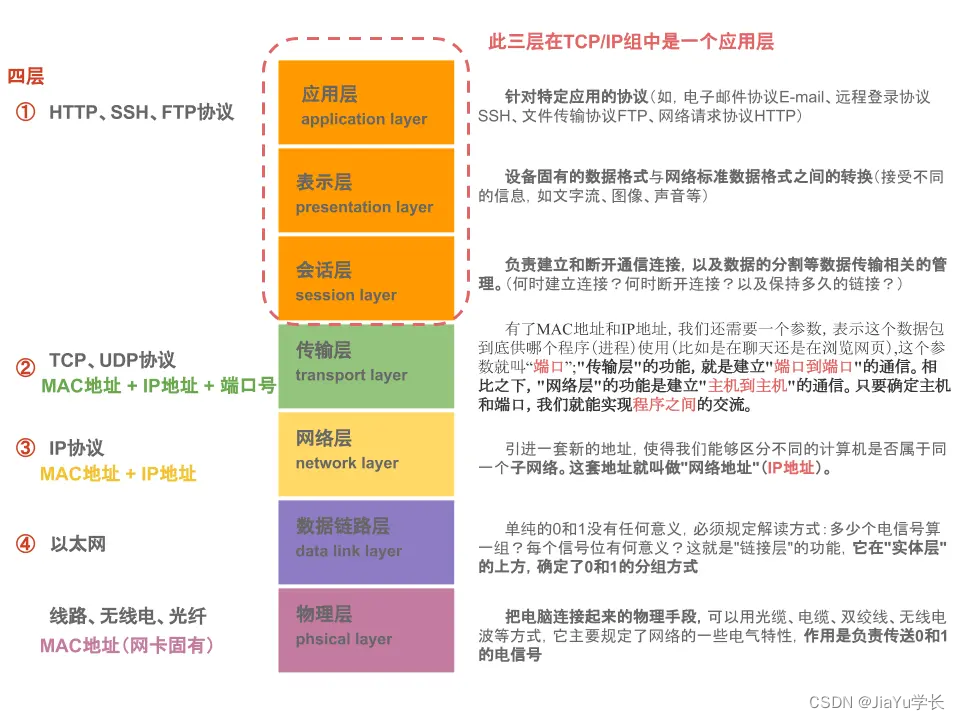
网络模型-网络体系结构(OSI、TCP/IP)
网络模型(网络体系结构) 网络模型网络的体系结构OSI模型TCP/IP模型OSI和TCP/IP模型对应关系图 常见网络协议 网络模型 网络的体系结构 1、网络采用分而治之的方法设计,将网络的功能划分为不同的模块,以分层的形式有机组合在一起…...

园区智慧导览地图软件,智慧工厂导航定位怎么解决方案的
智慧工厂导航定位怎么解决方案的地图新基建是行业的核心数字基础需求之一,行业内中已构建了较为完整的城市级地理信息系统。园区管理涉及众多方面,因此园区的智慧信息化建设至关重要,需求越来越广泛。在智慧园区中,基于园区的电子…...

Redis高可用之3种集群方案对比
Redis集群方案使用建议: Redis cluster:除非是1000个节点以上的超大规模集群,优先考虑使用Redis clustercodis:旧项目如果仍在使用codis,可继续使用,但也推荐迁移到Redis clustertwemproxy:不建…...

java 线程唤醒于阻塞的常用方法
1.分类描述 1.sleep() 休眠2.suspend() 暂停和 resume() 继续3.yield() 让步 就是我放弃本次执行,但继续排队,下一次有机会在执行。 4.wait() 和 notify() notifyAll() 注:这两个方法,属于Object类,而不属于Thread…...
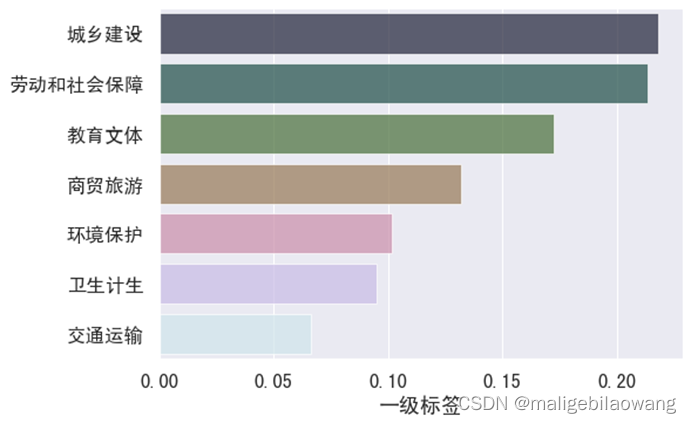
面包多面包多面包多面包多面包多面包多
1.背景 1.摘要 本文是针对智慧政务中的文本数据挖掘应用的研究。通过建立基于三层网络结构的fastText文本分类模型,聚类量化模型,熵权评估模型解决了群众留言分类,热点问题挖掘,答复意见评价等问题。 针对群众留言分类问题&#…...
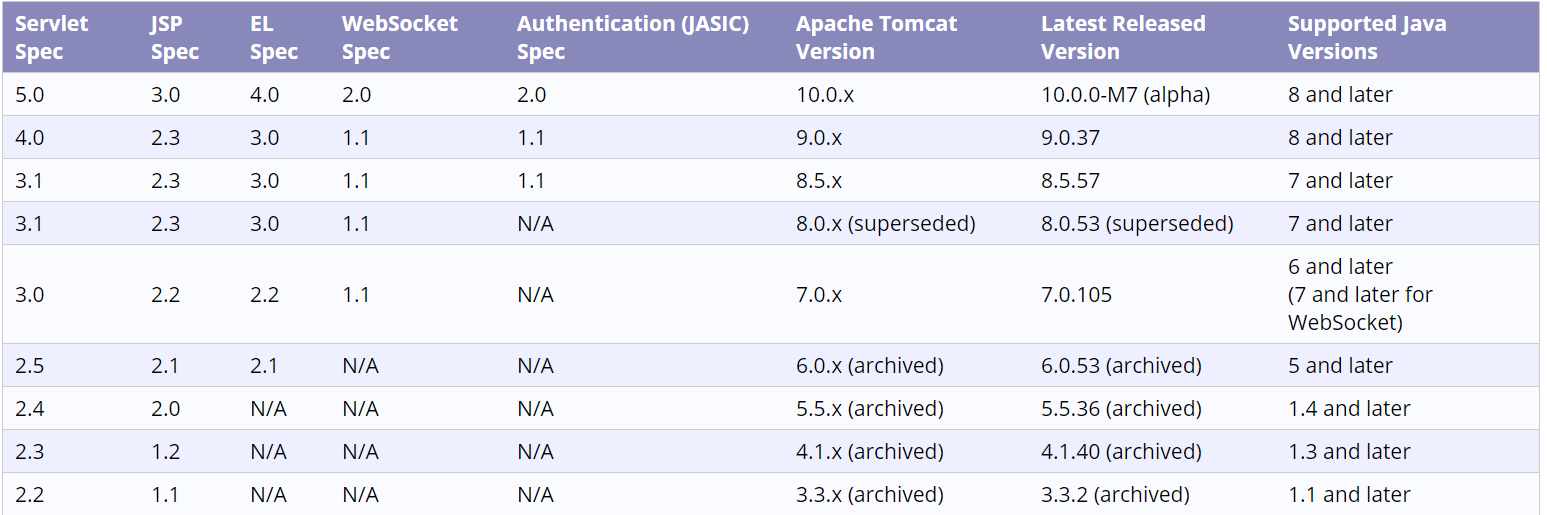
windows下Tomcat安装
目录 1.安装java环境 2.配置Tomcat环境变量 3.安装服务 4.启动前修改配置文件 (1)设置tomcat端口 (2)设置临时日志等文件夹的位置 5.放入应用 6.启动Tomcat服务 1.安装java环境 安装tomcat版本对应的JDK 比如:…...
4月17号软件资讯更新合集.....
CrateDB 5.3.0 发布,分布式 SQL 数据库 CrateDB 是一个分布式的 SQL 数据库,使得实时存储和分析大量的机器数据变得简单。CrateDB 提供了通常与 NoSQL 数据库相关的可扩展性和灵活性,最小的 CrateDB 集群可以轻松地每秒摄取数万条记录。这些…...
[java基础]面向对象(五)
访问控制修饰符:--------------保护数据的安全(隐藏数据、暴露行为),实现封装 public:公开的,任何类 private:私有的,本类 protected:受保护的,本类、派生类、同包类 默认的&…...
React应用(基于React脚手架)
目录 前言:一、使用create-react-app创建react应用1、什么是 react 脚手架?2. 创建 cli 脚手架方式13. 创建 cli 脚手架方式24. npx:5. react脚手架项目结构6. 功能界面的组件化编码流程(通用)7. 如何更改脚手架版本 二、React 组…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

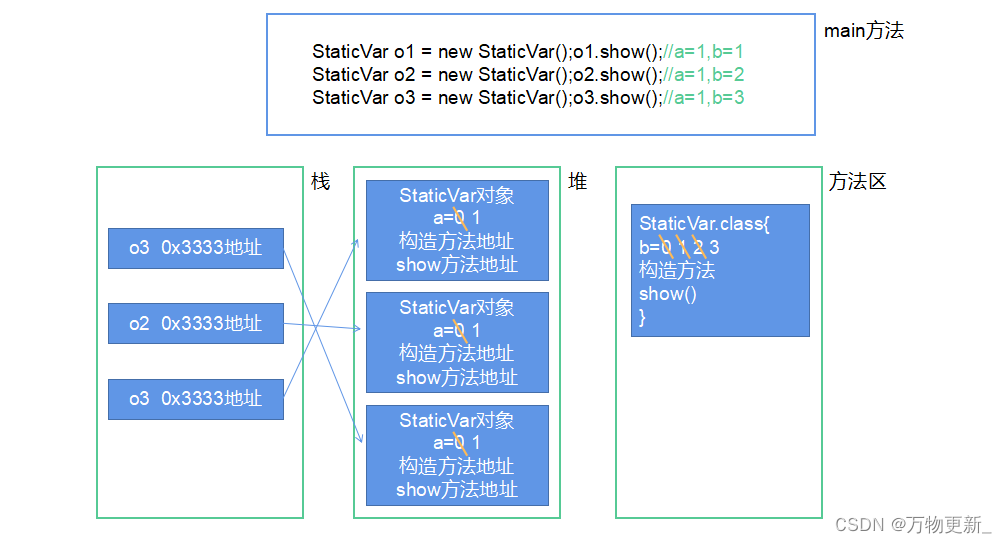
JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
