相量的加减乘除计算
相量的加减乘除计算
矢量是物理学中的术语,是指具有大小(magnitude)和方向的量。如速度、加速度、力等等就是这样的量。向量是数学中的术语,也称为欧几里得向量、几何向量、矢量。与向量对应的量叫做数量,在物理学中称为标量,数量只有大小,没有方向。
相量是电子工程学中用以表示正弦量大小和相位的矢量。它仅用来表示具有正弦波的电压和电流,将电压电流用一个复数形式表示,以方便计算。为了让这两个相量相乘具有功率的意义,在极坐标系中,使用电压和电流的有效值来表示相量的大小表示,相量的角度使用电压电流的初相角。不再象直角坐标系,采用幅值和正弦函数的乘积来表示。
由于电压和电流同频,我们将电压相量和电流相量画在同一个复平面中(极坐标系),称为相量图。
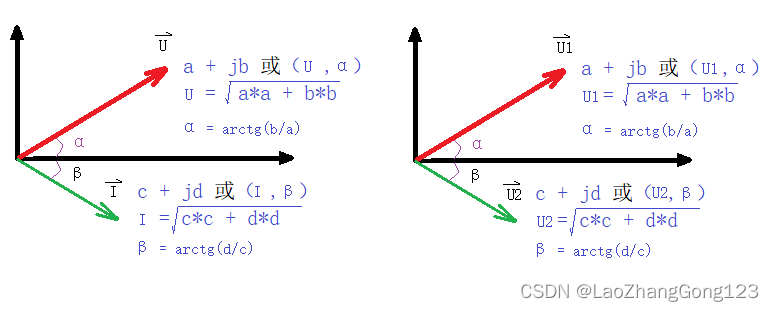
在上图中:
相量U = a + jb = U * [cos(α)+ jsin(α)]
相量I = c + jd = I * [cos(β)+ jsin(β)]
相量U1 = a + jb = U1 * [cos(α)+ jsin(α)]
相量U2 = c + jd = U2 * [cos(β)+ jsin(β)]
采用有效值表示相量的大小,是因为考虑到功率计算,如果继续使用幅值表示相量的大小,会导致电压电流相量的乘积就失去了功率的意义,因此,这里采用有效值表示相量的大小。采用初相角表示方向,是因为电压电流相量同频。
相量加法

相量U1 + 相量U2 = U1 * [cos(α)+ jsin(α)] + U2 * [cos(β)+ jsin(β)]
= [U1 * cos(α)+ U2 * cos(β)] + j[U1 * sin(α)+ U2 * sin(β)]
相量和模的平方:
[U1 * cos(α)+ U2 * cos(β)]* [U1 * cos(α)+ U2 * cos(β)]+ [U1 * sin(α)+ U2 * sin(β)]* [U1 * sin(α)+ U2 * sin(β)]
= U1*U1 + U2*U2 + 2U1*U2*[cos(α) cos(β) + sin(α) sin(β)]
=U1*U1 + U2*U2 + 2U1*U2*cos(α-β)
相量和的角度:
arctg{[U1 * sin(α)+ U2 * sin(β)] /[U1 * cos(α)+ U2 * cos(β)]}
相量加法结论:相量的实部和实部相加,虚部和虚部相加
相量减法
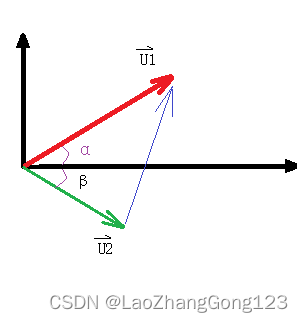
相量U1 - 相量U2 = U1 * [cos(α)+ jsin(α)] - U2 * [cos(β)+ jsin(β)]
= [U1 * cos(α)- U2 * cos(β)] + j[U1 * sin(α)- U2 * sin(β)]
相量和模的平方:
[U1 * cos(α)- U2 * cos(β)]* [U1 * cos(α)- U2 * cos(β)]+ [U1 * sin(α)- U2 * sin(β)]* [U1 * sin(α)- U2 * sin(β)]
= U1*U1 + U2*U2 - 2U1*U2*[cos(α) cos(β) + sin(α) sin(β)]
=U1*U1 + U2*U2 - 2U1*U2*cos(α-β)
相量和的角度:
arctg{[U1 * sin(α)- U2 * sin(β)] /[U1 * cos(α)- U2 * cos(β)]}
相量减法结论:相量的实部和实部相减,虚部和虚部相减
相量乘法
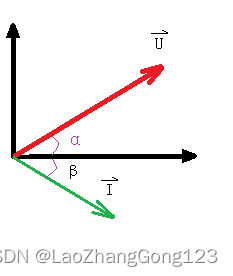
相量U和相量I的乘积=[U*cos(α)+jU*sin(α)] * [I*cos(β)+jI*sin(β)]
=UI{[cos(α)cos(β)-sin(α)sin(β)] + j [cos(α) sin(β)+sin(α) cos(β)]}
=UI[cos(α+β) + jsin(α+β)]
相量乘法结论:“积的模”等于相量的模相乘,“积的角度”等于相量的角度相加。
有功功率计算

有功功率功是“电流的有功分量”乘以“电压相量的模”,因此,有功功率为UIcos(α-β)。
相量除法
相量U和相量I的商=[U*cos(α)+jU*sin(α)] / [I*cos(β)+jI*sin(β)]
=(U/I)* [cos(α)+jsin(α)] / [cos(β)+jsin(β)]
=(U/I)* [cos(α)+jsin(α)] *[cos(β)-jsin(β)]/ {[cos(β)+jsin(β)]* [cos(β)-jsin(β)]}
=(U/I)* [cos(α)+jsin(α)] *[cos(β)-jsin(β)]
=(U/I)* [cos(α)cos(β)+ sin(α) sin(β)]+j[sin(α)cos(β)-cos(α)sin(β)]
=(U/I)* [cos(α-β)+jsin(α-β)]
相量除法结论:“商的模”等于相量的模相除,“商的角度”等于相量的角度相减。
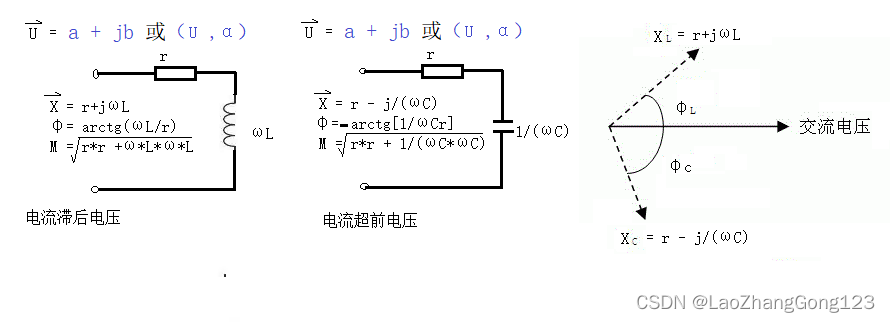
复阻抗的相位角φ,阻抗是复阻抗的模,容抗为1/ωC,感抗为ωL
电压相量为U[cos(α)+jsin(α)]
复阻抗是一个复数,为M[cos(φ)+jsin(φ)]
电流相量= U[cos(α)+jsin(α)] / M[cos(φ)+jsin(φ)]
=(U/M)* [cos(α)+jsin(α)] / [cos(φ)+jsin(φ)]
=(U/M)* [cos(α)+jsin(α)] * [cos(φ)-jsin(φ)]
=(U/M)*{[cos(α)cos(φ) + sin(α)sin(φ)]+j[sin(α)cos(φ)- cos(α)sin(φ) }
=(U/M)*{[cos(α-φ)]+j[sin(α-φ) }
电流初相角为 (α-φ),即电流初相角等于电压初相角与复阻抗角度的差。
因此,当φ> O时,电流初相角小于电压初相角,即电流滞后电压;当φ< O时,电流初相角大于电压初相角,即电流超前电压。
电压电流相位差ψ=α-(α-φ)= φ,即电压电流相位差等于复阻抗的角度值。
因此,功率因素等于阻抗角度的余弦值,等于电压电流相位差的余弦值。知道了功率因素,就等于告诉了复阻抗的角度值。
很多学习《电路分析》的人,不知道“视在功率等于电压相量乘以电流相量的共轭”。记得上课时,教授给出他的证明过程,我疑惑不已,以为他在凑答案。估计很多人讲不清楚其中的原因。
证明:视在功率等于电压相量乘以电流相量的共轭
已知:电压相量为(U, α), 复阻抗为M[cos(φ)+jsin(φ)]
经过计算:电流初相角为β=(α-φ),I=U/M,得到φ=α-β
根据视在功率等于电压相量的平方除法以复阻抗,得到:
[U*cos(α)+jU*sin(α)] * [U*cos(α)+jU*sin(α)] / M*cos(φ)+jM*sin(φ)]
=U*U*[cos(2α)+ jsin(2α)] / [M*cos(φ)+jM*sin(φ)]
=(U*U/M)* [cos(2α)+ jsin(2α)]* [cos(φ) - jsin(φ)]
=(U*U/M)* [cos(2α)+ jsin(2α)] * [cos(-φ) + jsin(-φ)]
=(U*U/M)* [cos(2α-φ)+ jsin(2α-φ)]
=(U*I)* {cos[2α-(α-β)]+ jsin[2α-(α-β)]}
=(U*I)* [cos(α-β)+ jsin(α-β)]
实部为UIcos(α-β),表示有功功率,虚部为UI sin(α-β),表示无功功率。
因此,视在功率等于电压相量乘以电流相量的共轭。
基尔霍夫第一定律又称基尔霍夫电流定律,简记为KCL,其物理背景是电荷守恒公理。假设进入某节点的电流为正值,离开这节点的电流为负值,则所有涉及这节点的电流的代数和等于零,因此又称为节点电流定律。
基尔霍夫第二定律又称基尔霍夫电压定律,简记为KVL,其物理背景是能量守恒。沿着闭合回路所有元件两端的电势差(电压)的代数和等于零,因此又称为回路电压定律。
相关文章:

相量的加减乘除计算
相量的加减乘除计算 矢量是物理学中的术语,是指具有大小(magnitude)和方向的量。如速度、加速度、力等等就是这样的量。向量是数学中的术语,也称为欧几里得向量、几何向量、矢量。与向量对应的量叫做数量,在物理学中称…...

JavaScript 代码整洁之道
文章目录 概述篇变量篇函数篇注释篇异常处理篇复杂判断函数篇重构篇代码风格常量大写先声明后调用注释 参考资料 概述篇 书写能让人读懂的代码使用英语编写代码团队协作 制定通用的规则,依靠工具让团队的代码风格保持统一,要让代码看起来是由一个人编写…...
socket 及 字节序转换(嵌入式学习)
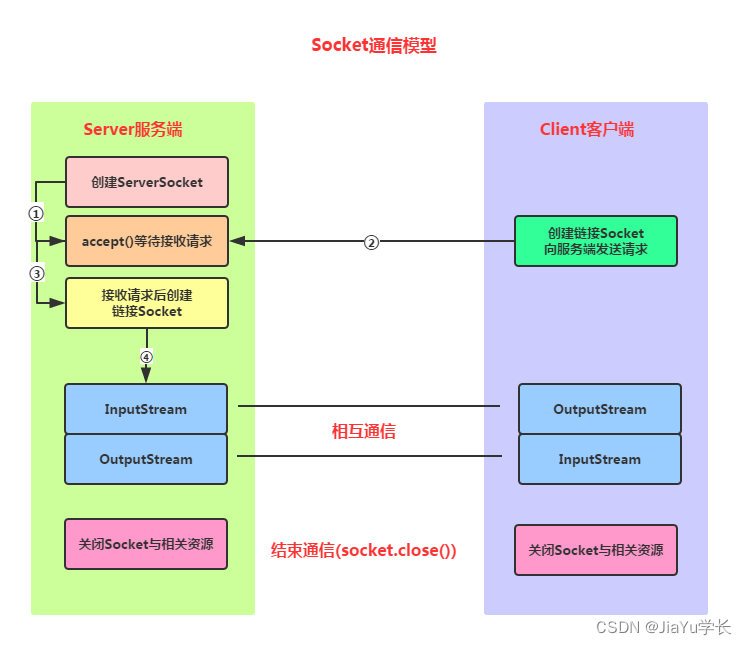
socket 及 字节序转换 socket简介Socket为什么需要Socket?socket类型Socket通信模型 字节序主机字节序到网络字节序网络字节序到主机字节序IP地址转换 socket简介 1、1982 - Berkeley Software Distributions 操作系统引入了socket作为本地进程之间通信的接口 2、1…...
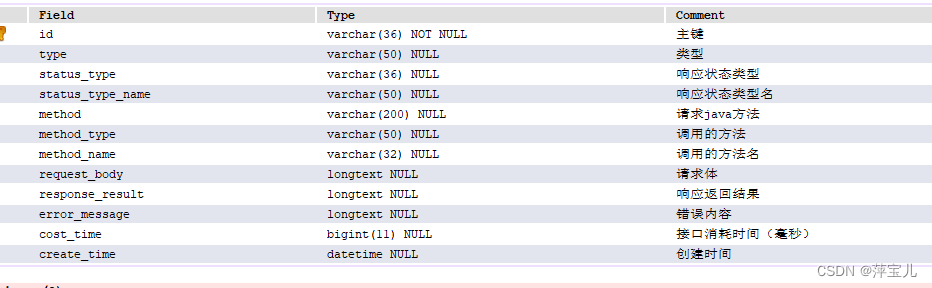
Java之~ Aop自定义注解日志
大纲步骤: 一,创建需要记录的日志表,创建基础方法。(省略) 二,在需要加记录日志的方法上加Aop注解1,创建一个注解类,Aop中定义一个注解import java.lang.annotation.*; /*** http 请…...

编译原理个人作业--第四章
构造FIRST和FOLLOW的大白话网站 第四章 1 考虑文法 G 1 G_1 G1: S → a ∣ ∧ ∣ ( T ) T → T , S ∣ S S \rightarrow a|\land|(T) \\ T\rightarrow T,S|S S→a∣∧∣(T)T→T,S∣S 先复习左递归如何消除 原书p69页 类似于 P → P a ∣ b P\rightarrow Pa|b P→Pa∣b的…...

学习笔记:数据库简介
数据库是一系列可以方便的访问和修改的数据的集合。 所有数据库管理系统的主要工作都是可靠的存储数据并使其对用户可用。 目前最常见的数据库模型主要是两种,即关系型数据库和非关系型数据库。 一、按数据的组织方式 数据从组织的角度上,主要分为结…...
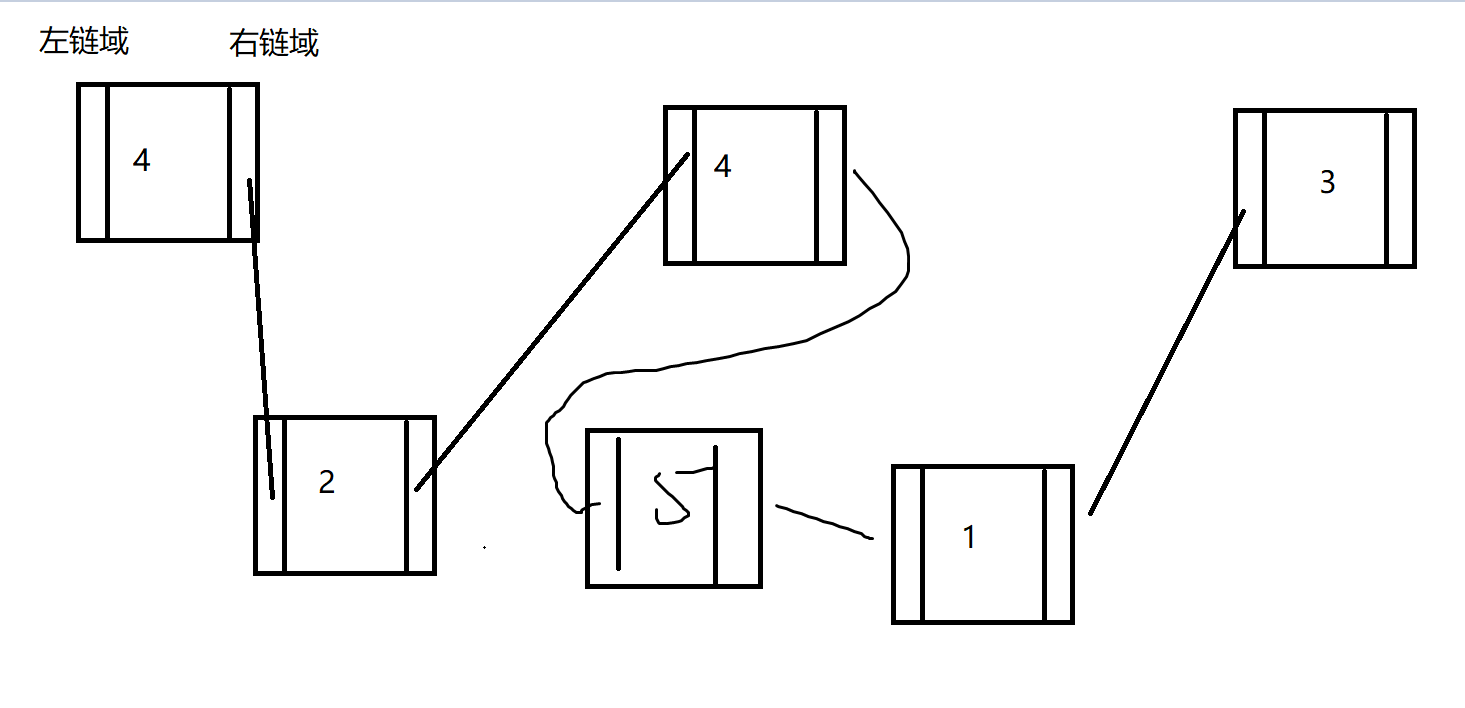
day18_集合
今日内容 零、 复习昨日 一、集合框架体系 二、Collection 三、泛型 四、迭代 五、List 六、ArrayList 七、LinkedList 零、 复习昨日 晨考 一、集合框架体系 数组: 是一个容器,用来存放数据的 定长只能存储同一种数据类型的数据int[] 可以存储int值,Student[] 可以存储引用类型…...

Go面试必会基础题
文章目录 1.下面代码有什么错误?2.下面代码有什么问题?3.下面代码输出什么?4.下面这段代码输出什么? 1.下面代码有什么错误? func main() {one : 0one : 1 }参考答案及解析:变量重复声明。不能在单独的声…...
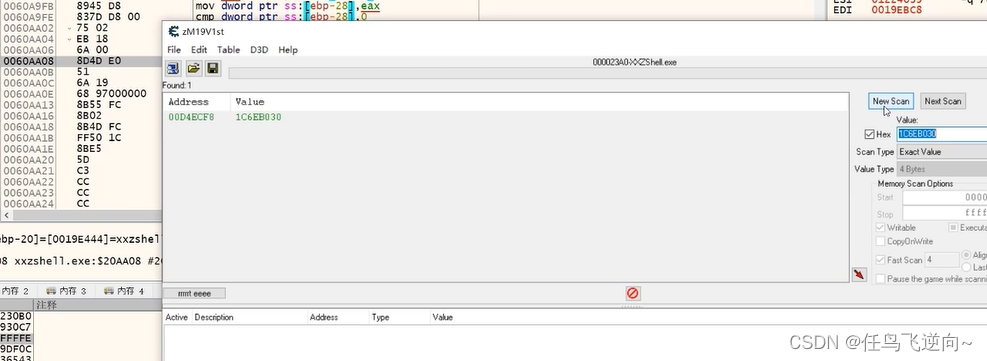
发送封包协议实现XXZ批量秒分解装备
通过发送封包,我们可以让一些反复的枯燥的行为变的简单,高效。 比如XXZ的萃取装备,我们可以一瞬间萃取大量的装备,而省去读条的过程。 我们来萃取一下看看效果 手动萃取是有读条的,那么如果很多装备的话,…...

Spring学习——Nginx
Nginx概述 Nginx介绍 Nginx是一款轻量级的web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器。其特点是占有内存少,并发能力强,事实上nginx的并发能力在同类型的网页服务器中表现较好,中国大陆使用nginx的网…...

记录 vue-cli 安装过程
1. VueCli CLI 是 Commond-Line Interface 的缩写 如果开发大型项目,肯定需要考虑代码目录结构、项目结构和部署、热加载、代码单元测试等事情,那么你必然需要使用 VueCLI,使用 VueCLI 可以快速搭建 vue 开发环境以及对应的 webpack 配置。 …...
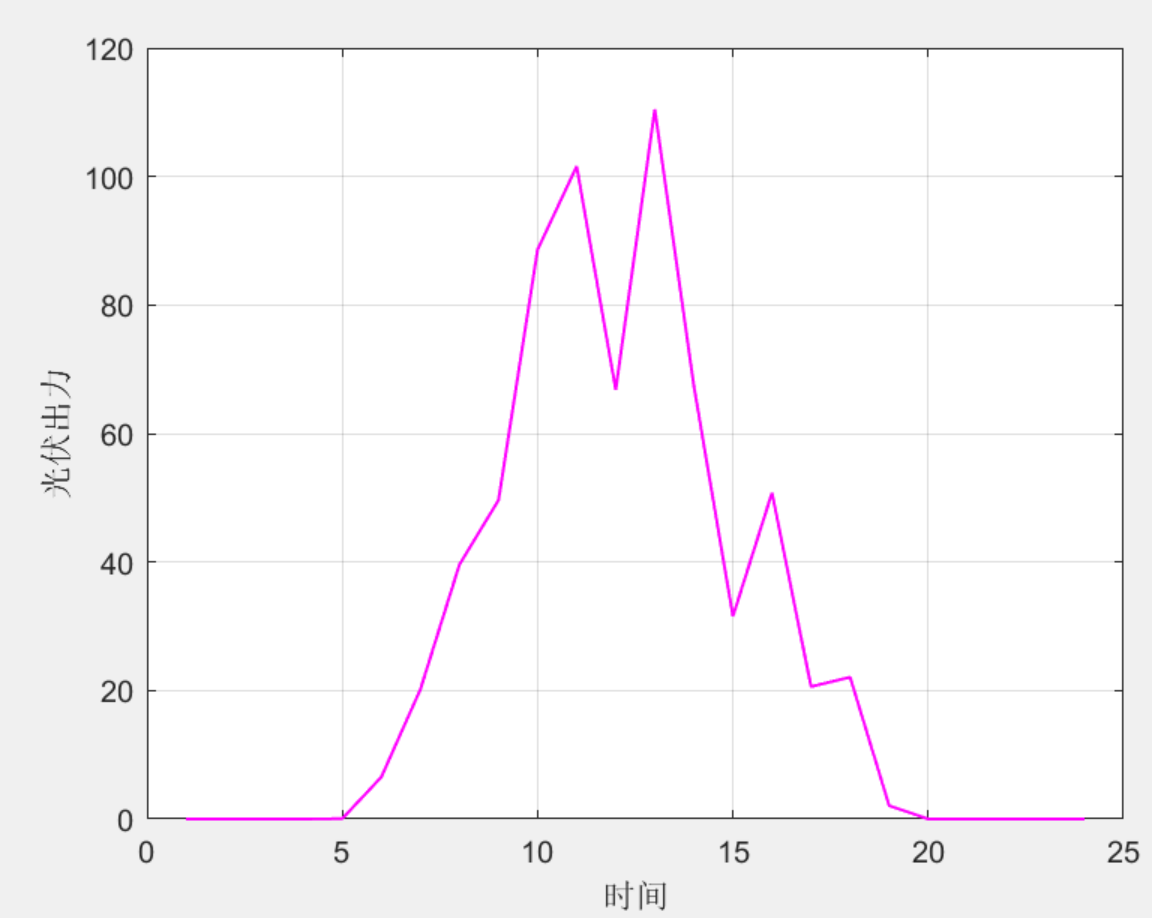
含氢微网优化调度模型matlab
目录 1 主要内容 模型示意图 目标函数 2 部分程序 3 程序结果 4 下载链接 1 主要内容 最近咨询含氢微网优化调度模型的同学较多,本次就分享一个高质量的源码资源。该程序方法复现《Simulation of design and operation of hydrogen energy utilization syste…...

【springcloud开发教程】路由网关——zuul
官方资料:https://github.com/Netflix/zuul/ 什么是Zuul? Zuul包含了两个主要的功能:路由和过滤 路由功能将外部请求转发到具体的微服务实例上,是实现外部访问统一入口的基础,而过滤器功能则负责对请求的处理过程进行干预&#…...

DF竞赛平台携手嬴彻科技与清华大学智能产业研究院,助力自动驾驶挑战赛圆满落幕!
由DataFountain竞赛平台(简称DF平台)提供办赛支持的「首届“嬴彻-清华AIR杯”自动驾驶挑战赛:决策规划算法」已圆满落幕。作为一场前沿性自动驾驶类比赛,本次大赛立足“高速道路”和“城市道路”两大真实场景,选择“半…...
234:vue+openlayers 加载本地shp数据,在map上显示图形
第234个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+openlayers中利用shapefile读取本地的shp数据,并在地图上显示图形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果 文章目录 示例效果安装引用配置方式示例源代码(共143行)相关API参考:专栏…...
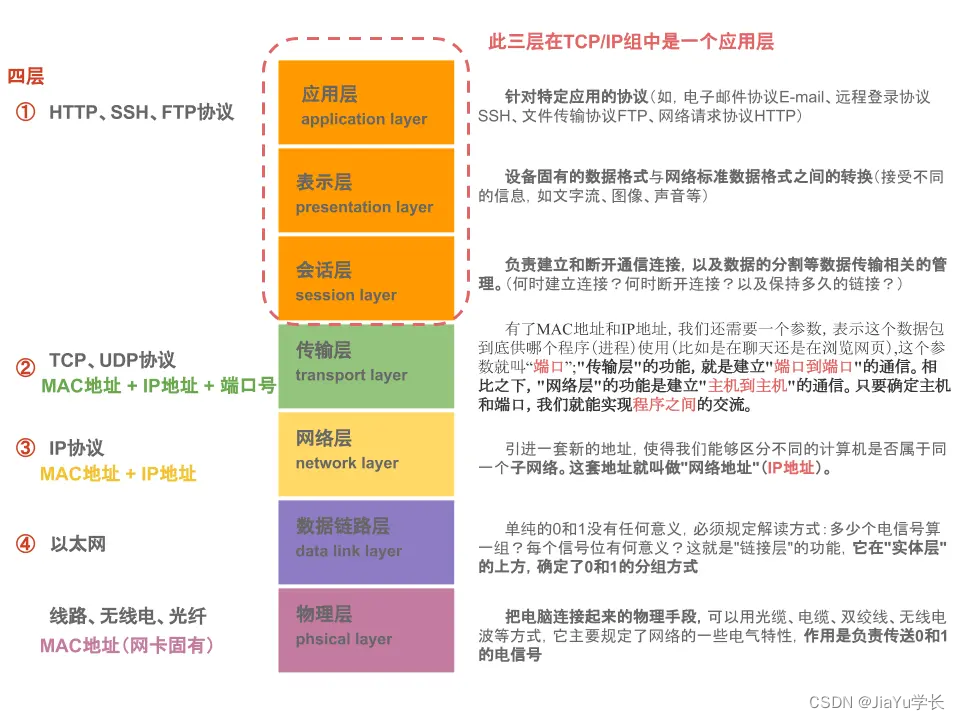
网络模型-网络体系结构(OSI、TCP/IP)
网络模型(网络体系结构) 网络模型网络的体系结构OSI模型TCP/IP模型OSI和TCP/IP模型对应关系图 常见网络协议 网络模型 网络的体系结构 1、网络采用分而治之的方法设计,将网络的功能划分为不同的模块,以分层的形式有机组合在一起…...

园区智慧导览地图软件,智慧工厂导航定位怎么解决方案的
智慧工厂导航定位怎么解决方案的地图新基建是行业的核心数字基础需求之一,行业内中已构建了较为完整的城市级地理信息系统。园区管理涉及众多方面,因此园区的智慧信息化建设至关重要,需求越来越广泛。在智慧园区中,基于园区的电子…...

Redis高可用之3种集群方案对比
Redis集群方案使用建议: Redis cluster:除非是1000个节点以上的超大规模集群,优先考虑使用Redis clustercodis:旧项目如果仍在使用codis,可继续使用,但也推荐迁移到Redis clustertwemproxy:不建…...

java 线程唤醒于阻塞的常用方法
1.分类描述 1.sleep() 休眠2.suspend() 暂停和 resume() 继续3.yield() 让步 就是我放弃本次执行,但继续排队,下一次有机会在执行。 4.wait() 和 notify() notifyAll() 注:这两个方法,属于Object类,而不属于Thread…...
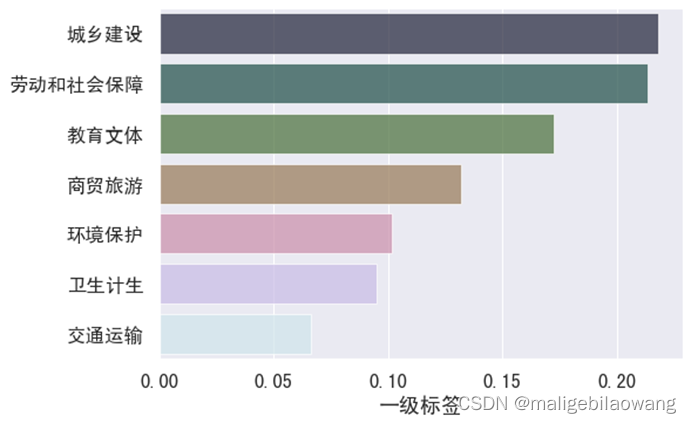
面包多面包多面包多面包多面包多面包多
1.背景 1.摘要 本文是针对智慧政务中的文本数据挖掘应用的研究。通过建立基于三层网络结构的fastText文本分类模型,聚类量化模型,熵权评估模型解决了群众留言分类,热点问题挖掘,答复意见评价等问题。 针对群众留言分类问题&#…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
