回溯算法及其应用
回溯是一种常见的算法思想,用于解决许多优化问题。该算法的核心思想是穷举所有可能的解决方案,然后通过剪枝来减少不必要的计算,以获得最优解。
回溯算法常用于求解组合、排列、子集和等问题。通常情况下,回溯算法需要递归地搜索问题的解空间,并在搜索过程中记录可能的解决方案。如果找到了一个可行的解决方案,则返回该解决方案。如果没有找到解决方案,则回溯并尝试其他可能的解决方案,直到所有可能的解决方案都被尝试过。
以下是一个简单的JavaScript回溯算法示例,用于寻找一个数列中所有可能的子集:
function subsets(nums) {const res = [];const backtrack = (start, path) => {res.push(path.slice());for (let i = start; i < nums.length; i++) {path.push(nums[i]);backtrack(i + 1, path);path.pop();}}backtrack(0, []);return res;
}console.log(subsets([1, 2, 3])); // [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
在此示例中,我们定义了一个backtrack函数来递归搜索解空间。start参数表示在搜索过程中从哪个位置开始搜索,path参数表示当前搜索路径上的所有元素。在每个递归调用中,我们首先将当前路径添加到结果数组res中,然后从start位置开始循环遍历剩余元素,并尝试将其添加到当前路径中。完成搜索后,我们需要回溯并尝试其他可能的解决方案。
接下来,我们来看一个更实际的应用场景:解决数独问题。
数独是一种流行的逻辑游戏,玩家需要在一个九宫格中填入数字,保证每一行、每一列和每一个小九宫格中的数字都不重复。数独问题可以用回溯算法来求解。下面是一个JavaScript实现的示例代码:
function solveSudoku(board) {const ROWS = 9, COLS = 9;const BOXES = [[0, 0], [0, 3], [0, 6],[3, 0], [3, 3], [3, 6],[6, 0], [6, 3], [6, 6]];const isValid = (row, col, num) => {for (let i = 0; i < ROWS; i++) {if (board[i][col] === num) return false;if (board[row][i] === num) return false;}const boxRow = Math.floor(row / 3) * 3;const boxCol = Math.floor(col / 3) * 3;for (let i = boxRow; i < boxRow + 3; i++) {for (let j = boxCol; j < boxCol + 3; j++) {if (board[i][j] === num) return false;}}return true;}const backtrack = (row, col) => {if (col === COLS) {row++;col = 0;}if (row === ROWS) {return true;}if (board[row][col] !== '.') {return backtrack(row, col + 1);}for (let num = 1; num <= 9; num++) {if (isValid(row, col, String(num))) {board[row][col] = String(num);if (backtrack(row, col + 1)) {return true;}board[row][col] = '.';}}return false;}backtrack(0, 0);
}const board = [['5', '3', '.', '.', '7', '.', '.', '.', '.'],['6', '.', '.', '1', '9', '5', '.', '.', '.'],['.', '9', '8', '.', '.', '.', '.', '6', '.'],['8', '.', '.', '.', '6', '.', '.', '.', '3'],['4', '.', '.', '8', '.', '3', '.', '.', '1'],['7', '.', '.', '.', '2', '.', '.', '.', '6'],['.', '6', '.', '.', '.', '.', '2', '8', '.'],['.', '.', '.', '4', '1', '9', '.', '.', '5'],['.', '.', '.', '.', '8', '.', '.', '7', '9']
];solveSudoku(board);console.log(board);
在这个示例代码中,我们首先定义了一些常量和辅助函数。isValid函数用于检查当前位置是否可以填入指定的数字。backtrack函数则是回溯算法的核心,它用于递归地搜索解空间,并在搜索过程中记录可能的解,然后验证这个解是否符合要求。如果符合要求,则继续搜索下一步可能的解;如果不符合要求,则回溯到上一步,重新选择其他可能的解。
在数独问题中,我们从左到右、从上到下依次遍历每一个格子。对于每一个空格,我们依次尝试填入1到9的数字,并检查填入的数字是否合法。如果合法,则继续搜索下一个空格;如果不合法,则回溯到上一个空格重新尝试填入其他数字。
通过回溯算法,我们可以找到数独问题的一个解,如果数独问题有多个解,回溯算法也可以找到所有的解。在这个示例代码中,我们使用了递归的方式实现回溯算法。当找到一个解时,函数返回true,表示已经找到解;当所有可能的解都被尝试过后,函数返回false,表示没有找到解。
回溯算法的时间复杂度一般较高,因为它需要搜索所有可能的解空间。对于数独问题,回溯算法的时间复杂度取决于解的数量,一般来说解的数量不会太多,因此回溯算法是一个有效的求解方法。
总之,回溯算法是一种常用的求解问题的方法,它可以用于求解各种类型的问题,包括数独、八皇后、0/1背包等等。在实际应用中,我们可以结合其他算法和数据结构来优化回溯算法的效率,例如剪枝、记忆化搜索等。
下面是完整的示例代码:
// 数独问题的解决函数
function solveSudoku(board) {// 遍历数独表格for (let i = 0; i < 9; i++) {for (let j = 0; j < 9; j++) {// 如果当前格子为空if (board[i][j] === ".") {// 尝试填入1到9的数字for (let num = 1; num <= 9; num++) {// 如果填入的数字合法if (isValid(board, i, j, num)) {// 填入数字board[i][j] = num.toString();// 递归调用解决函数if (solveSudoku(board)) {// 如果找到解,则返回truereturn true;} else {// 如果没有找到解,则回溯board[i][j] = ".";}}}// 如果尝试了所有的数字都无法得到解,则返回falsereturn false;}}}// 如果遍历完整个数独表格,都没有返回true,则说明已经找到解return true;
}// 检查填入的数字是否合法
function isValid(board, row, col, num) {// 检查行是否合法for (let i = 0; i < 9; i++) {if (board[row][i] === num.toString()) {return false;}}// 检查列是否合法for (let j = 0; j < 9; j++) {if (board[j][col] === num.toString()) {return false;}}// 检查3x3方格是否合法let boxRow = Math.floor(row / 3) * 3;let boxCol = Math.floor(col / 3) * 3;for (let i = boxRow; i < boxRow + 3; i++) {for (let j = boxCol; j < boxCol + 3; j++) {if (board[i][j] === num.toString()) {return false;}}}// 如果行、列、3x3方格都没有重复的数字,则返回truereturn true;
}// 测试代码
let board = [["5", "3", ".", ".", "7", ".", ".", ".", "."],["6", ".", ".", "1", "9", "5", ".", ".", "."],[".", "9", "8", ".", ".", ".", ".", "6", "."],["8", ".", ".", ".", "6", ".", ".", ".", "3"],["4", ".", ".", "8", ".", "3", ".", ".", "1"],["7", ".", ".", ".", "2", ".", ".", ".", "6"],[".", "6", ".", ".", ".", ".", "2", "8", "."],[".", ".", ".", "4", "1", "9", ".", ".", "5"],[".", ".", ".", ".", "8", ".", ".", "7", "9"],
];
if (solveSudoku(board)) {console.log(board);
} else {console.log("No solution");
}
上述代码实现了一个求解数独问题的函数solveSudoku上述代码实现了一个求解数独问题的函数solveSudoku,该函数使用了回溯算法的思想。具体实现过程如下:
- 遍历数独表格的每一个格子,如果当前格子为空,则尝试填入1到9的数字。
- 如果填入的数字合法(即在行、列、3x3方格中都没有重复的数字),则将该数字填入当前格子。
- 递归调用solveSudoku函数,继续填写下一个空格。
- 如果在下一个空格中找到了解,则返回true,表示已经找到解。
- 如果在下一个空格中没有找到解,则回溯到当前格子,将当前格子重新设为".",并尝试填入下一个数字。
- 如果尝试了所有的数字都无法得到解,则返回false。
相关文章:

回溯算法及其应用
回溯是一种常见的算法思想,用于解决许多优化问题。该算法的核心思想是穷举所有可能的解决方案,然后通过剪枝来减少不必要的计算,以获得最优解。 回溯算法常用于求解组合、排列、子集和等问题。通常情况下,回溯算法需要递归地搜索…...

如何一步步打造完美的成绩查询系统平台?
想要搭建一个高效的在线发布成绩查询系统平台,首先需要了解哪些技术和工具是必备的。本文将为您介绍一些主流的技术和工具,帮助您快速搭建一个稳定、安全、易用的成绩查询系统。 想要制作在线成绩查询系统平台有两种方式,第一种是直接使用易…...

P1026 [NOIP2001 提高组] 统计单词个数
题目描述 给出一个长度不超过 200200 的由小写英文字母组成的字母串(该字串以每行 2020 个字母的方式输入,且保证每行一定为 2020 个)。要求将此字母串分成 �k 份,且每份中包含的单词个数加起来总数最大。 每份中包含…...

CTFHub | eval执行
0x00 前言 CTFHub 专注网络安全、信息安全、白帽子技术的在线学习,实训平台。提供优质的赛事及学习服务,拥有完善的题目环境及配套 writeup ,降低 CTF 学习入门门槛,快速帮助选手成长,跟随主流比赛潮流。 0x01 题目描述…...
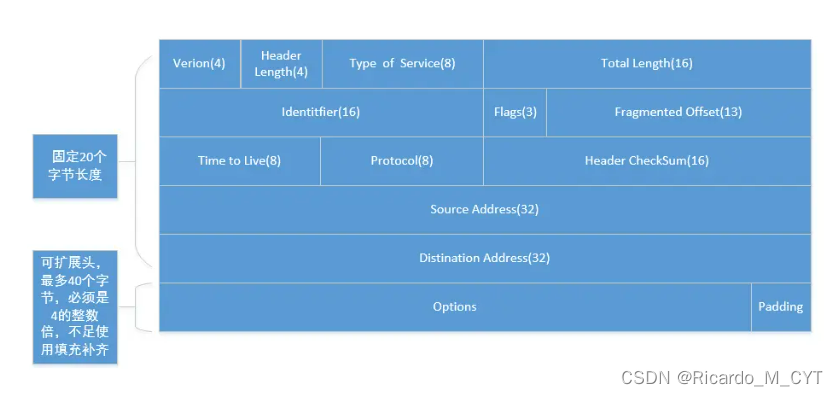
IP协议头
IP 4位版本号(version)4位头部长度(header length)8位服务类型(Type Of Service)16位总长度(total length)16位标识(id)3位标志字段13位分片偏移(…...

【xxl-job定时任务框架详解】
一,分布式任务调度 基本概念 分布式任务调度是一种用于在分布式环境中调度和执行任务的技术。在分布式系统中,由于存在多台服务器、多个进程和线程并行执行,因此需要一种机制来协调和管理任务的执行,避免任务冲突、重复执行、负载不均衡等问题。分布式任务调度通常由一个…...

7、在vscode上利用cmake构建多文件C++工程
文章目录 (1)创建如下工程文件夹:其中头文件放在include文件夹中,源文件放在src文件夹中(2)在vscode上打开工程文件夹,在对应的文件夹内建立相应的文件1)目录结构2)各文件…...

Linux操作系统网络模块
Linux操作系统的网络模块是负责网络通信的核心部分。它通过实现各种协议和算法,使得计算机能够在网络中进行数据交换和通信。网络模块主要包括以下几个方面的功能: (1)IP协议栈:负责处理网络层的数据包,实…...
不同批次板子采集到的传感器压力值不同
问题描述: M340B空压机主控板在接正常压力气源时,显示屏显示压力值过高并报警。 问题排查: 确认可能的故障点:压力传感器、硬件电路(供电电路、分压电路、ADC采样电路等)、单片机、软件; 排…...
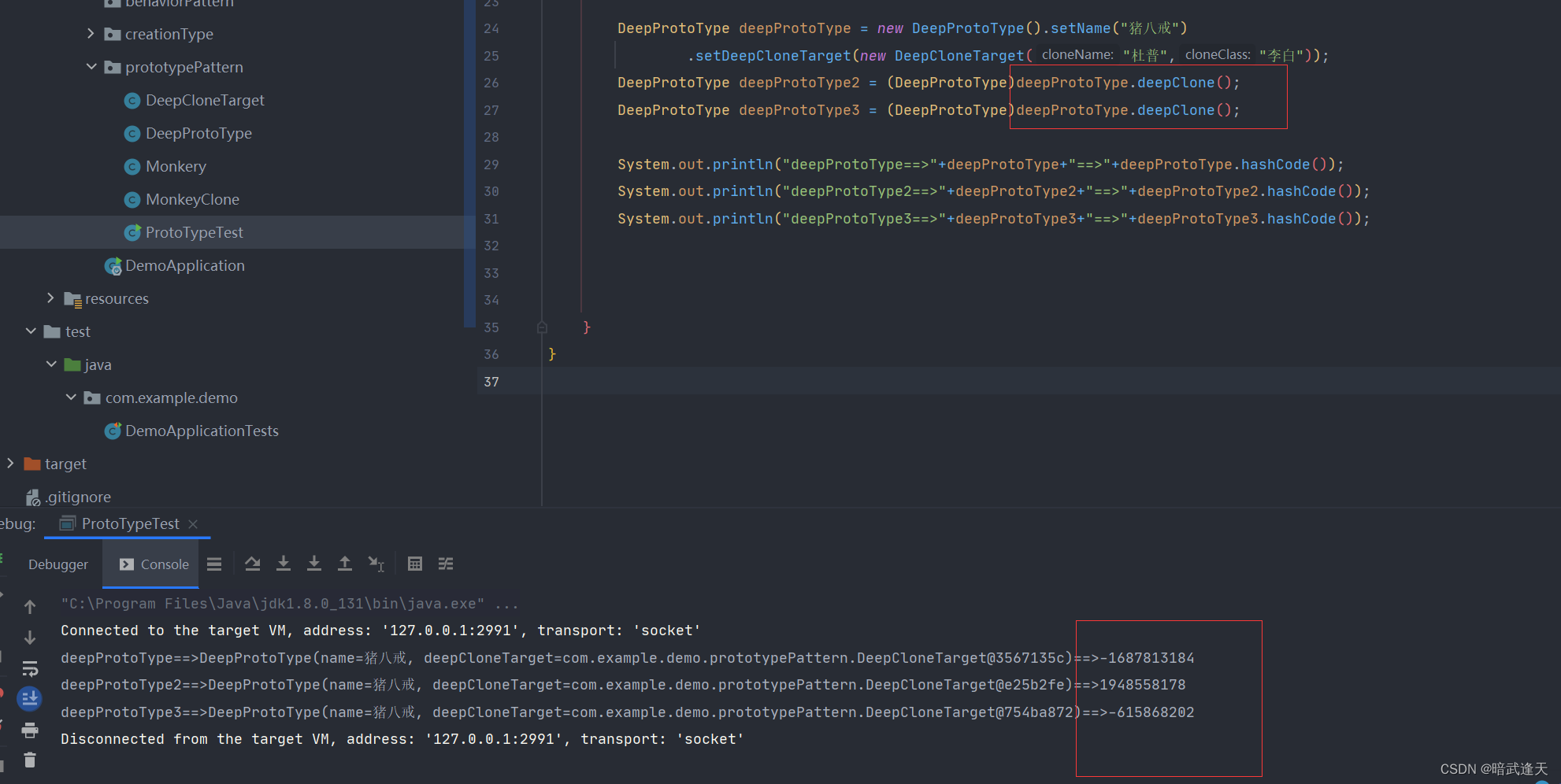
设计模式--原型模式
目录 基本介绍 传统方式克隆 原型模式改进 浅拷贝和深拷贝 浅拷贝的介绍 深拷贝的介绍 原型模式的注意事项和细节 基本介绍 (1) 原型模式(prototype模式): 用原型实例指定创建对象的种类 并且通过拷贝这些原型 创建新的对象 (2) 原型模式是一种创建型设计模式 允许一个…...

C++智能指针shared_ptr详解
智能指针shared_ptr详解 一、简介二、底层原理2.1、引用计数2.2、shared_ptr的构造和析构2.3、shared_ptr的共享和拷贝2.4、循环引用问题 三、shared_ptr的使用3.1、创建一个shared_ptr3.2、共享一个shared_ptr3.3、使用删除器3.4、解除关联 四、使用示例总结 一、简介 C智能指…...

家政服务APP小程序开发功能详解
随着人们生活水平的提高,对家政服务的要求也越来越高。而传统的到家政公司寻找服务人员的方法显然已经无法满足人们需求,取而代之的是线上预约家政服务。家政服务App小程序软件可以满足用户在线预约,还可以根据自己的需求定制家政服务、选择家…...
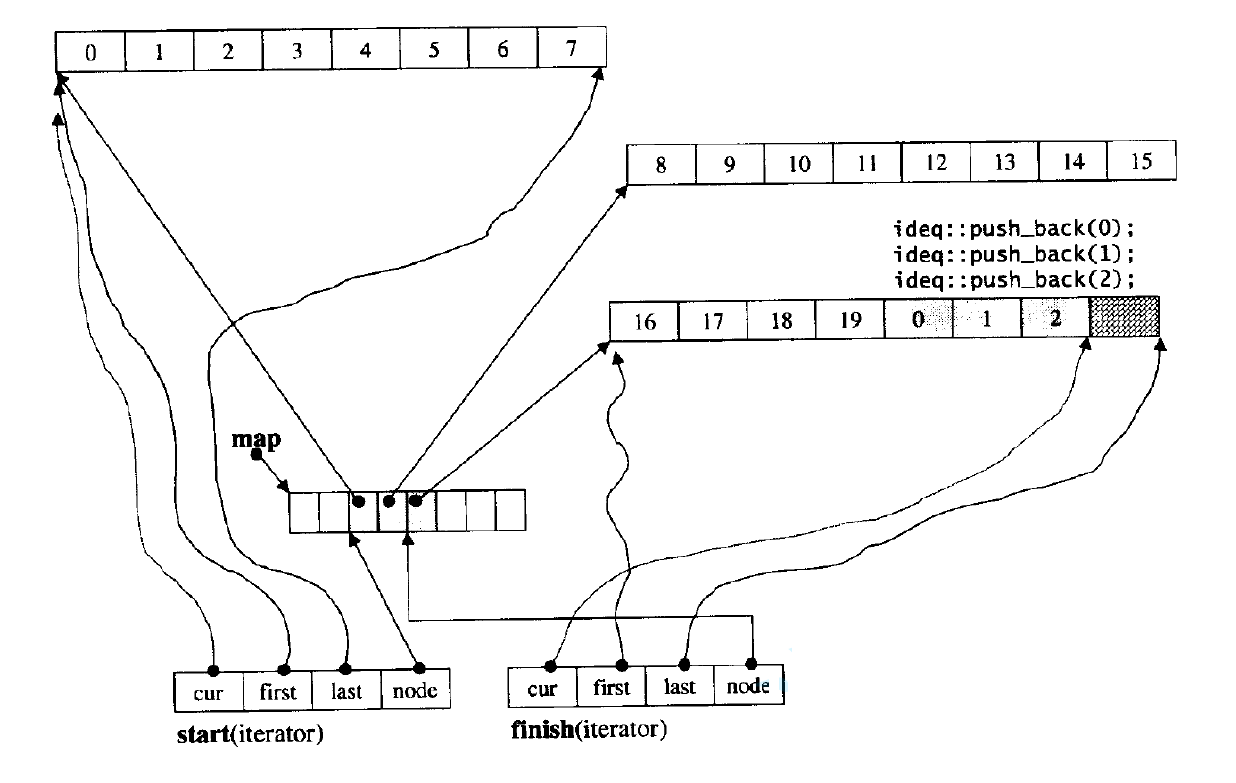
【C++】deque的实现原理简单介绍
前言 deque被称为双端队列,它的出现主要是为了结合vector和list的优点并减小它们的缺点,实际上deque确实结合了vector和list的优点减小了它们的缺点,但是它的结合也让它自己的优点没有原始的vector和list那么极致,导致deque变得很…...

UWB隧道人员定位技术应用,施工作业安全精准保障
隧道施工的安全不仅关系到工程项目的质量和施工效率,也关系到我国的资金安全、施工人员和人民的生命财产安全。如何有效加强隧道施工的安全管理能力,成为隧道施工企业管理者最关心的问题。国家铁道局在《关于加强铁路隧道工程安全工作的若干意见》中指出…...
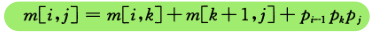
15.2 矩阵链乘法
1.代码 public class MatrixChainMultiplication {public static void main(String[] args) { // 在该代码中,我们首先创建了两个n * n的矩阵m和s,分别用于记录最优值和分割点。 其中m 矩阵 通过i j 来显示在i到j的矩阵链中最优解 // // …...
向隐形冠军学习:聚焦人效,用时间管理提效益
注: 本文来源于盖雅工场联合创始人兼CEO 章新波 在2023狮山论坛“ 向隐形冠军学习: 聚焦人效,用时间管理提效益 ”的主题分享。 文|章新波 整理 |盖雅学苑 在人力资源行业以及各大企业,「人效」这个词…...

Protocol Buffers Go Generated Code Guide
Protocol Buffers Go 代码生成指南 本主题准确描述了协议缓冲区编译器为任何给定的协议定义生成的Go代码。 编译器调用 协议缓冲区编译器需要一个插件来生成Go 代码。使用Go 1.16或更高版本安装,方法是运行: go install google.golang.org/protobuf/…...

Python VTK STL 映射三维模型表面距离
目录 前言: 效果: 实现步骤: Code: 前言: 本文介绍了Python VTK映射三维模型表面距离,通过如何使用VTK计算两个三维模型(stl)的表面距离,并将其距离值以颜色映射到模型,可用于对比 两相模型…...

C# 异常处理机制和常见的异常类型
在 C# 中,异常处理是一个非常重要的概念,它可以让我们在程序发生错误时进行有效的处理,使程序具备更好的鲁棒性。C# 异常处理机制基于 try-catch-finally 语句块,其基本用法如下: try {// 可能会抛出异常的代码 } cat…...

【0187】客户端身份验证配置文件视图之pg_hba_file_rules
文章目录 1. 客户端身份验证配置文件视图2. 视图效果相关阅读: 【0179】配置PostgreSQL以允许远程连接 【0180】PG内核通过pg_hba.conf完成客户端认证(1) 【0181】PG内核通过pg_hba.conf完成客户端认证(2)...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
