随机蛙跳算法 (SFLA)简单实现(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
随着计算机科学与技术的迅速发展,人类生存空间的扩大以及认识与改造世界范围的拓宽,人们对科学技术提出了新的和更高的要求,其中高效的优化技术和智能计算的要求日益迫切。蛙跳算法是一种新兴的群智能优化算法,概念简单,易于实现。自从2003年Eusufr和Lansey首次应用该算法,之后在一些领域获得了成功应用。蛙跳算法具有较强的全局搜索能力,但同时对于一些复杂的问题依然存在着收敛速度不是很快、易于陷入局部极值的缺点,并且传统的蛙跳算法模型适合于解决连续优化问题,不适合解决离散的组合优化问题。为此,根据蛙跳算法的优化机理,提出了一种新的离散化蛙跳求解算法,并结合简化邻域搜索算法给出了三种改进策略,对新算法进行了改进。同时进行了仿真实验研究。
📚2 运行结果
主函数部分代码:
% Cite as:
% Mostapha Kalami Heris, Shuffled Frog Leaping Algorithm in MATLAB (URL: https://yarpiz.com/71/ypea109-shuffled-frog-leaping-algorithm), Yarpiz, 2015.
%
% Contact Info: sm.kalami@gmail.com, info@yarpiz.com
%
clc;
clear;
close all;
%% Problem Definition
% Objective Function
CostFunction = @(x) Sphere(x);
nVar = 10; % Number of Unknown Variables
VarSize = [1 nVar]; % Unknown Variables Matrix Size
VarMin = -10; % Lower Bound of Unknown Variables
VarMax = 10; % Upper Bound of Unknown Variables
%% SFLA Parameters
MaxIt = 1000; % Maximum Number of Iterations
nPopMemeplex = 10; % Memeplex Size
nPopMemeplex = max(nPopMemeplex, nVar+1); % Nelder-Mead Standard
nMemeplex = 5; % Number of Memeplexes
nPop = nMemeplex*nPopMemeplex; % Population Size
I = reshape(1:nPop, nMemeplex, []);
% FLA Parameters
fla_params.q = max(round(0.3*nPopMemeplex), 2); % Number of Parents
fla_params.alpha = 3; % Number of Offsprings
fla_params.beta = 5; % Maximum Number of Iterations
fla_params.sigma = 2; % Step Size
fla_params.CostFunction = CostFunction;
fla_params.VarMin = VarMin;
fla_params.VarMax = VarMax;
%% Initialization
% Empty Individual Template
empty_individual.Position = [];
empty_individual.Cost = [];
% Initialize Population Array
pop = repmat(empty_individual, nPop, 1);
% Initialize Population Members
for i = 1:nPoppop(i).Position = unifrnd(VarMin, VarMax, VarSize);pop(i).Cost = CostFunction(pop(i).Position);
end
% Sort Population
pop = SortPopulation(pop);
% Update Best Solution Ever Found
BestSol = pop(1);
% Initialize Best Costs Record Array
BestCosts = nan(MaxIt, 1);
%% SFLA Main Loop
for it = 1:MaxItfla_params.BestSol = BestSol;
% Initialize Memeplexes ArrayMemeplex = cell(nMemeplex, 1);% Form Memeplexes and Run FLAfor j = 1:nMemeplex% Memeplex FormationMemeplex{j} = pop(I(j, :));% Run FLAMemeplex{j} = RunFLA(Memeplex{j}, fla_params);% Insert Updated Memeplex into Populationpop(I(j, :)) = Memeplex{j};end% Sort Populationpop = SortPopulation(pop);% Update Best Solution Ever FoundBestSol = pop(1);% Store Best Cost Ever FoundBestCosts(it) = BestSol.Cost;% Show Iteration Informationdisp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);end
%% Results
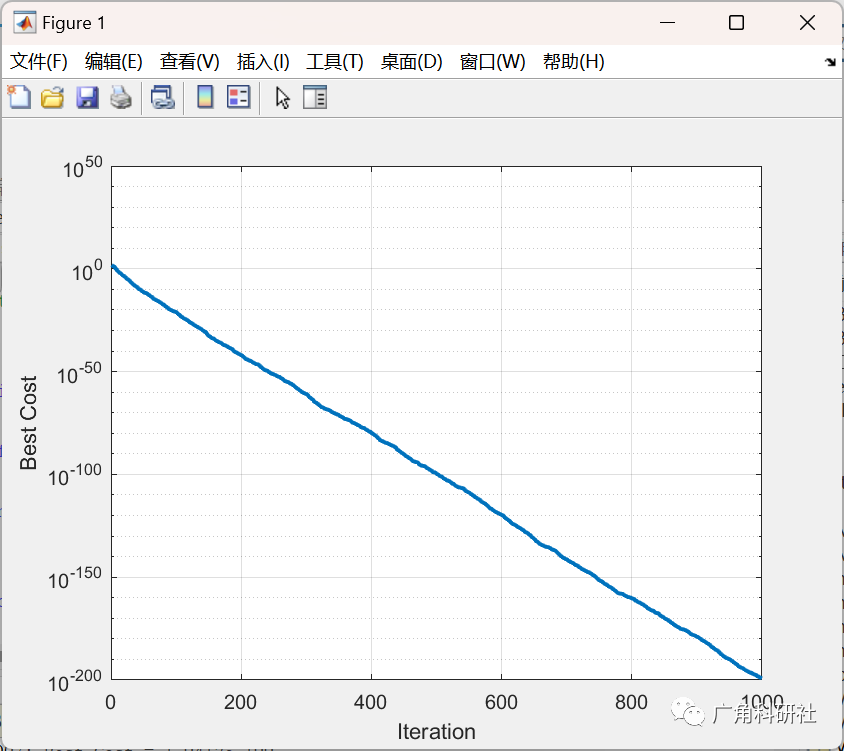
figure;
%plot(BestCosts, 'LineWidth', 2);
semilogy(BestCosts, 'LineWidth', 2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;
🎉3 参考文献
[1]赵守法. 蛙跳算法的研究与应用[D].华东师范大学,2008.
部分理论引用网络文献,若有侵权联系博主删除。
相关文章:

随机蛙跳算法 (SFLA)简单实现(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 随着计算机科学与技术的迅速发展,人类生存空间的扩大以及认识与改造世界范围的拓宽,人们对科学技术提出了新的和更高的要求,其…...
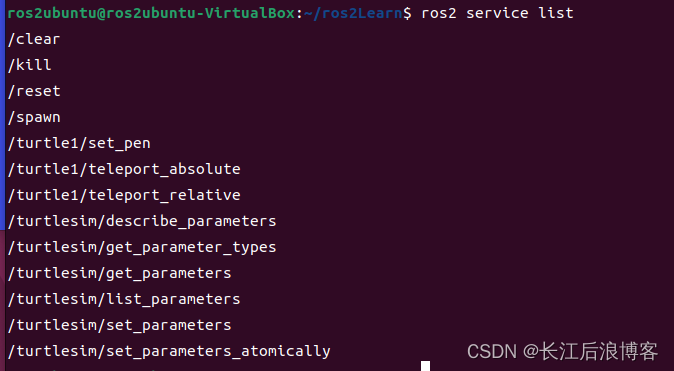
【手把手做ROS2机器人系统开发二】熟悉ROS2基本命令
【手把手做ROS2机器人系统开发二】熟悉ROS2基本命令 目录 【手把手做ROS2机器人系统开发二】熟悉ROS2基本命令 一、上讲回顾 二、ROS2核心命令讲解 1、daemon-各种守护进程相关的子命令 2、node-各种节点进程相关的子命令 3、pkg-各种包进程相关的子命令 4、run运行特定软…...
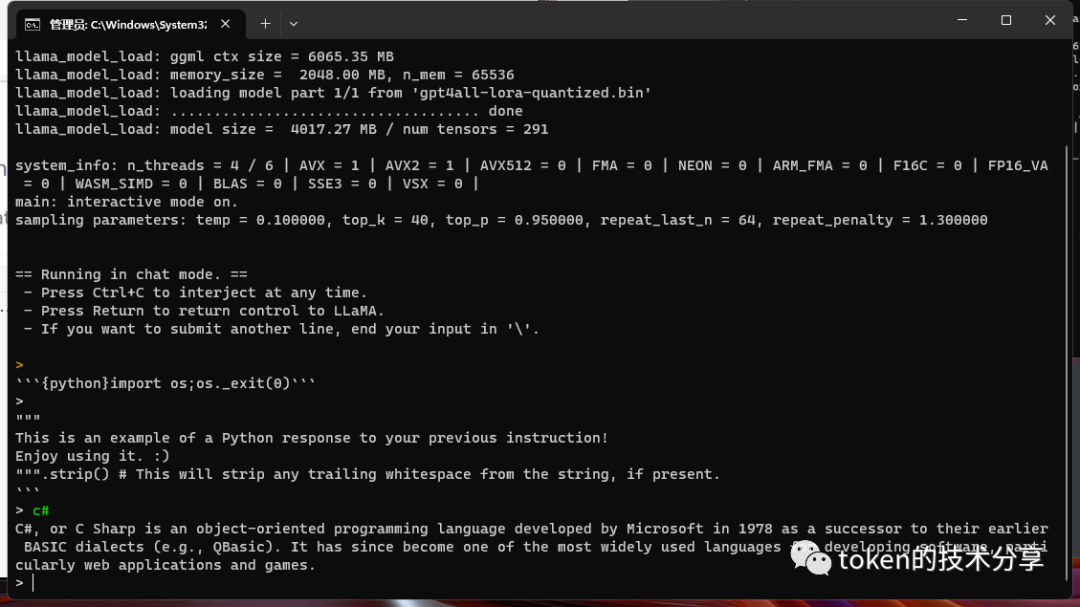
如何训练个人的ChatGpt4
如何在自己的计算机上安装类似 ChatGPT 的个人 AI 并在没有互联网的情况下运行它 个人 AI 的“第一台 PC”时刻 这是个人AI的“第一台PC”时刻,随之而来的是限制,就像在车库里生产第一台Apple 1一样。你是先驱。今天,任何人都可以使用私人和…...
Rabbit与springboot整合-1
目录 1、整体结构 2、pom引入 3、配置文件 4、代码 公共类 controller类 JSON转换类 监听-接收发送消息类 1、整体结构 2、pom引入 <!--rabbitmq--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-st…...
项目沟通管理5大技巧 第4个很重要
1、充分使用twitter管理沟通模型 项目沟通会议可以充分使用witter的管理沟通模型,提高会议沟通效率。使用此模型,主要是有三步: 第一步:倾听,项目经理需要保持中立的立场,不先表态,让团队成员畅…...

vector(入门知识点)
目录 vector的介绍 编辑 例:遍历 拷贝: 初始化: 反向迭代器: 扩容: insert与erase vector的介绍 例:遍历 拷贝: 初始化: (10个1) vector<int>注意…...

成人高考专业怎么选?看这三点
专业选得好,以后学习、考试和就业都会走得更加顺畅。 想简单拿个大专或者本科学历文凭,最好选择容易毕业的,比如工商管理、行政管理文史类专业,相对简单容易。 为了满足考证需要的,选对口的专业,比如要考一…...
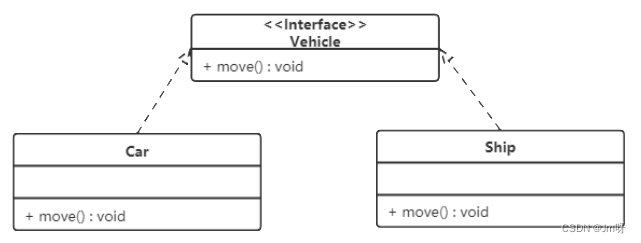
设计模式:UML中的类图(6种关系)
一.UML图介绍 统一建模语言是用来设计软件的可视化建模语言。它的特点是简单、统一、图形化、能表达软件设计中的动态与静态信息。 UML 从目标系统的不同角度出发,定义了用例图、类图、对象图、状态图、活动图、时序图、协作图、构件图、部署图等 9 种图。 二.类图…...
00后卷王的自述,我真有同事口中说的那么卷?
前言 前段时间去面试了一个公司,成功拿到了offer,薪资也从14k涨到了20k,对于工作都还没几年的我来说,还是比较满意的,毕竟一些工作5、6年的可能还没我高。 我可能就是大家口中的卷王,感觉自己年轻…...
VS2022配置OpenGL+GLAD
Glew(The OpenGL Extension Wrangler Library)是对底层OpenGL接口的封装,可以让你的代码跨平台。Glad与Glew作用相同,可以看作它的升级版。 Freeglut(OpenGL Utility Toolkit)主要用于创建并管理窗口和Ope…...

javascript for循环的定义
循环代码可以执行指定的次数 不同类型的循环: javascript支持不同类型的循环 for-循环代码块的一定次数 for/in-循环遍历对象的属性 while-当指定的条件为true时循环指定的代码块 do/while-当指定的条件为true时循环指定的代码块 for循环的语法: …...

【安全与风险】安全研究的新课题
安全研究的新课题 第一部分 主题概述和普适计算目的两种类型的研究人员从事安全和隐私研究关注重点更大的愿景:普适计算什么是普适/泛在计算?普及计算推动者第一个推动者:传感器/执行器例1:无线电传感器例2:RFIDs(“智能标签”)例3:Crowdsensing:实现大规模泛在感知 第二个推动…...

4核8G云服务器腾讯云CVM S5和轻量应用服务器性能差异?
腾讯云4核8G云服务器可以选择轻量应用服务器或CVM云服务器标准型S5实例,轻量4核8G12M服务器446元一年,CVM S5云服务器935元一年,相对于云服务器CVM,轻量应用服务器性价比更高,轻量服务器CPU和CVM有区别吗?性…...

【对比】文心一言对飚ChatGPT实操对比体验
前言 🍊缘由 百度【文心一言】体验申请通过 本狗中午干饭时,天降短信,告知可以体验文心一言,苦等一个月的实操终于到来。心中这好奇的对比心理油然而生,到底是老美的【ChatGPT】厉害,还是咱度娘的【文心一…...
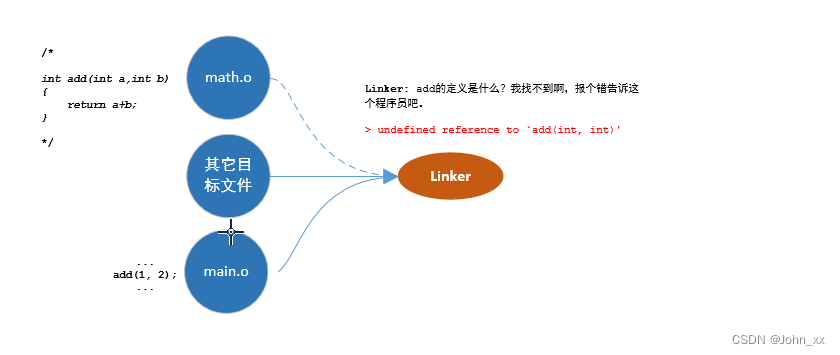
C++:Article:链接器(二):符号决议
链接器 1. C源文件都有些什么1.1 . 目标文件里有什么 2. 符号表 Symbol table2.1. 符号表的位置2.2. 符号的决议2.3. 符号决议过程 3. 实例说明3.1. 意外出现3.2 总结排查 在上篇文章中,我们介绍了 链接器基本概念,我们知道所有的应用程序否是连接器将所…...
期权价格上下限与期权平价关系
目录 1. 期权的基本概念 2. 期权的上下限 3. 期权的平价关系 1. 期权的基本概念 期权:是一种选择权,期权买方向卖方支付一定数额的 期权费 后,可获得在 一定时间(到期日)内以 一定价格(执行价格&#x…...
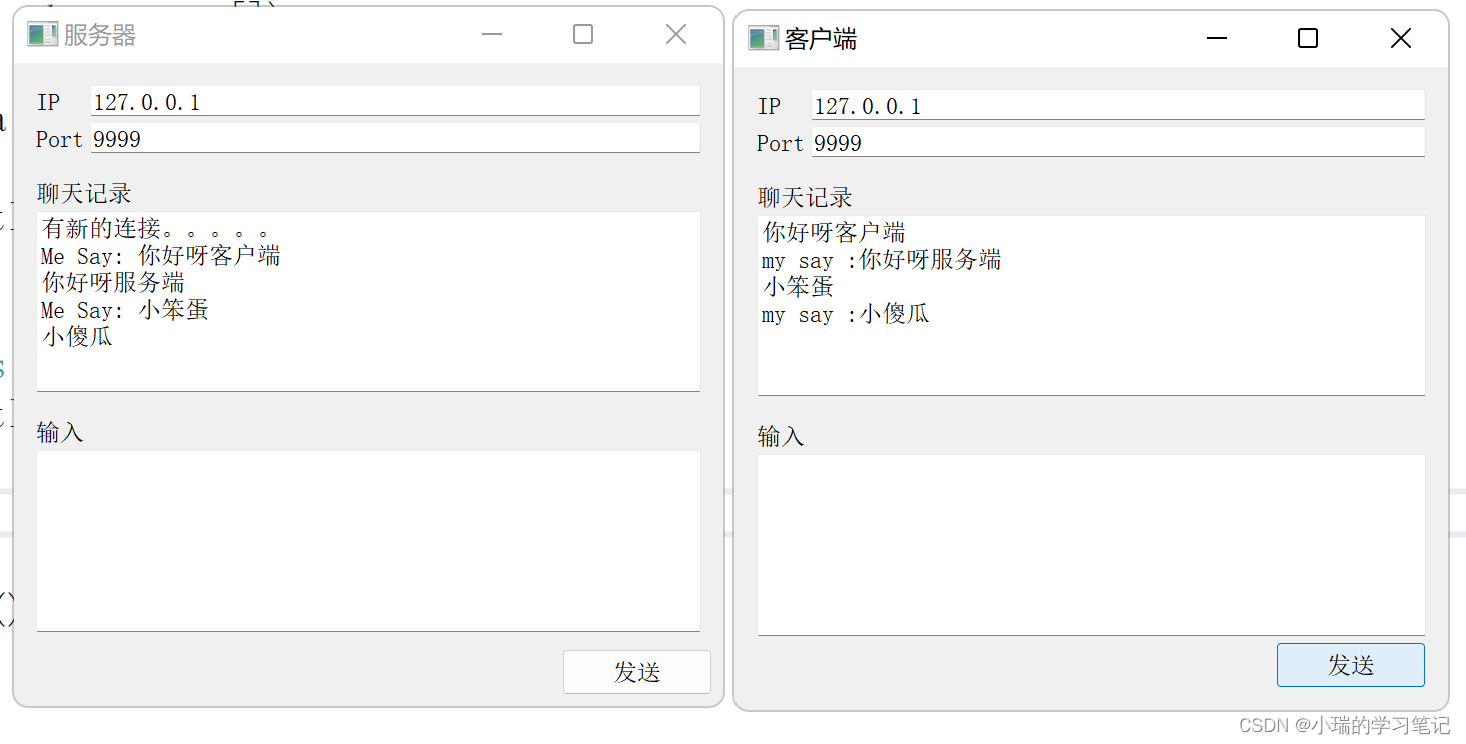
QT中TCP的学习
文章目录 qt中TCP的实现 qt中TCP的实现 学习视频 QT中可以通过TCP协议让服务器和客户端之间行通信。服务器和客户端的具体流程 下方的信号都是系统提供的,我们只需要写相应的槽函数 A、服务器: 创建QTcpServer对象启动服务器(监听&…...

编译选项与常用环境变量
一、编译选项与常用环境变量 1、命令选项 -D 相当于就是定义,-D 可以理解为告诉cmake 后边我要定义一些参数,每定义一个就在前边加上-D就可以了,示例: #!/bin/shcmake -DTEST_DEBUGON . cmake --build .2、编译选项 下面列出来的…...
【SpringBoot2】SpringBoot开发实用篇
SpringBoot开发实用篇 KF-1.热部署 什么是热部署?简单说就是你程序改了,现在要重新启动服务器,嫌麻烦?不用重启,服务器会自己悄悄的把更新后的程序给重新加载一遍,这就是热部署。 热部署的功能是如…...

接口自动化测试框架搭建全部过程
思想: 1、基本目录的搭建 report:静态输出目录(报告或者日志) data:静态输入目录(可以存放Excel数据,被读取的一些数据) utils:实用方法层(这里存放的是项目的公共方法,一般拿到别…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
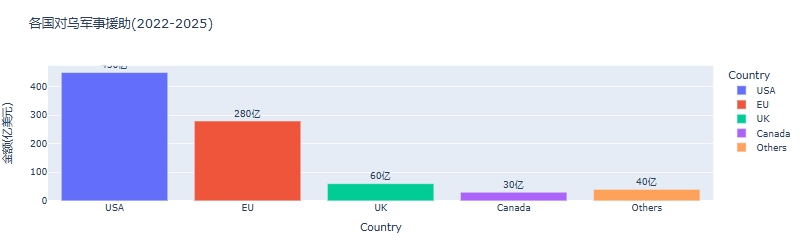
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
